太阳影子定位

张海林 蔡向阳 张卓伟（南京农业大学工学院，江苏南京 210031）

太阳影子定位

张海林 蔡向阳 张卓伟
（南京农业大学工学院，江苏南京 210031）

根据物体太阳影子的变化，可确定视频拍摄的地点和日期。本文通过一些基本的地理公式和解析几何的知识，利用穷举法，最小二乘法思想建立了数学模型，将模型运用于实际数据中得出拍摄地点及日期，附件1的拍摄位置为（109.5°E， 18.3°N），杆长约为2米；附件2的拍摄位置是（79.7° E， 39.5°N），日期是7月20日；拍摄地点的位置是（110.2°E， 29.3°N），日期是1月20日，并检验结果，得出可靠性结论。

影子 穷举 拍摄地点 拍摄日期

1 模型假设

（1）假设光线是完全的直线传播，忽略大气对阳光的折射。

（2）为了忽略坡度的影响，假设本题中的所有测量点都是在水平面上。

2 模型的分析、建立与求解

2.1 问题一模型的分析、建立与求解

问题一要求在综合分析影子的形成原理和变化规律的基础上，利用解析几何的知识，得出影长变化模型；并将公式应用于实际，得出具体的影长变化曲线。

2.1.1 关于影长变化规律的分析与模型的建立

若地面水平，设太阳光线与地面的夹角 ∠ POP'为太阳高度角h，则可得影长与太阳高度角的关系：

时角公式：

太阳高度角公式：

太阳方位角公式：

赤纬角公式

将（3），（7）和（8）联立得影长的计算模型：

2.1.2 模型的实际应用

考虑到天安门位置与东经120（即北京经度）的时间差，利用时差公式：

可得天安门广场的实际时间是8：45：30-14：45：30。以8：45：30为零点，每分钟为一个计量单位在matlab中画图得到影长随时间的变化图如图一所示。

2.2 问题二模型的分析、建立与求解

问题二可分为：（1）建立可确定直杆所处地点的模型；（2）模型的实际应用。

2.2.1 建立可确定直杆所处地点的模型

影子的长度L为：

考虑物体位置与东经120（即北京经度）的时间差，重新定义了时差的计算公式：

T表示物体所处位置的地方时。

结合公式（14），（8），（12）；可得L的关系式： L = φ（H，φ，d，Lo） （15）

其中，Lo表示经度（东经为正，西经为负），W表示纬度（北纬为正，南纬为负）。d表示日期（年，月，日），H表示杆的实长。

利用穷举法，最小二乘法的思想，可得相应的杆长和经纬度。

穷举的目标函数是由公式（12）和公式（15）在同一时刻算出的影长偏差量绝对值的总和最小：min ∑ ΔL，约束条件：（1）Δ L是所给影长 L'和穷举影长的差值；（2）L是关于固定直杆顶点在水平地面上影子坐标的函数；（3）L'是穷举法给出的杆长，纬度，经度以及测量日期的函数。

根据目标函数和约束条件可得数学模型：

2.2.2 模型的实际应用

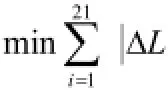
2.2.3 结果的检验

将附件1中部分经度、纬度、杆长和拍摄日期代入2.1.1中的公式（10）：可得此时刻段该地区的杆的影长轨迹图和影长分布图（模型计算曲线），与附件1中给出的影长的变化曲线进行对比（已知数据曲线），对比图如图二所示。

由上图可以看出两条曲线基本重合，故可认为我们所得出的结果较为准确。

2.3 问题三的分析、模型的建立与求解

问题三要求在直杆顶点影子坐标数据已知的情况下，建立数学模型确定直杆所处的地点和日期。并确定附件2和附件3的拍摄地点和拍摄日期。

2.3.1 模型的建立

在本题中可以得出影长L，而经度、纬度、日期和杆的实长都是未知量。因此，采用穷举的方式，具体模型与2.2.1中的模型相似：

2.3.2 模型的实际应用

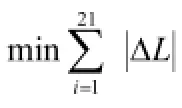
（2）附件2模型结果的检验。利用MATLAB，得到该时刻段该地区的杆的影长轨迹图和影长分布图（蓝线模型计算曲线），与附件2中给出的影长的变化曲线进行对比（已知数据曲线），对比图如图三所示。

由该验证图，我们可以看出通过模型计算出数据的拟合曲线与已知数据的拟合曲线并没有完全重合，但相差最大的地方仅有不到5cm，所以这样的结果也是可以接受的。

附件3求解与附件2类似，这里不在赘述。

［1］吉林省建筑设计院.建筑日照设计［M］.北京:中国建筑工业出版社，1979.

［2］郑鹏飞，林大钧，刘小羊，吴志庭.基于影子轨迹线反求采光效果的技术研究［J］.华东理工大学学报（自然科学版），2010（03）:458-463.

［3］武琳.基于太阳阴影轨迹的经纬度估计技术研究［D］.天津大学，2010.

［4］张宏艺，刘敬民.俯仰角大气折射误差修正方法［J］.光电技术应用，2008（04）:25-27.