切换思维和方法,灵活突围
2016-08-20丁虎平
丁虎平
切换思维和方法,灵活突围
丁虎平
在近几年中考命题中,“统计与概率”涉及的问题背景不断翻新,命题者用智慧设计出一道道亮丽的风景,因此我们的思维也要紧紧跟上.
一、巧用零头,化繁为简
在求平均数和方差时,如果数据较大,计算会很繁琐,我们可以设法将较大的数化为较小的数,简化运算.
1.巧用零头,计算平均数
例1(2015·温州)某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:

笔试 面试 体能甲83 79 90 乙85 80 75 丙80 90 73
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分,根据规定,请你说明谁被录用.

【巧思妙解】(1)选80分作为“基准”,分别计算各项成绩与80的差,得到每一项成绩的“零头”,计算这些“零头”的平均数再加上80即可.

∴84>81>80,
∴排名顺序为甲、丙、乙.
(2)将第(1)小题中得到的“零头”利用加权平均数的计算公式进行计算,再加上80即可.
由题意可知,甲不符合规定.
∴82.5>82.3,
∴录用乙.
【解法说明】这种解法利用了平均数的性质:若一组数据“x1,x2,x3,…,xn”的平均数为,则另一组数据“x1+m,x2+m,x3+m,…,xn+m”的平均数为+m.用这个性质在求算术平均数和加权平均数时可以化大为小,化繁为简,事半功倍.
2.巧用零头,计算方差
例2(2015·镇江)某商场统计了2015 年1~5月A、B两种品牌的冰箱的销售情况,并将获得的数据绘制成折线.
(1)分别求该商场这段时间内A、B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.

【常规思路】(1)从图中读取数据,然后排序求出中位数,直接利用方差的计算公式计算方差;
(2)根据方差的大小判断稳定性.
【巧思妙解】选取一个数据作为基准,用每一个数据减去这个基准,然后再利用方差的计算公式进行计算.
(1)由图可知:A种品牌1~5月的销量分别为:15,17,16,13,14,按照从小到大的顺序排列得到:13,14,15,16,17;B种品牌1~5月的销量分别为:10,14,15,16,20,
∴该商场这段时间内A、B两种品牌冰箱月销售量的中位数分别为15台、15台.
下面计算方差:
A种品牌1~5月的销量分别为:15,17,16,13,14,选13作为基准,用每个月的销量减去13得到一组新的数据:2,4,3,0,1,

B种品牌1~5月的销量分别为:10,14,15,16,20,选取15作为基准,用每个月的销量减去15得到一组新的数据:-5,-1,0,1,5,

∴该商场1~5月A种品牌冰箱月销售量较稳定.
【解法说明】方差实质是各个数据相对于平均数的波动程度,根据方差的性质可知:设一组数据x1,x2,x3,…,xn的平均数是,则方差为;而另一组数据x1+m,x2+m,x3+m,…,xn+m的平均数为+m,此时相应的方差s′2=,因此对于一组较大的数据,我们可以选取一个适当的数作为基准,然后用每一个数据减去这个基准得到一组新的较小的数据,然后计算这一组新数据的方差即可.此外,也可以直接算出一组数据的平均数,然后将每一个数据减去这个平均数得到一组新的较小的数据,然后计算这一组新数据的方差也可以达到同样的目的,
总之,利用转化的数学思想,将较大的数转化为较小的数,巧用“零头”,简化运算.
二、另辟蹊径,巧解概率题
在初中数学中,解决概率问题,常用的方法是画树状图法或列表法,即采用列举的方法列出所有可能的结果,再进行计算.但是有些概率题,我们可以换一种思维方式再辅以列举法,往往能够比较简便地得到答案.下面,结合几道题介绍一些解概率题的巧妙方法.
例3(2014·宁波)如图1,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是().
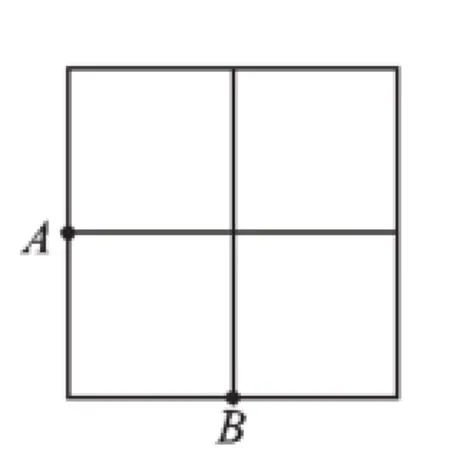
图1

图2
【常规思路】通过列表或画树状图的方法列举出所有的情况.

例4(2014·雅安)若我们把十位上的数字比个位和百位上数字都小的三位数称为“V”数,如756,326,那么从2,3,4这三个数字组成的无重复数字的三位数中任意抽取一个数,则该数是“V”数的概率为______.
【常规思路】通过列表或画树状图的方法列举出所有的情况.

例5(2014·嘉兴)有两辆车按1,2编号,舟舟和嘉嘉两人可任意选坐一辆车.则两人同坐2号车的概率为_________.
【常规思路】通过列表或画树状图的方法列举出所有的情况.

例6小明和小丽做游戏,规则如下:小明转动转盘(转盘被分成二等分,若指针指向分割线则重新转一次),得到一个数字,小丽抛掷一枚质地均匀的骰子一次,得到一个数字,若这两个数字的乘积是奇数,则小明赢,否则小丽赢.问这个游戏公平吗?

【常规思路】通过列表或画树状图的方法列举出所有的情况.
【另辟蹊径】转动转盘,有两个等可能的结果:数字1和2;抛掷骰子有6个等可能的结果:数字1-6.数字1与1-6这六个数字的乘积中有3个奇数3个偶数,数字2与1-6这六个数字的乘积均为偶数,显然不公平.
(作者单位:江苏省镇江市宜城中学)
