针对统计概率题 教你如何得满分

陈锁林　赵志林



针对统计概率题教你如何得满分

陈锁林赵志林

统计与概率部分考题一般难度不大，虽然少数考题能力要求较高，不过分数应该是很容易拿到手的，但我们从近几年中考阅卷发现，这部分题目的得分率并不高，同学们出现的问题主要是：会而不对、对而不全、书写画图不规范、关键步骤缺少、答非所问、不答等，失掉了不该失的分，实在令人惋惜.

那么，面对统计与概率的考题，如何得满分呢？

其实很简单，在中考阅卷时，为了让大家多得分，常采用人性化的给分原则，即在题目所考查的知识点中，每个点都事先给定了分数，你答出几点，就得多少分，反之，你少几点，就会少得分，这种方法叫“分步踩点给分”.下面就以实例说明.

例1（2015·镇江）活动1：在一只不透明的口袋中装有标号为1，2，3的3个小球，这些球除标号外都相同，充分搅匀，甲、乙、丙三位同学以丙→甲→乙的顺序依次从袋中各摸出一个球（不放回），摸到1号球胜出，计算甲胜出的概率.（注：丙→甲→乙表示丙第一个摸球，甲第二个摸球，乙最后一个摸球）

活动2：在一只不透明的口袋中装有标号为1，2，3，4的4个小球，这些球除标号外都相同，充分搅匀，请你对甲、乙、丙三名同学规定一个摸球顺序：_______→_______→_______，他们按这个顺序从袋中各摸出一个球（不放回），摸到1号球胜出，则第一个摸球的同学胜出的概率等于_______，最后一个摸球的同学胜出的概率等于_______.

猜想：在一只不透明的口袋中装有标号为1，2，3，…，n（n为正整数）的n个小球，这些球除标号外都相同，充分搅匀，甲、乙、丙三名同学从袋中各摸出一个球（不放回），摸到1号球胜出，猜想：这三名同学每人胜出的概率之间的大小关系.

你还能得到什么活动经验？（写出一个即可）

【思维切入】（1）画出树状图，通过计算判断出甲胜出的概率是多少即可.

（2）首先对甲、乙、丙三名同学规定一个摸球顺序，在此以丙→甲→乙为例，然后画出树状图，判断出第一个摸球的丙同学和最后一个摸球的乙同学胜出的概率各等于多少即可.

（3）首先根据（1）（2），猜想这三名同学每人胜出的概率之间的大小关系为：P（甲胜出）=P（乙胜出）=P（丙胜出），然后总结出得到的活动经验为：抽签是公平的，与顺序无关.

【解答】（1）如图1，

图1

甲胜出的概率为：

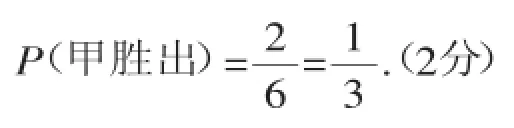
（2）对甲、乙、丙三名同学规定一个摸球顺序：丙→甲→乙，画树状图，如图2，

图2

（3）这三名同学每人胜出的概率之间的大小关系为：P（甲胜出）=P（乙胜出）=P（丙胜出）.

得到的活动经验为：抽签是公平的，与顺序无关.（答案不唯一）（7分）

【踩点得分提示】本题满分为7分.阅卷时，我们把这7分细化到三问，即活动一2分，活动二3分，猜想2分.这道题对同学们的要求还是比较高的，需要大家能从活动一的解答中获得提示，在解决活动二时，先定摸球顺序，再画图、计算、判断，得到正确结论.对于第三问的猜想，不但要求大家对知识有深刻的理解，还要能根据上面两个活动正确猜想，需要有一定的归纳能力、数学论证能力、完整书面表达能力等.答题时，同学们除了要注意解题是否规范、书写是否完整等问题外，还要注意：解题过程中所画的树状图要清晰，活动二的结论要填到题目中的空格内，第三问猜想的结论要精准，对活动经验的总结要简洁明了、符合数学原理.另外，本题选用画树状图法将极大方便问题的解决.

统计类考题一般会出现相关图表，而概率类问题一般需要我们制作图表来分析、解决问题，学会读图、用图、制图就是解决此类问题的钥匙.下面，我们举几个例子来学习如何利用图表来解题.

例2（2015·南京）某工程队有14名员工，他们的工种及相应每人每月工资如下表所示：

工种　人数　每人每月工资/元电工　5　7 000木工　4　6 000瓦工　5　5 000

现该工程队进行了人员调整：减少木工2名，增加电工、瓦工各1名，与调整前相比，该工程队员每月工资的方差_______（填“变小”、“不变”或“变大”）.

【思维切入】从图表中我们发现，人员的变化并没有使平均数发生变化，所以根据方差的概念，我们只要考虑变化前后数据与平均数差值平方的变化情况即可.

【解答】∵减少木工2名，增加电工、瓦工各1名，∴这组数据的平均数不变，但是每个数据减去平均数后平方和增大，则该工程队员每月工资的方差变大.故答案为：变大.

【踩点得分提示】本题考查同学们对平均数和方差概念的理解.在解决本题时，并不需要求出方差的具体数值再进行比较，而是体会方差随整体数据在平均数上下的变化情况.正确解答本题一是读懂表格，用增减法判断出平均数不变；二是通过读表格，发现相对平均数来说，“大”数据（电工）和“小”（瓦工）数据都有所增加，所以离散程度变大，从而方差变大.

例3（2015·鄂州）为了解某社区居民的用电情况，随机对该社区10户居民进行调查，下表是这10户居民2015年4月份用电量的调查结果：

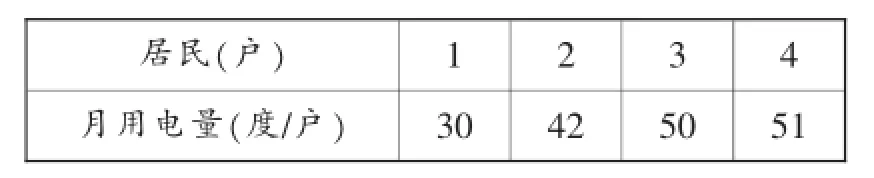
居民（户）　1　2　3　4月用电量（度/户）　30　42　50　51

那么关于这10户居民月用电量（单位：度），下列说法错误的是（）.

A.中位数是50度B.众数是51度

C.平均数是43.5度D.极差是21度

【思维切入】首先是要读懂表格，表格的第一行表示的是用电量为第二行各度数的户数，而不是表示的第几户，接着可以根据统计的有关概念来解决问题.

【解答】共计10户，中位数应是从大到小或从小到大排列的第5户50度和第6户50度的平均数，所以中位数是50度，故A正确；众数是51度，故B正确；极差是21度，故D正确.而平均数应是46.8，故C错误.

【踩点得分提示】本题主要是考查同学们在正确阅读图表的基础上，利用统计概念解决问题，关键是读懂“居民（户）”表示的意义.

例4（2015·孝感）2015年1月，市教育局在全市中小学中选取了63所学校，从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查，了解他们每天在课外用于学习的时间，并绘制成如下不完整的统计图.

根据上述信息，解答下列问题：

（1）本次抽取的学生人数是________，扇形统计图中的圆心角α等于_________，补全统计直方图.

（2）被抽取的学生还要进行一次50米跑测试，每5人一组进行.在随机分组时，小红、小花两名女生被分到同一个小组，请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.

【思维切入】对比直方图和扇形统计图，样本的各组数据是一一对应的，3～4小时这组即是问题的突破口，根据本组人数和占比即可求出样本容量；α的度数可以根据2～3小时这组在样本中的占比求得；小红、小花抽在相邻两道的概率通过列表或者画树状图来求得.

【解答】（1）6÷20%=30，（30-3-7-6-2）÷30×360°=12÷30×360°=144°，扇形统计图中的圆心角α等于144°.

补全统计直方图如图所示：

（2）设竖列为小红抽取的跑道，横排为小花抽取的跑道，根据题意列表如下：

记小红和小花抽在相邻两道这个事件为A，

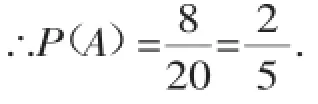
【踩点得分提示】本题考查了列表法和画树状图法求概率，频数分布直方图，扇形统计图.首先要正确地识图，清楚直方图和扇形统计图之间的对应关系，找到问题的突破点是解题的关键.

总而言之，因为考点多、分值分散，失掉1分会严重影响答题的得分率，所以做统计概率题，踩点得分很重要，特别是读图画图时，记住把题中信息在图中标出或画出，把图表中信息写出来，想到多少写多少，这样不但可方便自己解题，特别是万一遇上一个没把握全解出来的问题，还可让阅卷老师从中寻找得分点、踩点给分.

（作者单位：江苏省镇江市宜城中学、江苏省镇江新区教育发展中心）