思路简单易贯通，表达规范不跳步——圆的证明题解答提醒

崔萍



思路简单易贯通，表达规范不跳步
——圆的证明题解答提醒

崔萍

由于“课程标准”对圆的要求有所降低，所以各地中考卷中涉及圆的证明要求进一步下降，如果发现考查圆的相关证明题位于解答题的前5题，这基本上是基础题、送分题，这时同学们往往能“秒杀”思路，接下来要做的就是规范表达几何推理语句，不能随意乱跳步骤，避免“会而不对、对而不全”现象.

例1（2015·盐城）如图1，在△ABC中，∠CAB=90°，∠CBA=50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED=EA.

（1）求∠DOA的度数；

（2）求证：直线ED与⊙O相切.

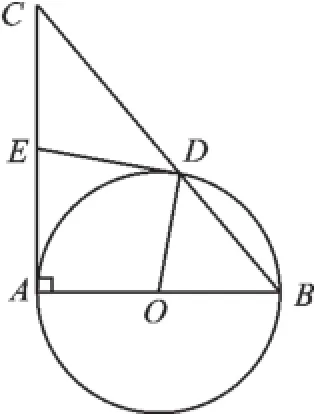
图1

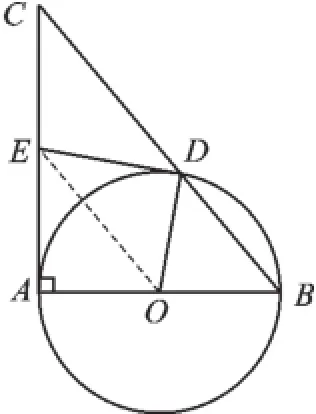
图2

【思路讲解】（1）∠DOA=100°. （2）连接OE，如图2，

∴△EAO≌△EDO（SSS），

∴∠EAO=∠EDO=90°，

∴直线ED与⊙O相切.

【反思回顾】切线的判定与性质是必考知识点，就证明来看，通常都是简单的送分题，这时注意规范证明步骤和几何语句的表达是很关键的，不能随意跳过程.

例2（2015·南京）如图3，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE.

（1）求证：∠A= ∠AEB；

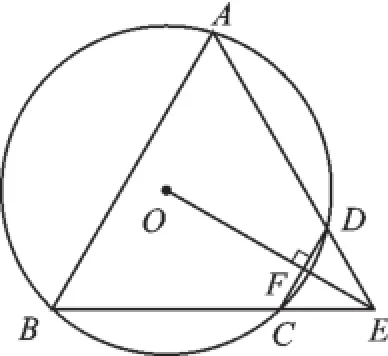
图3

（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形.

【思路讲解】（1）根据圆内接四边形的性质可得∠A+∠BCD=180°，根据邻补角定义可得∠DCE+∠BCD=180°，进而得到∠A=∠DCE，然后利用等边对等角可得∠DCE=∠AEB，进而可得∠A=∠AEB.

（2）首先证明△DCE是等边三角形，进而可得∠AEB=60°，再根据∠A=∠AEB，可得△ABE是等腰三角形，进而可得△ABE是等边三角形.

【规范解答】

证明：（1）∵四边形ABCD是⊙O的内接四边形，

∴∠A+∠BCD=180°，

∵∠DCE+∠BCD=180°，

∴∠A=∠DCE，

∵DC=DE，∴∠DCE=∠AEB，

∴∠A=∠AEB.

（2）∵OE过圆心，EO⊥CD，

∴CF=DF，

∴EO是CD的垂直平分线，

∴ED=EC，

∵DC=DE，∴DC=DE=EC，

∴△DCE是等边三角形，

∴∠AEB=60°，由（1）∠A=∠AEB，

∴△ABE是等边三角形.

【反思回顾】本题主要考查了等边三角形的判定和性质，垂径定理以及圆内接四边形的性质，解题关键是掌握圆内接四边形对角互补，否则无法将各个条件集中到特殊的三角形中（如直角三角形或等边三角形）.

（作者单位：江苏省南通市第一初级中学）