“结伴而行”：一类平行四边形折叠考题

朱海峰



“结伴而行”：一类平行四边形折叠考题

朱海峰

平行四边形与折叠相结合一直是热点考题，检索2015年江苏省13市中考数学卷就不少于5道类似的考题，下面我们选取两例解答题，破解思路，展示解法，并反思回顾.

例1（2015·连云港）如图1，将平行四边形ABCD沿对角线BD进行折叠，折叠后点C落在点F处，DF交AB于点E.

图1

（1）求证：∠EDB=∠EBD；

（2）判断AF与DB是否平行，并说明理由.

【思路讲解】（1）由折叠可得∠CDB= ∠EDB，再由四边形ABCD是平行四边形可得DC∥AB，从而得到∠CDB=∠EBD，问题得证.

（2）先证明AE=EF，得出∠AFE=∠EAF，然后根据三角形内角和定理与等式性质可证明∠BDE=∠AFE，从而得出AF∥BD.

【规范解答】（1）证明：由折叠可知：

∠CDB=∠EDB，

∵四边形ABCD是平行四边形，

∴DC∥AB，∴∠CDB=∠EBD，

∴∠EDB=∠EBD.

（2）AF∥DB.理由如下：

∵∠EDB=∠EBD，∴DE=BE.

由折叠可知：DC=DF，

∵四边形ABCD是平行四边形，

∴DC=AB，∴DF=AB，

∴AE=EF，∴∠EAF=∠EFA.

在△BED中，∠EDB+∠EBD+∠DEB= 180°，∴2∠EDB+∠DEB=180°.

同理，在△AEF中，2∠EFA+∠AEF= 180°.

∵∠DEB=∠AEF，∴∠EDB=∠EFA.

∴AF∥DB.

【反思回顾】这道考题涉及翻折变换（折叠问题）、平行四边形的性质、平行的判定和性质、三角形内角和定理、等腰三角形的判定和性质.这里值得强调的是，在这类问题的解答上有一个规范，即需要先回复“平行”，然后再给出“理由如下”，答题时需要注意，这是一个踩分点.

例2（2015·扬州）如图2，将▱ABCD沿过点A的直线折叠，使点D落到AB边上的点D′处，折痕交CD边于点E，连接BE.

（1）求证：四边形BCED′是平行四边形；

（2）若BE平分∠ABC，求证：AB2=AE2+ BE2.

图2

【思路讲解】

（1）要证四边形BCED′是平行四边形，根据一组对边平行且相等的四边形是平行四边形的判定.一方面，由四边形ABCD是平行四边形可有EC∥D′B；另一方面，由折叠对称的性质、平行线的内错角相等性质、等腰三角形的等角对等边的性质可得EC= D′B，从而得证.

（2）要证AB2=AE2+BE2，根据勾股定理，只要△ABE的∠AEB=90°即可，而要证∠AEB=90°，由BE平分∠ABC可得∠4=∠5（如图3），由ED′∥CB可得∠4=∠6，从而得到∠5=∠6，结合（1）∠2=∠3即可根据三角形内角和定理得到∠AEB=90°，进而得证.

【规范解答】

证明：（1）如图3，

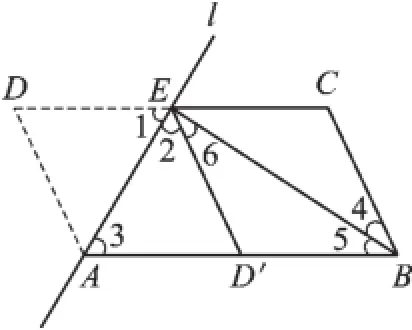
图3

∵将▱ABCD沿过点A的直线AE折叠，

∴DE=D′E，∠1=∠2.

∵四边形ABCD是平行四边形，

∴DC∥AB，∴∠1=∠3，

∴∠2=∠3，∴D′E=AD′，∴DE=AD′.

∵四边形ABCD是平行四边形，

∴DC=AB，∴EC=D′B，∴EC∥D′B，

∴四边形BCED′是平行四边形.

（2）如图3，

∵BE平分∠ABC，∴∠4=∠5.

∵四边形BCED′是平行四边形，

∴ED′∥CB，∴∠4=∠6，∴∠5=∠6.

由（1）∠2=∠3，∴∠2+∠6=∠3+∠5= 90°，即∠AEB=90°，

∴在Rt△ABE中，由勾股定理，得AB2= AE2+BE2.

【反思回顾】这道几何题有效考查了平行四边形的性质、判定，第（2）问综合了轴对称、勾股定理等知识，由于试题难度所限，考查到运用勾股定理为止，作为必要的“成果扩大”，我们还可提出如下问题供同学们继续思考：

（3）请指出四边形BCED′的形状，并说明理由；

（4）求证：在△ABE中，AB边上的中线等于边AB的一半.

（作者单位：江苏省如东县实验中学）