必考题型如何规范解答？——以两道平行四边形证明题为例

吕兵



必考题型如何规范解答？
——以两道平行四边形证明题为例

吕兵

平行四边形是中考必考的题型，常常与全等三角形、特殊三角形结合在一起作为基础题考查，这类基础考题如何做到“会而不错”是十分关键的.下面选取2015年两道中考题讲解思路，给出规范解答，引导回顾，并讲评注意事项.

图1

例1（2015·常州）如图1，在▱ABCD中，∠BCD=120°，分别延长DC、BC到点E，F，使得△BCE和△CDF都是正三角形.

（1）求证：AE=AF；

（2）求∠EAF的度数.

【思路讲解】

（1）由平行四边形的性质得出∠BAD= ∠BCD=120°，∠ABC=∠ADC，AB=CD，BC= AD，由等边三角形的性质得出BE=BC，DF= CD，∠EBC=∠CDF=60°，从而证出∠ABE= ∠FDA，AB=DF，BE=AD，根据SAS证明△ABE≌△FDA，得出对应边相等即可.

（2）由全等三角形的性质得出∠AEB= ∠FAD，求出∠AEB+∠BAE=60°，得出∠FAD+∠BAE=60°，即可得出∠EAF的度数.

【规范解答】（1）证明：∵四边形ABCD是平行四边形，

∴∠BAD=∠BCD=120°，∠ABC=∠ADC，AB=CD，BC=AD.

∵△BCE和△CDF都是正三角形，

∴BE=BC，DF=CD，∠EBC=∠CDF=60°.

∴∠ABE=∠FDA，AB=DF，BE=AD.

在△ABE和△FDA中，

∴△ABE≌△FDA（SAS），

∴AE=AF.

（2）∵△ABE≌△FDA，

∴∠AEB=∠FAD.

∵∠ABE=60°+60°=120°，

∴∠AEB+∠BAE=60°，

∴∠FAD+∠BAE=60°，

∴∠EAF=120°-60°=60°.

【反思回顾】这道几何考题主要考查对平行四边形的边角关系（对边相等、对角相等、邻角互补等性质）、作图语句的阅读理解，并在此基础上寻找和证明全等三角形（△ABE≌△FDA）.由于上述考点都是基础题级别，所以解答时不能随意跳步骤，要严谨规范，做到会而不错.

例2（2015·南通）如图2，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD.

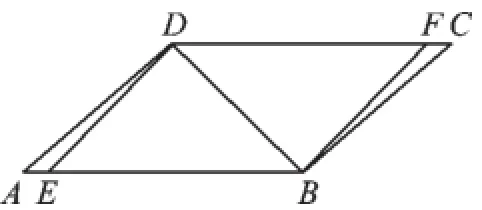
图2

（1）求证：△AED≌△CFB；

（2）若∠A=30°，∠DEB=45°，求证：DA= DF.

【思路讲解】

（1）由四边形ABCD为平行四边形，利用平行四边形的性质得到对边平行且相等，对角相等，再由垂直的定义得到直角相等，利用等式的性质得到角相等，利用ASA即可得证.

（2）由特殊角45°的启发，添加辅助线“如图3，过点D作DH⊥AB，垂足为H”，一方面，在Rt△ADH中，利用30度所对的直角边等于斜边的一半得到AD=2DH，在Rt△DEB中，利用等腰直角三角形的性质得到EB= 2DH，从而得到DA=EB.另一方面，由△AED≌△CFB得到AE=CF，由四边形ABCD是平行四边形得到AB=DC，从而证得EB=DF，再等量代换可证.

【规范解答】

证明：（1）∵四边形ABCD是平行四边形，

∴AD=CB，∠A=∠C，AD∥CB，

∴∠ADB=∠CBD.

∵ED⊥DB，FB⊥BD，

∴∠EDB=∠FBD=90°，

∴∠ADE=∠CBF.

∴△AED≌△CFB（ASA）.

（2）如图3，过点D作DH⊥AB，垂足为H，在Rt△ADH中，∠A=30°，∴DA=2DH.

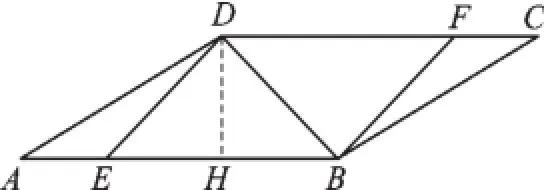
图3

在Rt△DEB中，∠DEB=45°，

∴EB=2DH.∴DA=EB.

∵△AED≌△CFB，∴AE=CF.

∵AB=DC，∴EB=DF.

∴DA=DF.

【反思回顾】一般以平行四边形为载体的证明问题是解答题中的必考题型，由于中考题追求一定的综合性，所以往往这类证明题都会有2～3个小问，而除了第1小问是单一知识点的证明外，第2或3问都会出新的“强化条件”（如例题的第（2）问增加了特殊锐角30°、45°），这时受到这些特殊角度的启发添加辅助线构造特殊直角三角形成为破题的关键.如上面的证明步骤中，强调“在Rt△ADH中”是重要的，是一种聚焦图形的语句，起着引导阅卷老师关注的作用，值得同学们重视.

（作者单位：江苏省海安县城南实验中学）