幂的运算在生活中的应用

刘兴龙



幂的运算在生活中的应用

刘兴龙

幂的运算性质既是进行整式乘除法的基础，同时运用这些知识又可以解决生活中的一些实际问题.本文就建立幂的运算模型，解决实际问题举几个例子与同学们共享.

例1果农王大爷的一块梨园呈梯形，贝贝帮王大爷测得梯形的两条底边的长分别是3（x+y）5和5（x+y）5，其高为（x+y）3，你能根据这个测量结果算出王大爷的这块梨园的面积是多少吗？

【解析】要求这块梨园的面积，由已知的量，可直接利用梯形的面积公式，结合幂的运算法则求解.

解：根据题意，得：

例2已知1平方千米的土地上，一年内从太阳得到的能量相当于燃烧1.3×108千克煤所产生的能量，那么我国9.6×106平方千米的土地上，一年内从太阳得到的能量相当于燃烧煤多少千克？

【解析】9.6×106平方千米的土地就相当于9.6×106个1平方千米的土地，由题意即可获解.

解：根据题意，得9.6×106×1.3×108=1.2× 1015（千克），所以一年内从太阳得到的能量相当于燃烧1.2×1015千克的煤.

例3某市环保局欲将一个长为2×103分米，宽为4×102分米，高为8×10分米的长方体废水池中的满池废水注入正方体贮水池净化.那么请你考虑一下能否有一个正方体贮水池将这些废水正好装满？若有，求出该正方体贮水池的棱长，若没有，请说明理由.

【解析】由于正方体贮水池的体积正好等于长方体废水池的体积，而正方体的体积等于棱长的立方，逆用积的乘方法则可得棱长.

解：假设恰好有一个正方体贮水池将这些废水正好装满，则

这些废水的体积=长方体的体积

又因为棱长的立方等于体积，所以有一个正方体贮水池将这些废水正好装满，这个正方体的棱长是4×102分米.

例4明明家有一块长方形的菜地，其长为（x-2b）4（a-2b≠0），宽为（x-2b）3，芳芳只知道自己家的菜地是一个边长为（x-2b）5的正方形，那么你能求出以明明家的菜地面积值为边长的正方形的面积是芳芳家的菜地面积的多少倍吗？

【解析】考虑本题中的代数式均含（x-2b），所以将其看成一个整体，利用面积公式和幂的运算法则求解.

解：根据题意，得

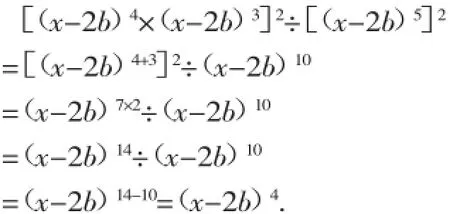
所以以明明家的菜地面积值为边长的正方形的面积是芳芳家的菜地面积的（x-2b）4倍.

例5东风机械厂生产的两种零件都呈三角形形状，已知大三角形的零件的一边等于a6，其边上的高等于a5，小三角形零件的一边等于a4，若大三角形零件的面积等于小三角形零件的面积的a2倍，你能帮助东风机械厂求出小三角形零件的已知边上的高吗？若加工每个小三角形零件需要资金a元，则加工a3个这样的小三角形零件需要多少资金？

【解析】根据大小三角形零件的面积关系，利用面积公式即可求得小三角形零件的已知边上的高，进而进一步求解.

因为加工一个这样的小三角形零件需要资金a元，则加工a3个这样的小三角形零件需要资金为a×a3=a4（元）.

（作者单位：江苏省泰州中学附属初级中学）