基于个体关系属性的加权网络社群结构探测模型

张锴琦，杜海峰

（西安交通大学a.管理学院；b.公共管理与复杂性科学研究中心；c.公共政策与管理学院，西安 710049）

社会人际互动关系中，由相同或相似属性个体所结成的小团体，具有小团体内部个体间关系稠密，小团体之间个体关系稀疏的特征，复杂网络将这种现象称为社群结构特征［1］。由于社群结构能够有效地揭示网络中具有共性节点的结构及特征，因而其研究与应用受到了物理学、管理学、社会学等学科的重视［1-4］。在社会网络研究中，社群结构特征除了表现为个体属性的相似外，还表现为个体关系的亲疏。个体间关系的强弱会影响社群结构特征的分布。因而，对应到网络模型中，这种受到个体关系强弱影响的社群结构称为加权网络社群结构［5］。同时，受到关系强弱的影响，位于社群边缘的个体可能会隶属于多个社群，在结构上表现为社群结构的重叠，使得社群结构特征更为复杂。因而，加权网络的社群结构特征研究在实际社会网络中具有重要的研究意义。

社群结构探测是社群结构特征研究的基础，目前较为通用的社群结构探测方法多通过优化Newman［2］设计的模块性指标，实现对社群结构的探测，如Newman［7］提出的快速探测算法（简称N算法）、Du等［8］提出的基于节点先验知识的探测算法（简称PKM 算法）、Aaron等［9］提出的社群结构探测算法（简称A 算法）、Blondel等［10］提出的社群压缩算法（简称B 算法）等。但是由于经典模块性指标是针对0-1网络提出的，因而上述算法不能有效地实现加权网络的社群结构探测。由于加权网络的社群结构探测需要将权值纳入社群结构的评价体系中，故相比于0-1网络而言，加权网络社群结构概念中的定义元素更加多样，而其探测问题也变得更为复杂［5-6，11］。

Girvan等［12］针对加权网络社群结构提出了一种基于GN（Girvan-Newman）算法的社群结构探测算 法 （Weighted Girvan-Newman Algorithm，WGN）［13］，并同时给出了模块性指标在加权网络中的改进思路。Duch 等［14］将提出的极值优化算法（External Optimization Algorithm，EO）用于改进后的模块性指标Qw，以实现加权网络的社群结构探测。Jin等［15］在WGN 算法的基础上，通过发现社群中心节点，调整非中心节点的方法改进并提出了相应的算法，使得该算法针对大型加权网络具有良好的探测效果。Lu等［16］进一步基于计算群内中心度和群间中心度的方法，提出了相应的加权网络社群结构探测算法。除了上述基于WGN 算法及改进指标优化的探测算法外，一些研究从其他角度重新定义了加权网络社群结构并提出了相应的算法。Farkas等［17］在派系过滤方法的基础上提出了加权派系过滤算法（Clique Percolation Method with Weights，CPMw），用于加权网络社群结构的探测；而Reichardt等［18］提出的Potts模型则是从模糊社群的概念出发，对加权网络社群结构进行探测。然而，上述方法大多只是将权值理解为节点间的多重边，而不是节点间关系亲疏的强度；同时，上述方法鲜有考虑可能存在的社群重叠现象。因而，对于加权网络社群结构探测而言，上述方法存在改进的空间。Ahn等［19］提出了连边社群的概念用于探测具有重叠特征的社群结构，其核心思想认为，尽管一个节点可能属于多个社群，但每一条边的社群含义是相对明确的。因而将对于节点的社群结构探测转向对边的社群结构探测。在连边社群概念基础上，Brian等［20］提出了一种基于概率模型的重叠社群结构探测方法（Principled Statistical Approach for Overlapping Communities，PSOC），其通过构建网络还原模型，并对该模型进行优化来实现社群结构的探测。

受连边社群概念与PSOC 算法设计的启发，本文认为加权网络社群结构的探测应以边为探测的主体，并将边的权值纳入社群结构的探测中，通过计算边与社群的隶属关系来探测网络的社群结构。相比于已有的加权网络社群结构探测算法而言，本文通过将权值转化为距离，用于表示节点间关系的亲疏，并重新定义社群结构概念，使得加权网络中社群内的节点间具有较短的连边距离，社群间的节点间具有较长连边距离；同时，本文采用PSOC算法的概率模型作为基础模型，针对加权网络结构特征改进原有模型，提出相应的探测算法。

1 基于节点关系属性的加权网络社群结构

社群结构特征所表现出的社群内部关系稠密可以解释为社群内的节点总是通过较少的连接边进行联系，节点间关系亲密程度较高。社会网络观点认为节点间距离是节点关系亲疏程度的体现［21］。因而从节点间距离的定义出发，社群结构特征可以描述为社群内节点的平均路径长度较短，而社群间节点的平均路径长度较长。在0-1网络下，节点间的距离表示连接两点最短路径上的边的数量。在加权网络中，由于权值本身就暗含节点间关系强弱的意义，而边的赋权使得节点间的关系可以量化表示，故可以通过节点间的距离来描述加权网络社群结构。如图1所示，图1（a）、（b）分别是2个具有相同网络结构的0-1网络和加权网络；在0-1网络结构下，节点C、A的距离d C-A=2，而节点C、B的距离d C-B=1，从距离上看，节点C、B更应属于同一个社群；而在加权网络结构中，虽然网络结构未发生改变，但由于权值的存在，使得d C-A=0.5+0.5=d C-B=1；相比0-1网络，节点C的社群隶属关系将有更多的可能性。同时，受到引入权值的影响，图1中出现了重叠的社群结构特征。

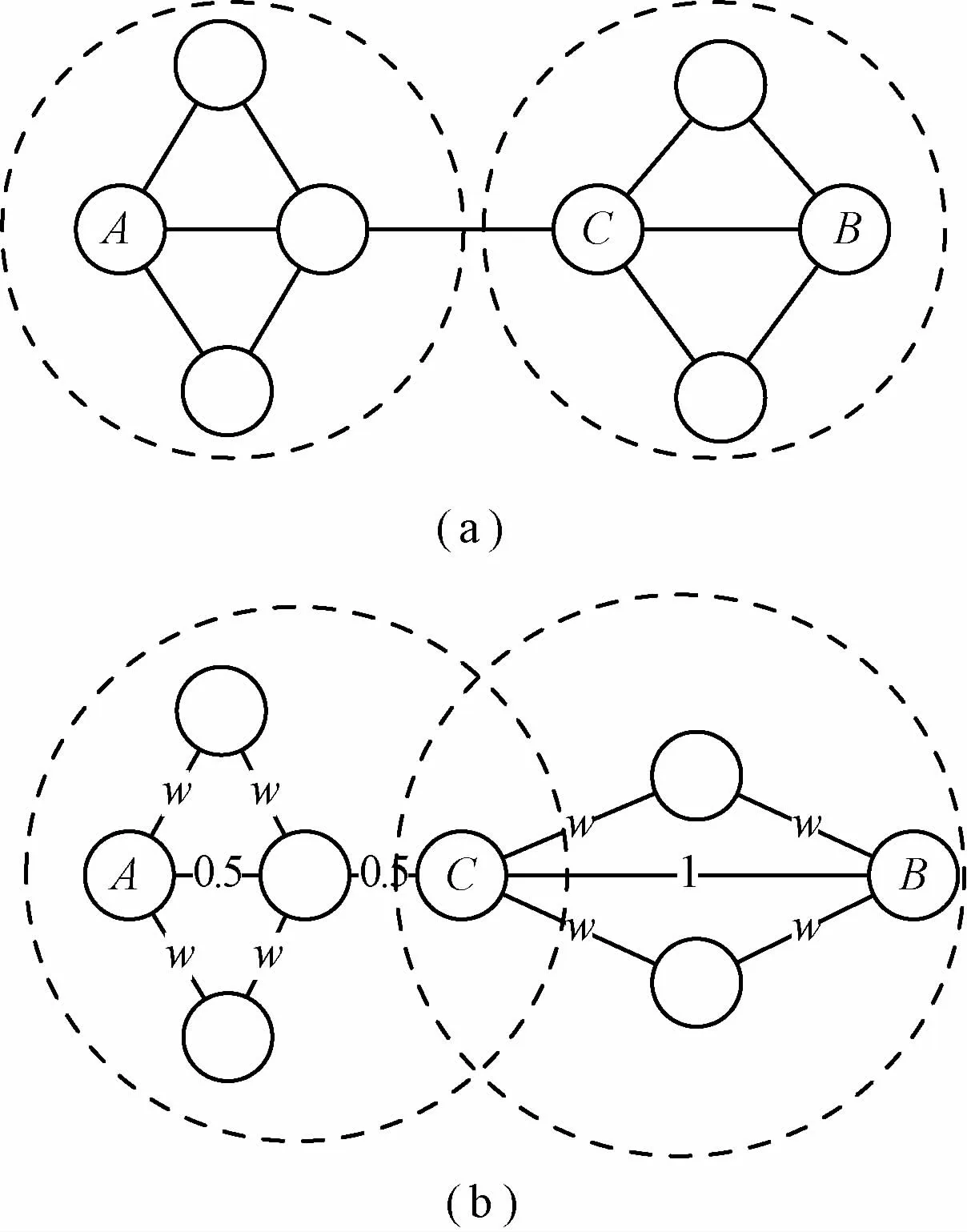
图1 相同结构下0-1网络与加权网络节点距离比较

但是，上述通过权值反映距离，进而描述社群结构的方法并不完全符合Newman等［1］对加权网络社群结构的定义。Newman［13］认为，不是所有的权值都应该纳入社群结构的探测过程中，加权网络社群结构中边的权值是节点间的多重边表示。在对应的WGN 算法中，网络边的居中中心性每次迭代都需要被重新计算，通过删除居中中心性最高的边，以实现社群结构的探测。而权值在该算法中的作用是控制边被删除的次数，即权值为w的某边至多被删除w次。图2所示为WGN 算法对加权网络的社群结构探测结果节点i、j之间边的居中中心性是该网络中最高的，因此，WGN 算法会删除节点i、j之间的边，将节点i、j分置于2个社群。上述结果表明，由于权值只是被视为维系节点间关系有无的条件，故WGN 算法并不能完全反映节点间边的权值对社群结构探测结果的影响。导致上述问题的原因有两方面：①WGN 算法机理强调整体结构，而在一定程度上忽视了边的权值；②WGN 算法及其改进算法的探测结果均强调网络节点在相应社群的单一归属，即节点i一旦被划分到某一个社群，就不会再隶属于其他社群。但对于加权网络的社群结构划分，处于社群边缘的节点，如图2中的节点i、j，由于两者之间的权值较大，使得节点i、j被严格分割在2个社群中并不十分合理，而更合理的探测结果是节点i、j同时隶属于2 个社群，只是隶属程度各有差异。因此，由于节点i、j及其特殊关系的存在，导致了社群的“重叠”。

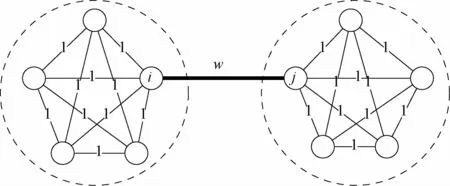
图2 WGN 算法加权网络社群结构探测结果

所谓重叠社群结构是指一个节点可能分属于多个社群的社群结构特征［5］。Ahn等［19］提出连边社群的概念认为虽然节点可能属于多个社群，但一条边属于多个社群的情况并不多见。Brian等［20］基于连边社群的概念提出了PSOC 算法，用于重叠社群结构探测。其算法核心思想是根据边两端节点度值的分布计算边与社群的隶属程度。具体地，PSOC算法认为，边对社群Cz的隶属度q ij（z）取决于边两端节点i、j属于社群C z的期望θiz与θjz，而该期望又受到节点度值的影响。其假设θ·z总体符合泊松分布，因而如果θ·z能够使得生成网络G对原网络的还原概率P获得最大，则生成网络能够在还原网络的同时，通过θ·z反映节点、边和社群的隶属关系，揭示网络中存在的重叠社群结构。PSOC算法采用最大期望估计算法（Expectation-Maximization Algorithm，EM）实现对θ·z的估计，而通过爬山算法实现对估计结果的优化。

虽然PSOC算法是针对0～1网络重叠社群结构探测问题而设计的，但本文认为其计算边的隶属度的过程即是在对边进行重新赋权的过程，而最终结果是通过概率模型使每条边对所有社群的期望加和为1。因而从设计机理而言，该算法可以应用到加权网络之中；其次，PSOC算法通过节点的期望作为计算边隶属度的估计标准，而该期望正是节点通过节点间关系属性分配度值的结果，因而该方法的计算过程符合本文所描述的基于关系属性的加权网络社群结构特征；此外，由于权值的存在，网络可能出现重叠社群结构特征，故其本身符合PSOC 算法的探测对象。基于以上分析，本文以加权网络社群结构探测为研究对象，对于PSOC 算法进行了重新设定及优化方法上的改进，使其能够更加符合加权网络社群结构探测的需要。

2 基于概率模型的加权网络社群结构探测方法

根据以上对于加权网络社群结构概念的讨论以及对PSOC 算法［18］应用于加权网络的机理分析，本文针对加权网络社群结构构建了相应的概率模型和探测方法（Principled Statistical Approach for Communities in Weighted Network，PSCw）。具体地，设网络G=（V，E）包含个节点和条边；节点可被分为K个社群，设Cz表示第z个社群；用对称邻接矩阵A ij表示网络节点i、j之间关系的有无，用wij表示网络中节点i、j连边e（i，j）的权值。设节点i属于社群Cz的期望为θiz，表示以节点i的端点的连边中属于社群Cz的数量；因而对于边e（i，j）而言，其属于社群Cz的期望λij（z）=θizθjz。设权值w ij均匀分布于K个社群中，因而加权后最终边e（i，j）的权值属于社群Cz的期望为

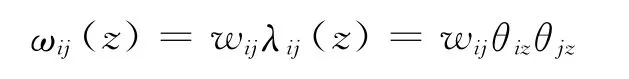
也可解释为边e（i，j）中的权值对社群Cz的隶属度。基于以上对于节点、边与社群概率估计的构建，根据PSOC算法中的概率模型，对于网络G的还原概率为

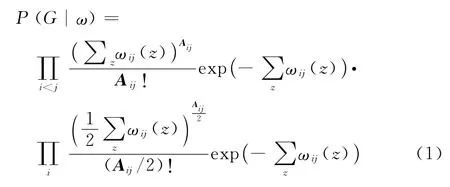
式中，∑zωij（z）为边e（i，j）属于所有社群的期望，即边e（i，j）的权值。理论上，式（1）获得越大，其获得的网络结构与原网络越相似。在采用詹森不等式［20］进行化简后，式（1）可简化为

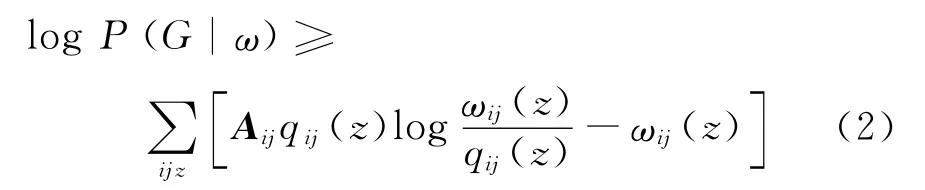
式中：qij（z）为边e（i，j）属于社群Cz的概率，其满足∑z q ij（z）=1，即

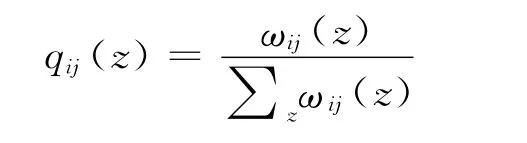
事实上，式（2）中的ωij（z）和qij（z）的物理含义是同质的，其都反映了边与社群的情况。为了进一步获取节点与社群的隶属关系，采用θiz代替ωij（z），即式（2）可表示为

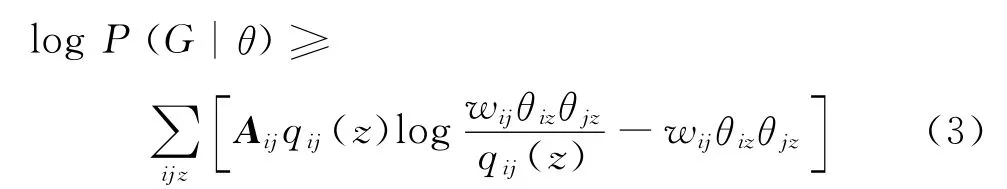
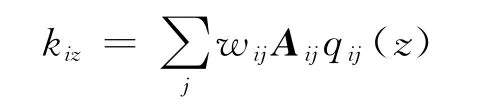
表示以节点i为端点的若干连接边中在社群C z中实际分布的权值；设κz=∑ik iz表示社群Cz中实际拥有的权值；则，且有

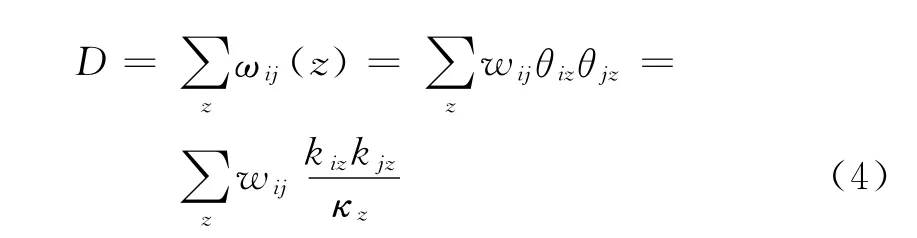
而qij（z）则可表示为

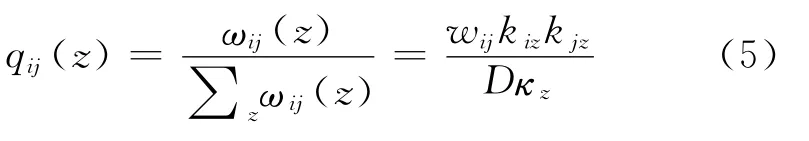
对式（4）中D值求解获得最大，便是在获得式（1）期望最大，即获得网络的最大复原。PSOC 算法中采用EM 算法的步骤来获得期望的最大估计，具体的算法分为计算步骤和剪枝步骤，通过参数反复对期望进行估计求取最大，并不断修正参数，实现结果的收敛；其中计算步骤通过初始的节点特征kiz计算边属于社群的概率qij（z），并同时计算修正后的节点特征；在剪枝步骤中，通过比较和初始容忍度之间差异判断算法是否收敛。算法收敛后计算所得D值为最终优化解，其获得的节点和社群的隶属关系为最终所求社群划分结果。但文献［22］中分析发现，PSOC 算法中的爬山算法很容易使得算法陷入局部最优解中，并且原算法存在隐含并行性和算法多参数影响等问题。因而借鉴文献［22］中算法，本文采用进化算法对上式模型进行优化，以实现加权网络的社群结构探测。

具体地，用矩阵M表示节点与社群关系θiz，并初始建立g个种群

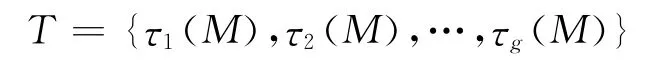
对每个种群τi（M）个体进行最大期望估计求解；以每次期望估计所得的D值作为种群进化的适应度函数；每次迭代选取D值最优的种群进入下一次迭代估计，并同时更新种群τi（M）中的θiz。延用文献［22］中的算法，本文算法中分别引入克隆操作、交叉操作和变异操作等以保持种群的多样性和种群之间的交互，从而更富效率地获得社群结构的划分结果。PSCw 算法基础框架如表1所示。

算法中对于矩阵M的期望估计操作（18～22行）与PSOC算法中计算步骤单次迭代过程一致；克隆步骤（6～9行）、交叉操作（11～14行）、变异操作（15～17 行）与文献［20］中的操作一致；选择操作（25～28行）根据适应度函数D分别计算克隆种群中不同种群的适应度，将D值最优的种群进行保留进入下一次迭代过程。本文优化算法采用迭代次数作为算法的中止条件。算法最终以求得的Dmax所对应的社群划分结果作为算法的最终社群结构探测结果。算法的单次时间复杂度为O（gme K），g为设定种群数量，m为克隆种群数量，e为网络中存在的边的数量，K为初始社群数量。该算法时间复杂度仅与网络规模有关系，而并不受到网络权值的影响，且复杂度在合理范围内。因而该算法可以运用于规模较大且权值复杂的加权网络之中。算法的收敛性证明与基础进化算法类似，此处便不再赘述。

表1 PSCw算法基础框架

3 实验与讨论

对于本文所提PSCw算法的实验包括两部分：①对计算机生成加权网络的社群结构探测；②对实际加权网络的社群结构探测。测试实验均在Intel（R）Core（TM）2 quad CPU q8400 @2.66GHzPC 机 的Matlab7.0平台下完成。算法参数如表2所示。

表2 PSCw算法参数设置

3.1 计算机生成加权网络

计算机生成加权网络选取基准加权网络［13］为实验测试网络。基准加权网络中存在n个节点和k个社群，每个社群内含有k/n个节点；每个节点平均度值为d，其中与社群内的节点连接边数为kin，与社群外的节点连接边数为kout；社群内连接边的权值为win，社群间的连接权值为wout，且一般有win＞wout。在基准加权网络基础上，本文对计算生成加权网络的测试包括两部分：①限定社群内权值win的情况下，不同连接边数kout所构成的网络结构；②限定kout条件下，不同社群内权值win所构成的网络结构。用于测试的网络含有128个节点，分为4个社群，每个社群含有32个节点，除全连接网络外每个节点平均度值为16。实验采用NMI指标［23］作为社群结构探测效果的评价指标，其计算式为

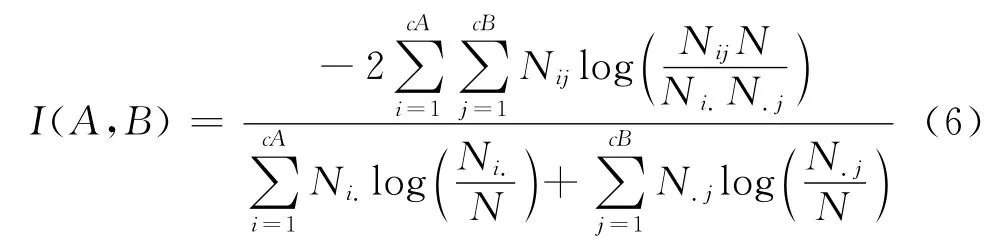
NMI指数越接近1，探测社群结构与实际社群结构越相似，反之差异越大。

对于第1 类网络结构，在限定社群内权值win的情况下，kout的改变意味着网络拓扑结构的改变。对于这类网络的实验旨在算法在加权网络情况下，针对不同网络结构其对于社群结构的探测效果。图3为win的均值等于5，wout的均值等于3的情况下，PSCw 算法对于不同kout的网络结构的探测效果。为了消除网络结构的随机性，对于每个kout分别生成10个独立网络，对每个独立网络进行10次独立运算，以下测试方法与之相同。

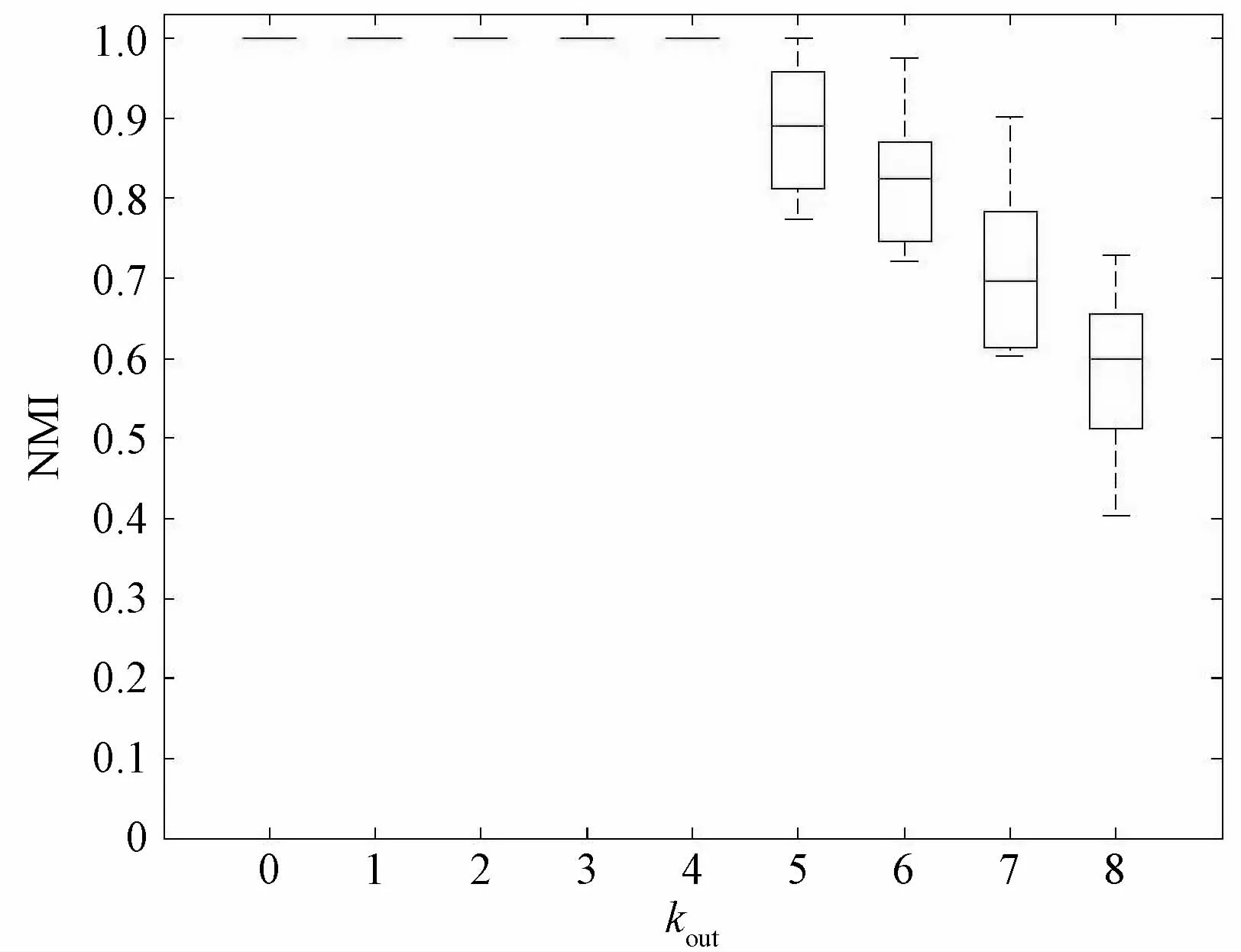
图3 win均值为5时，不同kout网络探测NMI结果

从社群结构探测结果来看，当kout＜5时，网络的社群结构相对较为清晰；此时NMI值始终等于1，说明算法的社群探测结果与原网络划分的社群结构一致。随着kout值的不断变大，节点与社群内外的连接边逐渐一致，在这种情况下，拓扑结构上社群结构已经逐渐模糊，网络权值则成为判断社群结构的主要标准。从结果来看，当kout≥5时，PSCw 也能获得较为满意的结果。但由于权值win与wout的差异并不明显，从权值上一些边也很难区分其社群归属，因而PSCw 算法的探测结果存在一定误差。图4为win的均值等于10，wout的均值等于5的情况下，PSCw 算法对于不同kout的网络结构的探测效果。从结果来看，由于权值的差异加大，社群结构的探测效果要优于图3中的结果。

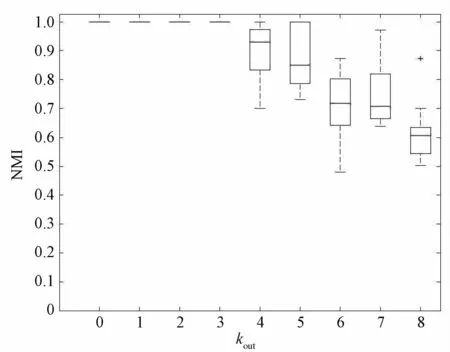
图4 win均值为10时，不同kout网络探测NMI结果

对于第2类网络结构，在限定kout的情况下，不同的权值win所对应的社群结构特征也不相同。当win=wout=1 时，网络等同于0-1 网络结构；而win＞wout时，网络中的社群结构便会受到权值的影响而不同，尤其是在kout≥kin时，拓扑结构上的社群结构特征变得逐渐模糊，权值对于社群结构的影响便尤为重要。图5是限定kout=8的条件下，wout均值等于2，win均值由2～10时，PSCw 算法所得的社群结构探测效果。

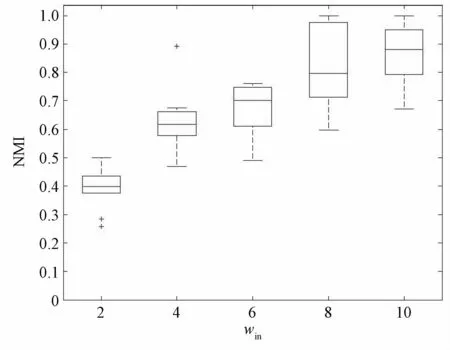
图5 kout=8时，不同win网络探测NMI结果

从结果来看，在win均值等于2时，社群内外的权值基本保持一致，无论从拓扑结构上还是从网络权值上，网络社群结构特征均不明显，因而，此时PSCw 算法的探测结果也相对较差。而随着win均值的不断增大，即使网络拓扑结构上的社群结构特征不明显，但从权值上也能逐渐地区分出社群结构，因而PSCw 算法的探测效果不断提高。当win均值等于10时，通过网络权值已经能够较好地区分出社群内和社群外的连接边，因而PSCw 算法也获得了较好的结果。从实验结果来看，PSCw 算法能够在社群内外权值区分较明显，而拓扑结构不明显的情况下，探测出加权网络的社群结构特征。

综合以上两种生成网络的实验结果而言，PSCw 算法既能够在拓扑结构固定的情况下，较好地探测出不同权值的网络社群结构，也能在权值固定的情况下，较好地探测出不同拓扑结构的网络社群结构。因而从计算机生成网络的结果来看，PSCw 可以适用于加权网络的社群结构探测。

3.2 实际加权网络

为了进一步验证PSCw 算法的探测效果，本文对PSCw 算法在实际加权网络的社群结构探测进行了实验。实验基于西安交通大学人口与发展研究所于2005年深圳市农村流动人口调查的整体网络数据进行。本文选取了调查数据中CZ公司的整体网络作为实验数据。其包含了该公司农民工流动人口实际支持、情感支持和社会交往支持等3个社会支持网络，以及婚姻讨论、生育及子女教育讨论、避孕讨论和养老讨论等4个社会讨论网络。但是由于此次调查仅针对支持或讨论关系的有无，因而每个网络都是一个0-1网络，因此，本文在实验过程中对这些网络进行了叠加处理。这种处理除了使测试网络成为加权网络外，还具有一定的社会学意义，其表示了一种复合性的社会支持网络或社会讨论网络，这种由多个网络构成的网络结构能够更全面地反映被调查者的支持或讨论关系，因而其社群结构也能够更真实地揭示被调查者的实际社群关系。因此，本文测试的数据包含三部分，其分别为叠加社会支持网络、叠加社会讨论网络以及将社会支持和社会讨论相叠加的社会网络（简称复合社会网络），相应的网络属性如表3所示。

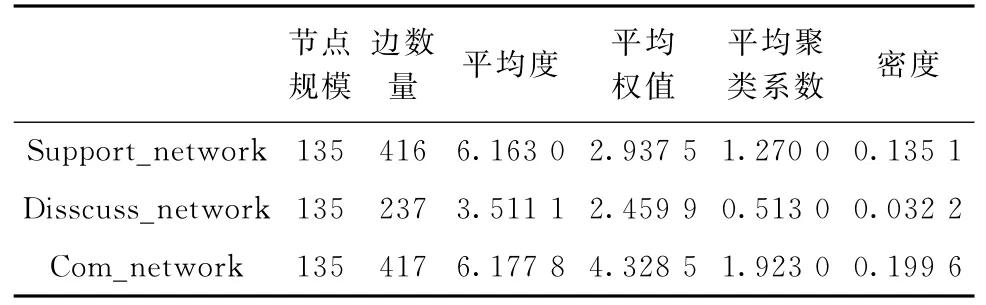
表3 测试实际网络属性

由于PSCw 算法需要预先设定网络中的社群数量，故本文采用N 算法［5］对其进行预探测获得社群数量。结果表明，该公司的7个网络中平均包含5.8个社群，其中，社会支持网络平均包含5.3个社群，社会讨论网络平均包含6.2个社群。因而在采用PSCw 算法进行探测时，依照向下取整的原则分别设定社会支持网络K=5，社会讨论网络K=6，复合社会网络K=5。图6（a）～（c）分别表示叠加社会支持网络、叠加社会讨论网络以及复合社会网络的探测结果。

从结果来看，PSCw 算法能够较好地区分网络中存在的社群结构，并且该划分也较好地体现了网络中的权值对于社群结构的影响。如图6（b）中，节点64、110由于权值的影响，其虽然在结构上应附属于另一个节点90所在社群，但PSCw 算法仍将其判断为一个独立的社群。同时，PSCw 算法可以识别网络中位于社群重叠部分的节点。图7表示3组测试网络中位于社群重叠部分的部分节点与社群的隶属程度。

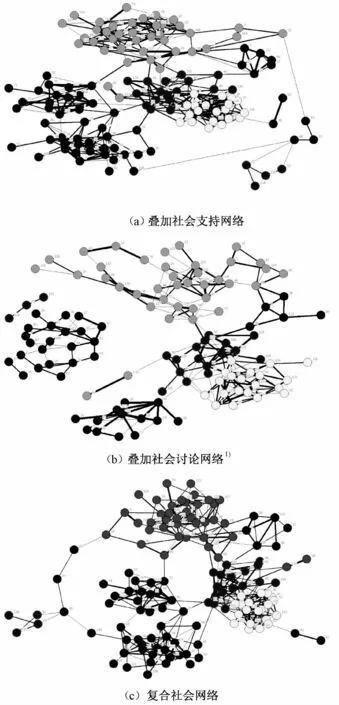
图6 PSCw 算法对实际网络探测结果

图7中节点至少与2个社群拥有较高的隶属度关系，因而这些节点位于社群结构的重叠部分。在社会网络分析过程中，这类节点大多位于社群的边缘结构或结构洞位置，能够有效控制网络资源，具有一定的社会学意义。而准确的隶属度值则能够在一定程度上解释这种结构形成的原因，进而可以对网络进行更深层次的分析。

总体而言，PSCw 算法能够较好地应用于实际网络的社群结构探测，同时，由于PSCw 算法能够准确地计算网络中节点对社群的隶属度，也为社群结构特征在实际研究中的应用拓宽了领域。但需要说明的是，由于PSCw 算法在探测过程中无法对算法的社群数量进行有效收敛，故图6（a）、（c）中节 点52、72、118、135 形 成 社 群 与 节 点120被划归为一个社群，这可能在一定程度上影响了社群结构探测效果，因而需要在进一步的研究工作中予以克服。

图7 3组测试网络部分节点与社群隶属关系

4 结语

本文基于节点间关系的亲疏对加权网络社群结构进行了重新定义，加权网络的社群结构不仅表现为节点连接边的稠密，而且应表现为节点关系的紧密，同时，权值会使得社群结构出现重叠的特征。受到连边社群概念的启发，本文在PSOC 算法基础上改进并提出了针对加权网络社群结构的探测模型及优化算法——PSCw 算法，将网络结构与权值纳入到一个统一的模型中进行计算。通过在计算机生成网络的实验发现，PSCw 算法能够在不同网络拓扑结构和不同权值分布的情况下对加权网络中的社群结构进行有效探测；在对实际加权网络的探测过程中，PSCw 算法也能给出符合原网络实际的社群结构划分，并且获得了节点隶属于社群的信息，为相关社会问题的定量化研究提供了方法支持。通过研究发现，在加权网络社群结构探测过程中，节点与社群隶属关系的量化能够更好地反映网络真实情况和深层内涵，尤其是针对具有现实意义的社会网络结构。因此，在进一步的研究中需要探求节点与社群隶属程度的现实社会学意义。然而，受到PSOC 算法概率模型原始假定的限制，PSCw 算法仍然是一种分类算法，在社群结构未知的情况下，该算法不能对社群数量进行较好的收敛。因此，在未来的研究过程中需要进一步完善。