基于引力搜索算法的漏磁缺陷重构*

韩文花，王　建，汪胜兵，吴正阳，王　平

（1.上海电力学院自动化工程学院，上海　200090；2.南京航空航天大学自动化学院，南京210016）

基于引力搜索算法的漏磁缺陷重构*

韩文花1，王建1，汪胜兵1，吴正阳1，王平2

（1.上海电力学院自动化工程学院，上海200090；2.南京航空航天大学自动化学院，南京210016）

缺陷重构，即从漏磁信号反演出铁磁性材料的缺陷轮廓或几何参数，是漏磁无损评估中的一个重要研究方向。针对缺陷漏磁信号特征及缺陷轮廓特征的复杂性，提出基于引力搜索算法的漏磁缺陷重构方法。依据磁偶极子模型理论分析提取实测漏磁信号有效信息段，径向基函数神经网络作为前向模型，引力搜索算法作为迭代算法，利用其在高维解空间中避免陷入局部最优的能力，得到最优缺陷轮廓，实现缺陷重构。仿真和实验结果表明，基于引力搜索算法的缺陷重构方法能提高重构精度和效率，具有较高的实用价值。

铁磁性材料，漏磁检测，缺陷重构，磁偶极子模型，引力搜索算法

0　引言

漏磁检测，作为无损检测中常用的一种检测方法，检测对象为铁磁性材料，该方法对材料表面状态要求不高，检出深度也较大，易于实现自动化检测，使得漏磁检测目前广泛应用于由铁磁性材料制成的军用装备、风电场设备、石油、天然气输送管道和储油罐等的缺陷检测［1-3］。在漏磁检测中，使用永久磁铁或电流磁化检测样本，并用霍尔传感器采集漏磁信号，再进行数据分析。求解反演问题上，即通过漏磁信号得到相应的缺陷轮廓，普遍采用的有基于智能算法的迭代方法［1］、神经网络反演法［2］、改进优化算法结合神经网络法［4］、贝叶斯估计法［5］等重构缺陷轮廓。由于群智能优化算法简单、参数少、易实现等优点，在无损检测领域已广泛应用［6-7］。

本文将提出一种新的缺陷重构方法，依据磁偶极子模型理论［8-9］，分析提取有效漏磁信息段用来进行缺陷重构，从而降低计算量，提高缺陷重构的效率；采用引力搜索算法（Gravitational Search Algorithm，GSA）［10］作为重构过程的迭代算法，由于GSA算法能有效避免缺陷重构过程中陷入局部极值，从而可提高缺陷重构的精度。

1　理论分析

1.1缺陷漏磁场的数学模型——磁偶极子

工件在磁场中饱和磁化时，缺陷周围产生的漏磁场，把缺陷的两个侧面看作两个磁偶极子，用磁偶极子模型［8-9］来模拟缺陷周围的漏磁场。基于磁偶极子模型理论，一个缺陷宽度为2 δ的点孔状、洞状的工件表面裂纹缺陷可由等效点偶极子模型来模拟，如图1所示：

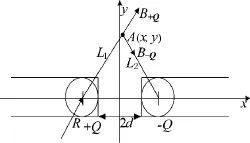
图1　磁偶极子模型示意图

图1中，±Q表示磁偶极子所带的磁荷量，L1、L2表示磁偶极子到检测点A（x，y）的距离，y为提离距离，缺陷宽度为2 δ，磁荷半径为R，计算中不予考虑，则在检测点A（x，y）处产生的磁场，在x，y方向的两个分量为：

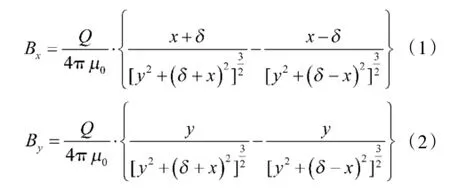
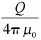
图2　缺陷漏磁场Bx分布形态　图3　缺陷漏磁场By分布形态

图2与图3中，曲线依次分别对应2 δ取值为1 mm、3 mm、5mm、7mm、9mm、14mm。从图中可以看出，缺陷宽度2 δ增大时，Bx、By的幅值和在x方向的跨度均随之增大，而且在x方向的跨度均大于缺陷的宽度（通常为缺陷宽度的2倍～5倍），但当δ取值大于提离距离y（图中2 δ为9 mm）时，出现福斯特理论［11］（将凹槽上方的漏磁场近似为半圆形的磁力线）相似现象，Bx出现双峰，此时磁偶极子模型对漏磁场的模拟效果变差，因此，实际测量漏磁信号时提离距离不能取得过小。而By在缺陷中心两侧各有一个正向、负向峰值，而只有一个位于缺陷中心的正向峰值（提离距离合适时），且Bx在x方向的跨度比By小，与缺陷宽度对应关系更明显。从信号反演的角度来看，采集漏磁信号分量Bx，采用磁偶极子模型理论分析提取有效信息段对缺陷轮廓或几何参数进行反演，以提高反演效果及提高反演效率在理论上是可行的。

1.2引力搜索算法

伊朗的克曼大学教授Esmat Rashedi等人于2009年提出了引力搜索算法［10］，且在求解高维空间优化问题时，其寻优精度和收敛速度都要明显优于粒子群优化算法和遗传算法等优化算法。在GSA算法中，将优化问题的解抽象为粒子，根据粒子的适应度值来间接计算粒子的惯性质量，惯性质量的大小间接反映粒子所在位置的优劣，粒子间通过相互之间的万有引力实现优化信息共享，由于万有引力的作用会使粒子朝着惯性质量最大的粒子移动，而质量最大的粒子占据最优位置，从而求出优化问题的最优解。在该算法中，每个粒子赋予4个特征量：位置、惯性质量、主动引力质量和被动引力质量，物体的位置就是问题的解。在一个D维的搜索空间中，假设有N个粒子，定义第i个粒子的位置为：

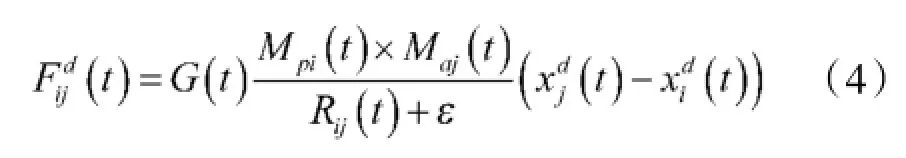
其中Mpi（t），Maj（t）分别为相互作用粒子（被作用粒子i、作用粒子j）的惯性质量，ε为一个很小的常量，G（t）为时刻t的引力常数，Rij（t）为粒子i与粒子j之间的欧氏距离。式（5）中G0等于100，α等于20，T为迭代的总次数。

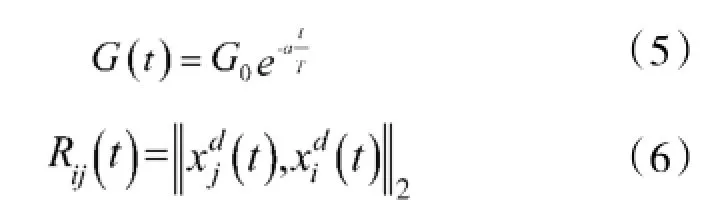
遵循运动学规律，则作用在粒子i上第d维上的总作用力是来自其他所有粒子的引力之和：

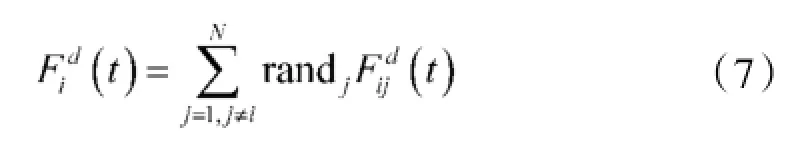
其中，randj是为了给引力搜索算法增加随机特性，是［0，1］之间的一个随机数。根据牛顿第二定律，t时刻粒子i在第d维上的加速度（t）为：

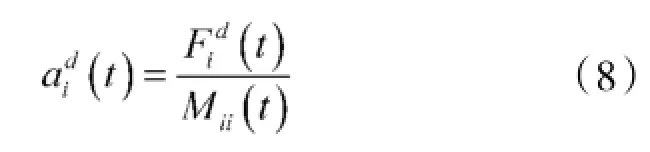
其中，Mii（t）为t时刻粒子i的惯性质量，是依据粒子的适应度值来计算的，粒子的惯性质量越大，表明该粒子越接近最优解，同时意味着它对其他粒子的吸引力越大，但其具有的加速度会变小，移动速度会越慢。在GSA算法中，主动引力质量和被动引力质量均为粒子的惯性质量，通过式（9）～式（11）更新：

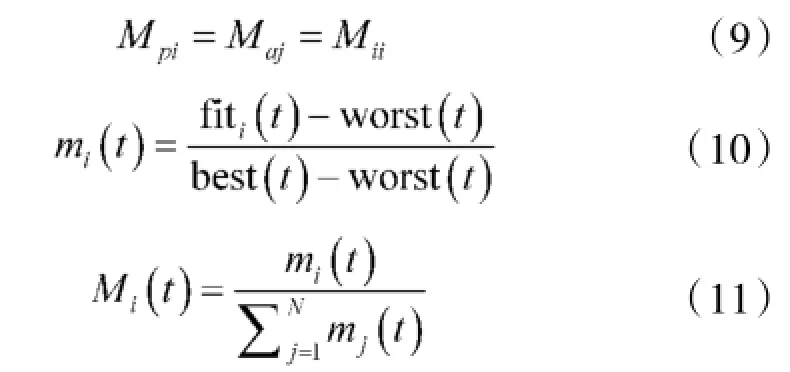
式

（10）中，fit（t）为时刻t时粒子的适应度值。对求解最小值问题，worst（t）和best（t）定义为：

对求解最大值问题，worst（t）和best（t）定义为：

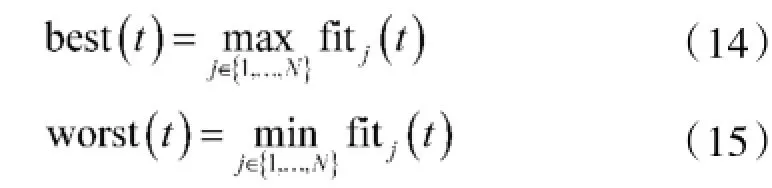
仿照运动学规律，迭代过程中粒子的速度和位置更新，根据式（16）与式（17）进行：

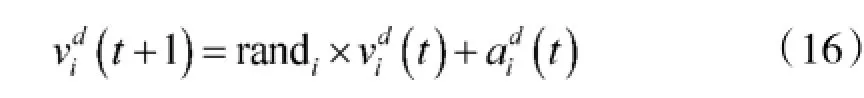
式（16）中的randi与式（7）中的randj均为增加算法的随机特性。

为进一步提高该算法的搜索效果和节省时间成本，可随着迭代的进行逐步减少式（7）中的粒子数量，即随着迭代的进行舍弃惯性质量较小的粒子对其他粒子的作用。用Kbest（t）表示第t次迭代时参与对其他粒子作用的一组惯性质量较大的粒子数量，Kbest（t）假设为一个随迭代次数增加而减小的线性函数。Kbest（t）的初始值为搜索粒子的数量（所有的粒子都作用于其他粒子上），Kbest（t）的最终值为1，即最后只有惯性质量最大的粒子作用于其他粒子，因此，式（7）重新定义为：

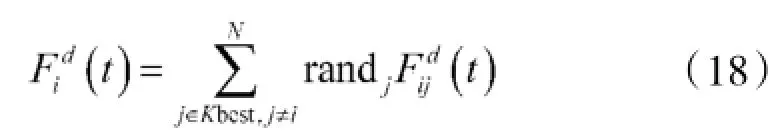
2　基于引力搜索算法的漏磁缺陷重构

本文提出基于引力搜索算法的漏磁缺陷重构方法，主要包括两个部分，使用磁偶极子模型理论分析，提取漏磁信号分量Bx的有效信息段作为缺陷重构信号；迭代寻优过程的实现由GSA算法来实现。径向基函数神经网络作为前向模型［12］，用来从缺陷轮廓X=［x1x2…xN］预测出漏磁信号Y=［y1y2…yN］。该模型由210组缺陷轮廓和对应漏磁信号训练得到。用实测漏磁信号P=［p1p2… pN］与预测漏磁信号Y=［y1y2…yN］之间的误差平方和作为优化问题的适应度函数，其计算公式如下：

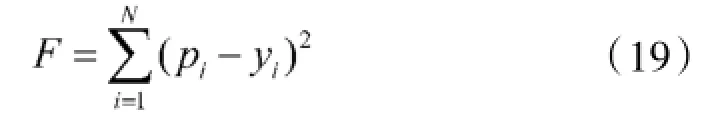
适应度值的大小反映实测信号与预测信号之间的误差大小，从而也间接反映重构的缺陷轮廓与真实轮廓之间误差大小，计算时实际信号长度为有效信息段长度。基于引力搜索算法的缺陷重构方法的实现过程如下页图4所示。

3　仿真与实测实验结果

3.1仿真实验结果

实验中采用密歇根州立大学电子与计算机工程系Udpa教授与Pradeep Ramuhalli博士提供的漏磁信号数据库［2］，该漏磁信号数据库由ANSYS软件仿真了240组不同宽度和深度的（宽度在2.54 cm～17.78 cm之间变化，深度在0.381 cm～2.159 cm之间变化）二维缺陷样本并得到的漏磁信号分量Bx组成。同样，仿真实验中使用210组缺陷-信号样本对训练神经网络前向模型，剩余30组用于仿真实验。由ANSYS软件仿真缺陷样本（宽度为2.54 cm，深度为0.762 cm）得到的漏磁信号分量Bx，依据磁偶极子理论对漏磁场分量Bx的分析，进行缺陷重构时，提取漏磁信号有效信息段（出现峰值的波形段），如图5所示，其中虚线部分为有效信息段。

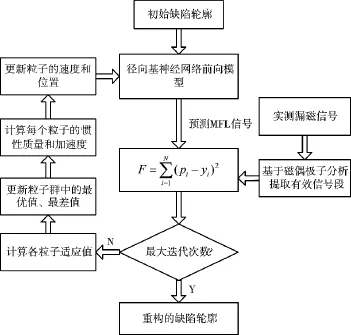
图4　基于引力搜索算法的缺陷重构方法框图

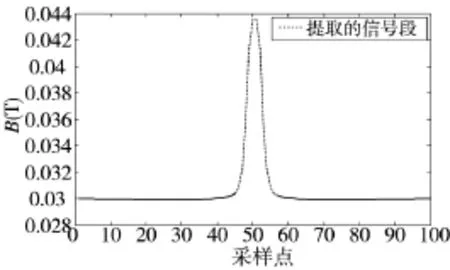
图5　基于磁偶极子模型提取的缺陷有效漏磁信息段

图6　对宽12.7 cm，深度0.635 cm的缺陷重构结果

图7　对宽9.652 cm，深度1.27 cm的缺陷重构结果

图8　对宽2.54 cm，深度1.397 cm的缺陷重构结果

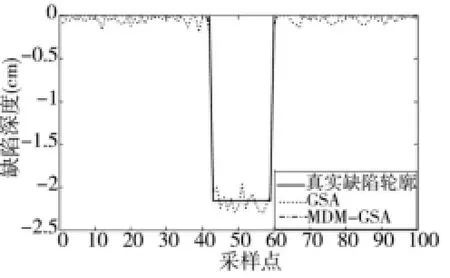
图9　对宽8.636 cm，深度2.159 cm的缺陷重构结果

本文提出的重构方法，与基于遗传算法、改进粒子群算法的缺陷重构方法［13-14］类似，智能优化算法采用全局优化性能好的GSA算法，不同之处在于，在重构时采用漏磁信号长度为有效信息段的长度，由于该方法是根据磁偶极子模型理论分析提取的有效信息段，故称此法为基于MDM-GSA的缺陷重构方法。图6～图9中为采用基于GSA与基于MDM-GSA的缺陷重构方法，对4个不同尺寸的缺陷进行轮廓重构，图中实线为真实的缺陷轮廓，虚线为基于GSA方法的缺陷重构轮廓，点划线为基于MDM-GSA方法的缺陷重构轮廓。从图中可以看出，基于GSA方法的重构缺陷轮廓均出现较大的误差，基于MDM-GSA方法重构的缺陷轮廓更接近真实缺陷轮廓，尤其对深度较大的缺陷其重构结果误差更小，几乎与真实轮廓重合。

此外，引入重构轮廓和真实轮廓之间出现的最大误差值作为精度评价指标，迭代次数及仿真时间作为重构效率评价指标。表1给出了图6～图9中采用基于GSA重构方法与基于MDM-GSA的重构方法得到的重构缺陷结果的最大误差值、迭代次数及仿真时间。

从表1中可以看出，最大误差值明显减小，迭代次数及仿真所用时间也短得多，基于MDM-GSA的重构方法得到的缺陷轮廓更接近真实的缺陷轮廓，而且在重构的效率上也有很大的提高。

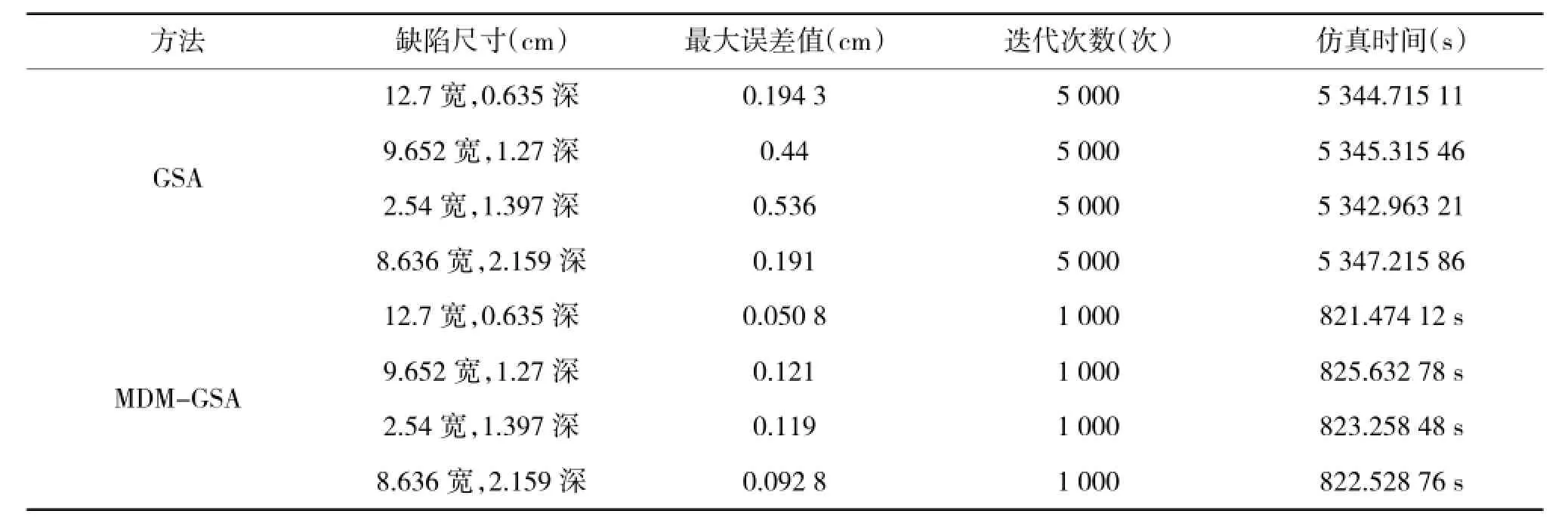
表1　两种方法的误差、迭代次数及仿真时间比较

3.2实测实验结果

为了进一步验证本文所提方法对实测漏磁信号的重构效果及实用价值，采用实测漏磁信号进行缺陷重构。实验装置系统如图10所示，由漏测实验平台和漏磁检测装置两部分组成。为了增加检测过程的延续性，漏磁实验平台设计为转盘式，转盘的材料采用钢轨材料U71Mn，在其表面加工一系列不同尺寸（宽度、深度）的缺陷样本。转盘的线速度范围为2 m/s～50 m/s，由电机控制转速；漏磁检测装置由正、反方向励磁装置（反向励磁装置对钢轨测试样本方向磁化，消除每次对测试样本进行正向磁化时不受上次磁化后的剩磁影响）、霍尔感应器探头、信号调理电路、数据采集卡（采用ADLINKDAQ2204数据采集卡）及PC机构成。

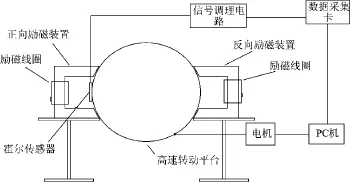
图10　实验装置示意图

实验时设置霍尔传感器与钢轨的提离距离为1 mm，数据采集采样频率为120 KHz，经调理电路霍尔传感器探测到的毫伏级别检测信号放大到±10 V范围内。图11为实验检测到的7个凹槽型缺陷漏磁信号分量Bx。

图11　实测的漏磁信号Bx分量

实测缺陷漏磁信号为霍尔感应器感应磁场得到的电压信号，并在采集过程进行了放大处理100倍的处理。此外整个检测过程在霍尔感应器探头和转盘钢轨存在相对运动的情况下完成，不可避免地得到的漏磁信号含有噪声成分。因此，对实测信号进行缺陷轮廓重构时，首先对实测进行了预处理，预处理过程包括对实测信号进行还原处理（还原为漏磁场的磁场强度值）和重采样处理。

采用仿真实验中训练好的RBFNN作为前向模型，图12、图13为两个实测缺陷样本（样本1宽0.04 cm，深0.6 cm；样本2宽0.04 cm，深0.4 cm）的漏磁信号经预处理后由的轮廓重构结果，图中实线为真实的缺陷轮廓，虚线为基于GSA方法的重构缺陷轮廓，点划线为基于MDM-GSA方法的缺陷重构轮廓。表2给出了对两个缺陷样本进行重构时的最大误差值、所用迭代次数及时间。

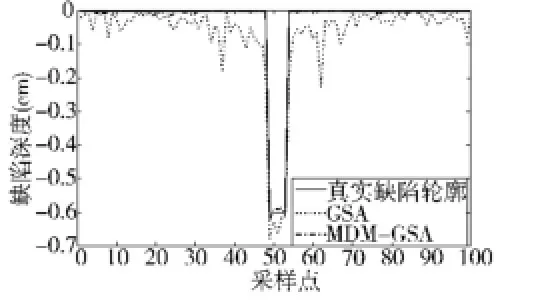
图12　对宽0.04 cm，深度0.6 cm的缺陷重构结果

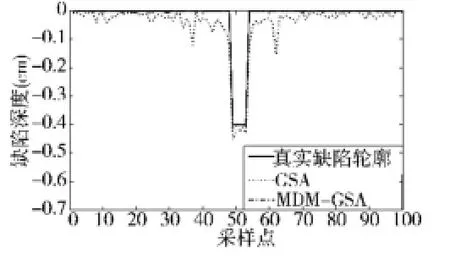
图13　对宽0.04 cm，深度0.4 cm的缺陷重构结果

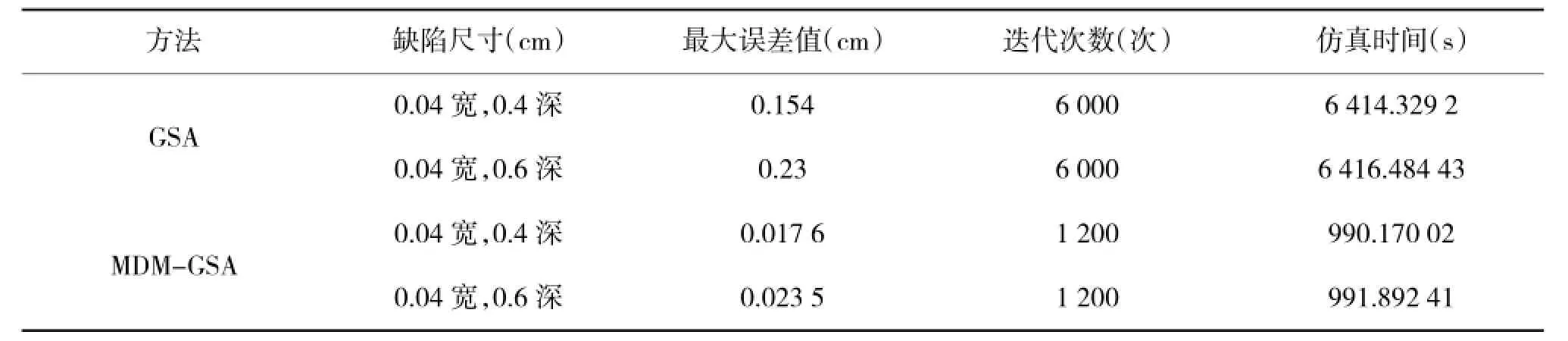
表2　两种方法的误差、迭代次数及仿真时间比较

从图12、图13及表2中可以看出，实验结果取得与仿真结果类似效果。基于MDM-GSA方法的重构轮廓误差小、更接近真实缺陷轮廓，而且仿真时间也要少得多。仿真及实测实验结果均表明，本文提出的缺陷重构方法具有效率、精度高的特点，同时也对实测信号数据中的噪声具有鲁棒性等实用性特点，可以更好地完成缺陷的轮廓重构，是一种有效实用的漏磁反演重构方法。

4　结论

提出了一种基于引力搜索算法的缺陷重构方法，用于由所测漏磁信号重构缺陷轮廓。该方法利用磁偶极子模型理论分析提取漏磁信号的有效信息段，获取最能代表缺陷漏磁场的信号区间，结合启发式优化算法——引力搜索算法在处理高维空间优化问题时具有的高效优化能力，求解逆问题中的全局最优解。从仿真与实测实验结果可以看出，该方法能高效、准确地重构出缺陷轮廓，实用价值高。

［1］PRIEWALD R H，MAGELE C，LEDGER P D，et al.Fast magnetic flux leakage signal inversion for the reconstruction of arbitrary defect profiles in steel using finite elements［J］. IEEE Transactions on Magnetics，2013，49（1）：506-516.

［2］RAMUHALLI P，UDPA L，UDPA S S.Electromagnetic NDE signal inversion by function-approximation neural networks ［J］.IEEE Transactions on Magnetics，2002，38（6）：3633-3642.

［3］雷良金，王长龙，孙世宇，等.基于蚁群算法的径向基网络漏磁信号二维反演［J］.火力与指挥控制，2011，36（3）：163-165.

［4］傅荟璇，刘胜，王宇超.改进粒子群-BP神经网络的二维缺陷重构［C］//Proceedings of the 31st Chinese Control Conference，2012：25-27.

［5］苑希超，王长龙，王建斌.基于贝叶斯估计的漏磁缺陷轮廓重构方法研究［J］.兵工学报，2012，33（1）：116-120.

［6］丁攀，吕福在，项占琴.基于小波包分解和支持向量机的石油套管缺陷智能识别［J］.钢铁研究学报，2012，24（5）：58-62.

［7］韩文花，徐俊，沈晓晖，等.自学习粒子群与梯度下降混杂的漏磁反演方法［J］.火力与指挥控制，2015，40（1）：88-91.

［8］曹印妮.基于漏磁成像原理的钢丝绳局部缺陷定量检测技术研究［D］.哈尔滨：哈尔滨工业大学，2007：22-27.

［9］蒋琦.管道漏磁检测量化技术及其应用研究［D］.天津：天津大学，2002：25-27.

［10］RASHEDI E，NEZAMNADI-POUR H，SARYAZDI S.GSA：Gravitational search algorithm［J］.Information Science，2009，179（13）：2232-2248.

［11］美国无损检测学会.美国无损检测手册：电磁卷［M］.第2 版.《美国无损检测手册》译审委员会译.上海：上海世界图书出版公司，1999：874，943-947.

［12］HAYKIN S.Neural networks：a comprehensive foundation ［M］.New Jersey：Prentice-hall，2001.

［13］韩文花，阙沛文.基于遗传优化算法的二维漏磁缺陷重构［J］.中国石油大学学报（自然科学版），2006，30（1）：138-141.

［14］HAN W H，XU J，YANG P.Defect profile estimation from magnetic flux leakage signal via efficient managing particle swarm optimization［J］.Sensors，2014，14：10361-10360.

Defect Reconstruction from Magnetic Flux Leakage Signals Based on Gravitational Search Algorithm

HAN Wen-hua1，WANG Jian1，WANG Sheng-bing1，WU Zheng-yang1，WANG Ping2
（1.School of Automation Engineering，Shanghai University of Electric Power，Shanghai 200090，China；2.School of Automation，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

Defect reconstruction，which is inversion of the defect profile or geometrical parameters of ferromagnetic material from magnetic flux leakage（MFL）signal，has been one crucial research of MFL nondestructive evaluation.For the complexity to obtain defect geometry feature，a new inversing approach based on gravitational search algorithm （GSA）is proposed.According to magnetic dipole modeling theoretical analysis，the effective information segment from the measured MFL signal，the radial-basis function neural network is utilized as forward model，and GSA is used as iterative algorithm because its avoiding falling into the local optimal solution in high dimensional space.The new approach can obtain the optimal defect profile to achieve defect reconstruction.Both the simulation results and the experiment ones show that the GSA-based defect reconstruction approach can improve the reconstructing accuracy and efficiency and has high practical value.

ferromagnetic material，magnetic flux leakage inspection，defect reconstruction，magnetic dipole model，gravitational search algorithm

TP73

A

1002-0640（2016）07-0097-06

2015-06-12

2015-07-09
*

国家自然科学基金（51107080，61304134）；上海市电站自动化技术重点实验室基金（13DZ2273800）；上海市重点科技攻关计划基金资助项目（14110500700）

韩文花（1976-），女，山东日照人，博士，副教授。研究方向：无损检测、漏磁反演、智能优化算法等。