边坡位移场对弹性模量和泊松比的灵敏度分析

王鹏（重庆交通大学 河海学院，重庆 400074）

边坡位移场对弹性模量和泊松比的灵敏度分析

王鹏
（重庆交通大学 河海学院，重庆 400074）

介绍了ABAQUS总位移法求解设计变量为材料参数的灵敏度分析原理，以摩尔库伦模型作为本构，建立了单级边坡的均质、非均质的模型，通过指定边坡各节点摄动方向与大小的方式，分析了边坡水平与竖向位移场对弹性模量及泊松比的灵敏度.结果表明：单级边坡水平和竖向位移场对材料参数的灵敏度最敏感位置分别位于坡脚剪出口和坡顶后缘滑移面附近；相比弹性模量，边坡位移场对泊松比更为敏感；相比竖向位移场，边坡的水平位移场对材料参数更为敏感.

灵敏度分析；弹性模量；泊松比；土质边坡；位移场

灵敏度分析是利用系统中某些物理量的微分关系，来获得因变量对自变量敏感程度的方法.在岩土工程中，对研究对象、体系的某个或多个因子做灵敏度分析十分常见[1-2].此类分析可以找到对研究对象某方面贡献最大的因子，一般的做法是设计正交试验，通过控制变量的方式，改变某一参数或变量，以求得相应的系统响应量，进而分析其灵敏度.但是当涉及多因素分析时，工作量就显得繁琐且浩大，且对分析类似边坡位移场的灵敏度时，这样的方法还有其局限性.

前人对设计变量选取为岩土材料参数的灵敏度分析较多[3-4]，但这些研究都没有涉及边坡的位移场对岩土材料参数的灵敏度分析，本文采用基于Abaqus总位移法求解灵敏度的原理，对设计变量为弹性模量和泊松比进行了灵敏度分析，直接研究土坡变形对土体材料参数的灵敏度，找出对边坡位移场最大的影响因素与规律，以期对边坡的设计和施工提供借鉴和参考.

1 总位移法求解灵敏度的原理

本文采用的是在机械工程中应用较多的总位移法求解设计变量为材料参数时的灵敏度原理，并将其应用到岩土工程中.通过边坡各节点在指定方向上的微小改变（设计参数），求解出边坡位移场（设计响应）关于边坡形态变化的敏感度.设计响应对材料参数的灵敏度用总位移方法求解，设计响应 φr可以用式 φr= φr(uN(hp),hr)表示，则其对设计参数的灵敏度如式（1）所示.

式中： φr为设计响应， r = 1～ R，R为设计响应的数目； hp为设计参数， p = 1~P，P为设计参数的数目； uN为节点N的节点位移； uN(h )表示N节点的节点位移是关于设计参数的响应.为便于有

p限元求解，通过切线模量KNM进行转换，则有

式中： FM为节点N产生位移时在节点M的力.通过对式（2）与式（3）求解可得基于总位移法的设计响应关于材料参数的灵敏度，如弹性模量与泊松比等.

2 单级边坡

本文设计坡高10 m，坡顶宽度8 m，坡比 1 : 1的简单均质与非均质土坡采用摩尔库伦模型作为本构关系，均质土坡采用表1中土层I的土体参数；非均质土坡在红线以上部分采用表1中土层II的土体参数，红线以下部分采用表1中土层I的土体参数.在有限元Abaqus软件中，模型单元采用CPE4单元（平面四节点应变单元），模型尺寸与网格如图 1 所示.灵敏度命名遵循的规则是：d_ ｛response name｝_｛design parameter name｝，即d_U_E表示位移场U对弹性模量E的灵敏度.

表1 土坡材料参数

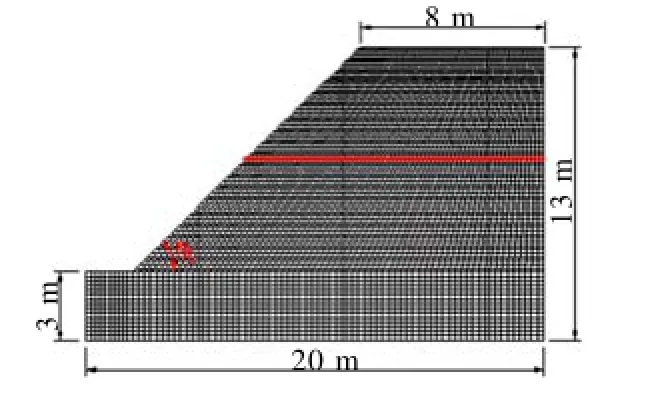
图1 边坡尺寸与有限元网格

2.1 均质边坡

在自重作用下，单级均质边坡的位移场如图2所示.所建模型的原点取在土坡的左下角，自重作用下位移偏向左下方，因此都为负值.计算采用摩尔库伦模型作为本构关系，潜在滑面较为明显.可以看到水平位移最大值为- 6 .6× 1 0-3m，出现在紧挨坡脚上方的滑面剪出口处；竖向位移最大值为- 1 .2× 1 0-2，出现在坡顶.

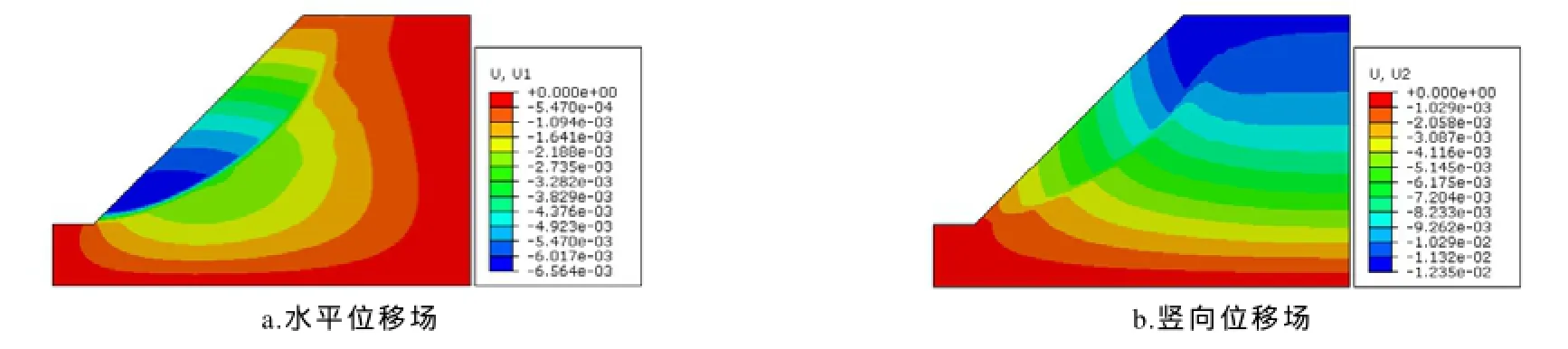
图2 均质边坡在自重作用下的位移场

对于单级均质边坡，其水平位移场对弹性模量的灵敏度最大值为 6 .6× 1 0-8，出现在紧挨坡脚滑面滑出口处上方，且灵敏度在滑面内沿坡面往上递减.竖向位移场对弹性模量的灵敏度最大值为1.2× 1 0-7，出现在坡顶，且在滑面出现错位，呈竖直向下递减.和图2位移场进行对比，灵敏度的最值与位移场最值出现部位基本一致，且最值的比值为弹性模量.

图3 均质边坡位移场对弹性模量的灵敏度

对于单级非均质边坡，其水平位移场对泊松比的灵敏度最大值为 1 .3× 1 0-2，出现在紧挨坡脚滑面剪出口上方和边坡土体中部，且灵敏度在滑面内沿坡面往上递减.且在滑面中部出现类似滑弧的带形最小负值区域，为- 2 .8× 1 0-2.竖向位移场对泊松比的灵敏度最大值为 5 .1× 1 0-2，出现在坡肩处和边坡土体中部，且灵敏度在滑面内沿坡面往下递减.对比同样可以得出，灵敏度最值的位置和位移场保持一致，且变化趋势大致相同.

图4 均质边坡位移场对泊松比的灵敏度

2.2 非均质边坡

在自重作用下，单级非均质边坡的位移场如图5所示.与均质土坡位移场相比，整个分布与变化趋势是一致的，非均质土坡的位移更大.具体来说，滑移体大小没有变化，但是单级非均质边坡在滑出口的水平位移更大，在坡顶的竖向右移也更大.

图 5 非均质边坡在自重作用下的位移场

对于单级非均质边坡，水平位移场对弹性模量的灵敏度最大值为 2 .7× 1 0-8，出现在滑面顶部与坡顶交汇处，且灵敏度在滑面内沿滑面往上递减，在边坡土体下部出现最小负值- 1 .6× 1 0-9.竖向位移场对弹性模量的灵敏度最大值也出现在滑面顶部与坡顶交汇处，值为 5 .2× 1 0-8，且灵敏度在滑面内沿滑面往下递减，在边坡土体下部出现最小负值- 1 .6× 1 0-9.与均质边坡相比，非均质边坡位移场更大，但是弹性模量的灵敏度更小.

图6 非均质边坡位移场对弹性模量的灵敏度

对于单级非均质边坡，水平位移场对泊松比的灵敏度最大值为 3 .2× 1 0-2，出现在滑面的中下部，且沿着坡面向上递减；最小值为- 3 .0× 1 0-3出现在滑面下端.竖向位移场对泊松比的灵敏度最大值出现在滑面入口与坡肩段，值为 2 .9× 1 0-2，且沿着坡面向下递减；最小负值为- 1 .3× 1 0-3出现在边坡底端.与均质边坡相比，非均质边坡位移场更大，但是水平位移场对泊松比的灵敏度非均质边坡更大，竖向位移场对泊松比的灵敏度均质边坡更大.同时对比位移场和灵敏度，两者的分布存在相似，这是由于灵敏度是位移场的偏导值.

图7 非均质边坡位移场对泊松比的灵敏度

3 归一化灵敏度对比

对材料参数进行归一化处理，结果如表2所示.由表2知，水平或竖向位移对弹性模量的灵敏度均比对泊松比的灵敏度小，这表明当单独减少或者增加弹性模量和泊松比时，改变泊松比所造成边坡水平位移场和竖向位移场的变化更大.此外，水平位移场对弹性模量和泊松比的灵敏度均高于竖向位移场，这说明边坡的水平位移场分布对弹性模量和泊松比更为敏感.

表2 归一化处理结果

4 结论

本文采用基于总位移法的灵敏度分析，对多因素灵敏度分析具有优势，但以上仅仅是对岩土参数的灵敏度等进行初步探索，后续可对边坡形态、抗剪强度甚至模态分析都可以进行研究.

[1]言志信，段建，蔡汉成，等.参数对岩石边坡稳定性的影响研究[J].西安建筑科技大学学报（自然科学版），2010,42(6):773-780.

[2]周勇，朱彦鹏.黄土地区框架预应力锚杆支护结构设计参数的灵敏度分析[J].岩石力学与工程学报，2006, 25(21):3115-3122.

[3]刘子振，言志信，凌松耀，等.非饱和土边坡抗剪强度的力学参数影响及灵敏度分析[J].中南大学学报（自然科学版），2012,43(11):4508-4513.

[4]郭立，马东霞，吴爱祥，等.岩体力学参数灵敏度分析的正交有限元法[J].中南大学学报（自然科学版），2004,35(1):138-141.

[责任编辑：韦 韬]

An Analysis of the Sensitivity of Slope Displacement Field to Elastic Modulus and Poisson’s Ratio

WANG Peng
(Hehai College,Chongqing Jiaotong University,Chongqing 400074,China)

This paper introduces the principle of using the ABAQUS total displacement method to resolve the sensitivity analysis where the design variables are the material parameters,constructs homogeneous and non-homogenous models for single-stage slopes using the Kulun model as the constitutive Moore,and analyses the sensitivity of slopes’horizontal and vertical displacement fields to elastic modulus and the Poisson’s ratio.The results show that the positions where single-stage horizontal and vertical displacement fields are most sensitive to material parameters are located near the shear crack at the foot of the slope and the slip surface at the top;compared with the elastic modulus,the slope displacement field is more sensitive to Poisson’s ratio;and compared with vertical displacement fields,the horizontal displacement field is more sensitive to the material parameters.

sensitivity analyses;elastic modulus;Poisson’s ratio;soil slopes;displacement fields

U416.1+4

A

1006-7302（2016）03-0040-04

2016-03-03

王鹏（1992—），男，重庆人，在读硕士生，研究方向为岩土工程.