双渠道供应链中广告横向合作策略研究

吴君（重庆交通大学 交通运输学院，重庆 400074）

双渠道供应链中广告横向合作策略研究

吴君
（重庆交通大学 交通运输学院，重庆 400074）

在网络零售商与传统零售商的双渠道供应链中，为了分析广告合作策略对双渠道需求与决策者利润的影响，采用 S tackelberg博弈法和Bertrand博弈法，建立了广告合作的双渠道模型，对比分析了不同博弈竞争下广告合作水平对渠道价格和渠道需求量的影响，以及各方利润与零售渠道偏好的关系.研究发现：网络零售商采取 Bertrand博弈时所获得利润大于进行Stackelberg博弈时所获得利润，传统零售商采取Stackelberg博弈时的最优利润是进行 B ertrand博弈获得利润的2倍.算例分析表明：进行广告合作后双方利润大幅提升，网络零售商利润与零售渠道偏好呈反向关系，传统零售商利润与零售渠道偏好呈正向关系.

双渠道供应链；Stackelberg博弈；Bertrand博弈；广告合作

随着网络的快速发展，网络零售商与传统零售商的竞争也越来越激烈，双方为增加渠道销量不断加大广告费用的投入，导致产品成本不断上升.若双方决策者愿意进行广告合作，不仅降低产品成本，还能缓解双渠道之间的竞争矛盾，如苏宁与阿里巴巴的合作策略.

赵礼强等[1]通过改进收入共享契约缓解制造商双渠道之间的冲突.YAO等[2-5]对比研究了在不同博弈下如何制定最优价格决策以及如何进行渠道选择.Chiang等[6-7]在双渠道供应链中分析了批发价与最优价格策略、最优利润之间的关系.孔庆山等[8-12]分析了服务水平、社会责任、广告投入、最优库存策略对决策者商定价与利润的影响.以上文献分析了其他因素以及在单一渠道中决策者如何制定价格策略.黄松等[13]分析了合作广告投入水平对渠道商定价决策与各方利润的影响.但以上文献没有考虑存在两个零售商时该如何进行广告合作.本文采用Stackelberg博弈和Bertrand博弈对比分析了不同博弈竞争下决策者进行广告合作时的最优利润.

1 学院基本模型与假设

1.1 问题描述

本文主要考虑制造商只经营批发，双渠道供应链包含1个网络零售商和1个传统零售商.广告的投入会增加渠道的需求量，假定两个零售商共同承担广告投入费用，从而降低渠道间的冲突，实现双方利润最大化，供应链系统模型如图1.

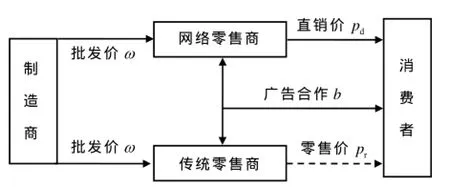
图1 广告横向合作的双渠道供应链模型

1.2 符号定义与模型假设

r：零售渠道；d：直销渠道.

a：市场对产品的基本需求；ρ：消费者对零售渠道偏好程度，且假设0 ＜ ρ＜ 1.

Dr：零售渠道需求量； Dd：直销渠道需求量.

α：渠道需求对本渠道价格的弹性系数；β：渠道需求对交叉价格的转移系数.

pr：零售价格，传统零售商决策变量； pd：直销价格，网络零售商决策变量.

kr：零售渠道广告投入的影响因子； kd：直销渠道广告投入的影响因子.

b：零售商在双渠道中总的广告投入水平，零售商决策变量，且b ∈ ( 0,)，其中为零售商准备投入广告的最大预算值.：广告投入对渠道需求的增加量， i = d,r.

为了简化分析，本文作以下假设：1）市场中存在两个零售商（网络零售商与传统零售商），假设双渠道供应链中不考虑制造商的影响.2）本渠道产品价格对本渠道需求量的影响更大，则假定0 ＜ 2β＜ α .3）网络渠道存在更多的潜在消费者，即 0 ＜ 2kr＜ kd.4）由于消费者对产品的价格更敏感，则假设价格对渠道需求量的影响大于广告对渠道需求量的影响，即 0＜ 2kr＜kd＜α.

由文献[14]的研究得知广告对渠道需求的作用是关于广告投入水平的增凹函数，根据文献[15]的研究构造出了线性需求函数，电子渠道需求（ Dd）和零售渠道需求（ Dr）分别为：

假定后文中的上标符号c表示集中式决策，上标s表示决策者们进行Stackelberg博弈，上标B表示决策者们进行Bertrand博弈.假定传统零售商愿意承担一定比例1-φ 的广告投入费用，因此网络零售商收益（ Πd）和传统零售商收益（ Πr）函数分别为：

渠道总利润：

2 不同决策模式下的定价策略

2.1 集中决策的双渠道供应链

双渠道供应链的最大化利润为：

命题1 当渠道总的广告投入水平b既定时，在双渠道供应链中采取集中式决策，电子渠道和零售渠道的最优价格（， p）策略为：

将式（7）、（8）代入式（5）中，此时渠道最优总利润为：

其中M =α/(4α2- 4 β2)， N = β/(2α2- 2β2)， X = a /(4α-4β)，Y= ［a( 1- 2ρ) ］ /(4α + 4β).在式（9）中通过对b求一阶偏导，令，则可以求得集中决策时最优广告策略b*.

2.2 分散决策的双渠道供应链

当网络零售商和传统零售商为了实现自身利润最大化而进行独立决策时，网络零售商和传统零售商将采用Stackelberg博弈和Bertrand博弈来制定定价策略.

2.2.1 Stackelberg博弈分析

Stackelberg博弈是经济学中的双寡头模型之一，即博弈中的两个竞争者分别是领导者和跟随者，领导者先对产品数量与价格进行选择，跟随者观察到领导者的选择后再做出选择.网络零售商在双渠道中的实力和主动权更强，因此双方将展开以网络零售商为主导的Stackelberg博弈.

命题2 实际上在网络零售商为主导的双渠道供应链中，大部分产品的网络直销价格 pd小于零售价格 pr，当时，网络零售商和传统零售商的渠道最优定价策略（，）为：

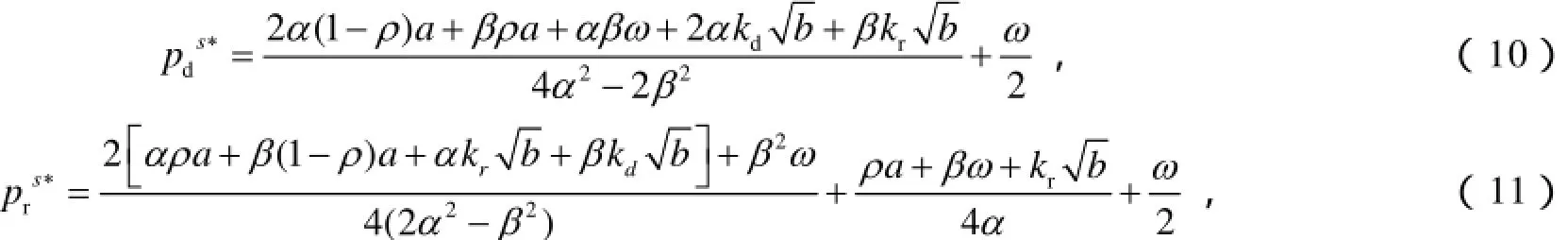
将式（10）、（11）分别代入式（3）、（4）中，化简后得到网络零售商和传统零售商的最优利润：

2.2.2 Bertrand博弈分析

Bertrand博弈是分析寡头垄断市场上价格竞争的模型，即假定市场中的竞争者同时生产相同的产品，同时定价，竞争者之间的产品具有完全替代性，则任何一个竞争者的最优定价策略不会以其他竞争者为主导，而只做出对其他竞争者定价的推测.如果网络零售商和传统零售商的实力相当，双方将以实现自身利润最大化为目的，而不以对方的价格决策为前提，因此双方将进行Bertrand博弈.

命题3 当网络零售商和传统零售商进行Bertrand博弈时，现实中仍然存在 pd≤ pr，则0 ＜≤时，双渠道的最优价格策略（，）为：

将式（14）、（15）分别代入式（3）、（4）中，化简后得到网络零售商和传统零售商的最优利润为：

只有当 0.5ρ＞ 时，这种竞争模式才存在，同理求得Bertrand博弈下的最优广告水平.

3 广告策略对双渠道影响的相关结论

为简化分析，假定制造商的批发价格ω为零.

结论1 在集中式决策的双渠道供应链中存在：

结论2 在进行Stackelberg博弈的双渠道供应链中有：

结论3 在进行Bertrand博弈的双渠道供应链中有：

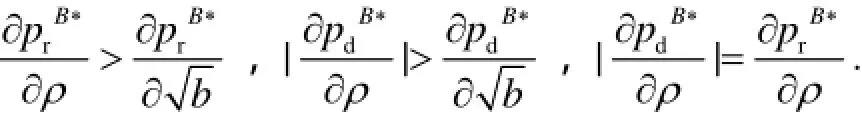
结论1至结论3表明：决策者们采用任何竞争模式，双渠道的价格和渠道的需求量都会随着广告投入的增加而增加.虽然渠道商投入广告后会产生一定的广告成本，但可以通过提高渠道的销售价格来弥补这一损失.在Bertrand博弈决策下，零售渠道偏好对销售价格的影响程度是一致的；在分散决策下零售价格关于参数ρ的变化率大于直销价格关于参数ρ的变化率.在Stackelberg博弈中由于网络零售商为主导者，当零售渠道发生变化时，网络零售商会首先做出反应，但此时网络零售商不知道传统零售商的决策，则不会大幅度改变直销价格.

结论4 在集中式双渠道供应链中有：

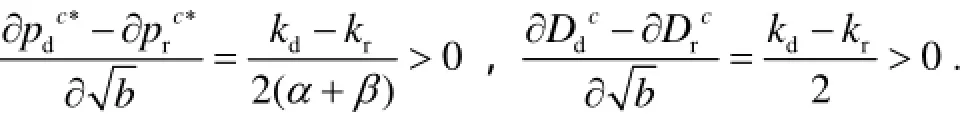
结论5 在Stackelberg竞争模式中有：

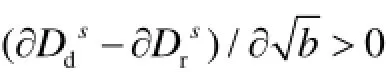
结论6 在Bertrand竞争模式中有：

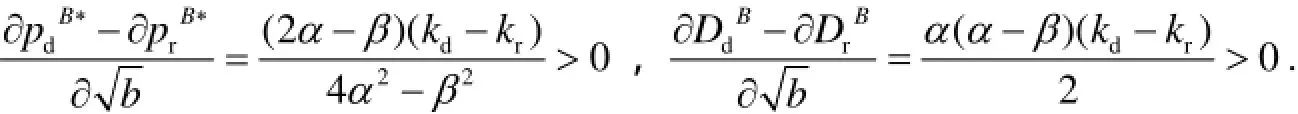
从结论4至6得知，当决策者们提高渠道广告投入时，不论决策者们采取何种竞争方式，网络渠道与零售渠道的价格和需求量都会增加，但网络渠道的价格和需求量的增幅始终大于传统零售渠道的价格与渠道需求量的增幅.

从结论7得知，Stackelberg博弈下广告水平对直销价格的促进作用大于Bertrand博弈，而广告水平对网络渠道需求量的促进作用却更小.这是因为在Stackelberg博弈中以网络零售商为主导，广告投入使得销售成本增加，为保证利润网络零售商开始大幅提高直销价格.但由于消费者对价格的敏感性，增长幅度越大，则抑制渠道需求量的幅度也会增大.同理，可以解释传统零售商进行Stackelberg博弈时广告水平对渠道价格的影响.

4 数值分析

首先分析在渠道商进行集中式决策时的双渠道供应链中，假定参数取值为： a = 200， kr= 1.3， kd= 2.7，b= 31， ω = 0，当参数 α = 6.5， β = 2.5时，，集中式供应链总利润函数是关于b的严格凹函数.当 α = 5.1， β = 2.5时，，此时供应链总利润函数是关于b的单调递增函数.当渠道偏好ρ在区间(0,1)上变化时，两种情况下的供应链最优价格策略与总利润如表1所示.当0 ＜ ρ ≤ 0.6时，渠道最优利润 πc*随着渠道偏好ρ的增加而减小，当0.6 ＜ ρ≤ 0.9时，渠道最优利润开始逐渐增加，但是始终没有渠道偏好ρ较小时的渠道最优利润大.这是因为随着网络的快速发展，网络零售商的实际销售成本比传统零售商的销售成本更低，未来传统零售商可能会逐渐向网络渠道转变.

表1 集中式双渠道供应链的最优价格策略与最优渠道总利润

保持其他参数不变的情况下，当传统零售商渠道偏好ρ在区间[0.51,0.9]上变化，网络零售商愿意承担的广告分担比例φ在区间(0.65,1)上变化时，分散式双渠道供应链的最优广告投入水平b*的变化趋势如图2所示.在Stackelberg博弈中，当 φ ∈ ( 0.65,0.7)时，随着零售渠道偏好的降低，广告投入水平反而大幅增加.这是由于在Stackelberg博弈中以网络零售商为主导者，从而刺激消费者购买，若广告的投入使顾客更加偏好网络渠道，则网络零售商就会不断增大广告投入.同理可以说明决策者们进行Bertrand博弈时的情况.

图2 不同博弈下分散式双渠道供应链的最优广告投入水平

从图3和图4可以得知，不论网络零售商进行何种博弈，网络零售商的最优利润都会随着零售渠道偏好ρ和广告分担比例φ的增加而减小，只有当参数ρ和φ都较小时，网络零售商的利润才最大，如图所示网络零售商更愿意采取Bertrand博弈.传统零售商采取Stackelberg博弈获得的最优利润是Bertrand博弈下的2倍，所以传统零售商更愿意采取Stackelberg博弈竞争.

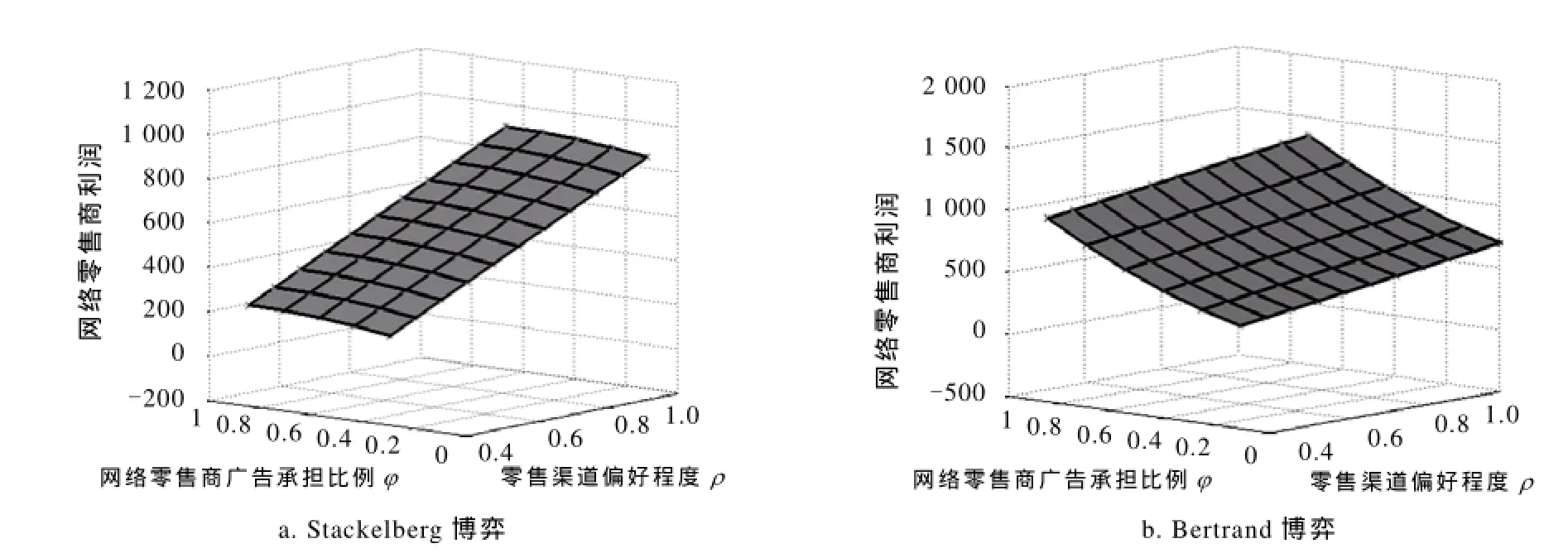
图3 不同博弈下分散式双渠道供应链网络零售商最优利润

图4 不同博弈下分散式双渠道供应链传统零售商最优利润

如图5所示，广告合作下的渠道商利润始终大于不进行广告合作下的利润，在任何博弈下双方进行广告合作后的利润与不进行广告合作的利润差额是一致的，在不同博弈竞争下进行广告合作双方获得的利润是不同的.

图5 不同博弈下渠道商利润与零售渠道偏好程度的关系

5 结论

本文建立了两个零售商之间广告合作的双渠道供应链模型，在不考虑制造商影响的情况下，用Stackelberg博弈法与Bertrand博弈法，对比分析了制造商与零售商在不同博弈下渠道销售价格、渠道需求量与零售渠道偏好程度、广告投入水平之间的关系.研究结论表明：1）在Stackelberg博弈下直销价格关于广告水平的变化率大于Bertrand博弈；且零售价格相反.2）在Stackelberg博弈下直销渠道需求量关于广告水平的变化率小于Bertrand博弈；且零售渠道需求量则相反.通过算例对比分析，发现传统零售商更愿意采取Stackelberg博弈，而网络零售商则愿意采取Bertrand博弈.

[1]赵礼强，徐家旺.基于电子市场的供应链双渠道冲突与协调的契约设计[J].中国管理科学，2014,22(5): 61-68.

[2]YAO Dongqing,LIU J J.Competitive pricing of mixed retail and e-tail distribution channels[J].Omega,2005, 33(3):235-247.

[3]YAN Ruiliang,PEI Zhi.Retail services and firm profit in a dual-channel market[J].Journal of Retailing and Consumer Services,2009,16(4):306-314.

[4]CAI G G,ZHANG Z G,ZHANG M.Game theoretical perspective on dual-channel supply chain competition with price discouns and price schemes[J].International Journal of Production Economics,2009,117(1):80-96.

[5]CAI G G.Channel selection and coordination in dual-channel supply chains[J].Journal of Retailing,2010, 86(1):22-36.

[6]CHIANG W K,CHHAJED D,HESS J D.Direct marketing,indirect profits:a strategic analysis of dual-channel supply-chain design[J].Management Science,2003,49(1):1-20.

[7]TSAY A A,AGRAWAL N.Channel conflict and coordination in the e-commerce age[J].Production and Operations Management,2004,13(1):93-110.

[8]孔庆山，刑伟，石晓梅，等.具有服务策略的双渠道供应链定价问题研究[J].商业研究，2012(5):114-118.

[9]XIE Jinying,WEI J C.Coordination advertising and pricing in a manufacturer-retailer channel[J].European Journal of Operational Research,2009,197(2):785-791.

[10]YU Yugang,HUANG G Q,LIANG Liang.Stackelberg game theoretical model for optimization advertising, pricing and inventory policies in vendor managed inventory production supply chains[J].Computers& Industrial Engineering,2009,57(1):368-382.

[11]YUE Jinfeng,AUSTIN J,WANG Minchiang,et al.Coordination of cooperative advertising in a two-level supply chain when manufacture offers discount[J].European Journal of Operational Research,2006,168(1): 65-85.

[12]黄松，杨超，张曦.双渠道供应链中定价与合作广告决策模型[J].计算机集成制造系统，2011,17(12): 2683-2692.

[13]黄松.双渠道供应链中定价与社会责任决策模型研究[J].商业研究，2014(5):153-161.

[14]YAO Dongqing,LIU J J.Competitive pricing of mixed retail and e-tail distribution channels[J].Omega,2005, 33:235-247.

[15]YU Yugang,HUANG G Q,LIANG Liang.Stackelberg game theoretical model for optimization advertising, pricing and inventory policies in vendor managed inventory production supply chains[J].Computers& Industrial Engineering,2009,57(1):368-382.

[责任编辑：韦 韬]

A Study of the Horizontal Cooperation Strategy for Advertising in Dual-channel Supply Chains

WU Jun
(College of Traffic&Transportation,Chongqing Jiaotong University,Chongqing 400074,China)

To study the influence of advertising cooperation strategy on demand of channel supply chain and the profit of decision-makers in the dual channel supply chain of online retailers and traditional retailers,a double channel model for advertising cooperation is established by adopting the Stackelberg game method and the Bertrand game method,the effect of advertising cooperation on channel price and demand and the relationship between the profits of parties and the preference of retail channels are compared and analyzed.The study finds that online retailers can achieve greater profits by adopting the Bertrand game method than by the Stackelberg method while traditional retailers’optimal profits by adopting the Stackelberg game method are twice of that by the Bertrand method.Example analysis shows:after adopting advertising cooperation,the profits of both sides increase substantially;there is a negative relationship between online retailers’profits and their retail channel preference and a positive relationship between traditional retailers’profits and their channel preference.

dual-channel supply chains;Stackelberg game;Bertrand game;advertising cooperation

F274

A

1006-7302（2016）03-0071-08

2016-02-26

吴君（1989—），男，重庆北碚人，在读硕士生，研究方向为运输经济与物流工程.