多控制点水平井靶体边界计算
2016-08-16冯小科汪松柏胡亚鹏张猛杜言平鲁港
冯小科汪松柏胡亚鹏张猛杜言平鲁港
1.中国石化河南石油工程有限公司;2.中国石油辽河油田勘探开发研究院
多控制点水平井靶体边界计算
冯小科1汪松柏1胡亚鹏1张猛1杜言平1鲁港2
1.中国石化河南石油工程有限公司;2.中国石油辽河油田勘探开发研究院
为在钻井设计软件中精确地绘制出多控制点水平井靶体,给出了多控制点水平井靶体的数学定义。以矢量代数为数学工具,利用靶体设计轴线上任意点的法面坐标,给出了靶体外边界曲线的数学定义,提出了曲边长方体靶的新概念,建立了靶体外边界曲线的计算公式。钻井设计软件开发实践及应用效果表明,曲边长方体靶的定义是合理的,计算公式是精确的,且易于编程实现;可以在水平投影图、垂直投影图、剖面展开图、三维图形中精确地绘制出水平井靶体图形。
钻井设计;水平井;井眼轨道;控制点;曲边长方体靶
最简单形状的水平井靶是一个长方体[1-3],由于空间直线向任意平面的投影仍然是直线(或退化成一点)[4],无论是水平投影图还是垂直投影图,可以很容易地画出长方体靶的投影图。当水平井需要通过多个目标点时,由于相邻2个目标点之间的设计轨迹可能是弯曲井段(例如空间圆弧),水平井靶外边界线(相当于长方体靶的与靶体轴线相平行的四条边)在水平(垂直)投影图上的投影不再是简单的直线段,而是复杂的三维连续曲线。对国内近20年来的文献进行检索,发现关于多控制点水平井靶体
1 长方体靶
Cuboid target
使用最多的水平井靶由2个控制点A和B所确定(参见图1),A点处靶窗矩形宽为2wA、高为2hA,其中±wA和±hA分别为A点的横向和纵向允许设计偏差。B点处靶窗矩形宽为2wB、高为2hB,其中±wB和±hb分别为B点的横向和纵向允许设计偏差。线段AB为设计井眼轨迹的一部分,称为靶体轴线。通常情况下,B点处的允许设计偏差可能会大于A点处的允许设计偏差,这时,靶体不再是长方体,而是截头方锥体[7]。

图1 水平井靶示意图Fig. 1 Target of horizontal well
刘修善等[1-2]考虑了地层倾角情况下的靶体摆放姿态。当地层倾角比较小时,总可以通过调整设计允许偏差的数值使得靶体位于目的层之内,而当地层倾角比较大时,也不太适合于设计成水平井,因此,工程上总是假定靶窗矩形的上、下边是与水平面相平行的。
对于靶体轴线上的任意点P,长方体靶的横截面仍然是一个矩形P1、P2、P3、P4,横向和纵向允许设计偏差由下式计算
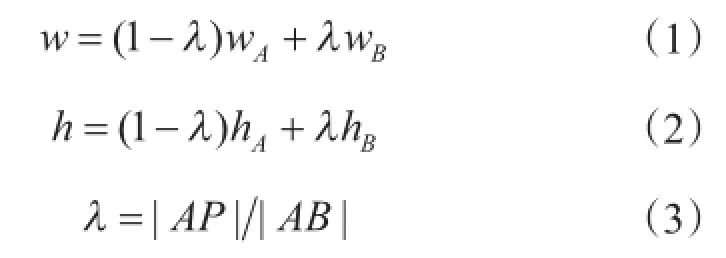
式中,具有长度量纲的参数其物理单位为m,角度的物理单位为rad。
当水平井靶体是由多个控制点所确定时,由于这些点不可能都在同一条直线上(否则只需要第一点和最后一点即可确定靶体),必定有某些相邻控制点之间的靶体轴线是曲线段(例如空间圆弧),这时,靶体不可能是简单的长方体或截头方锥体。
假想有一段截面为矩形空心钢管,柔性很好、不易折断,用手握住钢管两端用力使它弯曲,弯曲后的钢管的任意截面仍然为矩形。对这个假想实验进行数学抽象,建立多控制点水平井靶体的数学模型。
2 曲边长方体靶
Cuboid target with curved boundary
为具有几何直观性和计算公式简洁明了,采用矢量数学符号来进行相关计算公式的推导。
2.1井眼轨迹模型
Hole trajectory model
假设相邻2个控制点A和B之间的设计轨迹为一条三维空间曲线,井眼轨迹上任一点P的矢径可根据井深来计算

式中,r和rA分别为P点和A点的矢径(位置矢量);ΔL=L-LA为P点的井深增量(其中L和LA分别为P点和A点处井深);函数f(ΔL)为ΔL的连续可微矢量值函数。
由于井深L即是三维空间曲线的弧长参数,微分几何方法中的有关导数计算相对比较简单。
文中使用“列矢量”来表示矢量;上标“T”表示矩阵和矢量的转置运算,上撇符号“' ”表示对井深的一阶导数,“" ”表示对井深的二阶导数,‖‖表示矢量求模函数。
井眼方向矢量定义为井眼轨迹切线方向上的单位长度矢量

式中,t为井眼方向矢量,α为井斜角,φ为方位角。
主法线方向矢量和井眼曲率分别由下式计算

式中,n为主法线方向矢量,K为井眼曲率。
在井眼轨迹模型中,井斜角和方位角也能表示成井深或井深增量的函数

式中,函数g(ΔL)和h(ΔL)均为连续可微函数。矢径r有时也写成下面的形式

式中,函数F(α,φ,ΔL)为井斜角、方位角、井深增量的三元连续可微矢量值函数。
显然,将式(8)~(9)代入式(4)可知,矢径r仍然是井身L或井深增量ΔL的函数,井斜角变化率和方位角变化率分别由下式定义
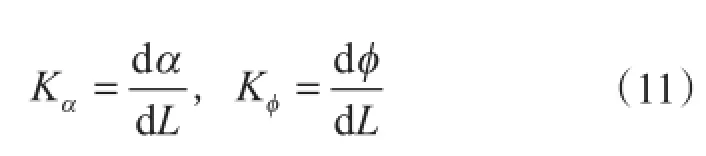
式中,Kα为井斜变化率,(°)/m;Kφ为方位变化率,(°)/m。
常用的井眼轨迹模型包括空间圆弧模型、圆柱螺线模型、自然曲线模型等[2],对于每一个具体的数学模型,都可以给出函数f、g、h、F的具体计算公式。
2.2井眼轨迹的法平面
Normal plane of hole trajectory
在设计井眼轨迹上任一点P,井眼高边矢量h和定向矢量v定义如下

可以证明[8]

式中,k=[0,0,1]T为垂直向下的单位长度矢量。
可以证明[8]:h、v、t是两两相互垂直的单位长度矢量,可以作为一个成右手系的空间直角坐标系的坐标轴上的单位长度矢量,这个坐标系称为P点的局部坐标系,参见图2。

图2 井眼轨迹的法平面Fig. 2 Normal plane of hole trajectory
假设Q点在局部坐标系中的位矢为ρ=(x,y,z)T,则

式中,q和p分别为Q点和P点在整体坐标系中的位矢,R为坐标变换矩阵,由下式计算[2,8]

由于矩阵R的单位正交矩阵,从式(16)得

2.3靶体轴线的伴随曲边长方体
Adjoint cuboid with curve border on the target’s axis line
对于靶体轴线(井眼设计轨迹从第一个控制点到最后一个控制点的那部分)上任意点P,按照式(1)~(2)定义该点的横向允许偏差w和纵向允许偏差h。在局部坐标系P-xyz中(见图3),矩形P1P2P3P4的中心为P点,宽和高分别为2 w和2 h。记矩形顶点Pi的局部坐标矢径依顺时针顺序为ρi=(xi,yi,0)T,i=1,2,3,4,则有ρ1=(h,w,0)T、ρ2= -(h,w,0)T、ρ3= (-h,-w,0)T、ρ4= (h,-w,0)T。

图3 局部坐标系Fig. 3 Local coordinate system
根据坐标变换公式(18),得到矩形顶点Pi在整体坐标系中的矢径

当井深L连续变化时,靶窗矩形所遍历的空间区域称为靶体轴线的伴随曲边长方体,简称曲边长方体。4个矩形顶点Pi形成4条连续曲线,称为曲边长方体的曲边,或简称边。
任意一条曲边曲线都不是简单的曲线,在一般情况下,既不是圆,也不是椭圆,甚至有可能不是平面曲线。
2.4曲边长方体靶
Cuboid target with curved boundary
当水平井靶由多个控制点所确定时,相邻2个控制点之间的靶体为截头方锥体(当两点之间设计井段为线段时),或者为曲边长方体(当两点之间设计井段为曲线时),将这些截头方锥体和/或曲边长方体按照控制点的顺序依次拼接,所形成的空间图形即为多控制点水平井段的设计靶体,称为曲边长方体靶。
如果相邻2个控制点之间由多个设计井段组成,可以将上段曲边长方体靶定义中的“控制点”改为“设计节点”,所形成的靶体仍为曲边长方体靶。
当靶体轴线的井眼曲率较小或者允许偏差较小时,曲边长方体靶是截头方锥体靶的合理推广。但是当井眼曲率大于允许偏差时,曲边长方体靶的“内侧”曲边会出现“折叠”现象。举例对曲边“折叠”现象加以解释。参见图4,4个控制点A、B、C、D均位于水平面上(垂深相等),横向允许偏差均为w,AB 和CD为线段,BC为圆弧,曲率半径为R。在情况(a)中, R=|BE|=|CE|>w,圆弧井段部分的曲边曲线均为圆弧曲线,属于正常情况;在情况(b)中,R=w,这时,圆弧井段部分的“内侧”曲边曲线退化成一个单独点;在情况(c)中,R<w,圆弧井段部分的“内侧”曲边曲线出现“折叠”现象。幸运的是,在工程实际中,极少出现这种极端现象。例如,取井眼曲率为K=30 (°)/30 m,则曲率半径R约等于57.3 m,而允许偏差一般不会达到这样大的数值。

图4 “折叠”现象的图解Fig. 4 Diagram for folding phenomenon
2.5井眼轨迹模型
Hole trajectory model
前面给出了曲边长方体靶的定义及有关计算公式。仔细分析上述定义可以发现,与特定井眼轨迹模型有关的参数只是矢径r、井眼方向矢量t、曲线主法线矢量n。所以,对于一般的靶体轴线曲线模型,只要能给出位矢、井斜角和方位角及其变化率的计算公式,就可以计算曲边长方体靶。
根据微分几何的知识[8],可推导出下式

这是刘修善公式[2]的矢量化形式。
另外,下式恒成立[2]

常用的井眼轨迹模型有空间圆弧模型[8]、圆柱螺线模型[2]、自然曲线模型[2]等,计算公式参见有关文献。对于恒工具面角模型[2]及样条曲线模型[2]等其他井眼轨迹模型,也均可以求出井斜角和方位角及其变化率公式、位矢公式。
3 绘图算法
Mapping algorithm
首先,依据设计井深增加的方向,根据式(19)等求出4条曲边上足够多的离散点,使得相邻2个离散点之间的直线距离足够小,当投影到计算机屏幕上时,这两点之间横/纵向不超过2个像素点。
如果是绘制三维图形,只需要分别将这些离散点用线段连接即可(当然还需要绘出第一个和最后一个控制点处的靶窗矩形)。
如果是绘制水平投影图,则离散点的Z坐标均相等,只需要绘制离散点(X,Y)即可。
如果是绘制垂直投影图,假设投影方位角为φ0,对每个离散点(X,Y,Z),计算视平移

绘图时绘制诸离散点(V,Z)。
如果是绘制剖面展开图,则需要利用靶体轴线的水平投影长度S和垂深Z的数据对(S,Z)。对于靶体轴线上任意点P,在该点的井眼高边矢量的正向和负向上各取一点P+和P-,它们与P点的距离均等于该点的纵向允许偏差,参见图5。
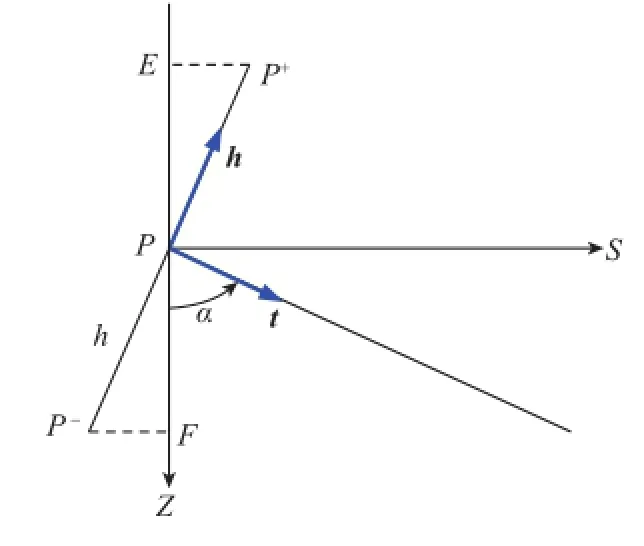
图5 剖面展开图参数计算示意图Fig. 5 Calculation sketch of unfolded section parameters
根据图5中的几何关系可求得

因此,在剖面展开图中,P±点在坐标为(s±hcosα,2±hsinα)。当P点沿圆弧从θ=0连续变动到θ=ε时,动点P+所形成的连续曲线和动点P-所形成的连续曲线可以作为曲边长方体在剖面展开图上的投影的上、下边界曲线。
4 算例
Case study
某多控制点水平井靶体设计参数见表1,设计井段AB为稳斜稳方位井段,BC和CD为空间圆弧井段,井眼曲率分别为8.90(°)/30 m和15.97(°)/30 m。使用文中算法绘制的水平投影图和垂直投影图(投影方位角63.43°)分别见图6和图7。

表1 控制点参数Table 1 Parameters of control points

图6 水平投影图Fig. 6 Horizontal projection
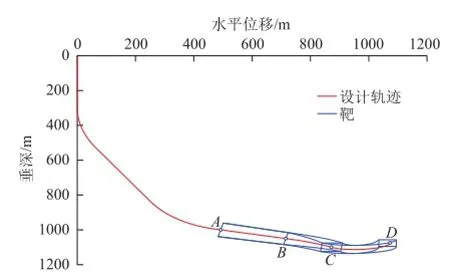
图7 垂直投影图Fig. 7 Vertical projection
5 结论
Conclusions
(1)利用法面坐标给出了多控制点水平井靶的外边界曲线的数学定义,推导出了设计轴线弯曲井段为空间圆弧曲线时的外边界曲线的具体计算公式,为钻井软件开发中的图形绘制提供了数学基础。
(2)软件开发实践表明,在水平投影图、垂直投影图、剖面展开图、三维图形中,使用外边界曲线公式可以绘制出多控制点水平井靶的精确图形。
References:
[1] 刘修善,王珊,贾仲宣,齐林,胡世军.井眼轨道设计理论与描述方法[M].哈尔滨:黑龙江科学技术出版社,1993:173-175. LIU Xiushan, WANG Shan, JIA Zhongxuan , QI Lin,HU Shijun. Wellbore trajectory design theory and Description method [M]. Harbin: Heilongjiang Science & Technology Press, 1993: 173-175.
[2] 刘修善.井眼轨道几何学[M].北京:石油工业出版社,2006: 76-80,127-152,180-183. LIU Xiushan. The geometry of wellbore trajectory[M]. Beijing: Petroleum Industry Press, 2006: 76-80, 127-152,180-183.
[3] 韩志勇.定向钻井设计与计算[M].东营:中国石油大学出版社,2007:141-142. HAN Zhiyong. Design and calculation of directional drilling[M]. Dongying: China University of Petroleum Press, 2007: 141-142.
[4] 苏步青,华宣积,忻元龙,张国樑.空间解析几何[M].上海:上海科学技术出版社,1984:78-101. SU Buqing, HUA Xuanji, XIN Yuanlong, ZHANG Guoliang. Space analytic geometry[M]. Shanghai: Shanghai Science & Technology Press, 1984: 78-101.
[5] 佟长海,常汉章,鲁港.多控制点水平井靶体参数的计算[J].天然气工业,2007,27(9):68-70. TONG Changhai, CHANG Hanzhang, LU Gang. Calculating parameters of horizontal well targets with multiple control points[J]. Natural Gas Industry, 2007,27(9): 68-70.
[6] 潭静.由三个控制点所确定的水平井靶的设计方法[J].江汉石油职工大学学报,2008,21(2):41-44. TAN Jing. Design methods of horizontal well targets determined by three control points[J]. Journal of Jianghan Petroleum University of Staff and Wordkers,2008, 21(2): 41-44.
[7] 《数学手册》编写组.数学手册[M].北京:人民教育出版社,1979:80,406-407. Compiling group of Handbook of Mathematics. Handbook of Mathematics[M]. Beijing: People's Education Press,1979: 80, 406-407.
[8] 鲁港,佟长海,夏泊洢,孙姝.空间圆弧轨迹的矢量描述技术[J].石油学报,2014,35(4):759-764. LU Gang, TONG Changhai, XIA Boyi, SUN Shu. Vector description of spatial-arc wellbore trajectory[J]. Acta Petrolei Sinica, 2014, 35(4): 759-764.
(修改稿收到日期 2016-03-22)
〔编辑 薛改珍〕
Calculation on the boundary of horizontal well target with multiple control points
FENG Xiaoke1, WANG Songbo1, HU Yapeng1, ZHANG Meng1, DU Yanping1, LU Gang2
1. SINOPEC He’ nan Petroleum Engineering Co. Ltd., Nanyang, Henan 473132, China;2. Exploration and Deνelopment Research Institute of PetroChina Liaohe Oilfield Company, Panjin, Liaoning 124010, China
The mathematical definition of horizontal well target with multiple control points was set, so as to describe it accurately in the drilling design software. The vector algebra was used as the mathematical tool, and the external boundary curve of target was mathematically defined by using the normal plane coordinates of an arbitrary point on the target design axis. Then, a new concept of cuboid target with curved boundary was proposed and the calculation formula was also established for the external boundary curve of target. And finally, the drilling design software was applied in field. It is shown that the definition of cuboid target with curved boundary is reasonable and its calculation formula is accurate and can be easily presented in programming. Moreover, it was made possible to draw horizontal well targets accurately in horizontal projection, vertical projection, profile expansion and 3D diagrams.
drilling design; horizontal well; hole trajectory; control point; cuboid target with curved boundary
鲁港(1963-),1985年毕业于复旦大学数学系应用数学专业,从事钻井工程数学模型和算法研究及计算机软件开发工作,高级工程师。通讯地址:(124010)辽宁省盘锦市兴隆台区石油大街95号。E-mail:Lugang1999@sina.com参数计算和绘图方面的研究论文几乎还是空白[5-6]。结合近年来的理论研究工作和钻井软件开发实践,笔者对多控制点水平井靶体参数计算和绘图的方法进行了一些理论总结。
TE21
A
1000 - 7393( 2016 ) 03 - 0286- 05
10.13639/j.odpt.2016.03.0002
FENG Xiaoke, WANG Songbo, HU Yapeng, ZHANG Meng, DU Yanping, LU Gang. Calculation on the boundary of horizontal well target with multiple control points[J]. Oil Drilling & Production Technology, 2016, 38(3): 286-290.
冯小科(1985-),2008年毕业于西安石油大学石油工程专业,长期从事钻井技术管理与研究工作,工程师。通讯地址:(473132)河南省南阳市河南石油工程有限公司。E-mail:214822882@qq.com
引用格式:冯小科,汪松柏,胡亚鹏,张猛,杜言平,鲁港.多控制点水平井靶体边界计算[J].石油钻采工艺,2016,38(3):286-290.
