MATLAB在控制系统时域分析中的应用

潘湘高, 杨民生, 敖章洪

MATLAB在控制系统时域分析中的应用

潘湘高, 杨民生, 敖章洪

(湖南文理学院 电气与信息工学院, 湖南 常德, 415000)

为了解决传统的控制系统时域分析法比较复杂和不能准确地求解三阶以上的高阶系统的问题, 将MATLAB控制系统工具箱和函数应用到控制系统时域分析中进行求解, 达到了既能快捷、准确地求出高阶系统的时间响应函数, 又能求出系统的时间响应波形和时域性能指标, 无需复杂的数学公式和数值计算。该方法简单直观, 极大地提高了对控制系统分析的精度和工作效率。

MATLAB控制系统; 时域分析; 阶跃响应; 脉冲响应

1　控制系统的时域分析

要对控制系统进行定量的分析就必须先建立数学模型。在时域分析法中, 经常要用到微分方程和传递函数以及动态结构图。然而时域分析法一般比较复杂[5-9], 公式很多, 对于高阶系统普通分析方法很难得到系统响应的时间函数表达式, 也很难准确地求出数值解和时域性能指标, MATLAB在控制系统时域分析中的应用能很好地解决这一难题。

1.1微分方程

线性系统的时域数学模型是线性微分方程, 设线性定常系统的微分方程为[5]

式(1)中, r(t)和c(t)分别为系统的输入、输出信号, 它们都是时间t的函数, 微分方程求解的过程比较麻烦,特别是对于高阶系统(n＞3)求解更加困难。

1.2传递函数

传递函数是控制系统复域数学模型, 是基于拉氏变换求解微分方程引出的, 在初值条件为0时对方程(1)两边进行拉氏变换(L)得

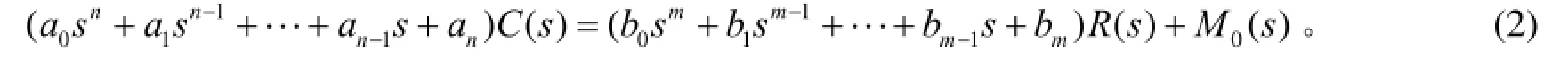
式(5)中,iA、jB、iC均为待定常数, 它们可用求极限的方法求出, 如等。

将式(5)进行拉氏反变换(L-1)得时间响应的表达式为

式(6)中前2项为零状态响应, 第3项为零输入响应。如果系统的初始状态都为0, 则式(2)中M0(s)=0, 由式(3)可得

式(8)中, 又可分为暂态响应(或暂态分量)和稳态响应(或稳态分量)。需要指出的是, 特征根 si在复平面的位置决定了系统的稳定性。只有当Re(si)＜0, 即系统稳定时, 式(6)中的第1项才能称为暂态响应, 所谓稳态响应一般是指强迫响应。

在对复变量s的代数式(分式)进行部分分式展开时, 例如由(4)式变为(5)式, 一般采用的方法, 首先求出代数式的所有极点si, 再将代数式写成部分分式形式, 最后根据的拉普拉斯反变换为, 可得

2　利用MATLAB求系统的时间响应

用普通数学方法求解高阶(3n＞)系统很困难, 而运用MATLAB命令或函数求解方便。执行命令num = [b0b1… bn], den = [1 a1… an]和[r, p, k] = residue(num, den)可求出C(s)/R(s)的部分分式展开式, 其中r、p 分别为各个部分分式的增益和极点位置, 而 k 为部分分式展开后的余项, 由 r、p、k 数值即可写出时间时响应函数表达式。

2.1传递函数为有理真分式形式

num = [1 2 6 10 24], den = [1 10 35 50 24]和[r, p, k] = residue(num, den) 3个命令执行后的结果为: r = -34.666 7, 37.500 0, -14.000 0, 3.166 7; p = -4.000 0, -3.000 0, -2.000 0, -1.000 0; k = 1。所以

当R(s) = 1 (即为单位脉冲输入)时, 可得到系统输出(单位脉冲响应)表达式为c(t) = -34.667e-4t+ 37.5e-3t- 14e-2t+ 3.166 7e-t+ δ(t); 当(即为单位阶跃输入)时,, 此时再执行命令: [r, p, k] = residue(num, [den 0])的结果为: r = 8.666 7, -12.500 0, 7.000 0, -3.166 7, 1.000 0; p = -4.000 0, -3.000 0, -2.000 0, -1.000 0, 0; k = [ ]。

由此得到的系统输出(单位阶跃响应)表达式为: c(t) = 8.666 7e-4t- 12.5e-3t+ 7e-2t- 3.166 7e-t+ 1, 系统的稳态响应为1。

2.2传递函数分子或分母为几个多项式相乘的形式

对遇函数分母多项式为乘积的形式, 要得到分母多项式的系数向量den, 可调用MATLAB函数conv( ), 以实现2个因式的乘积。执行个命令num = 4, den = [conv(conv([4 1], [1 4]), [2 3 1])]和[r, p, k] = residue(num, den)。结果r = -0.012 7, 0.444 4, -1.142 9, 0.711 1; p = -4.000 0, -1.000 0, -0.500 0, -0.250 0; k = [ ]。则当R(s) = 1时, 可得系统单位脉冲响应为: c(t) = -0.012 7e-4t+ 0.444 0e-t- 1.142 9e-0.5t+ 0.711 1e-0.25t。当(即为单位阶跃输入)时,, 此时再执行命令[r, p, k] = residue (num, [den 0])的结果为: r = 0.003 2, -0.444 4, 2.285 7, -2.844 4, 1.000 0; p = -4.000 0, -1.000 0, -0.500 0, -0.250 0, 0; k = [ ]。

由此可写出系统的单位阶跃响应为c(t) = 0.003 2e-4t- 0.444 4e-t+ 2.285 7e-0.5 t- 2.844 4 e-0.25 t+ 1。应当指出, 如果函数含有 m 重极点 p 的话, 则部分分式展开式包括。该形式对应的拉普拉斯反变换为:

2.3系统有正特征根的情况

系统1和系统2的脉冲响应和阶跃响应是收敛和稳定的, 而系统3的脉冲响应和斜坡响应都含有指数增长函数, 因此, 系统3不稳定。

2.4传递函数有复数极点情况

3　MATLAB在系统方框图化简中的应用

一个控制系统模型通常由一些典型环节按照基本连接结构相互连接构成, 而我们往往需要将比较复杂的系统化成简单的系统, 再进行分析与设计。在控制系统工具箱中提供了一些函数或命令来支持系统的连接和求解。命令G = tf(num, den)可建立系统的传递函数模型, 命令step(G), impulse(G)可分别求出系统的阶跃响应和脉冲响应。

图1　环节串联连接结构

3.1环节串联连接结构

环节串联连接如图1所示时, G(s) = G1(s) · G2(s), 可由MATLAB命令G=G1G2求出。

执行命令num1 = [1, 1]; den1 = conv([1, 0], [1, 1, 1]); G1= tf(num1, den1); num2 = [2, 3]; den2 =conv([1, 1], [1, 1]); G2= tf(num2, den2); G = G1*G2后的显示结果为

3.2环节并联连接结构

对图2所示的环节并联连接, G(s) = G1(s) ± G2(s)可由MATLAB命令G = G1± G2求出。

3.3反馈连接结构

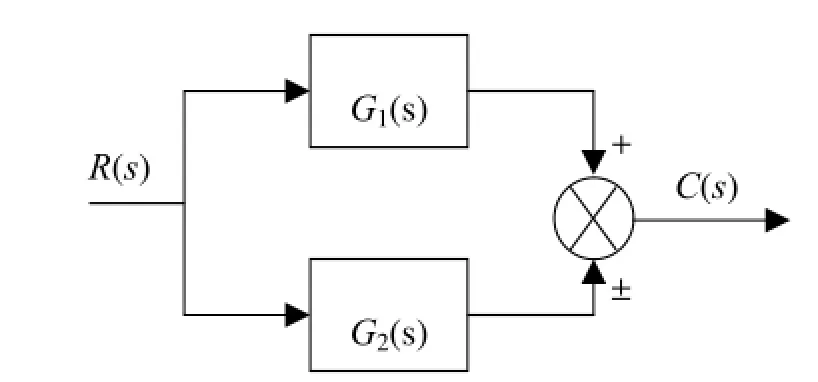
图2　环节并联连接结构

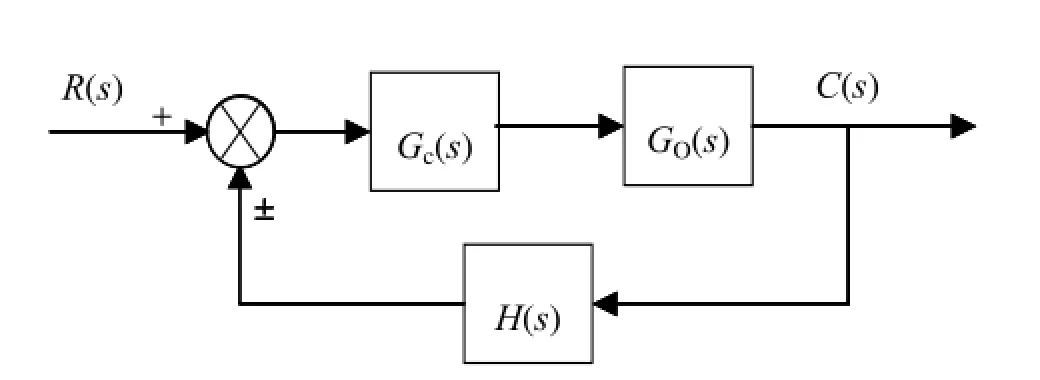
图3　反馈系统的方框图结构

4　利用MATLAB求闭环反馈控制系统的时间响应波形

num1 = [8 4]; den1 = [1 0]; Gc= tf(num1, den1); num2 = [1 2 4 24]; den2 = [1 0 25 40 24]; G0= tf(num2, den2); num3 = 1; den3 = [0.2 1]; H = tf(num3, den3); G1= GcG0; G = feedback(G1, H, -1)。结果为Transfer function:

用impulse(G)命令求得系统的单脉冲响应, 如图4所示; 用step(G)命令求得系统的单位阶跃响应[10],如图5所示。用鼠标点曲线上的任何一点即可显示该点的坐标数值, 故可非常方便地得到系统响应的时域性能指示[11], 由图5可见系统阶跃响应过渡过程振荡很据烈, 最大峰值为2.1, 峰值时间为1.15 s, 调节时间为34.2 s, 最大超调量为(2.1-1)/1 = 1.1 = 110%。系统的平稳性和快速性都很差, 至于如何改善系统的性能是系统校正设计的问题, 在此不再讨论。

图4　图3反馈控制系统的脉冲响应

图5　图3反馈控制系统的阶跃响应

5　结语

本文采用MALAB控制系统工具箱和函数对控制系统进行计算机辅助分析,

既能准确地求出高阶系统的时间响应函数, 也能求出系统的时间响应波形和时域性能指标, 无需复杂的数学公式和数值计算, 能极大地提高对控制系统分析的精度和工作效率, 解决了传统的控制系统时域分析法理论性强、抽象、涉及到数学知识多、难度大和不能准确求解三阶以上高阶系统的问题。

[1] 窦艳艳, 钱蕾, 冯金龙. 基于Matlab的模糊PID控制系统设计及仿真[J]. 电子科技, 2015, 28(2): 119-122.

[2] 谢云燕, 唐文亮, 梁来鹏. 基于MATLAB 的SVPWM逆变控制系统仿真[J]. 计算机系统应用, 2012, 21(1): 53-56.

[3] 胡寿松. 自动控制原理[M]. 6版. 北京: 科学出版社, 2013: 21-25.

[4] 姜伟, 谢诞梅, 陈畅, 等. 基于时域分析法的汽轮机末级叶片颤振预测及分析[J]. 振动与冲击, 2015, 34(11): 195-196.

[5] 陈怀琛. MATLAB在理工课程中的应用指南[M]. 西安: 西安电子科技大学出版社, 2005: 4-11.

[6] 骆建, 谢榕. 时域分析法的教学难点及应对方法[J]. 电气电子教学学报, 2015, 37(2): 55-56.

[7] 汪建. 用时域分析法求解冲激响应的方法[J]. 电气电子教学学报, 2011, 33(6): 103-104.

[8] 陈甜妹, 翁鹏浩, 彭茂兰, 等. 传输线时域响应格林函数分析法与数值拉普拉斯反变换方法的对比研究[J]. 现代电力, 2011, 28(5): 55-56.

[9] 秦艳. IP时域分析法的水轮机组控制系统数值计算[J]. 信息通信, 2016(1): 23-24.

[10] 黄忠霖, 黄京. 控制系统MATLAB计算及仿真[M]. 北京: 国防工业出版社, 2009: 12-15.

[11] 梁南丁, 赵永君. 自动控制原理与应用[M]. 北京: 北京大学出版社, 2007: 26-30.

(责任编校: 刘晓霞)

The application of MATLAB in control system time-domain analysis

Pan Xianggao, Yan Minsen, Ao Zhanghong
(College of Electrical and Information Engineering, Hunan University of Arts and Science, Changde 415000, China)

The traditional method of control system time-domain analysis which is very complicated cannot solve the problem of third order system or above accurately, when MATLAB control system toolbox and function is introduced into the control system analysis, the high order system time response function efficiently and accurately can be got. In the same time, the response waveform and time-domain performance index of the system can be got without complex mathematical formula and numerical calculation. This method is simple to manipulate, and it can greatly improve the precision of control system analysis and work efficiency.

MATLAB control system; time-domain analysis; step response; impulse response

TP 319

1672–6146(2016)03–0083–05

10.3969/j.issn.1672–6146.2016.03.018

潘湘高, 914868682@qq.com。

2016-06-10

湖南省科技厅资助项目(2012GK3123); 湖南省教育厅自动控制理论精品课程建设(湘教通[2015]332号)。

MATLAB语言是由美国的Clever Moler博士于1980 年开发的, 它是一种功能强大、内容丰富的计算机辅助设计软件。它特有的矩阵处理功能, 用于控制理论研究的专用工具箱和结构图程序设计的SIMULINK仿真环境, 使得MATLAB语言成为控制系统计算机辅助设计的有力工具[1]。文献[2]采用基于MATLAB的模糊PID控制器控制锅炉液位, 通过实验仿真比较传统PID控制、模糊控制以及模糊PID控制的效果。文献[3]介绍了在MATLAB环境下建立可调压、锁相的逆变控制系统, 模拟数字化EPS的变压、锁相环节。

传统的控制系统时域分析法[4]理论性比较强, 也比较抽象, 涉及到数学知识也较多, 难度比较大,特别是它不能准确求解三阶以上的高阶系统。针对以上问题, 本文采用MATLAB控制系统工具箱和函数对控制系统进行计算机辅助分析, 既能高效、快捷、准确地求出高阶系统的时间响应函数。同样地, 也能求出系统的时间响应波形和时域性能指标, 无需复杂的数学公式和数值计算, 能极大地提高了对控制系统分析的精度和工作效率。本文主要讨论MATLAB在控制系统时域分析中的应用。