高频谐振型静电除尘器控制技术

曹玲玲， 鲁建权， 杨民生， 王德玉

高频谐振型静电除尘器控制技术

曹玲玲， 鲁建权， 杨民生， 王德玉

（湖南文理学院 电气与信息工程学院， 湖南 常德， 415000）

分析了LCC谐振电源在电流断续模式下的双脉冲输出工作原理， 通过数学计算， 推导出了电路输出特性， 并在此基础之上完成了系统的小信号建模， 确定了系统闭环控制模型。通过优化数字PID参数， 提高了变换器的输出电压动态调节能力。搭建的1 700 V/200 mA实验室样机验证了除尘器电源控制模型的正确性和补偿器参数设计的合理性， 实现了除尘器输出电压的快速调节。

LCC谐振； 小信号建模； 闭环控制； 数字PID

1　LCC谐振电源工作原理

图 1为高频谐振型静电除尘电源拓扑主电路。其中： S1～S4为4只开关管， D1～D4为它们的反并联二极管； Lr为串联谐振电感， 它包含了变压器的漏感； Cs为外加串联谐振电容；Cp为并联谐振电容， 它包含了变压器匝间电容折算到原边的等效值； T为高频升压变压器，变比为1： n； D11～D14为输出整流二极管（高压硅堆）； Co、Ro为静电除尘器等效负载。Lr、Cs和Cp共同组成了LCC串并联谐振电路。

图1　LCC主电路原理图

1.1双脉冲输出工作原理

假设图1所示变换器工作在谐振电流断续模式下， Vin和Vo分别为输入和输出电压。开关管S1、S4或S2、S3开通前， 若Cp两端的电压已经达到钳位电压Ve， 其中Ve=Vo/n， 则称为双脉冲输出模式， 否则称为单脉冲输出模式。考虑到单脉冲输出的特性偏软， 在此基于双脉冲输出模式进行研究。

为了便于分析， 假设图1变换器中所有器件均为理想器件， 且输出滤波电容Co满足条件n2Cs，n2Cp， 变换器的主要工作过程可以分为4个阶段， 主要电路波形如图2所示。第1阶段（t0～t1）： t0时刻， 开关管S1、S4开通， Lr和Cs组成LC串联谐振， 谐振电流ir从0开始逐渐增大， 开关管实现零电流开通， 输出侧二极管D12、D13实现零电流导通， 能量向负载侧传递。第2阶段（t1～t2）： 谐振电流由0开始反向增大， 反并联二极管 D1、D4导通， 开关管 S1、S4实现零电流关断， 同时 Cp放电， 电压下降， 退出钳位， Lr、Cs、Cp组成LCC谐振， 输出侧二极管截止， 输出电压由Co提供。第3阶段（t2～t3）： t2时刻， 电容Cp电压已到达负的钳位电压-Ve， 电路再次转变为Lr和Cs构成的LC串联谐振，此时输出侧二极管 D11、D14自然导通， 能量再次向输出侧传递， 电流谐振至0时， D11、D14自然关断， 此阶段结束。第 4阶段（t3～t4）： 谐振电流保持为 0， 所有开关管均关断，无能量向负载侧传递， Vcp、Vcs保持不变。阶段4持续时间即电流断续时间。

图2　双脉冲模式电路主要波形

1.2双脉冲模式的电路特性

设sf为系统开关频率，ri为谐振电感Lr上流过的电流， 在双脉冲模式下， 若不考虑变换器内部的功率损耗， 即假设输出功率等于输入功率， 则可得到

设G0=Ve/Vin为电压增益， 由式（1）可得

因t2～t3阶段谐振电流ir为负值， 所以

因一个谐振周期总的电量为各个阶段充电电荷量之和， 即

由式（2）～（4）可得

（t0～t3）阶段， 对于串联谐振电容Cs有

（t1～t2）阶段， 对于并联谐振电容Cp有

第1阶段Cs的充电电荷为

整理得

1.3输出平均电流

由式（1）和式（6）可得到输出电流平均值Io的表达式为

2　系统建模及闭环控制

以 LCC电路工作在电流断续双脉冲工作模式下的电路数学分析为基础， 建立系统的小信号模型，并在此基础之上实现系统的闭环控制。

2.1小信号建模

设oCi为流过输出电容Co的电流，oRi为流过输出电阻Ro的电流， io为总的输出电流， 则对负载侧应用基尔霍夫电流公式有

将式（9）和式（10）代入（11）得

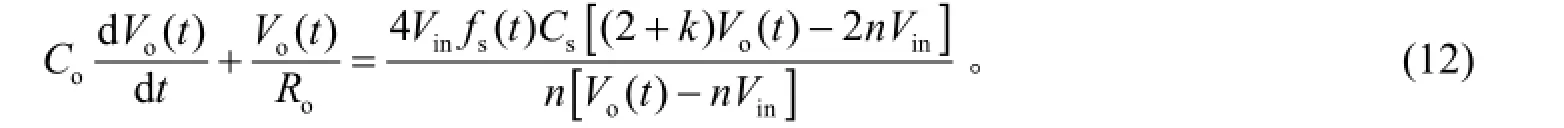
如果对输出电压Vo（t）和开关频率fs（t）在稳态工作点Vo、Fs附近作微小的扰动， 即

将式（13）、（14）代入式（12）得

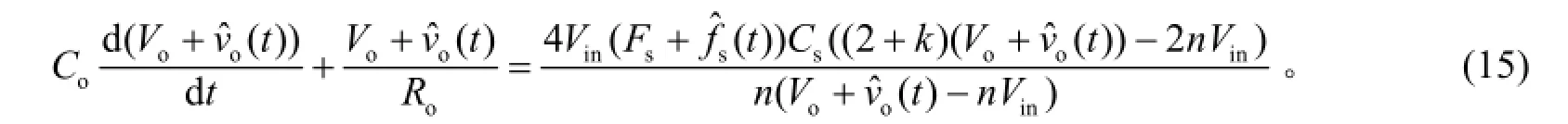
由于输出电压Vo为常数， 因此其倒数为0， 式（15）整理得

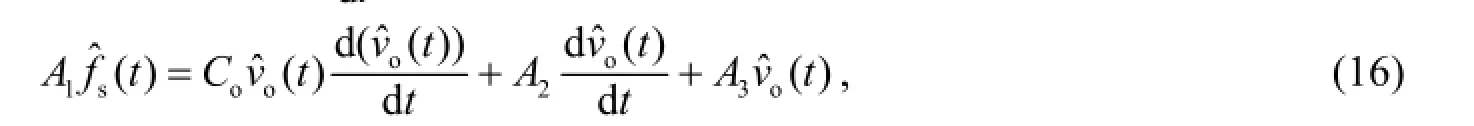
对式（17）进行拉氏变换， 得到系统控制量与输出量之间的关系式

2.2闭环控制

LCC变换器闭环系统框图如图3所示。其中：Vref（s）为给定电压； Gc（s）为待设计的补偿网络的传递函数； Gef（s）为电压到频率的传递函数； Gfv（s）为频率到输出电压的传递函数； H（s）为反馈分压网络的传递函数。

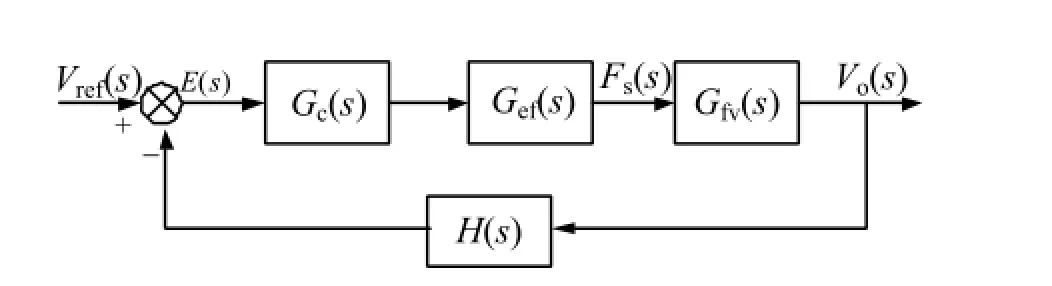
图3　LCC闭环系统框图

将额定点各变量参数Vin= 250 V， Vo=1 700 V， Cp= 60 nF， Cs= 0.225 μF， n = 20， Fs= 9.3 kHz， 代入A1、A2、A3表达式可得本实验系统频率到输出的传递函数

未加入补偿环节时， 系统原始回路增益函数为

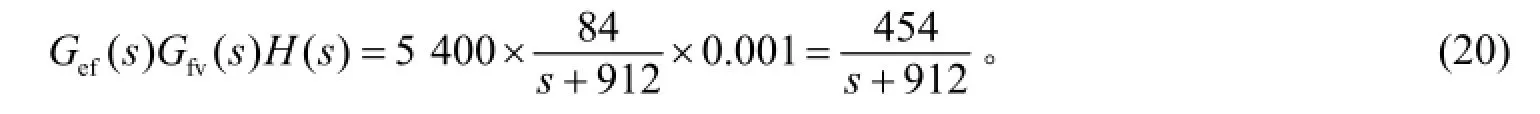
补偿环节Gc（s）采用PI比例积分环节， 通常希望加入补偿环节后的传递函数为

2.3数字化PI控制

在工业控制系统中， PID调节器由于其具有结构简单、参数容易调整等优点， 是应用最广泛的控制器。它通过计算给定值与被控量的偏差， 并对偏差值分别进行比例、积分和微分运算， 从而得到系统控制量。调节比例、积分和微分3个参数就可使系统获得良好的控制性能。将式（22）离散化， 可得数字PID参数： Kp= 4.1， KI= 0.25， KD= 0。

3　系统实验

图4为给定Vref= 1 700 V， KI= 0， Kp由小到大的响应曲线， 其中输出电压测量衰减1 000倍。分析可知， Kp= 4时， 响应最快， 一次脉动即进入稳态值1 470 V， 系统过渡时间6 ms。系统存在系统静差， 需加入积分环节。

图5为给定Vref= 1 700 V， Kp= 4， 不同KI时的阶跃信号响应曲线。可以看出Kp= 4， KI= 0.2时， Vo= 1 700 V， 首次峰值Vmax= 2 400 V， 且过渡时间ts= 12 ms， 2次脉动即可达到稳态值， 满足系统要求， 阶跃响应迅速， 超调较小， 无静差， 具有良好的动态响应和稳态值。

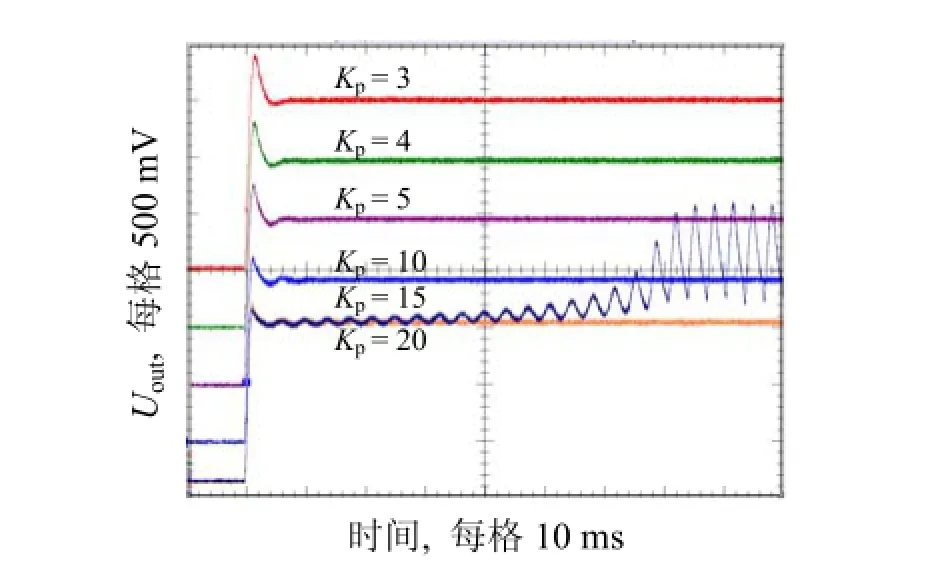
图4　Kp不同时的阶跃响应曲线

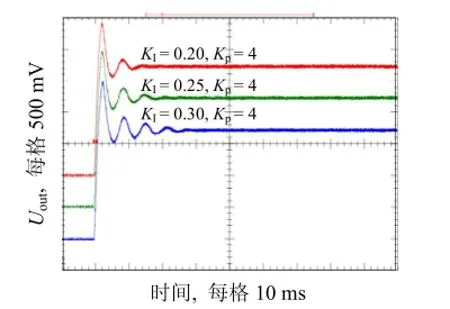
图5　KI不同时的阶跃响应曲线

4　结论

本文对高频LCC电源断流模式下的双脉冲工作模式进行了深入研究， 建立了系统的控制到输出小信号模型传递函数， 为了方便控制器的参数设计， 进一步将其化简为一阶惯性环节。基于该模型， 通过频域分析设计了补偿器环节， 并利用DSP实现对输出电压的闭环控制。通过优化比例系数降低动态响应时间， 再进一步加入积分系数来消除稳态静差。本文通过构建的1 700 V / 200 mA原理样机实验， 验证了LCC谐振变换器的电压输出调解能力： 输出电压动态超调较小、稳态无静差。在启动过程中， 其阶跃响应过渡时间仅有12 ms， 远远低于传统工频除尘器100 ms以上的动态响应指标， 为静电除尘器工作在负载闪络条件下， 实现最佳闪络率控制奠定基础。基于本文中对电压输出特性的提升， 作者将在下一步工作中将闪络率控制算法引入到LCC高频静电除尘变换器的DSP控制系统当中， 从而显著改善整个系统的除尘效率。

［1］ GB 1223-2011. 火电厂大气污染排放标准［S］.

［2］ 熊桂龙， 李水清， 陈晟. 增强PM2.5脱除的新型电除尘技术的发展［J］. 中国电机工程学报， 2015， 35（9）： 2 217-2 223. ［3］ 章志昕， 叶青， 来佳磊. 高频电源在静电除尘器上的应用［J］. 发电技术， 2016， 35（1）： 57-60.

［4］ 殷召伟， 宋刚， 盛乾. 电除尘用新型高频脉冲电源［J］. 自动化应用， 2014（7）： 117-118.

［5］ 刘军， 官威， 石健将. 高压静电除尘用电源调压特性的分析［J］. 高电压技术， 2009， 35（2）： 344-348.

［6］ Slobodan Vukosavic， Nikola Popov， Zeljko Despotovic. Power electronics solution to dust emissions from thermal power plants ［J］. Serblan Journal of Electrical Engineering， 2010， 7（2）： 231-252.

［7］ Thiago Soeiro， Jurgen Biela， Jonas Muhlethaler. Optimal design of resonant converter for electrostatic precipitators ［C］// International Power Electonics Conference， 2010： 2 294-2 230.

［8］ Grass Norbert. Electrostatic precipitator diagnostics based on flashover characteristics［J］. IEEE Industry Applications Society， 2005（4）： 2 573-2 577.

［9］ Grass Norbert. Electrostatic precipitator control systems ［J］. IEEE Industry Applications Magazine， 2010， 16（4）： 28-33.

［10］ Hu Manli， Fröhleke Norbert， Böcker Joachim. Small-signal model and control design of LCC resonant converter with a capacitive load applied in very low frequency high voltage test system ［C］// 2009 IEEE Energy Conversion Congress and Exposition， 2009： 2 972-2 979.

（责任编校： 刘晓霞）

Control technology of ESP with high frequency resonant converter

Cao Lingling， Lu Jianquan， Yang Minsheng， Wang Deyu
（College of Electrical and Information Engineering， Hunan University of Arts and Science， Changde 415000， China）

The working principle of double pulses output mode of LCC resonant power supply in DCM is analyzed. The output characteristics of the circuit are derived by mathematical calculations， and the system small signal model is provided， also the system’s closed-loop control model is given. The dynamic nature of the output voltage of the converter is improved by the optimized numerical PID configures. The validity of the control model and the rationality of the compensator configure design are verified by the 1 700 V/200 mA experimental prototype， and the rapid adjustment of the ESP’s output voltage is realized.

LCC resonant； small signal model； closed-loop control； numerical PID

TM 925.31

1672-6146（2016）03-0071-05

10.3969/j.issn.1672-6146.2016.03.015

曹玲玲， 5569014@qq.com。

2016-06-08

湖南省教育厅一般项目（14C0787）； 湖南省自然科学基金常德地区项目（13JJ9023）。参数， 提高除尘器设备的输出电压调节能力， 为实现静电除尘器负载的闪络控制奠定基础。

近年来， 我国连续多次遭受大范围的重度雾霾天气， 其根本原因是大气污染物排放量大。2011年7月环境保护部与国家质量监督检验检疫总局下发了最新的《火电厂大气污染物排放标准》［1］， 其中规定现有火电厂与新建火电厂的烟尘排放标准从2004年的50 mg/m3降低到30 mg/m3。为了减少工业生产中粉尘的排放量， 可以采用各种除尘装置［2-4］。其中高频谐振型静电除尘器因其具有除尘效率高、能耗小、体积小、运行费用低等优点， 在工业除尘领域得到越来越广泛的应用［5-7］。

除尘效率是衡量除尘器性能优劣的重要指标， 在除尘的过程中需要尽量提高除尘器输出电压以保证高除尘率， 因此两极间的闪络放电现象不可避免。但过于频繁的闪络发生不仅会降低除尘率和电效率，而且对除尘器本体也会造成严重损害。因此提高静电除尘器的供电电源特性和对负载闪络进行有效控制， 对除尘效率的提高具有重要意义。目前针对静电除尘器的动态输出特性研究的相关文章很少， 仅有少量文章对于传统的工频静电除尘器的应对闪络现象的弊端和高频变换器的优势进行了探讨［8-10］。本文针对高频LCC谐振型变换器的建模及控制技术展开研究， 分析了谐振电流断续模式下LCC谐振变换器的工作原理， 区分单脉冲输出和双脉冲输出2种不同工作模式， 推导了双脉冲输出模式下状态变量的表达式， 进而建立LCC变换器的控制量与输出量之间的数学模型。通过优化基于DSP的数字PI控制