图像去噪中LLT模型的同伦方法

杨奋林, 郭二冬(吉首大学 数学与统计学院, 湖南 吉首, 416000)

图像去噪中LLT模型的同伦方法

杨奋林, 郭二冬
(吉首大学 数学与统计学院, 湖南 吉首, 416000)

提出了运用具有全局收敛性的同伦方法求解 Lysaker-Lundervold-Tai (LLT)模型, 构造了一种逐步减小光滑化参数的同伦方程, 并给出了有效的路径跟踪方法。实验表明, 该方法收敛速度是不动点方法的2倍。

图像去噪; LLT模型; 不动点方法; 同伦方法

自Rudin等[1]提出TV模型以来, 基于变分偏微分方程的图像处理技术得到迅速发展。该技术结合了图像的本质特征, 是目前图像恢复中能够保持图像边缘的有效方法之一[2–6]。该技术已广泛应用于图像去噪、图像分割、图像修补、图像配准等多个领域。Lysaker等[7]提出的LLT模型是一种能够有效抑制TV模型阶梯效应, 保持图像光滑的高阶变分模型。该模型在医学核磁图像处理中得到很好的应用。由于该模型的高度非线性性和奇异性, 求解十分困难。目前主要的求解方法有人工时间演化方法、不动点方法、非线性多重网格方法[8–9]和非光滑牛顿法[2]。牛顿法求解非线性问题具有二阶收敛性, 由于该方法对初值要求苛刻, 以观察图像作为初值该方法不收敛, 本文考虑运用具有大范围收敛性的同伦方法求解LLT模型[10–11]。

1　LLT模型

二阶泛函做正则化项的LLT模型[7]:, 这里z为已知的观察图像, u为原始图像, Ω是有界凸集, 通常取, 其中或。为了叙述方便, 本文以为例对同伦方法进行描述。

该变分模型的求解通常转化为求解能量泛函的最优性条件, 即Euler-Lagrange方程

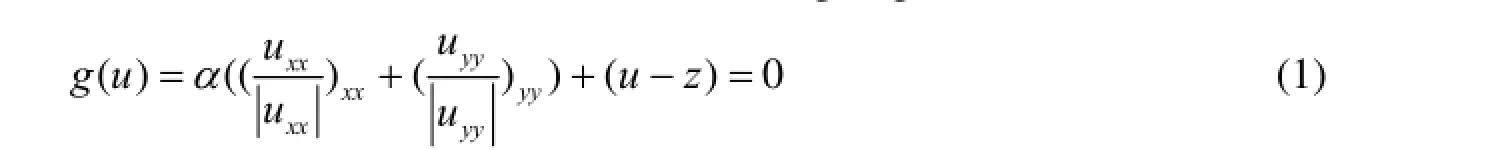
由于 Euler-Lagrange方程(1)的奇异性和非线性性程度很高, 人工时间演化方法和不动点方法求解收敛比较困难, 速度非常慢, 而具有二阶收敛性的牛顿法, 由于其收敛域很小, 选初值非常困难而没法工作, 因此, 本文考虑运用具有全局收敛性的同伦方法来求解方程(1)。

2　同伦方程

同伦方法是具有全局收敛性的一类求解非线性问题的方法[5], 注意到当光滑化参数β很大时, 方程(1)的非线性程度低, 容易求解, 因此, 考虑构造随着t从0增加到1而光滑化参数逐步减小的同伦方程:

当t = 0时, H(u, 0) = u – z = 0为线性方程。

光滑化参数β + (1 - t)/t2随着t的增大而减小, 对应方程的非线性程度增加。当t = 1时, H(u, 1) = g(u) = 0为所求的Euler-Lagrange方程(1)。

3　路径跟踪

路径跟踪实际上就是跟踪H(u, t) = 0的解曲线, 该过程由预估和校正2部分交替完成。由于H(u, 0) = u - z = 0的解为观察图像z, H(u, t) = 0的非线性程度随着t的增大而增加, 考虑t自适应从0增加到1,跟踪过程即求解一列H(u, tk) = 0, 每次预估采用前一步校正值做为预估值, 也就是下一步的校正初值。校正过程采用不动点方法求解H(u, tk) = 0。路径跟踪的具体过程如下。

步1, 给定初值。令k = 1, u0= z, t0= 0, 初始步长为h。

步2, 预估。令tk= tk-1+ min(h, 1 - tk-1), 如果tk= 1, 以uk-1做为不动点迭代初值, 运用不动点方法求解H(u, tk) = 0, 得uk, 即Euler-Lagrange方程的解。否则, 转步3。

步3, 校正。以uk-1做为不动点迭代初值, 运用不动点方法求解H(u, tk) = 0, 得uk, 并记录迭代次数,并令k = k + 1。

步4. 调节步长。如果校正步数不超过3, 增大步长; 如果校正步数大于6, 减小步长, 转步2。

4　数值实验

实验图像是像素为128 × 128的triangular图像(图1), 以绝对残量减少至10-4为终止条件。

图1　实验图像

表1列出了β取不同的值时, 不动点方法所需的迭代次数和时间。从表1可以看出, 随着β的减小, 迭代次数显著增多, 运算时间增大。

在β = 10-9、10-10、10-12时, 比较不动点方法和同伦方法的收敛速度。表2列出了2种方法总迭代次数和所用时间。表2显示, 不动点方法总的迭代次数和所用时间大约为同伦方法的2倍。

表1　β取不同值时, 以z为初值的不动点迭代次数和花费的时间

表2　β取不同值时, 不动点方法和同伦方法的总迭代次数和花费的时间

5　结论

LLT模型是图像去噪中能够抑制阶梯效应保持图像光滑的一类重要高阶变分模型。针对LLT模型的求解问题, 本文提出运用逐步延拓光滑化参数的同伦方法求解Euler-Lagrange方程(1), 并设计了有效的路径跟踪方法。数值实验表明同伦方法不仅能有效求解Euler-Lagrange方程(1), 而且收敛速度是不动点方法的2倍。

[1] Rudin L, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms [J]. Physica D, 1992, 60(1): 259–268.

[2] 庞志峰. 图像去噪问题中的几类非光滑数值方法[D]. 长沙: 湖南大学, 2010.

[3] 张建平. 基于偏微分方程的图像去噪和分割方法[D]. 大连: 大连理工大学, 2012.

[4] Chan T F, Shen J H. Image processing and analysis-variational, PDE, wavelet, and stochastic methods [M]. Philadelphia: SIAM Publications, 2005: 1–5.

[5] 吴斌, 吴亚东, 张红英. 基于变分偏微分方程的图像复原技术[M]. 北京: 北京大学出版社, 2008: 10–17.

[6] 肖林, 严慧玲, 周文辉. 求解二次规划问题的快速收敛梯度神经网络模型设计及仿真[J]. 湖南文理学院学报(自然科学版), 2016, 28(1): 51–54.

[7] Lysaker M, Lundervold A, Tai X C. Noise removal using fourth-order partial differential equation with applications to medical magnetic resonance images in space and time [J]. IEEE Trans Image Process, 2003, 12(12): 1 579–1 590.

[8] Carlos Brito-Loeza, Chen Ke. Multigrid algorithm for high order denoising [J]. SIAM J Image Sci, 2010, 3(3): 363–389.

[9] Chang Qianshun, Chern I. Acceleration methods for total variation-based image denoising [J]. SIAM J Sci Comput, 2003, 25(3): 983–994.

[10] 王则柯. 同伦方法引论[M]. 重庆: 重庆出版社, 2011: 9–11.

[11] Yang Fenlin, Chen Ke, Yu Bo. Efficient homotopy solution and a convex combination of ROF and LLT models for image restoration [J]. International Journal of Numerical Analysis and Modeling, 2012, 9(4): 907–927.

(责任编校: 刘刚毅)P

Homotopy method for LLT model in image denoising

Yang Fenlin, Guo Erdong
(College of Mathematics and Statistics, Jishou University, Jishou 416000, China)

A homotopy method which has globally convergence is used to solve the LLT model in this paper. A homotopy equation is constructed by gradually reducing the smooth parameter, and then an efficient curve tracking is given for solving this equation. Numerical tests show the convergence of this method is more than two times for the fixed point method.

image denoising; LLT model; fixed point method; homotopy method

TB 115.1

1672–6146(2016)03–0076–03

10.3969/j.issn.1672–6146.2016.03.016

杨奋林, 478002158@qq.com。

2016–04–18

国家自然科学基金(11501243)。