小波变换在医学图像处理中的应用

尚珍　聂泽花

摘 要： 利用小波变换的理论分析对近年来小波变换在医学图像处理方面的应用进行综述并分析其局限性。如：一阶导数小波函数图像的边缘提取；利用小波变换进行图像分解以提高信噪比；基于小波变换对图像通过低频分解系数进行增强处理；小波变换在医学图像压缩中局部信号的处理；基于小波的图像融合等。提出小波变换与其他技术的综合应用是远程医学图像传输的发展趋势。

关键词： 小波变换； 图像处理； 局限性； 改进方法

中图分类号：TP391 文献标志码：A 文章编号：1006-8228（2016）08-56-04

Abstract： The application of wavelet transform in medical image processing is reviewed and the limitation is analyzed in this paper. Such as first-order derivative wavelet function image edge extraction； image decomposing with wavelet transform to improve the signal-to-noise ratio； image enhancement processing with low frequency decomposition coefficient based on wavelet transform； using wavelet transform to process the local signals in medical image compression； the image fusion method based on wavelet etc. It is proposed that the comprehensive application of wavelet transform and other technologies is the development trend of remote medical image transmission.

Key words： wavelet transform； image processing； limitation； improvement method

0 引言

在医学技术的发展中，医学影像技术无疑成为其中一个重要分支，其发展使医生能直接观察到人体内部病变的部位，确诊率提高。医学图像采集与图像后处理成为衡量医学影像技术水平的标志之一，图像变换的处理思维和处理方法是一个涉及多学科的焦点问题，图像变换将空间域中表达的图像转换到变换域后，利用变换域中的特定方法对其进行处理[1]。采用图像变换的好处至少可归结为两个：①在变换域中的某些处理手段与滤波相联系，过程直观；②利用变换能够简化计算或作某种特殊应用，处理方便。因此就应用角度而言，傅里叶变换（Fourier transform）、离散余弦变换（Discrete cosine transform）和小波变换（Wavelet transform）可以将图像变换看作是简化问题求解的一种技巧，图像变换被广泛运用于图像特征提取、图像增强、图像压缩和图像识别等领域。但小波变换在图像处理中可达到独有的效果，特别是在医学局部性病灶的影像图像分析中优势明显，本文综述其在医学图像处理中的应用。

1 小波变换在医学图像处理中的应用

小波和小波变换的概念是在20世纪70年代首先提出的，小波变换的思想源于伸缩和平移方法。如果函数满足[2]：

为函数经伸缩和平移得到的小波函数族。其中a，b为伸缩和平移因子。

与Fourier变换相比而言，它解决了Fourier变换中许多不能解决的问题，同时也继承了傅里叶变换[3]局部化思想，克服了窗口大小不随频率变化的特点，提供一个随频率改变的时间-频率窗口[4]，同时小波变换因其突出的时频变换特性和小波基函数选择的灵活性，在医学图像处理中获得了广泛的应用。

1.1 小波变换在医学图像压缩中的应用

目前，医学图像数据常采用的压缩方法主要有RLG、JPEG，这两种压缩方法均有其固有缺陷。RLG方法适用于数据相关性非常高的医学图像压缩，JPEG方法使用时会使图像有局部马赛克反应。在医学图像压缩方法中使用小波变换，重点是对图像中局部信号的提取处理。

系数编码是小波变换用于压缩的核心，压缩的实质是对系数的量化压缩。图像能量主要集中在少数低频系数上，因此对低频系数精细量化，而对高频系数粗糙量化甚至完全抛弃，可达到减少表示像素所需平均比特数的目的。与离散余弦变换不同的是，小波变换编码不产生或消除[5]“块效应”和“蚊虫噪声”。另外，小波变换将图像分解为一些不同颜色、不同方向的子图像，这为利用人类视觉特性编码，进一步提高编码效率提供了条件。

1.2 小波变换在医学图像融合中的应用

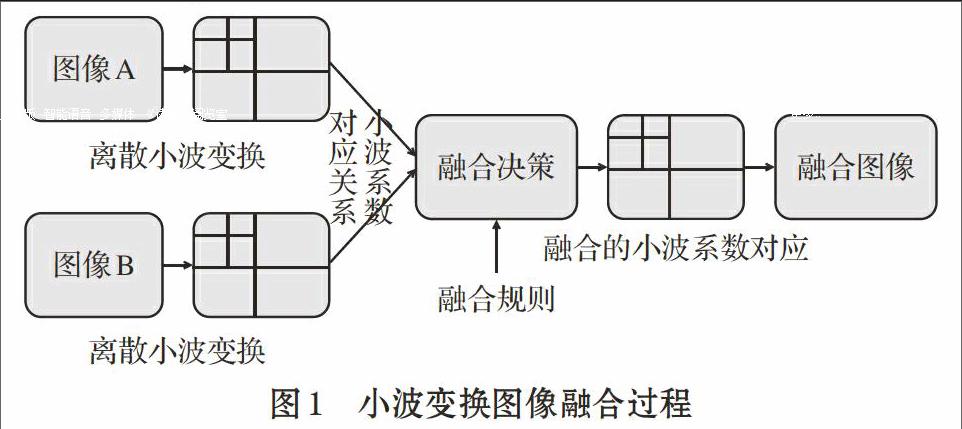
一个通用的基于小波的图像融合方法如图1所示。医学融合图像综合了不同成像模式的图像信息[6]，可提供比单一成像模式图像更好的显示效果和更丰富的诊断信息。

例如将正电子发射型计算机断层（PET）图像与X射线计算机断层图像（CT）进行融合（图2），在结果图像上既能表现精细的解剖结构又能反映某种代谢信息在其上的原位表达[7]，而这种综合信息则是无法从单一PET或CT图像上所能获得的，对于临床诊断具有非常重要的意义。

1.3 小波变换在生物医学图像去噪声中的应用

小波变换去噪声的基本原理是利用小波变换将含噪声图像分解到多尺度中，然后在每一尺度下把属于噪声的小波系数去除，保留并增强属于图像信号本身的小波系数，最后重构出利用小波变换去噪声后的图像。目前超声图像去燥的技术有：中值滤波、均值滤波、Frost滤波等，单一尺度滤波是上述几种方法常用的技术。小波变换具有低熵性、多分辨率性、去相关性、基函数灵活性等特点，在医学图像去燥上有无可比拟的应用优势[8]。

利用小波变换进行图像分解时，要想得到高信噪比的图像，就需对图像进行大尺度地分解处理，这样可以去除噪声，提高信号的集中度[9]。如高斯噪声，在平方最小的前提下降阀值T设置为：ln（N），其中，σ指的是噪声的方差，N指序列长度，利用阀值函数获取阀值T，再使用如下公式：

处理变换后的ω起到降低噪声信号的作用。

微阵列成像被认为是基因表达的大规模分析的重要工具。基因表达的准确性依赖于实验本身和进一步的图像处理。众所周知，实验期间引入的噪声将极大地影响基因表达的准确性，因此如何消除噪声的影响成为微阵列分析中的一个具有挑战性的问题。传统方法是当处理微阵列图像时使用统计学方法来估计噪声水平。一种涉及微阵列图像处理过程固有噪声的新方法，是在进一步图像处理前应用小波变换去除图像噪声，小波变换的时不变特性在对样品微阵列图像去噪声方面特别有帮助。

1.4 小波变换在医学图像边缘检测中的应用

边界探测在图像分割中扮演着重要角色。在许多情形下，对于图像分割和本身具备图像分割必要条件的边界探测方法而言，边界描绘是一个最终目标。换言之，许多分割技术需要目标边界的估计以实现其初始化。例如，用标准的基于梯度的可变形模型，应用边界图来确认必须停止的变形界面的位置。在这里，分割方法的最终结果强烈地依赖精确性和最初边界图的完整性。尽管有许多研究通过引入非边界约束来限制这种相互间的依赖性，但改善边界估计处理本身不仅是必需的而且是同等重要的。基于一阶或二阶导数的小波函数可用于多尺度边界探测。大多数多尺度边界探测方法，以多变的尺度平滑输入信号并且根据它们的一阶或二阶导数以探测剧烈变化的区域（边界）。

一阶导数小波函数更适合于边界探测。小波系数的大小代表了边界的相对“强度”，因此能够从噪声导致的微小的涨落中区别有意义的边界。总之，与已知的图像锐化算法相比，小波变换用于图像边界探测的一个明显优势是，可以获得不同尺度的边缘信息，换言之，即可以根据不同的要求得到不同精细程度的图像边界信息。

1.5 小波变换在医学图像增强中的应用

图像的轮廓主要体现在低频部分，而细节部分则体现在高频部分，因此，采用基于小波变换的图像增强技术可以通过对低频分解系数进行增强处理，对高频分解系数进行衰减处理达到图像增强的作用（图3）。

胃部超声扫描图像像素的灰度值常因集中于低灰度值一端而导致图像偏暗，而且超声图像受到大量斑点噪声的干扰，信噪比较低。调整显示器亮度，可在一定程度上获得改善，但亮度调整对于图像增强几乎没有作用。利用直方图均衡重新分配灰度值趋向于均匀分布，可提高整体亮度和对比度，但在直方图均衡化过程中由于将若干灰度值分布较少的像素合并于一新的灰度值中，从而在均衡后灰度值发生密度减少导致图像信息量的部分损失。因此，在直方图均衡化后再利用基于小波变换的增强算法，以增强信息量并同时强化图像。经小波变换处理后的图像信息熵显著增加，并能有效的强化胃窦轮廓，图像整体对比度有了明显改善（图4）。

2 小波变换在医学图像处理中的局限性

小波变换也有其固有缺陷，其空间局部性与其频谱的局部性不能很好地同时兼顾，通常只能择优选取。小波变换的计算、分解非常复杂，大量的数据运算需要耗费大量的运算时间， 特别在临床诊断中还有待进一步于改进。利用小波处理图像时，在保证图像处理的时间和质量的同时，对不同的图像根据图像自身的特点自适应地选择效果最佳的小波基是一项至关重要的研究工作，前文也提及小波基一词，它在小波变换中具有非常重要的作用。将小波作为一种基于被分析的函数或信号作内积来展开是不够的，还应考虑预处理和后续处理，考虑结合其他方法综合应用，使小波的应用更加广泛[10] 。

3 总结小波变换与展望

小波变换自产生起就成为数学的一个重要分支，在图像处理上得到了广泛应用。在医学图像处理上应用小波变换可以帮助医生提高临床确诊率。

与傅立叶变换相比，小波变换在时域和频域同时具有良好的局部化性质，能够在不同尺度上展开信号，更适合于处理突变信号和非平稳信号，在医学中的应用取得了良好的效果，如：用于医学图像压缩， 具有压缩比高、压缩速度快、压缩后能保持信号与图像的特征基本不变、边缘锐化较好等优点；用于X线图像中病变组织的边缘检测，其效果远优于最好的单尺度方法；CT、MR 医学图像采用小波分析方法融合处理后，可有效地保留原始多源图像的边缘和纹理特征，避免了融合图像因平均化出现模糊现象。将小波变换的图像分割、二维建模、三维变换、自适应量化等各项技术综合起来，并结合人类视觉特点，采用不同的压缩和增强方法，是远程医学图像传输发展的必然趋势[11] 。

另外，提及的小波基应用，它在小波变换中具有非常重要的作用，进行医学图像处理时，选择的小波基是否合理关系到图像处理效果，所以，小波基研究是小波变换发展的一个重要内容[12]。在医学图像处理中，还需二者有机结合利用，提高图像处理效果。

总之，小波分析技术的灵活性、快速性、双域性等特点决定了其在医学图像处理中的优势，与其他方法结合时更能发挥重要的作用。

参考文献（References）：

[1] 李弼程，罗建书.小波分析及其应用[M].电子工业出版社，2010.

[2] 刘惠，郭冬梅.医学影像和医学图像处理[M].电子工业出版社，2013.

[3] 李文书，赵悦.数字图像处理算法及应用[M].北京大学出版社，2012.

[4] 张玲.医学图像处理中的小波变换应用[J].中国医学影像技术，2010.26（2）：372-374

[5] 李玮琳.平移不变小波医学图像融合方法[J].长春工业大学学报（自然科学版），2013.34（6）：653-655

[6] Lee N，Choi Y.A modified OSEM algorithm for PETreconstruction using wavelet processing. Computerized Medical Imaging and Graphics，2005.80（3）：236-245

[7] Goetze S1， Wah1 RL. Prevalence of misregistration between SPECT.and CT for attenuation-corrected myocardial perfusion SPECT.J Nucl Cardiol，2007.14（2）：200-206

[8] 郭敏，马远良，朱霆.基于小波变换的医学超声图像去噪及增强方法[J].中国医学影像技术，2006.22（9）：1435-1437

[9] 李洪海，朱霞.采用双树小波变换的医学图像融合方法及实现[J].计算机应用与软件，2012.29（11）：292-294

[10] 杨军，彭承琳，吴宝明.小波分析在医学中的应用[J].国外医学（生物工程医学分册），2002.25（2）：89-92

[11] 乔灵宝.小波分析及其在医学中的应用[J].数理医药学杂志，2003.16（2）：155-156

[12] 苏小英.小波变换在医学图像去燥中的应用研究[J].数理医药学杂志，2011.24（2）：223-225