初中数学解题教学策略研究

周 东（浙江省武义县实验中学）

初中数学解题教学策略研究

周 东
（浙江省武义县实验中学）

解题教学在初中数学教学活动中之重要，所花精力之多，都是数学教育工作者所公认的。然而，在当前的解题教学中还存在很多问题，效果不尽如人意。如何提高解题教学的实效性，通过研究得出，解题教学要落实好数学基础知识；解题教学要教会学生解题思想方法；解题教学要形成解题思路，提高解题效率。从以上三个方面抓解题教学能达到事半功倍的效果，从而使解题教学达到高效，使学生学得轻松又有成效。

初中数学；解题教学；策略

当前，教师对解题教学也还存在认识的不足，停留在讲一题是一题，只为解决这个问题的水平。缺少题后反思，没有把问题教学提升形成思想方法和解题策略。学生一天做到晚做不完的练习，教师一天到晚改不完作业，讲不完的错题。因此，笔者就如何提高数学解题教学实效进行思考研究，谈一点粗浅的认识。

一、解题教学要注重落实数学基础知识

通过练习来巩固课堂上所学的数学知识，这是我们一直以来的做法，也收到了较好的效果。只有通过练习才能加强对数学知识的理解记忆。在解题教学中一定要加强落实该习题相关的数学知识，这是解题教学最根本的目的。

例1.已知：△ABC中，∠A=64°，角平分线BP、CP相交于点P。

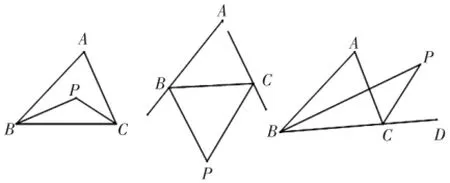
（2）若BP、CP是两外角的平分线，则∠BPC=_____（直接填数值）；

（3）若BP、CP是一内角的平分线，一外角的平分线，则∠BPC=（直接填数值）；

（4）由①②③的数值计算可知：∠BPC与∠A有着密切的数量关系，请就第②③写出你的发现。

分析：此题考查的数学知识是，三角形内角和定理；三角形的角平分线性质；三角形的外角性质。①根据三角形角平分线的性质可得，∠BPC+∠PCB=90°-∠A，根据三角形内角和定理可得∠BPC=90°+∠A；

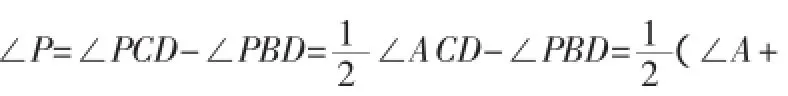
④根据前面的情况直接写出∠BPC与∠A的数量关系。

只有把数学知识分析透彻，让学生明白题目考查的基础知识，并对知识点加以梳理形成知识体系，才便于记忆。这是解题教学的首要任务，相当于摩天高楼的墙脚，只有掌握了基础知识，才能提炼数学思想方法。

二、解题教学要教会学生解题的思想方法

布鲁纳提出：“掌握数学思想和方法可以使数学更容易理解和更容易记忆，领会基本思想和方法是通向迁移大道的‘光明之路’”。因此，解题教学中要善于挖掘题目的内涵，总结提炼解题过程中蕴含的数学思想方法，积极引导学生用数学思想方法帮助找到解题思路。

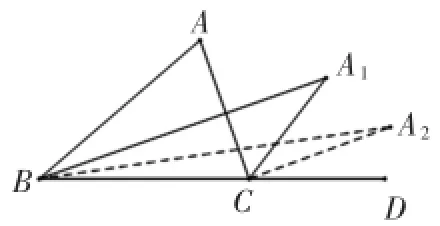
例2.如右图，在△ABC中，∠A= α.∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点 A2，得∠A2； …；∠A2011BC与∠A2011CD的平分线相交于点A2012，得∠A2012，则∠A2012=______.

这题考查的知识点和上一个例题是一样的，都是三角形内角和定理；三角形的角平分线性质；三角形的外角性质。我们可以用例1的整体带入的方法，转化的思想解决，达到举一反三的效果。在解题教学中要从以下几个方面去教会学生解题的思想方法。

1.在问题解决过程中，运用数学思想方法

在解题教学过程中要注重思想方法的分析，把数学课讲活、讲懂、讲深。数学中的化归、数学模型、数形结合、类比、归纳猜想等思想方法。数学思想方法在解题思路探索中的渗透，可以使学生的思维品质更具合理性、条理性和敏捷性。

2.在题后反思中，提炼数学思想和方法

解题后，教师应该为学生创造反思的机会，引导学生积极主动地提出问题，总结经验。如，解法是怎样想出来的？关键是哪一步？自己为什么没想出来？能找到更好的解题途径吗？这个方法能推广吗？通过解这个题，我学到了什么？在必要时可以引导学生进行讨论。

例3.例1的题后反思，“还有其他方法吗？”引导学生把图1叠放在图2和图3上，图2就可以利用四边形BPCP′的内角和360°求出，即∠P=360-∠PBP′-∠PCP′-∠P′。图3中∠P=∠BP′C-∠PCP′。这样通过对题目的反思，达到方法的创新。体验数学知识的内在联系，感受数学的简洁美。

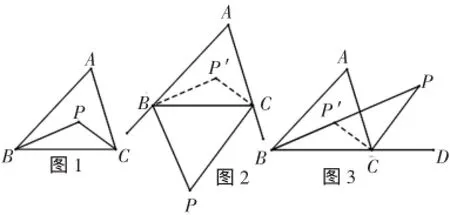
3.提倡一题多解、一题多变

让学生在一题多解、一题多变的过程中透过问题现象看清问题的本质，引导学生对变换后的题型进行比较、分析，加深对知识的理解和掌握，从而体会问题中所蕴含的数学思想和数学方法，找到问题的“根”，以不变应万变。

三、解题教学要形成解题思路，提高效率

解题后的回顾与探讨就是对解题的结果和解题的方法进行总结和提炼，对解题中的主要思想观点、关键因素及同类问题的解法进行概括、推广，从而帮助学生从中提炼出数学的基本思想和基本方法并加以掌握，提高解题效率。

例4.已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H。

图①

图②

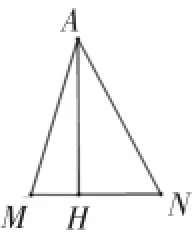
图③

（1）如图①，当∠MAN点A旋转到BM=DN时，请你直接写出AH与AB的数量关系____：__；

（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；

（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长。（可利用（2）得到的结论）

反思：（1）45°角能给我们什么启示？（2）可以将两条线段之和转化为同一条线段。问题（3）的解决可以借鉴问题（2）的图形和方法。通过这样的练习设计安排，让学生形成一定的解题定势，寻找（1）（2）小题与第（3）小题的联系，就能引导学生更深入的思考，训练思维。解题后提炼方法的推广，可以提高解题效率，把结果推广到一般的情形，从而研究结论。在原有条件、结论的基础上，进一步发展其空间形式或数量关系所得到的变化。解题后思想方法的推广，是培养学生积极思维、发明发现、创造突破能力的有效途径。如果能让学生养成习惯，那么就可以在解题训练中跳出“题海”，提高解题效率。通过少而精的解题，收到最大化的效益。

初中数学解题教学，只有通过上述的落实基础知识，掌握思想方法，形成解题思路等方面，有目的地去选题、编题、见解，才能达到事半功倍的效果，达到做一题、会一类、通一片的目标，使学生学得轻松，教师教得快乐。

［1］马复.初中数学教学策略［M］.北京师范大学出版社，2010-08.

［2］王卫标，鲍建立.初中数学提出问题教学研究［M］.北京师范大学出版社，2012-12.

·编辑 薄跃华