浅谈分类讨论思想在中学数学中的应用
2016-08-15何昌云甘肃省临夏回族自治州和政中学
何昌云(甘肃省临夏回族自治州和政中学)
浅谈分类讨论思想在中学数学中的应用
何昌云
(甘肃省临夏回族自治州和政中学)
分类讨论思想是解决问题的一种逻辑方法,也是一种数学思想,这种思想在简化研究对象、发展思维方面起着重要作用,因此,有关分类讨论的思想的数学命题在高考试题中占有重要地位.
分类讨论思想;中学数学;应用
所谓分类讨论,就是在研究和解决数学问题时,当问题所给对象不能进行统一研究,我们就需要根据数学对象的本质属性的相同点和不同点,将对象区分为不同种类,然后逐类进行研究和解决,最后综合各类结果得到整个问题的解决,这一思想方法,我们称之为“分类讨论的思想”.下面分析一下分类讨论思想在中学数学中的应用.
一、分类讨论思想在集合中的应用
解∵A={x-2≤x≤a},
∴B={y y=2x+3,x∈A}
={y-1≤y≤2a+3}.
与-2≤a≤0矛盾.
解得-1≤a≤3,
故2<a≤3.
二、分类讨论思想在函数中的应用
例2.已知函数f(x)=2x2-2ax+3在区间[-1,1]上有最小值,记作g(a),求g(a)的函数表达式.
在x=-1时,g(a)=2a+5;
(2)当-1<a<1时,即-2<a<2时,2
在x=1时,g(a)=5-2a;
三、分类讨论思想在不等式中的应用
例3.解关于x的不等式x2-(a+a2)x+a3>0.




四、分类讨论思想在排列组合中的应用
例4.在正方体的顶点中,12条棱的中点,6个面的中心及正方体的中心共27个点中,共线的三点组的个数是多少?
解:依题意,共线的三点组可以分为三类:
所以总共有28+3+18=49(个)。
五、分类讨论思想在数列中的应用
例5.已知数列1,2x,3x2,4x2,……,求它的前n项和.
分析:本题未指明数列为等比数列,所以分类讨论时还要考虑x=0这一情况.
解:设Sn=1+2x+3x2+…+nxn-1,
(1)当x=0时,Sn=1;

(3)当x≠0且x≠1时,
由Sn=1+2x+3x2+…+nxn-1,
得xSn=x+2x2+3x3+…+(n-1)xn-1+nxn,
两式相减:

综上所述:
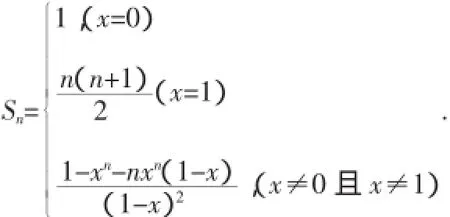
通过探讨分类讨论思想在中学数学中集合、函数、不等式,排列组合等中的应用,我们应用正确的分类讨论思想,对不同情况进行分类研究,使问题化整为零,各个击破,再积零为整,从而使复杂的问题得到清晰、完整、严密的解答.所以,在教学中教师应该渗透分类讨论的思想,让学生充分感受并掌握这种思想.
[1]郭可银.谈分类讨论思想方法在解题中的应用:高中版[M].高等教育出版社,2005-04.
[2]刘文武.中学数学中重要的数学思想:分类讨论思想[M].科学出版社,2003-11.
·编辑 薄跃华
