含分布式电源的配电网重构优化算法研究

李季，余健明

（商洛学院电子信息与电气工程学院，陕西商洛 726000）

含分布式电源的配电网重构优化算法研究

李季，余健明

（商洛学院电子信息与电气工程学院，陕西商洛 726000）

针对含分布式电源（Distributed Generators，DG）配电网络优化运行的问题，进行了配电网重构优化算法的研究，对含有DG的配电网络应用改进二进制粒子群优化算法进行重构，建立基于多种负荷方式（最大、最小、一般负荷方式）的配网重构模型，建立计及DG的配网辐射状判定依据，并对配电网潮流计算进行了改进，使其适用于拓扑结构变化频繁的网络。最后运用IEEE33节点测试系统对所提算法进行仿真验证，结果表明所提优化算法可使含DG配电网络的网络损耗明显降低，在一定程度提升系统的电压水平。

配电网络重构；二进制粒子群优化算法；分布式电源

近年来，分布式电源（DG）发展迅速，大量分布式电源不断接入电力系统，使得配电网结构发生了巨大变化：由单电源模式转变为多电源模式，分布式电源并网的容量、位置等会对配电网产生诸多影响，主要表现在配电网络的网络损耗、电能质量、系统稳定性、继电保护等方面，并使配电网结构及运行复杂化。因此，研究含DG配电网的重构具有重要的理论意义和实际价值［1］。目前对DG接入配电网后对配网重构产生影响的研究还比较少，含DG的配网重构可看作一个多目标组合优化的问题，与不含DG的配网重构相比，其具有更为复杂、规模更大、非线性等特点［2］。求解配电网重构的常用方法可分成启发式方法和人工智能算法两大类［3］。文献［4］在配网的重构数学模型中考虑了DG的影响，对含有DG的配电网络重构运用改进的遗传算法进行分析。文献［5］对含风电配电网运用粒子群引导最小树算法进行重构。文献［6］则在配网重构中采用了改进的二进制粒子群算法，并形成了辐射状判定依据。本文拟建立配电网络辐射状运行结构的判定依据，改进传统的配网潮流计算方法，提出基于环路编码的改进二进制粒子群算法，用于解决含DG的配网重构问题，并运用IEEE33节点测试系统进行验证分析。

1　配电网重构模型

本文考虑多种负荷方式下，以一年内系统综合有功网损最小为目标函数，数学模型如下：

上述目标函数的约束条件如下：

1）潮流约束条件

式中：Pi、Qi表示节点i处输入的有功、无功；PDG、QDG表示DG向节点i注入的有功、无功；PLi、QLi表示节点i所带负荷的有功、无功；Ui、Uj表示节点i，j的电压；N表示节点总数；Y表示支路的导纳矩阵。

2）节点电压约束条件

式中：Uimax、Uimin表示节点i的电压上下限值。

3）支路电流约束条件

式中：Ii、Ii max表示各支路电流及该支路所容许电流的最大值。

4）网络辐射状约束条件

网络重构后，配电网需呈辐射状结构。

2　二进制粒子群优化算法

文献［7］在研究鸟群觅食行为的基础上提出了基于群智能的演化技术，后又提出了离散二进制算法。

每个粒子的速度和位置更新公式为：

式中，i表示粒子编号；k表示迭代次数；v表示粒子的当前速度；d表示d维分量；x表示粒子的当前位置；pbest表示粒子的个体最优位置；gbest表示粒子种群最优位置；c1、c2为加速因子；r1、r2为介于两个均匀分布在（0，1）的随机数；ω为惯性权重。

二进制粒子群算法将粒子每一维限制为0和1，对应于开关的状态为开和合，粒子维数代表参与重构的开关数目。速度的大小则决定粒子位置取1的概率。考虑配电网络的重构特点，可对二进制粒子群算法做出改进。

2.1编码方式的改进

实际配电网中各类开关的数量较多，若直接对配网中各开关按照传统的二进制粒子群算法进行编码，则会生成庞大的粒子维数，对算法搜索效率产生严重影响。结合实际配电网的特点，为保证对用户供电的可靠性，需对配网结构做出下列限制：需闭合直接与电源或DG相连的开关；需闭合不在任一环路中的开关。以上开关对应的粒子位置始终为1，即以上开关不参与重构。

2.2粒子更新公式的改进

粒子群的适应值分布类似正态分布，假设粒子群进化到第I代，粒子适应值的平均值为μ，均方差为σ，速度更新公式调整为：

式中，ω表示粒子前次迭代速度对粒子当前速度的影响。

1）若Fi-μ＜-σ，则表示粒子的适应值很小，离目标函数很近，对于这种粒子应减慢其收敛速度，避免丧失粒子多样性，采用认知模型。

2）若-σ≤Fi-μ＜σ，则表示粒子的适应值适中，采用完全模型。

3）若Fi-μ＞σ，则表示粒子适应值很大，离目标很远，应加快其收敛速度，采用社会模型。

本文采用自适应动态惯性权重的调整策略，公式为：

2.3.2 学生评价。实习完成后，进行不记名问卷调查形式进行评价，条目包括[3]：a（是/否）提高临床思维逻辑推理能力；b（是/否）增加学习兴趣和学习热情；c（是/否）能够更加深刻的理解理论知识；d（是/否）提高分析和解决问题能力；e（是/否）提高语言表达能力；f（是/否）增强团队协作；g（是/否）提高自学能力；h（是/否）提高文献检索能力；i（是/否）有必要开展EBM+PBL教学。

式中：r为［0，1］区间内的随机数，函数Sigmoid定义为Sigmoid（x）=1/（1+e-x），K表示与开关d处于同一环网内的所有开关的集合。通过对粒子位置的更新的改进，可以确保网络为辐射状的结构，这样就避免了不必要的搜索，提高了算法的效率。

3　含DG的配电网重构

3.1含DG的辐射型网络的判定

DG的接入使配网结构复杂化，但依然呈现开环运行、闭环设计的特点，因此加入DG后，传统判定配网辐射状的方法仍然适用。由图论可知：有n个节点的辐射型网络，有且仅有一个根节点，该根节点与其余n-1个节点之间仅有一条通路。由此可得配网的辐射状判定依据：在所有节点均连通的条件下，闭合支路数等于网络中的节点个数减1。此判据成立的条件为：

1）闭合支路数=节点个数-1；

2）配网中不存在孤立节点或电力“孤岛”，即网络是连通的。

在含DG的配电网络中，对上述两个条件都要做出判断，形成辐射状判定的充要条件，提高算法的效率。

3.2含DG的配电网潮流计算

在配网的重构过程中，需进行反复多次的潮流计算，配网潮流计算构成了配网重构的基础。本文考虑了广泛应用的光伏及风电这两种类型的分布式能源，计算其接入配网的潮流。

1）DG的潮流计算模型

经由电流逆变器并网的光伏发电等DG可作为PI节点。其潮流计算模型为：

异步风机等DG通过吸收无功来建立磁场，一般可以认为是P恒定，V不定，Q由P和V来决定。即为PQ（V）节点，其潮流计算模型为：

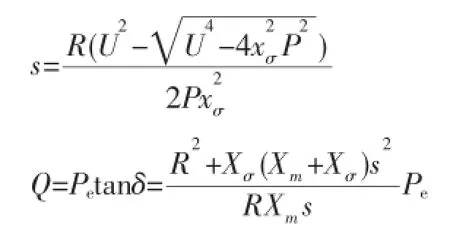
通过以上方法都可以将PI节点或PQ（V）节点处理为PQ类型的节点。即本文将DG做PQ节点处理。

2）含DG的配电网潮流计算

本文采用文献［9］中的改进前推回代方法，该方法适用于拓扑变化频繁的网络，因此适用于求解配网重构中的潮流问题。将DG等效成“负的负荷”后，该方法依然适用于加入DG后的配网潮流计算。

3.3算法总流程

1）读入原始数据：包括各种负荷方式下的各节点负荷、配网各支路参数、DG的安装位置及容量、粒子群规模、优化变量维数、最大迭代次数、以及加速因子等参数；

2）初始化：按照基于环路的编码方式，随机对一群粒子的位置及速度进行初始化；

3）检查粒子所对应的网络结构，若不满足辐射状要求，则重新对其进行初始化。

4）调用配网潮流计算模块，算出粒子适应值，粒子当前位置为其历史最优值，适应值最小的粒子位置为全局最优值。

5）更新粒子的位置及速度，若越界则取相应极值，并检查相应的辐射状约束条件是否满足，方法同步骤3。

6）计算粒子适应值。

7）判断迭代次数Imax是否达到最大值，若达到则终止程序，否则转到步骤5。

3.4基于多种负荷方式的配电网重构

实际配电系统中各节点负荷时刻都在变化，以网损最小为目标得到的最优网络结构不可能是固定不变的，但是由于目前配电网自动化程度低，开关频繁变换操作是不可行的。因此本文在某时间段（一年）内，用最大负荷，一般负荷，最小负荷来模拟负荷的变化。每种负荷方式下对应一种DG的运行方式。

假设一年当中最大负荷方式占2000 h，一般负荷方式占4760 h，最小负荷方式占2000 h，即Δt1=Δt3=0.23，Δt2=0.54。

求解多种负荷方式的含DG的配网重构的步骤如下：

1）在三种负荷方式下，按本文算法分别求解出三种最优重构结果。

3）计算每种方案的综合网损

找出最小的Fmin所对应的重构方案即为最佳方案。

4　算例分析

4.1算例

本文算例采用图1所示的IEEE33节点系统。

图1　IEEE33节点网络拓扑图

对其进行六种方案的重构：其中方案1-5为不考虑负荷变化的重构。方案6为考虑多种负荷方式的重构。

方案1：对不含DG的配网进行重构。

方案2：计及单个DG：18节点接入容量为80+j60 kVA的DG。

方案3：注入不同容量的DG：18节点接入容量为150+j90 kVA的DG。

方案4：在不同节点加入DG：25节点接入容量为80+j60 kVA的DG。

方案5：分别在18节点和25节点接入容量为100+j60 kVA和50+j30 kVA的DG。

方案6：考虑多种负荷方式的配网重构：其DG的运行方式如表1所示。

表1　DG安装节点及容量

4.2结果与分析

六种方案的重构结果如表2、表3所示。

表2　方案1-5的重构结果

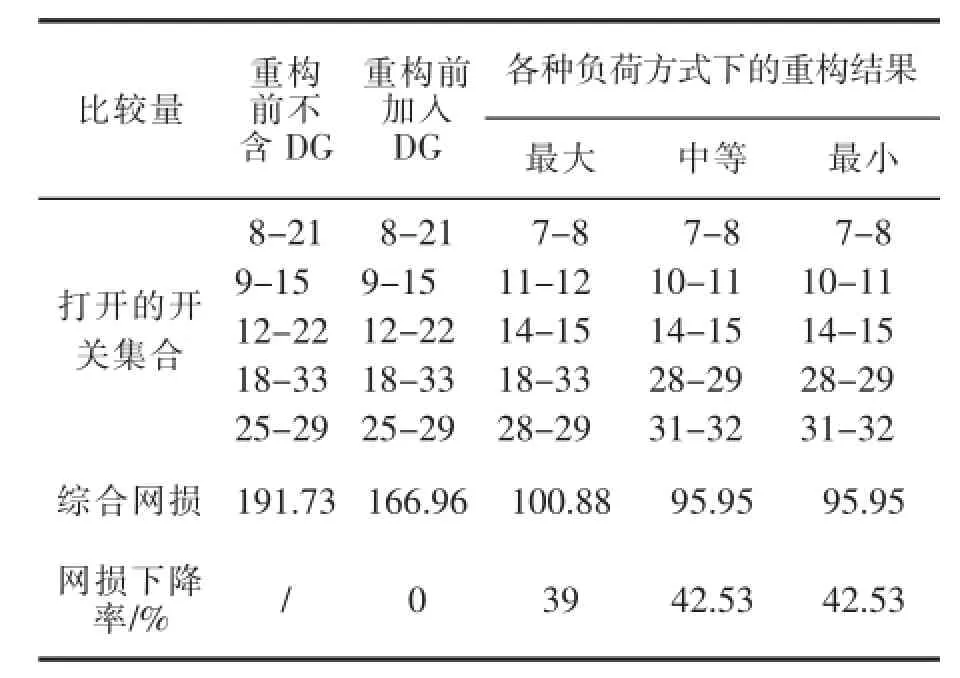
表3　方案6的重构结果

比较以上几种方案的结果，可得如下结论：

1）DG接入后，在开关设置合理时，可以明显降低配网的网损。

2）通过对表2及表3中方案2和方案6的结果比较可知：含DG的配网在进行重构时，其重构方案因DG的接入位置和容量的不同而不同。

3）比较表2中方案3和方案5可知：在接入DG的容量相同时，分散接入比集中接入时配网重构后的网损降低的更明显。

4）在考虑多种负荷方式时，得到两种重构方案，最后经过计算，求解得到综合网损最小的方案，即最小负荷和一般负荷方式下的方案为最终的最优方案。优化后的网络有功网损为95.95 kW，比重构前的有功网损166.96 kW降低了42.53%。与文献［10］未接入DG重构后的网损相比，未接入DG的重构后的综合网损为147.00 kW，加入DG重构后的综合网损减少到95.95 kW，可见DG的加入可以进一步减少配电网的网损。

5　结论

本文改进了含DG的配电网辐射状运行的判定方法，可以快速判断网络是否符合辐射状的要求；对含DG的配电网潮流计算也进行了相关改进，使其适用于拓扑变化频繁的配电网，不需要对网络进行分层和繁琐的节点编号；采用多种负荷方式（大负荷、中等负荷、小负荷）来模拟负荷变化，使网络运行结构在一段时间内保持最优，结果也更加符合实际情况；最后用算例验证了所提算法的有效性。含DG的配电网重构与DG的并网位置及容量有很大关系，所以DG的优化配置与配电网重构的综合优化的研究是一大方向。

［1］黄涛，王倩，谭又宁，等.计及分布式电源的配电网重构研究［J］.电力学报，2012，27（3）：199-202，206.

［2］陈垚.航空液压系统配电仿真分析［J］.商洛学院学报，2014，28（2）：13-16.

［3］刘畅，黄民翔.含多种分布式电源的配电网重构优化研究［J］.电力系统保护与控制，2013，41（6）：13-18.

［4］薛海龙.含分布式电源的配电网络重构［D］.天津：天津大学，2009：15-16.

［5］魏辉，曾令全.含分布式电源的配电网络重构［J］.华北电力大学学报，2012，39（2）：23-27.

［6］周洁洁.配电网重构及分布式电源优化配置研究［D］.杭州：浙江大学，2015：13-15.

［7］刘宏江，李林川，张长盛，等.基于多种负荷方式的含分布式电源的配电网重构［J］.电力系统保护与控制，2012，40（11）：117-121.

［8］张孝顺.含分布式电源的配电网络重构研究［D］.西安：西安理工大学，2014：20-22.

［9］李如琦，谢林峰，王宗耀，等.基于节点分层的配网潮流前推回代方法［J］.电力系统保护与控制，2010，38（14）：63-66，139.

［10］吕林.基于多粒子群分层分布式优化的配电网重构［J］.电力系统保护与控制，2009，37（19）：56-60，68.

（责任编辑：李堆淑）

Distribution Network Containing Distributed Generators Algorithm Reconfiguration

LI Ji，YU Jian-ming
（College of Electronic Information and Electrical Engineering，Shangluo University，Shangluo726000，Shaanxi）

As to the problem of the optimal operation of distribution network with distributed generators （DG），distribution network reconfiguration optimization algorithm is studied，an improved binary particle swarm optimization algorithm reconstructed the distribution network with DG is used，the distribution network reconfiguration model is established which based on a variety of load mode（large，small，medium load mode），established radiate judgment basis of distribution network with DG，the power flow calculation of distribution network is improved，making it applicable to the network which topology changes frequently. Finally，IEEE33 node test system is used to simulate the proposed algorithm，the results showed that the proposed optimization algorithm of distribution network including DG can significantly reduce losses，enhance the voltage level of the system certain extent.

distribution network reconfiguration；binary particle swarm optimization；distributed generators

TM744

A

1674-0033（2016）04-0009-04

10.13440/j.slxy.1674-0033.2016.04.004

2016-03-22

李季，女，陕西商南人，硕士，助教