非平稳信号分析的广义解析模态分解方法

郑近德,潘海洋,程军圣

(1.安徽工业大学机械工程学院,安徽马鞍山243032;2.湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙410082)



非平稳信号分析的广义解析模态分解方法

郑近德1,潘海洋1,程军圣2

(1.安徽工业大学机械工程学院,安徽马鞍山243032;2.湖南大学汽车车身先进设计制造国家重点实验室,湖南长沙410082)

现有的非平稳信号分析方法都有各自不同的缺陷,短时傅里叶变换的时频分辨率受不确定性原理的限制,希尔伯特黄变换存在端点效应和模态混叠,易导致模糊的时频分布;解析模态分解只适合分析频率恒定的多分量信号;针对包含多个时变模态、特别是频谱重叠的非平稳信号,本文提出了一种新的信号分析方法——广义解析模态分解(Generalized Analytical Mode Decomposition,GAMD).GAMD通过广义傅里叶变换将时变频率转换为频谱可分的,采用解析模态分解对其分解,再对得到的单分量信号进行逆广义傅里叶变换即可得到原始信号的分量.因此,GAMD非常适合分析时变的非平稳信号.通过仿真信号将GAMD与短时傅里叶变换和希尔伯特黄变换等方法进行了对比,结果表明GAMD方法的分解效果更精确,时频分辨率更高.

时频分析;广义傅里叶变换;解析模态分解;经验模态分解;非平稳信号

1　引言

自然界中大部分信号是时变的、非线性(即由非线性系统产生)和非平稳的,适合处理线性和平稳信号的方法如傅里叶分析,不可避免地有一定的局限.时频分析方法因其能够同时提供信号时频域局部信息而在非线性信号分析方面得到了广泛的应用[1].常用的时频分析方法,如短时傅里叶变换,Wigner-Ville分布,小波变换和希尔伯特-黄变换(Hilbert-Huang Transform,HHT)等都有各自不同的局限,短时傅里叶变换是一种加窗口的傅里叶变换,时频分辨率受窗口大小的影响和不确定原理的限制[2];Wigner-Ville分布存在交叉项的干扰[3];小波变换具有严格的数学基础、分析精度高、具有高分辨率和多尺度分析的特征,已被相关学者应用到不同的领域[4,5],但是,小波分析需要事先确定小波基和分解层数,而且分解缺乏自适应性[6].希尔伯特-黄变换是美籍华人HUANG E院士等提出的一种自适应的非平稳信号分析方法[7～9],包括经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特变换两部分,EMD是一种基于数据本身、完全数据驱动的信号分解方法,不需要事先选择基函数,能够自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的内禀模态函数(Intrinsic Mode Function,IMF)之和,再通过对每个IMF分量进行希尔伯特变换得到瞬时幅值和瞬时频率,进而可得到原始信号完整的时频分布.EMD方法自提出后在图像处理,语音信号处理和机械故障诊断等多个领域都得到了广泛应用[10～12].但是,EMD方法的可分辨的频率范围有限,特别是对于包含密集模态的多分量信号,EMD会出现模态混叠现象.

解析模态分解(Analytical Mode Decomposition,AMD)[13]是WANG和CHEN最新提出的一种时频分析方法,能够有效地分离频率非常密集的非平稳信号,并且成功识别自由振动下具有密集模态的三自由度系统.但是,AMD只适合分析各模态频率为常函数、且频谱无重叠的多分量信号,而对于实际的非平稳信号,通常包含多个模态,它们的瞬时频率是时变的,且在频域内有交叉重叠,此时AMD无法分解出.

为了克服AMD的缺陷,本文提出一种适合分析包含时变模态的非平稳信号的方法——广义解析模态分解(Generalized Analytical Mode Decomposition,GAMD).GAMD首先通过广义傅里叶变换将信号的时频分布是倾斜、非线性或曲线的变换为线性或近似平行于时间轴,在频谱无重叠可分的;其次,采用AMD对变换后的信号进行分解;再次,对得到的单分量信号进行逆广义傅里叶变换得到原始信号的真实单分量信号;最后,采用希尔伯特变换计算每个单分量信号的瞬时频率和瞬时幅值,进而得到原始信号完整的时频分布.通过仿真信号分析,将GAMD方法与短时傅里叶变换,广义解调和HHT等方法进行了对比,结果验证了GAMD的有效性和优越性.

2　解析模态分解

AMD的原理和计算方法简述如下[13,14]:

0≤ω1(t)<ωb1(t)<ω2(t)<ωb2(t)<…<ωi(t)<ωbi(t)<ωi+1(t)<…<ωn-1(t)<ωbn-1(t)<ωn(t)

其中,ωbi(t)为边界分割频率.由此,原始信号x(t)的每一个单分量信号可以由式(1)～(4)解析的给出:

s1(t)=sin(ωb1t)H[x(t)cos(ωb1t)]

-cos(ωb1t)H[x(t)sin(ωb1t)]

(1)

r1(t)=x(t)-s1(t)

(2)

si(t)=sin(ωbit)H[ri-1(t)cos(ωbit)]

-cos(ωbit)H[ri-1(t)sin(ωbit)]

(3)

ri(t)=ri-1(t)-si(t),(i=2,3,…,n)

(4)

其中,H[·]表示希尔伯特变换.AMD方法实际上是一个自适应的低通滤波器,其本质是利用希尔伯特变换将某一具有特定频率成分的信号解析的分解出.对于多个密集频率信号叠加的复杂信号,AMD通过构造一对具有相同特定时变频率的正交函数,并利用这对时变正交函数与原信号乘积的希尔伯特变换,把任意在频率时间平面内低于正交函数时变频率的信号解析的分解出来.另外,AMD方法即可以通过一次性选择所有边界截止频率,从而一次性得到所有的单分量信号,也可以一次只分解出一个单分量信号,从而经过多次选择二分类的边界截止频率,每次分解出相对低频的单分量信号;由于大部分多分量信号的所包含的模态在频谱并不是全部可分的,即有些相邻的模态可能会出现交叉或或重叠,而导致AMD方法无法辨识和分解.基于此,本文所采用的AMD方法中,每次只分解出一个相对低频的单分量信号和一个相对高频的剩余信号.这里一个关键的问题是低频和高频的边界截止频率的选择.文献[13]中选择分割频率为频谱中相邻的两个峰值的平均值.但这种方法只合适于所有模态都具有相同带宽的信号,而对于大部分多分量信号,每个模态的带宽未必相同,因此,仅仅依据峰值容易得到不合理的分解结果.论文对此进行了改进,提出了采用频谱中瞬时幅值的极大值和极小值共同决定分割频率的方法.具体步骤如下:(1)假设信号中无直流分量或趋势项,否则,假设原始信号的频谱在起始点即为极大值;(2)如果第一个峰值和第二个峰值之间只有一个极小值,则选此极小值为边界截止频率;如果第一个峰值之后无峰值,则选择其后的极小值为边界截止频率;(3)如果第一个峰值和第二个峰值之间还包含有多个极大值和极小值,且极大值和极小值远远小于第一和第二个峰值,则令两个峰值的平均值为边界频率.

3　广义解析模态分解

解析模态分解(AMD)能够分解频率接近的多分量信号,但是,AMD假设各个模态的频率是恒定的,即各个模态的频率在频谱无重叠.而对于包含时变线性或非线性频率的多分量信号,所含模态的频谱未必是可分的,此时AMD无法分解,EMD也会出现模态混叠,分解结果得到的分量失去了物理意义.为了解决上述问题,论文提出了广义解析模态分解方法(GAMD).

3.1广义傅里叶变换

一般地,多分量信号所包含的各个模态的瞬时频率并非互相平行的直线或者曲线,各个模态的瞬时频率未必有线性或非线性的关系,因此,无法只通过一次广义解调就能将各个分量全部都变换成频率恒定的信号.由于AMD方法的自适应低通滤波特性,每次可以只分离出低频的单分量信号,因此,只要使得广义傅里叶变换之后相邻模态的频率在频域可分、无重叠即可[15,16].

对于信号x(t),其广义傅里叶变换定义为[15,16]

(5)

式(5)中,s0(t)是时间t的实值函数,式(5)实际上是对x(t)e-j2πs0(t)做标准傅里叶变换,同样可以对XG(f)进行逆傅里叶变换得到x(t),即

(6)

3.2广义解析模态分解方法

一般地,对于任意一个多分量信号,它所包含的各个时变模态的时频分布是未必是线性的或平行的非线性曲线,更大可能是没有任何关系的.对于这种信号,只采用一次广义傅里叶变换无法将所有模态都变换为线性的.因此,广义解调时频分析方法不能处理这类信号;由于其模态是时变的,解析模态分解方法也无法处理这类信号.针对两种方法处理时变多分量信号的不足,本文提出了广义解析模态分解方法(GAMD).

假设多分量信号x(t) (t∈[t0,T]),GAMD方法的具体步骤如下:

(1)令r0(t)=x(t),k=1;

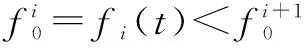
(a)频谱不可分,即:存在t1,t2∈[t0,T],s.t.fi(t1)>fi+1(t2);

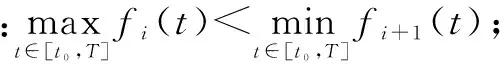
(4)令k=k+1;重复步骤(3),直到k=n,得到所有的分量xk(t),k=1,2,…,n;

(5)对每一个单分量信号进行希尔伯特变换,计算各个单分量信号的瞬时幅值和瞬时频率,得到每个分量的时频分布,进而得到原始信号的完整时频分布.

GAMD方法包含了三个步骤:(1)依据短时傅里叶变换估计模态个数和时变模态的相位函数;(2)对频谱不可分的模态进行广义傅里叶变换;(3)执行AMD和逆广义傅里叶变换.与短时里叶变换相比,GAMD方法明显地提高了时频分辨率;与原广义解调时频分析相比,GAMD通过迭代的方式每次只提取一个单分量信号,可以处理时频谱可分的模态、而不仅仅是瞬时频率是平行的直线或曲线的情况,因此,提高了广义解调时频分析的可分析信号的范围;与AMD相比,由于AMD方法只能处理时频谱可分且频谱可分的多分量信号,而GAMD不仅能处理这些,而且还可以处理时频谱可分但频谱有重叠的情况,大大提高了AMD的信号分析范围.因此,与现有方法相比,GAMD时频分辨率更高,分解能力更强.

事实上,本文提供了一种新的时频分析方法,即:首先,采用广义解析模态分解方法对信号进行分解,得到若干个单分量信号;其次,采用希尔伯特变换对单分量信号进行解调,得到它们的瞬时幅值和瞬时频率,进而得到原始信号的完整时频分布.

4　仿真信号分析

为了说明GAMD方法的有效性,首先考虑式(7)所示的仿真信号z(t)

z(t)=z1(t)+z2(t)+z3(t),t∈[0,1].

(7)

其中,z1(t)=e-tcos(2π·30t),z2(t)=(2t+1)sin(2πt(40+20t)),z3(t)=cos(2πt(60+20t)).信号z(t)由调幅信号、调幅调频信号和调频信号组成,其频谱如图1(a)所示,由于z2(t)和z3(t)的带宽较宽,而且二者的中心频率非常接近,因此,二者的频谱发生重叠,采用AMD方法无法对其进行分解.由于三者的瞬时频率非常接近,EMD方法分解的效果也不理想.

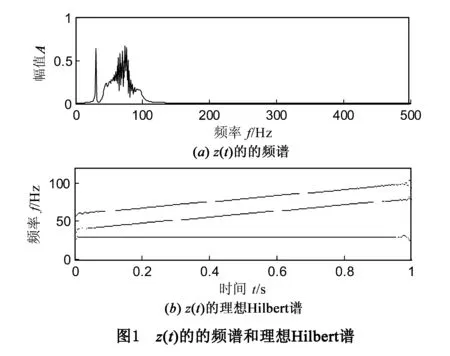
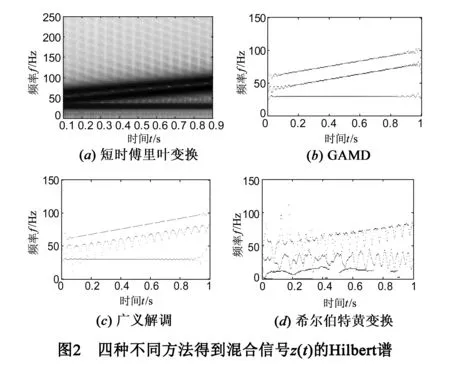
信号z(t)理想的Hilbert谱如图1(b)所示(为了便于对比,下文解调方法均为希尔伯特变换).在采用GAMD方法对其进行分析之前,先由短时傅里叶变换得到其时频谱,如图2(a)所示.由图可以看出,短时傅里叶变换得到的时频谱时频分辨率较低,但从中可以看出,混合信号包含了三个单分量信号,因此,由短时傅里叶变换的时频分布可以初步读取如下信息:混合信号包含三个模态;其中第一个低频模态和高频模态在频谱是可分的,由此估计对应的相位函数,采用GAMD方法对其进行分解,得到的各个分量如图3所示,图中实线为GAMD分解结果,虚线为对应的理想结果.由图中可以看出,除了Hilbert变换引起的轻微的端点效应外,GAMD方法得到的分量与对应的理想结果非常吻合,计算发现,它们与对应理想结果z1(t),z2(t)和z3(t)的相关系数分别为:0.992,0.998,0.996.GAMD分解分量的Hilbert谱如图2(b)所示,对比图2(b)和图1(b)也可以看出,GAMD结果与理想结果非常接近.

为了对比,再采用原广义解调时频分析方法[15]和希尔伯特-黄变换两种方法估计信号z(t)的Hilbert谱,结果分别如图2(c)和图2(d)所示.与理想结果相比,广义解调时频分析的Hilbert谱只有最高频和最低频的单分量信号的分解效果较好,而另一个单分量信号的估计结果与理想结果相比误差较大.希尔伯特黄变换得到的Hilbert谱发生了严重的模态混叠,各个模态无法区分.综上,此例初步表明了GAMD方法的有效性和优越性.

上例中,仿真信号包含了频率非常接近且为时变的单分量信号,GAMD能够有效地将各个单分量信号分离,而且得到的时频分布要比现有的短时傅里叶变换,广义解调时频分析和希尔伯特黄变换等方法得到的结果更精确.

不失一般性,再考虑式(8)所示的仿真信号y(t):

y(t)=y1(t)+y2(t)+y3(t)+y4(t)+y5(t)

(8)

其中,y1(t)=cos(2πt(30+20t+sin(2π·2t))),

y2(t)=cos(2πt(60+20t+30t2)),

y3(t)=cos(2πt(90+30t+30t2)),

y4(t)=cos(2πt(120+80t)),t∈[0,1].

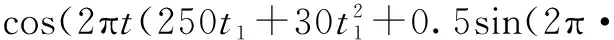
10t1))),t1∈[0,0.4].

y(t)由四个调频信号和一个高频间歇调频信号组成,其中,y1(t)是调频部分有线性而和正弦,y2(t),y3(t)和y4(t)调频的线性和多项式函数部分不互相平行,y5(t)是调频部分为线性和正弦频率的高频间歇信号.y(t)的频谱如图4所示,由于各单分量成分的中心频率非常接近,而且它们频谱重叠,AMD和EMD方法都无法分解.

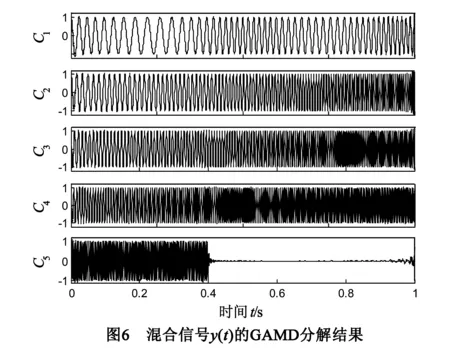
首先采用短时傅里叶变换得到其Hilbert谱,如图5(a)所示.短时傅里叶变换得到的时频谱时频分辨率较低,但从中可以看出,混合信号包含了五个单分量信号,因此,由短时傅里叶变换的时频分布得到每个单分量信号的近似瞬时频率,进而估计对应的相位函数.再采用GAMD方法对其进行分解,分解结果如图6所示,图中实线为GAMD分解结果,虚线为对应的yi(t)(i=1,2,…,5).由图5可以看出,除了分解得到的各个单分量信号Ci有轻微的端点效应,与yi(t)(i=1,2,…,5)吻合度较高,对应分量之间的相关系数分别为:0.999,0.999,1,1和0.996.由GAMD分解结果得到信号y(t)的Hilbert谱如图5(b)所示,y(t)理想的Hilbert谱如图5(c)所示,对比图5(b)和图5(c)可以看出,GAMD方法的结果与理想结果非常接近.同时,采用希尔伯特黄变换方法估计y(t)的Hilbert谱,结果如图5(d)所示,由图可以看出,由希尔伯特黄变换得到的Hilbert谱则发生了严重的模态混叠,各个模态无法区分.因此,上述两个仿真信号的分析结果表明了GAMD方法的有效性和相较于现有方法的优越性.

5　若干问题

5.1相位函数对分解结果的影响

相位函数的估计是广义傅里叶变换的关键,解调后信号的频谱可分与否则是解析模态分解的关键,因此,相位函数的估计是整个GAMD方法的关键.但是,相位函数的估计的精确性对分解结果影响不大,也就是说,GAMD并不需要十分精确地估计每一个模态的瞬时频率的相位函数而使得每一个模态的瞬时频率都变成恒定频率,而只需要估计的相位函数使得相邻的模态在频谱可分即可,而不需要使得相邻的两个模态都变成恒定的频率.广义解调的初衷是估计每一个模态的瞬时频率,进而估计对应的相位函数,使得解调后的模态是恒定的频率,如果混合信号包含k个时变的模态,则需要估计k个相位函数,使得每一次迭代中的模态都是恒定频率的.事实上,我们不需要这么做,我们的目的是通过广义解调变换,使得变换后的信号的模态在频谱是可分的,也就是说,如果混合信号包含k个时变的模态,那么我们只需要估计至多估计k-1个相位函数,而使得每一次迭代的低频模态与高频模态在频谱是可分的即可.

以式(8)所示的仿真信号y(t)来说明.为了分解模态y1(t)和y2(t),我们可以依据短时傅里叶变换预估计的时频分布中分别估计二者的近似瞬时频率,进而估计对应的相位函数,从而使得变换后二者的瞬时频率恒定,在频谱有明显的谱线,实现AMD分解.由短时傅里叶变换得到的时频谱预估计第一个模态的瞬时频率f1(t)=30+40t+2πcos(2π·2t),以及预估计的三个分割第一个和第二个模态的边界频率:f2(t)=45+60t,f3(t)=45+50t和f3(t)=50+36t,如图7(a)所示.由此四种瞬时频率分别估计四个不同的相位函数,再由此得到第一个模态的瞬时频率,如图7(b)所示,由图可以看出,四种不同的瞬时频率估计的相位函数所得到的第一个模态的瞬时频率非常接近,与真实值相差较小,这说明相位函数的估计精度对GAMD分解结果影响较小.

5.2噪声和采样频率对分解结果的影响

为了研究噪声和采样频率对GAMD方法分解结果的影响,仍以式(8)所示的混合信号y(t)为例,向y(t)中分别加入SNR为10dB和20dB的噪声,采样频率fs分别为2000Hz和8000Hz,分别采用GAMD方法对四种情况下的加噪信号进行分解,得到第一个模态的瞬时频率如图8所示.从中可以看出,噪声对GAMD方法的分解结果有一定的影响,噪声越大,对分解结果的影响也越大.但是,提高采样频率可以有效的提高GAMD的分解效果.

6　结论

提出了一种新的非平稳信号处理的时频分析方法:广义解析模态分解(GAMD).主要得到如下结论:

(1)GAMD方法通过广义傅里叶变换将时变的、频谱不可分的模态变换为频谱可分,采用AMD分解后再通过逆广义傅里叶变换即可得到原始信号的模态,因此,GAMD本质上是一种时变的解析模态分解方法.

(2)GAMD方法能够分解包含频率比较密集的信号,而且能够分解高频间歇信号,而不会引起模态混叠,通过将其与短时傅里叶变换、广义解调时频分析和希尔伯特黄变换方法进行对比,结果表明了GAMD的优越之处.

(3)研究了相位函数估计、噪声和采样频率等对GAMD分解结果的影响,结果表明,GAMD对相位函数的估计精度并不敏感;当混合信号中包含噪声时,通过提高采样频率可以有效的提高GAMD的分解效果.

尽管如此,广义解析模态分解也有不足,如自适应性不如EMD,依赖短时傅里叶变换等时频分析方法对信号模态的预估计等,这些问题笔者正在进一步研究中.

[1]冯志鹏,朱萍玉,褚福磊.基于自适应多尺度线性调频小波分解的水轮机非平稳振动信号分析[J].中国电机工程学报,2008,28(8):105-110.

FENG Zhi-peng,ZHU Ping-yu,CHU Fu-lei.Time-frequency analysis of hydroturbine nonstationary vibration signal based on adaptive multi-scale chirplet decomposition[J].Proceedings of the Chinese Society for Electrical Engineering,2008,28(8):105-110.(in Chinese)

[2]李允公,姚兆,刘杰,等.基于瞬时频率的窗宽递增寻优的短时傅里叶变换[J].东北大学学报:自然科学版,2007,28(12):1737-1740.

LI Yun-gong,YAO Zhao,LIU Jie,et al.Anovel STFT of window duration increasing optimization based on instantaneous frequency[J].Journal of Northeastern University(Natural Science),2007,28(12):1737-1740.(in Chinese)

[3]刘文艺,汤宝平,陈仁祥,等.一种应用自项抑制魏格纳分布交叉项的方法[J].中国机械工程,2009,20(21):2613-2616.

LIU Wen-yi,TANG Bao-ping,CHEN Ren-xiang,et al.A method to suppress the cross terms in Wigner-Ville distribution using auto terms[J].China Mechanical Engineering,2009,20(21):2613-2616.(in Chinese)

[4]徐小军,王友仁.基于离散分数阶正交小波变换图像降噪新方法[J].电子学报,2014,42(2):280-287.

XU Xiao-jun,WANG You-ren.Novel image denoising method based on discrete fractional orthogonal wavelet transform[J].Acta Electronica Sinica，2014,42(2):280-287.(in Chinese)

[5]王登,苗夺谦,王睿智.一种新的基于小波包分解的EEG特征抽取与识别方法研究[J].电子学报,2013,41(1):193-198.

WANG Deng,MIAO Duo-qian,WANG Rui-zhi.A new method of EEG classification with feature extraction based on wavelet packet decomposition[J].Acta Electronica Sinica，2013,41(1):193-198.(in Chinese)

[6]程军圣.基于Hilbert-Huang变换的旋转机械故障诊断方法研究[D].长沙:湖南大学,2005.

[7]HUANGN E,WU M L C,LONG S R,et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J].Proceedings of the Royal Society of London,A,2003,459 (2037):2317-2345.

[8]HUANGN E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London,A,1998,454 (1971):903-995.

[9]HUANGN E,SHEN Z,LONG S R.A new view of nonlinear water waves:the Hilbert spectrum[J].Annual Review of Fluid Mechanics,1999,31 (1):417-457.

[10]葛光涛,虞露.二维经验模态可分离度及其量化计算[J].电子学报,2013,41(7):1313-1318.

GE Guang-tao,YU Lu.The bidimensional empirical mode detachable degree and its quantum calculation[J].Acta Electronica Sinica,2013,41(7):1313-1318.(in Chinese)

[11]KALEEM M,GHORAANI B,GUERGACHI A,et al.Pathological speech signal analysis and classification using empirical mode decomposition[J].Med Biol Eng Comput,2013,51(7):811-821.

[12]LEI Y G,LIN J,HE Z J,et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing,2013,35(1-2):108-126.

[13]CHEN G D,WANG Z C.A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J].Mechanical Systems and Signal Processing,2012,28(2):258-279.

[14]WANG Z C,CHEN G D.Analytical mode decomposition

of time series with decaying amplitudes and overlapping instantaneous frequencies[J].Smart Materials and Structures,2013,22(9):95003-95016.

[15]OLHEDE S,WALDEN A T.A generalized demodulation approach to time-frequency projections for multicomponent signals[J].Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences,2005,461(2005):2159-2179.

[16]CHENG J S,YANG Y,YU D J.The envelope order spectrum based on generalized demodulation time-frequency analysis and its application to gear fault diagnosis[J].Mechanical Systems and Signal Processing,2010,24(2):508-521.

郑近德(通信作者)男,1986年生于安徽阜阳,博士,现为安徽工业大学机械工程学院讲师.研究方向为动态信号处理,时频分析及机械设备故障诊断,已发表学术论文30余篇.

E-mail:lqdlzheng@126.com;jdzheng@ahut.edu.cn

潘海洋男,1989年生于安徽宿州,硕士,现为安徽工业大学机械工程学院助教.研究方向为模式识别与机械设备故障诊断.

E-mail:pansea@sina.cn

程军圣男,1968年生于湖南永州,博士,现为湖南大学教授,博士生导师.主要从事机械故障诊断、动态信号分析与处理等方面的研究.

E-mail:signalp@tom.com;chengjunsheng@hnu.edu.cn

Generalized Analytical Mode Decomposition for Non-Stationary Signal Analysis

ZHENG Jin-de1,PAN Hai-yang1,CHENG Jun-sheng2

(1.SchoolofMechanicalEngineering,AnhuiUniversityofTechnology,Maanshan,Anhui243032,China;2.StateKeyLaboratoryofAdvancedDesignandManufacturingforVehicleBody,HunanUniversity,Changsha,Hunan410082,China)

The existing methods for analyzing non-stationary signal all have different defects.The time-frequency resolution of short-time Fourier transform is limited by the uncertainty principle.The boundary effect and mode mixing of Hilbert-Huang transform often result in an unclear time-frequency distribution.Analytical mode decomposition is only suitable for analyzing multi-component signal with constant frequencies.For the multi-component signal with time-varying frequencies,especially when the spectrum overlaps,a method termed generalized analytical mode decomposition (GAMD) is proposed for analyzing these signals.In GAMD,generalized Fourier transform is used to convert the time-varying frequencies to constant ones without overlapping in spectrum and then the analytical mode decomposition is adopted to handle the transformed signal.Lastly,the inverse generalized Fourier transform is used to demodulate the obtained mono-components.Hence,GAMD is very suitable for analyzing time-varying non-stationary signals.The proposed GAMD method is compared with short-time Fourier transform and Hilbert-Huang transform through analyzing simulation signals and the results indicate that GAMD possesses more accurate decomposing results and higher time-frequency resolution.

time-frequency analysis;generalized Fourier transform;analytical mode decomposition;empirical mode decomposition;non-stationary signal

2015-04-14;修回日期:2015-06-20;责任编辑:覃怀银

国家自然科学基金(No.51375152，No.51505002)；安徽省高校自然科学基金项目(No.KJ2015A080)

TN911.7

A

0372-2112 (2016)06-1458-07