认知MIMO干扰网络最优干扰对齐算法

朱世磊,郑娜娥,巴　斌,胡捍英

(解放军信息工程大学导航与空天目标工程学院,河南郑州450002)



认知MIMO干扰网络最优干扰对齐算法

朱世磊,郑娜娥,巴斌,胡捍英

(解放军信息工程大学导航与空天目标工程学院,河南郑州450002)

认知无线电通过与MIMO(Multi-Input Multi-Output)、OFDM(Orthogonal Frequency Division Multiplexing)、超宽带、协作通信等技术融合来改善频谱利用率.而认知MIMO是认知无线电和MIMO技术的融合,虽然具有干扰抑制、抗多径衰落、空间分集和复用等优势,但是由于underlay共享方式中干扰温度约束的存在,导致发送预编码矩阵之间相互耦合,因此该技术在underlay干扰网络中难以获得最优的传输性能.针对该问题,通过交替迭代的方式,结合Rayleigh-Ritz定理和凸优化理论,推导了最优收发矩阵之间的迭代关系,提出一种最优干扰对齐算法.该算法利用Lagrange部分对偶方式来去除干扰温度约束,并采用次梯度投影法更新Lagrange变量,克服了已有半正定松弛算法因忽略矩阵秩约束而导致速率性能下降的缺陷.理论分析和数值仿真验证了算法的有效性,结果表明所提算法可实现网络可达速率和的最大化.

认知MIMO;underlay频谱共享;干扰网络;干扰对齐;Lagrange部分对偶

1　引言

随着无线通信系统的发展,频谱资源稀缺与频谱资源利用率低之间的矛盾越来越受到人们的关注.认知无线电[1]通过高效灵活的频谱接入机制,在不影响主用户(Primary Users,PU)正常通信的前提下,可以与主用户网络共享频谱.频谱共享主要可分为交叉式(overlay)频谱共享和重叠式(underlay)频谱共享两种[2],其中overlay方式是指次用户(Secondary Users,SU)利用空闲的时间、频率或空间空洞完成通信,即“见缝插针”地使用PU未占用的通信资源实现机会式接入;而underlay方式允许主次用户使用同一资源,通过将次用户网络对PU接收端的叠加干扰限定在一定的干扰温度之下,保证PU的正常通信需求,从而避免了SU频繁的信道间切换.underlay方式以其较高的频谱效率和可实现性成为了一种具有吸引力的共享方式,被美国联邦通信委员会作为认知无线电系统的主要频谱共享方式[3].

随着认知研究的深入,关于SU与PU共存的研究已从最初的时域和频域拓展到空间域[4].与多输入多输出(Multi-Input Multi-Output,MIMO)的结合,利用其空域抗干扰和并行传输优势设计频谱共享方法,已成为当前认知的研究热点之一[4～7].干扰对齐(Interference Alignment,IA)技术作为MIMO抑制干扰的一种有效的技术手段,通过调整发送预编码矩阵将多用户干扰信号对齐压缩到低维子空间上,以实现频谱的高效共享.文献[5]的研究表明与传统频分复用的认知系统相比,IA技术可以显著提高认知系统的和速率.

近年来,MIMO干扰网络IA技术的研究已相对成熟,其中文献[6]提出的一种分布式IA算法最具代表性,其利用收发双发信道的互易性,通过交替迭代最小化目标函数的方式来获得最优的预编码矩阵,可实现网络速率和最大化.然而传统MIMO的IA算法由于缺乏对主用户接收端叠加干扰的控制,无法直接适用于认知MIMO干扰网络,目前对于认知MIMO干扰网络的IA研究较少,尚处起步阶段.文献[7]提出一种迭代的认知干扰对齐(Iterative Cognitive Interference Alignment,ICIA)算法.该算法通过正交投影的方式,先将SU的发射信号正交投影到PU未占用的机会空间上,来完全避免SU对PU的干扰;然后在机会空间上采用分布式IA算法[6]实现次用户网络内部的干扰对齐.但正交投影只能机会式地利用PU未占用空间,且正交过程会损失部分功率,导致可达的速率和受限.文献[8]针对underlay共享方式,允许SU使用全部的空间,并通过设置干扰温度门限来控制SU对PU的干扰.文中将认知MIMO干扰对齐问题建模为多约束的二次约束二次规划(Quadratically Constrained Quadratic Programs,QCQP),采用半正定松弛(SemiDefinite Relaxation,SDR)方法松弛PU干扰温度约束,来求解收发编解码矩阵.然而,SDR方法的求解过程中忽略矩阵秩的约束,所求得结果仅是最优预编码矩阵的一个估计,尤其在多子流传输时可能出现一定的估计误差,无法保证次用户网络的速率和最大化[8,9].

针对已有文献的不足,本文主要采用Lagrange部分对偶,将干扰温度约束等价转化到Lagrange目标函数中,消除其影响,并提出一种最优干扰对齐算法.该算法采用交替迭代的方式,首先针对与干扰温度约束无关的接收干扰子空间矩阵加以求解,利用 Rayleigh-Ritz定理,直接得到相应的最优迭代关系;然后为了求解相互耦合的发送预编码矩阵,利用凸优化理论中Lagrange对偶原理,将频谱共享问题转化为易处理的两个Lagrange子优化问题,并结合次梯度投影法推导了Lagrange变量的更新关系;最后,理论分析和蒙特卡洛仿真验证了算法的有效性,结果表明所提算法可快速收敛,且获得的速率和性能优于已有的干扰温度类算法[8],可有效实现干扰网络速率和最大化.

2　系统模型与问题描述

2.1系统模型

本文设置的认知MIMO干扰网络 underlay频谱共享模型[9],如图1所示.为了便于分析,考虑只有一对主用户通信的情况(多主用户情况可以通过简单拓展得到),其发射机和接收机分别配备M0和N0个天线,信道传输矩阵为H00∈N0×M0,PU在其授权频率上同时传输d0路数据,即自由度为d0;而次用户网络由典型的K用户MIMO干扰网络构成,其中发射机k和接收机k分别配备Mk和Nk个天线,使用dk个自由度,对应的信道传输矩阵为Hkk∈Nk×Mk(k=1,2,…,K).此外,SU发射机l到接收机k的干扰信道用矩阵Hkl∈Nk×Ml(k≠l)表示,而对于SU发射机l对PU接收机的干扰信道用G0l∈N0×Ml表示.不妨假设信道满足块衰落(blockfading)特性,且矩阵元素服从复高斯分布.

SU和PU分别发送数据sk(k=1,…,K)和s0,经相应预编码Vk、V0及相应信道到达接收机的接收信号yk和y0分别为:

(1)

(2)

2.2问题描述

次用户网络为了实现网络信息速率和最大化,需要网络中各个SU的预编码矩阵Vl和干扰抑制矩阵Uk满足如下干扰对齐(IA)条件来避免相互干扰:

(3)

(4)

文献[12]针对MIMO干扰网络,通过实际干扰信号空间与接收端预设的干扰空间之间矩阵距离来刻画空间的重合程度,从而将干扰对齐的求解等价转化为如下优化问题:

(5)

(6)

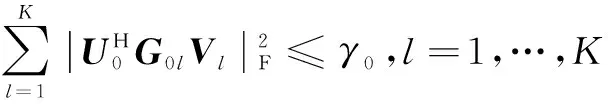
(7)

(8)

(9)

3　最优干扰对齐算法

原优化问题是一个QCQP问题[13],由于干扰温度约束的存在,导致SU发送预编码矩阵Vl互相耦合,无法直接采用传统IA算法求解,属于NP-Hard(Non-deterministic Polynomial-Hard)问题[9].本文采用交替迭代的方式更新Vl和Ck,且该迭代方式可得到最优解[12].

3.1干扰子空间矩阵的更新

固定矩阵Vl求解Ck,此时约束关系式(7)～(8)自然满足,则原问题可进行如下化简,得到如下问题:

(10)

其中,tr (A)表示矩阵A的迹.

则次用户k接收干扰子空间Ck为:

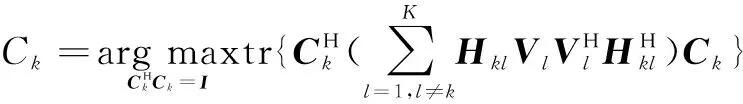
∀k=1,…,K

(11)

由Rayleigh-Ritz定理[14]得:

(12)

3.2预编码矩阵的更新

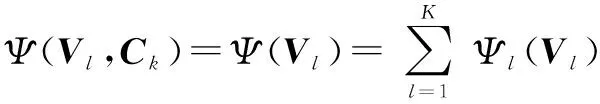
(13)

其中l=1,…,K.上述问题Vl相互耦合,无法直接利用Rayleigh-Ritz求解.通过Lagrange部分对偶[16],将干扰温度约束等价转化到目标函数中,得到如下Lagrange函数[13]:

(14)

其中λl为Lagrange变量.

则对偶函数[13]为:

(15)

其中inf表示下确界,对偶函数Γl(λl)是关于λl的凸函数[13].

Lagrange对偶问题[13]为:

s.t.λl≥0

(16)

3.2.1对偶函数求解问题

对于任意给定Lagrange变量λl(l=1,…,K),对偶函数求解的求解类似于3.1节的求解,推导如下:

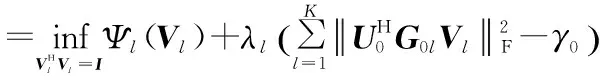
(17)

则

(18)

3.2.2求解Lagrange对偶问题

由于Lagrange对偶问题中的目标函数Γl(λl)是关于λl的仿射函数族的下确界,则Γl(λl)关于λl是不可微的,导致基于梯度的方法(如最速下降法、牛顿法等)无法用于该问题的求解[13],而目标函数表达式比较复杂,难以采用上/下界缩放类方法求解[15],因此本文采用次梯度的方法.在求解前,需要确定目标函数Γl(λl)的次梯度,结合命题1给出求解方法

(19)

(20)

由式(22)减去式(21)得

(21)

而对于凸函数Γl(λl),l=1,…,K,如有如下不等式成立,则称grad(λl)为Γl(λl)在λl点处次梯度[13,16]:

(22)

综上所述,原命题得证.

根据命题1可以得到基于次梯度投影法[16]的λl迭代关系:

(23)

3.3算法主要流程

综上所述,本文所提最优干扰对齐算法的主要流程如算法1:

算法1最优干扰对齐算法

步骤1初始化:设置SU预编码矩阵Vl(0)=[e1,e2,…,edk],l=1,…,K;

步骤2更新干扰子空间矩阵:由式(14)计算SU接收干扰子空间矩阵Ck(n),k=1,…,K;

步骤7结束判断:由式(8)计算目标函数Ψ(Vl,Ck),若Ψ(Vl,Ck)<φ0或n>Nmax,则算法结束;否则返回步骤2.

其中ei表示单位列向量,n表示第n次交替迭代,Nmax为最大交替迭代次数,ε为控制Lagrange变量更新精度的常数,φ0为控制算法精度的常数.

3.4算法有效性分析

命题2当dk(k=1,…,K)一定时,如果IA条件存在可行解,则所提算法可得到一组最优的Vl和Ck,且与初始值无关.

证明首先,对于任意给定初值,算法每次迭代目标函数单调下界,且取值非负(范数平方和形式),因此算法必然收敛.然后,当IA条件存在可行解时,即存在最优的Vl,Ck使Ψ{Vl,Ck}达到极小值.由于Ψ{Vl,Ck}是可微函数,其极值点必定是驻点,即该点处偏导为0:

(24)

(25)

将式(24)和式(25)代入式(6)有Ψ{Vl,Ck}=0,则Vl,Ck分别为当前dk(k=1,…,K)条件下最优预编码矩阵和干扰子空间矩阵[19].

4　仿真结果及分析

为了验证所提算法的有效性,现对算法进行计算机仿真.仿真中假设次用户网络中有三对SU共享频谱(K=3),各配有M副天线,每对SU采用dk(k=1,2,3)个子流传递信息;在同一时刻同一频段上只有一对PU接入,其收发天线数均为N,采用d0个子流传输数据.为了方便分析且不失一般性,不妨设M=6,N=4,d0=2.无线网络的自由度(Degrees of Freedom,DoF)是指网络中无干扰的信号维度,即为独立的发送子流数,利用DoF可以估计多天线所带来的系统容量增益.而且当信噪比较高时,这种估计精确接近100%[20].在上述仿真场景下,当无PU存在的情况下,次用户网络最大可获得的自由度为KM/2=9(其中K为次用户对数目)[8];当有PU存在的情况下,采用正交投影的方法,次用户网络最大可获得的自由度为K(M-d0)/2=6[8].DoF的分配方案会直接影响网络可达速率,为此介于有/无PU存在的最大自由度之间,选取的自由度分配方案(d1,d2,d3)集合为(2,2,2)、(3,2,2)、(2,3,3)和(3,3,3),简记为方案1～4.

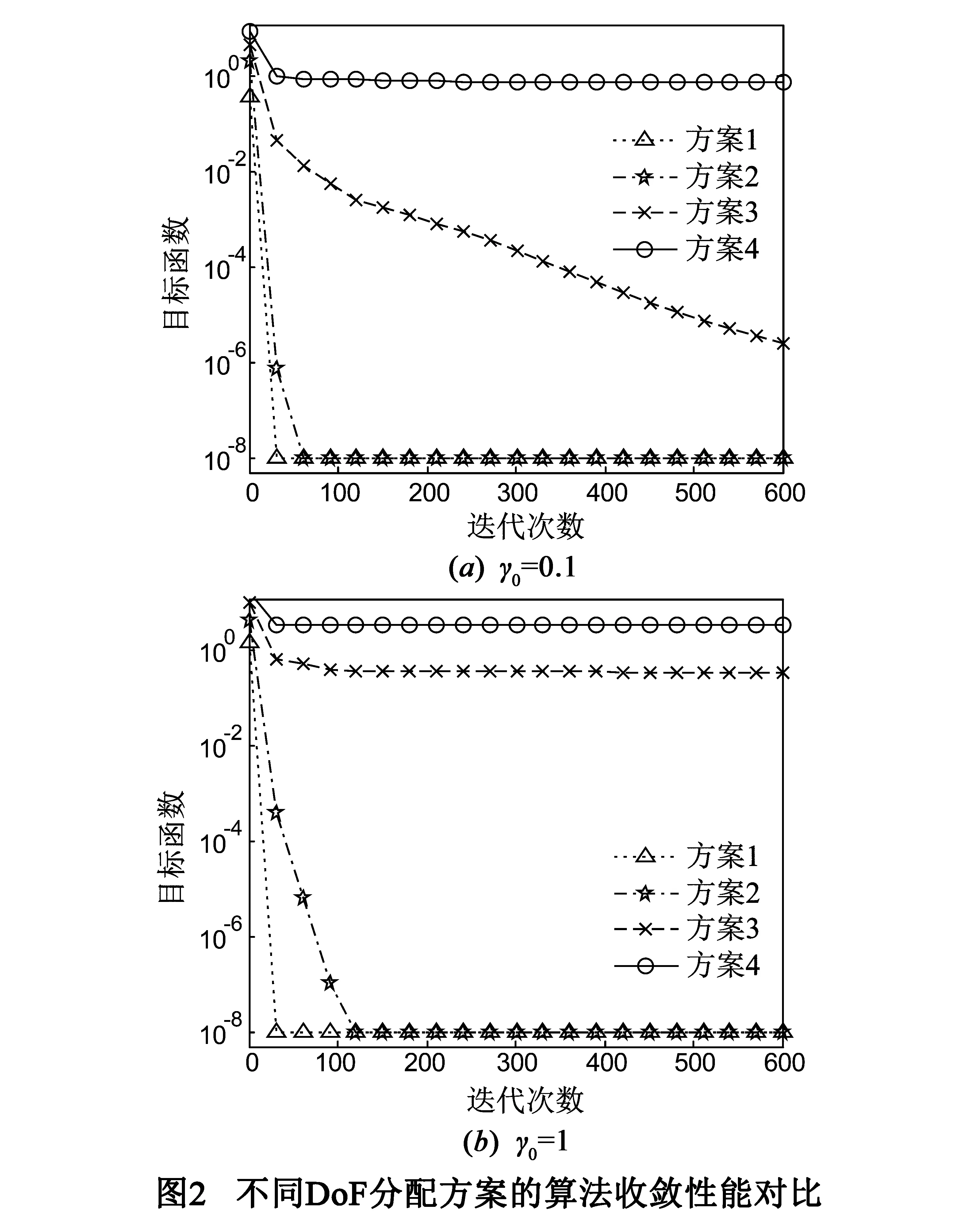
图2在一定的干扰温度设置下,对比了不同DoF分配方案算法收敛性能.仿真结果说明,当采用方案1时,由于存在足够的剩余空间来同时满足抑制SU干扰,目标函数能够快速下降,最终受软件精度限制而终止.随DoF总数增加,算法的收敛性能变差.这是由于DOF总数增加,使得期望信号占用的信号空间增加,而留给抑制各类干扰用的空间减少,对算法实现干扰抑制的要求越来越苛刻,加大了其收敛的难度.对比图2(a)和图2(b)可知,随着干扰温度值得变大,放宽了SU对PU干扰抑制效果的限制,降低了部分要求.因此相同的DoF分配方案下,图2(b)比图2(a)中算法有更好的收敛性能.

图3给出了不同DoF分配方案下次用户网络最大速率和随信噪比的变化曲线.仿真结果说明,在低信噪比下,网络方案的DoF总数越多,其算法可达速率和越大.此时虽然次用户间存在较大干扰,但相对于噪声可忽略,对可达信息速率影响小.而随着信噪比的提高,干扰在信干噪比中所占比例变大,影响逐渐显著,导致速率和趋于饱和.此外,对比仿真图3(a)、3(b),随着干扰温度门限的提高,速率和的饱和门限也随之提高,使得不同方案之间速率和关系可能发生变化.因此,需要根据信噪比和干扰门限的取值,合理选择DoF分配方案来获得最大速率和.

图4给出了本文所提最优IA算法和文献[9]所提SDR-IA算法在不同信噪比下的网络可达最大速率和.所提算法和SDR-IA算法均属于干扰温度类算法,但是相同γ0设置下,仿真结果表明所提算法可达速率和高于SDR-IA算法.这是由于SDR-ITIA算法为了方便求解,采用半正定松弛方式,忽略了对收发优化矩阵的秩约束,求得结果是最优收发矩阵的估计,多子流情况下存在估计偏差.而所提算法通过部分对偶等价转换干扰温度约束,且满足Slater条件,不存在最优对偶间隙,即理论上不存在估计偏差,所以算法性能要优于SDR-IA算法.

为了进一步说明所提算法的最优性能,将其与已有传统最优IA算法的可达速率和进行比较,如图5所示.已有算法的应用场景相当于与本文应用场景的一个特例,其中分布式IA算法是针对MIMO干扰网络(无PU存在)提出的,无需考虑对PU干扰约束限制,相当于γ0=+∞的情况,可作为underlay方式最优算法最大速率和上界;ICIA算法针对认知MIMO干扰网络overlay方式提出,要求完全消除对PU干扰,相当于γ0=0的情况,这种正交投影算法在高信噪比下可作为underlay方式最优算法最大速率和下界[18].仿真结果说明,本文算法可达的最大速率和高于ICIA算法,且随着干扰温度门限γ0的增加,最终趋于分布式IA算法,说明所提算法的有效性,可实现网络速率和最大化,从而进一步验证了理论分析的结果.

5　结束语

针对认知干扰网络underlay频谱共享问题,采用Lagrange部分对偶,等价转换干扰温度约束,提出一种最优IA算法.理论分析和仿真结果表明:一方面,DoF分配方案会直接影响网络的速率和性能,要根据接收信噪比和干扰温度门限进行合理规划;另一方面,所提最优迭代算法可达的最大速率和高于已有underlay 方式SDR-IA算法,且介于无PU干扰的分布式IA算法和overlay方式的ICIA算法之间,可实现网络速率和的最大化.

[1]HAYKIN S.Cognitive radio:brain-empowered wireless communications[J].IEEE Journals on Selected Areas in Communications,2005,23(2):201-220.

[2]KHOSHKHOLGH M G,NAVAIE K,YANIKOMEROGLU H.Access strategies for spectrum sharing in fading environment:overlay,underlay,and mixed[J].IEEE Transactions on Mobile Computing,2010,9(12):1780-1793.

[3]荣玫,朱世华,李锋.认知无线电网络基于F范数的频谱共享[J].电子学报,2011,31(1):95-100.

RONG M,ZHU SH H,LI F.Spectrum sharing based on Frobenius norm in cognitive radio networks[J].Acta Electronica Sinica,2011,31(1):95-100.(in Chinese)

[4]LEE D,JEONG B J.Performance analysis of scheduled cognitive radio systems with MIMO transmission[J].IEEE Transactions on Vehicular Technology,2013,62(8):4088-4093.

[5]LI C,SUN F,CIOFFI J,et al.Energy efficient MIMO relay transmissions via joint power allocations[J].IEEE Transactions on Circuits and Systems-II,2014,61(7):531-535.

[6]EL-ABSI M,SHAAT M,BADER F,et al.Interference alignment based resource management in MIMO cognitive radio systems[A] 20th European Wireless Conference[C].Barcelona:VDE Press,2014.1-6.

[7]GOMADAM K,CADAMBE V R,JAFAR S A.A distributed numerical approach to interference alignment and applications to wireless interference networks[J].IEEE Transactions on Information Theory,2011,57(6):3309-3322.

[8]AMIR M,ELKEYI A,NAFIE M.Constrained interference alignment and the spatial degrees of freedom of MIMO cognitive networks[J].IEEE Transactions on Information Theory,2011,57(5):2994-3004.

[9]DU H,RATNARAJAH T,ZHOU H,et al.Interference alignment for peer-to-peer underlay MIMO cognitive radio network[A].2011 Conference Record of the Forty Fifth Asilomar Conference[C].Pacific Grove:IEEE Press,2011.349-353.

[10]LUO Z,MA W,SO A M C,et al.Semidefinite relaxation of quadratic optimization problems[J].IEEE Signal Processing Magazine,2010,27(3):20-34.

[11]Zhang Y J A,So A M C.Optimal spectrum sharing in MIMO cognitive radio networks via semidefinite programming[J].IEEE Journal on Selected Areas in Communications,2011,29(2):362-373.

[12]PETERS S W,HEATH R W.Interference alignment via alternating minimization[A].IEEE International Conference on Acoustics,Speech and Signal Processing[C].Taipei:IEEE Press,2009.2445-2448.

[13]Boyd S,Vandenberghe L.Convex Optimization[M].UK:Cambridge University Press,2009.208-223.

[14]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.528-548.

ZHANG X D.Matrix Analysis and Applications[M].Beijing:Tsinghua Press,2004.528-548.

[15]LI C,WANG X,YANG L,et al.A joint source and relay power allocation scheme for a class of MIMO relay systems [J].IEEE Transactions on Signal Processing,2009,57(12):4852-4860.

[16]魏飞,杨震.认知 MIMO MAC 最优迭代注水算法[J].通信学报,2012,32(11):133-139.

WEI F,YANG Z.Optimum iterative water-filling algorithm for cognitive MIMO MAC[J].Journal on Communication,2012,32(11):133-139(in Chinese).

[17]BOYD S,XIAO L,MUTAPCIC A.Subgradient Methods[EB/OL].http://www.stanford.edu/class/ee392o,2003-11-16/2006-07-01.

[18]ZHANG R,LIANG Y C.Exploiting multi-antennas for opportunistic spectrum sharing in cognitive radio networks[J].IEEE Journal of Selected Topics in Signal Processing,2008,2(1):88-102.

[19]WU Y,ZHANG J,ZHOU S,et al.Precoding in the multiuser MIMO downlink based on subspace tracking techniques[A].2005 IEEE 62nd Vehicular Technology Conference[C].Dallas:IEEE Press,2005.2382-2386.

[20]HUANG C,JAFAR S A.Degrees of freedom of the MIMO interference channel with cooperation and cognition[J].IEEE Transactions on Information Theory,2009,55(9):4211-4220.

朱世磊男,1987年生于江苏淮安.现为解放军信息工程大学导航与空天目标工程学院博士研究生.主要研究方向为MIMO无线通信、认知无线电频谱共享、预编码和干扰对齐技术.

E-mail:zhushilei3620@163.com

郑娜娥女,1984年生于福建漳州.现为解放军信息工程大学导航与空天目标工程学院博士、讲师.主要研究方向为MIMO信号处理和无线资源分配.

E-mail:13837122426@163.com

巴斌男,1987年生于河南周口.现为解放军信息工程大学导航与空天目标工程学院博士研究生.主要研究方向为通信系统与信号处理.

E-mail:xidianbabin@163.com

胡捍英男,1961年生于河南内乡.现为解放军信息工程大学教授、博士生导师.主要研究方向为无线通信和空间信息技术.

E-mail:huhanying@vip.sina.com

Optimum Interference Alignment Algorithm for Cognitive MIMO Interference Network

ZHU Shi-lei,ZHENG Na-e,BA Bin,HU Han-ying

(InstituteofNavigationandSpaceTargetEngineering,InformationEngineeringUniversity,Zhengzhou,Henan450000,China)

Cognitive radio can improve the spectrum efficiency by fusing with technologies such as multi-input multi-output (MIMO),orthogonal frequency division multiplexing (OFDM),ultra wideband (UWB),cooperative communication,etc.Cognitive MIMO is a fusion technology of cognitive radio and MIMO,which has advantages of interference suppression,anti-multipath fading,spatial diversity,and multiplexing.However,there is intercoupling among its precoding matrices because of the interference temperature constraint in underlay sharing mode,which makes it difficult for the cognitive MIMO in the underlay interference network to obtain optimal transmitting performance.Consequently,an optimal interference align algorithm for cognitive MIMO interference network is proposed to obtain the optimized interference network transmitting performance,in which the iteration relationship between the optimal transmitting and receiving matrices is derived by interactively and alternately using transmitting precoding and receiving interference subspace matrix,and the derivation process is based on Rayleigh-Ritz theorem and convex optimization theory.In order to remove the interference temperature constraint,the Lagrange partial of dual-decomposition was exploited,and the sub-gradient projection method was adopted to update the Lagrange variable,which overcame the shortcoming of decreasing transmitting rate caused by ignorance of the matrix rank constraint in the existing semi-definite relaxation algorithms.The validity of this algorithm is verified by theoretical analysis and numeric simulations,and results also indicate that the proposed algorithm is capable of maximizing the cognitive MIMO interference network available transmitting rate.

cognitive multi-input multi-output (MIMO); underlay spectrum sharing; interference network; interference alignment; Lagrange partial dual

2014-12-17; 修回日期:2015-03-30;责任编辑:覃怀银

国家科技重大专项(No.2011ZX03003-003-02); 国家863计划项目(No.2012AA01A502,No.2012AA01A505)

TN92

A

0372-2112 (2016)06-1406-07