GTD模型参数估计的时域稀疏成分分析法

钟金荣，文贡坚

(国防科技大学ATR重点实验室，湖南长沙 410073)



GTD模型参数估计的时域稀疏成分分析法

钟金荣，文贡坚

(国防科技大学ATR重点实验室，湖南长沙 410073)

准确高效地估计GTD模型参数对目标特性研究和目标识别有重要的意义.本文根据雷达宽带时域信号能量集中的特点，建立稀疏成分分析的时域模型，实现GTD模型参数估计.该时域模型，根据高分辨率一维像自适应地缩小散射中心分布的可能区域，缩减字典的列数；利用GTD模型的时域响应构建时域字典，并截断字典中值较小的元素使字典成为稀疏矩阵.根据模型的特点设计了一个基于正交匹配追踪的求解方法.与现有频域模型相比，时域模型的字典不但维数减少而且是一个稀疏矩阵，能极大地降低字典的数据量和模型求解计算量.通过实验验证了时域字典的性能和参数估计方法的有效性.

GTD模型；参数估计；稀疏成分分析；时域稀疏；

1　引言

光学区雷达目标可由几个等效散射中心表示，基于几何绕射理论(Geometrical Theory of Diffraction,GTD)的散射中心模型[1]，能够准确描述雷达目标特性，与几何结构有对应关系，受到了广泛的关注和重视.从雷达宽带测量数据中估计目标散射中心GTD模型的参数，对目标识别有重要的意义.

GTD模型包含位置参数，幅度参数和离散的类型参数，无法采用谐波参数估计等经典信号参数估计方法.Potter等提出了GTD模型参数的最大似然方法，需要求解包含混合参数的高维非线性非凸优化问题[1]，求解难度大、初值要求高，而极大似然方法类方法的研究[2]集中在放宽初值的要求或提高优化求解效率.

稀疏成分分析[3,4]利用信号在特定变换域上的稀疏性，从过完备向量集中选择尽量少的分量表示已知信号，能够提取信号中的主要信息.基于雷达信号具有稀疏性[3～7]这一事实，杜小勇等提出了基于频域稀疏成分分析的GTD模型参数估计方法[3]，将参数估计问题转化为一个信号选择问题，不要求准确的初值和复杂的模型定阶，且GTD模型的离散类型参数非但不会对参数估计造成困扰反而有利于参数估计.字典构造是稀疏成分分析法的关键，GTD模型形式复杂，导致字典维数较高，从而带来存储量和计算量上的巨大挑战.

值得注意的是，宽带雷达时域信号能量集中；GTD模型的时域响应是sinc形函数，能量主要分布在主瓣附近.根据此特点，本文提出在时域构造字典和求解的稀疏成分分析方法.该方法采用两种措施降低字典规模，克服字典维度过高的问题.第一，截断一维距离像的小值区域，缩小散射中心分布的可能区域，减少字典矩阵的列数.第二，利用GTD模型的时域响应构建字典并截断字典的小值元素，使字典成为一个稀疏矩阵.时域字典的所需的存储量显著降低.此外，为了防止新字典重构信号时产生误差，本文以正交匹配追踪法为基础设计了重构方法.最后，通过实验验证了本文方法的有效性.

2　信号模型

设雷达发射步进频率信号，起始频率f0，频率步进Δf，步进点数为M，带宽B=M·Δf.第m个频点的采样值为D(fm)=E(fm)+V(fm)，其中，fm=f0+mΔf，m=0,1,…,M-1.E(fm)是目标真实的频域响应，V(fm)是噪声.高频区，E(fm)可由几个等效散射中心的响应合成[1]

(1)

其中，E(fm;Θ)是E(fm)的参数化表示，Θ是目标所有散射中心的参数集，Θ={Θ1,…Θp…,ΘK},K表示散射中心的数目.Θp是第p个散射中心的参数集，Ep(fm;Θp)是散射中心的GTD参数化模型，形式为：

Ep(fm;Θp)=Ap·(jfm/fc)αp·exp(-j4πfmrp/c)

(2)

每个散射中心包含三个参数Θp={Ap,rp,αp}.Ap是散射中心的幅度，rp是散射中的位置，αp是散射中心的频率依赖因子.αp取[-1,-0.5,0,0.5,1]等5个离散值，对应尖顶绕射，边缘绕射，双曲面反射和直边-镜面反射，平板反射，二面角反射等5类几何结构的散射特性.此五段分模型，描述了几何结构散射响应与入射频率的关系，有利于目标特征提取[1]，但离散参数也导致极大似然等估计方法的代价函数不连续，对参数估计造成困扰.

设雷达不模糊距离为S=[-R/2,R/2]，起始点为r0.以间隔Δr将S离散成Nr点，αp取Nα=5个离散值[-1,-0.5,0,0.5,1]，则稀疏向量s的长度为N=Nr·Nα，s=[s0,…,sNr-1,…,s(nα-1)Nr,…,sNrNα-1]T，rn=r0+nrΔr，αn=-1+0.5nα是sn对应的频率依赖因子和距离值,nα=0,…,Nα-1,nr=1,…,Nr-1,n=nαNr+nr.

现有雷达信号稀疏成分分析方法[3]以频域信号作为观测数据，即y=[y0…yM-1]T，ym=D(fm).在频域构造大小为M×N的字典(Frequency-Domain dictionary,FD)Ψ=[ψ0,…,ψn,…,ψN-1]，ψn=[ψ0,n… ψM-1,n]T称为字典的一个原子.每个元素的计算方式为：

(3)

如图1所示，测量数据可由字典的若干原子构成，即：

y=Ψ·s

(4)

3　时域稀疏成分分析参数估计方法

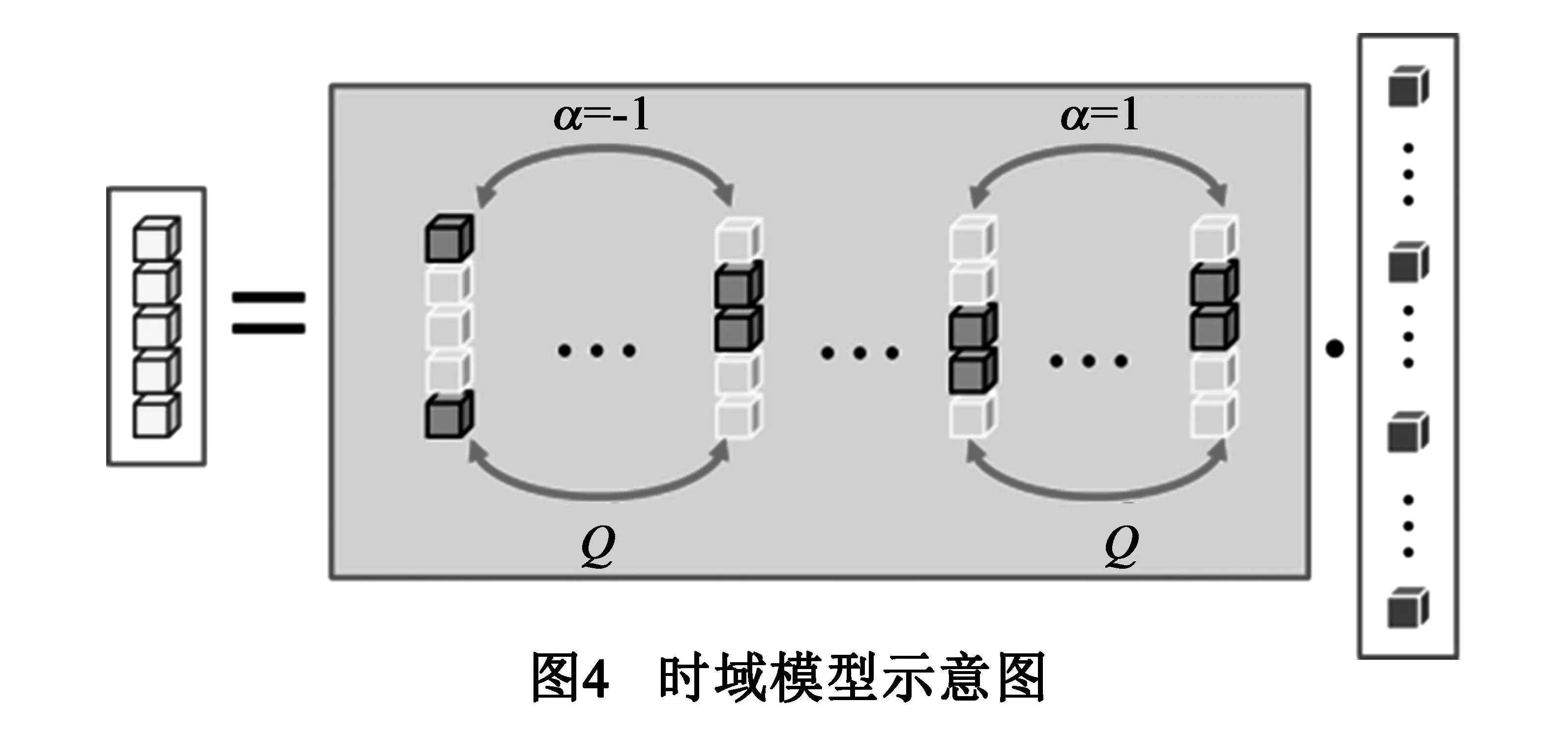
图2给出了雷达信号和字典原子的时/频域波形.分析目标的时域波形发现：散射中心并非在S内的任意位置都存在，一些低能量区域存在散射中心的可能性较小.且考虑到噪声、雷达信号的有效动态范围有限等因素，能量太低的区域通常已经是无效信号.这些区域即使存在散射中心也不可信，对目标识别等后续环节意义不大.利用这一特点可以缩小散射中心分布的区域范围，减少字典的列数.观察时域原子发现：原子的能量集中在主瓣附近.原子的自相关、原子之间的互相关，主要贡献都来自于这一区域，其它区域的产生影响较小.本文根据上述两个特点，构造GTD模型时域字典(Time-domain Dictionary,TD)，降低字典的维度和数据量.

为讨论方便，定义傅里叶变换算子IFFT(·,·).若A是向量，IFFT(A,L)表示对A进行L点的傅立叶逆变换；若A是矩阵，IFFT(A,L)表示对A的每一列进行L点的傅立叶逆变换.省略L，则IFFT(A)表示傅立叶变换点数和原数据长度相同.

3.1缩小值域

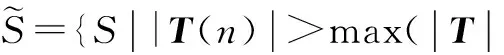
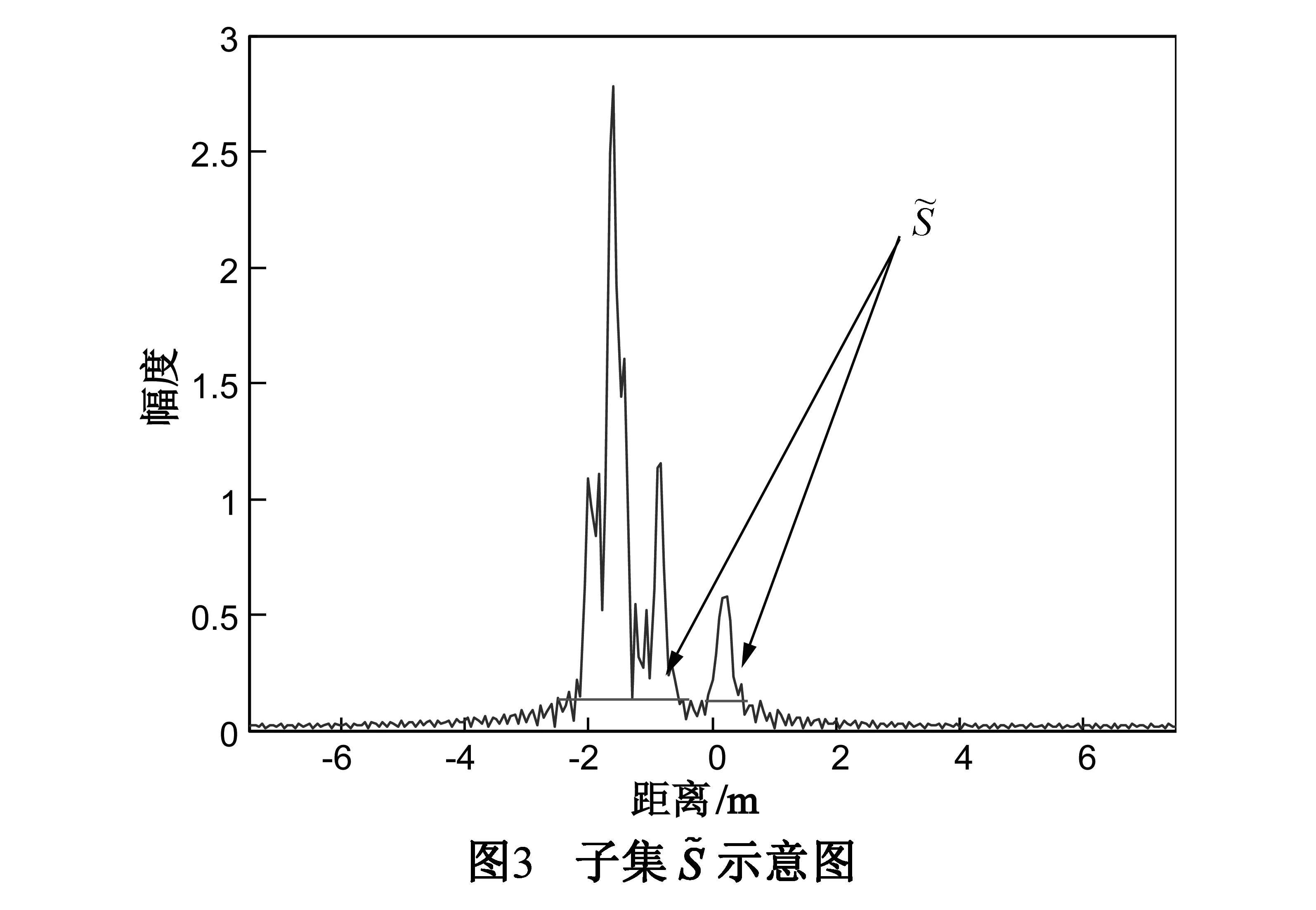
3.2构建时域字典

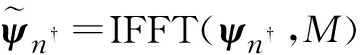
(5)

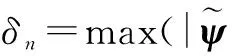
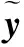
(6)

s*是长度为N†=Q×Nα的目标向量.

3.3时域成分分析模型

实际观测数据存在噪声，式(6)的问题变为：

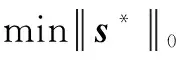
(7)

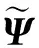
4　求解方法

本文基于正交匹配追踪法[8]设计求解方法，求解式(7)的l0范数优化问题.向量s和s*都由此方法求解，为简洁起见统一用s表示.基本步骤如下：

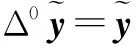
步骤1选择式(8)值最大的一个原子nk，Re(·)为取实部操作.然后，更新支撑集Fk=Fk∪nk.

(8)

(9)

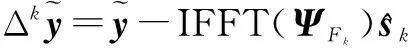
步骤3令k=k+1，重复步骤1直到满足停止条件：

(10)

5　性能分析

模型的性能包括三方面：字典数据量，参数估计的稳定性，参数估计精度.

(1)字典数据量λ.其定义如下：

(11)

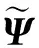
(2)字典最小自相关系数.关于字典的求解难度和风险的评价问题，被广泛认可的是约束等距性(Restricted Isometry Property,RIP)原理，但RIP计算难度大，通常可用最大相关系数替代(Maximum Correlation，MC)[9].

(12)

ψi是第i个原子.μ越小重构稳定性越好.

(13)

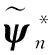
(4)重构信号的误差和相关系数.评价估计精度，最直接的方法是与真值比较.参数真值未知时，可比较重构信号与原信号的相对误差ηx和相关系数μx：

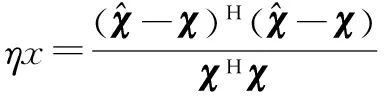
(14)

6　实验结果

首先，分析第5节定义的字典的性能指标.然后，运用本文的方法从仿真数据和目标暗室数据中估计目标散射中心参数，分析参数估计和重构信号的精度，验证本文方法的有效性和准确性.时域字典稀疏矩阵采用Matlab的sparse函数存储.

6.1截断对字典的影响

6.1.1Δr=0.15m时字典性能

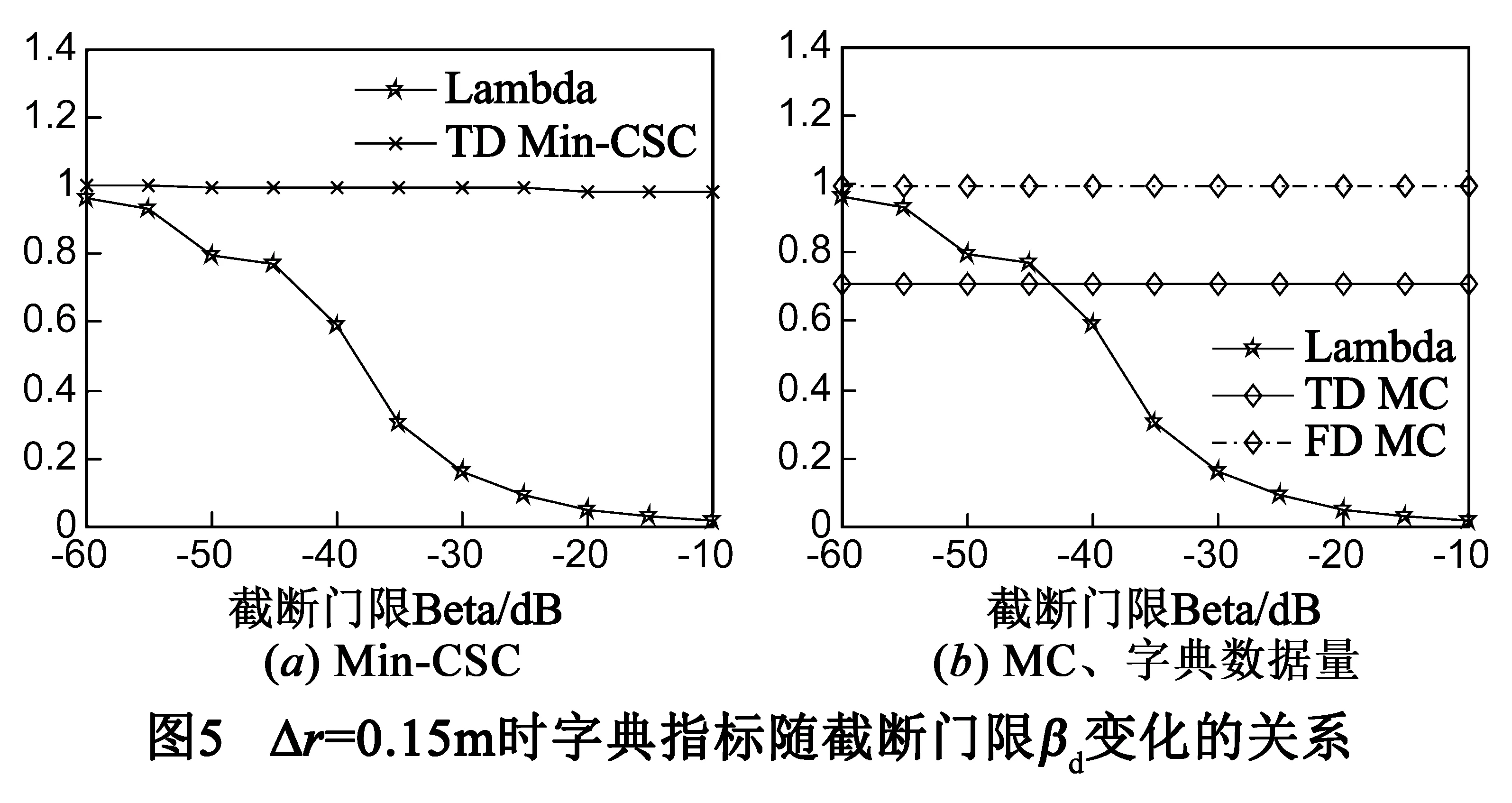
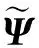
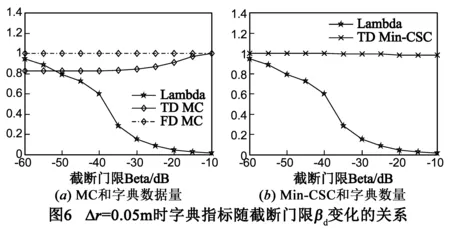
6.1.2Δr=0.05m时字典性能

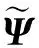
6.2仿真数据参数估计实验结果

仿真目标由五个散射中心组成，散射中心参数如表1所示.雷达系统参数与6.1节一致，加入高斯白噪声使信噪比SNR=30dB，βs=-30dB.

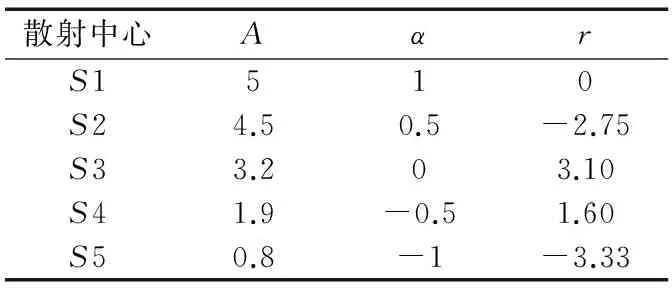
表1　仿真目标散射中心参数设定

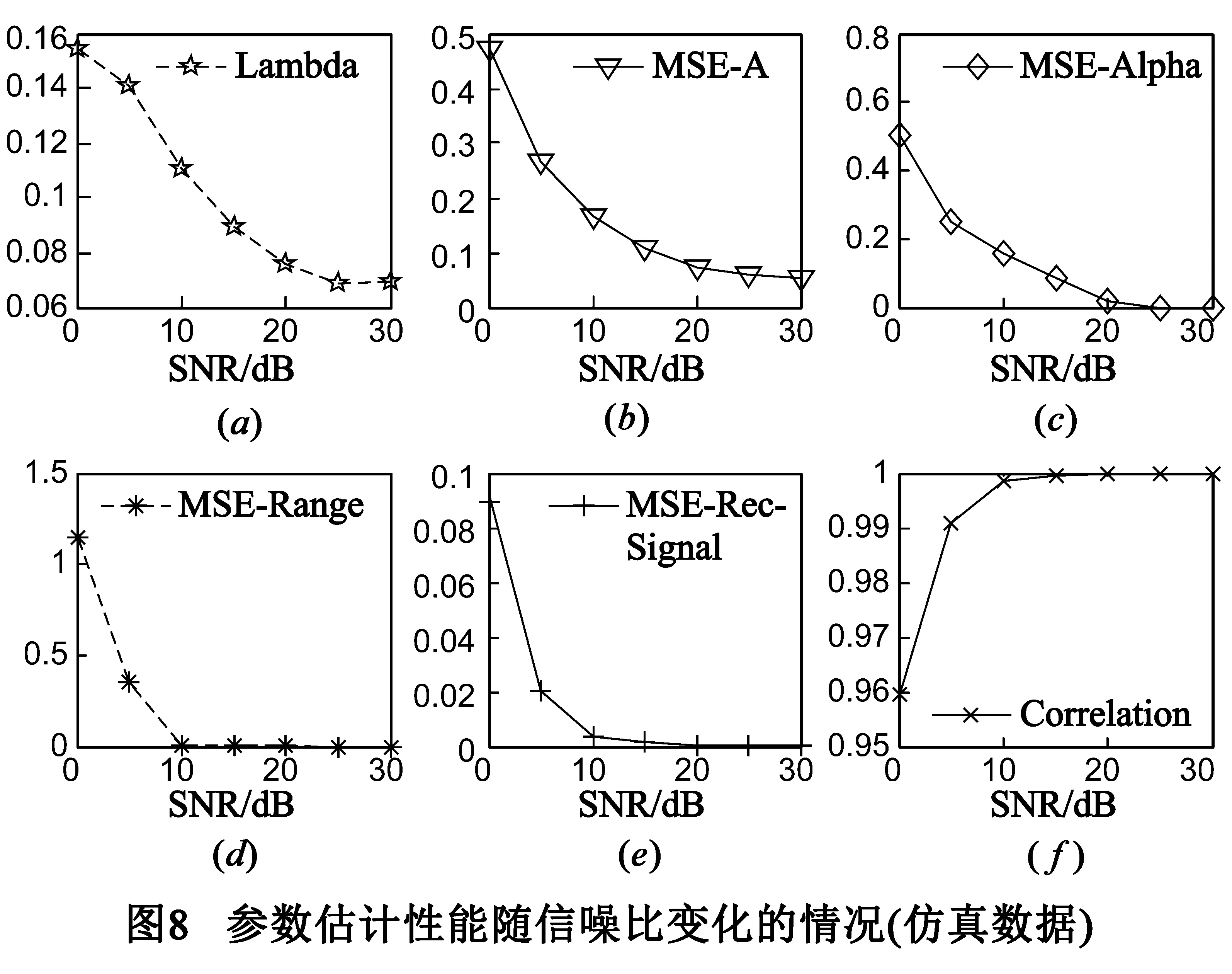
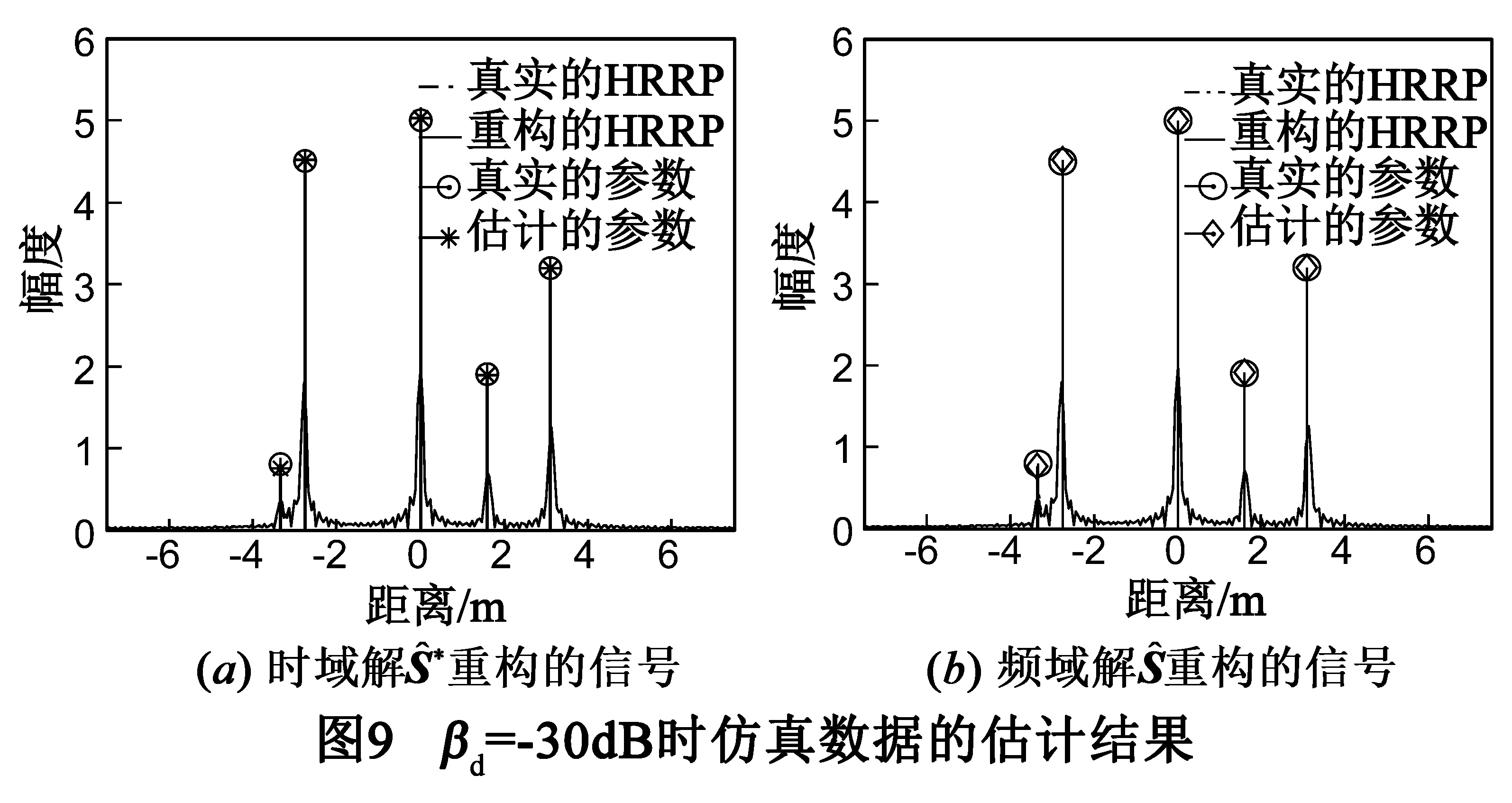
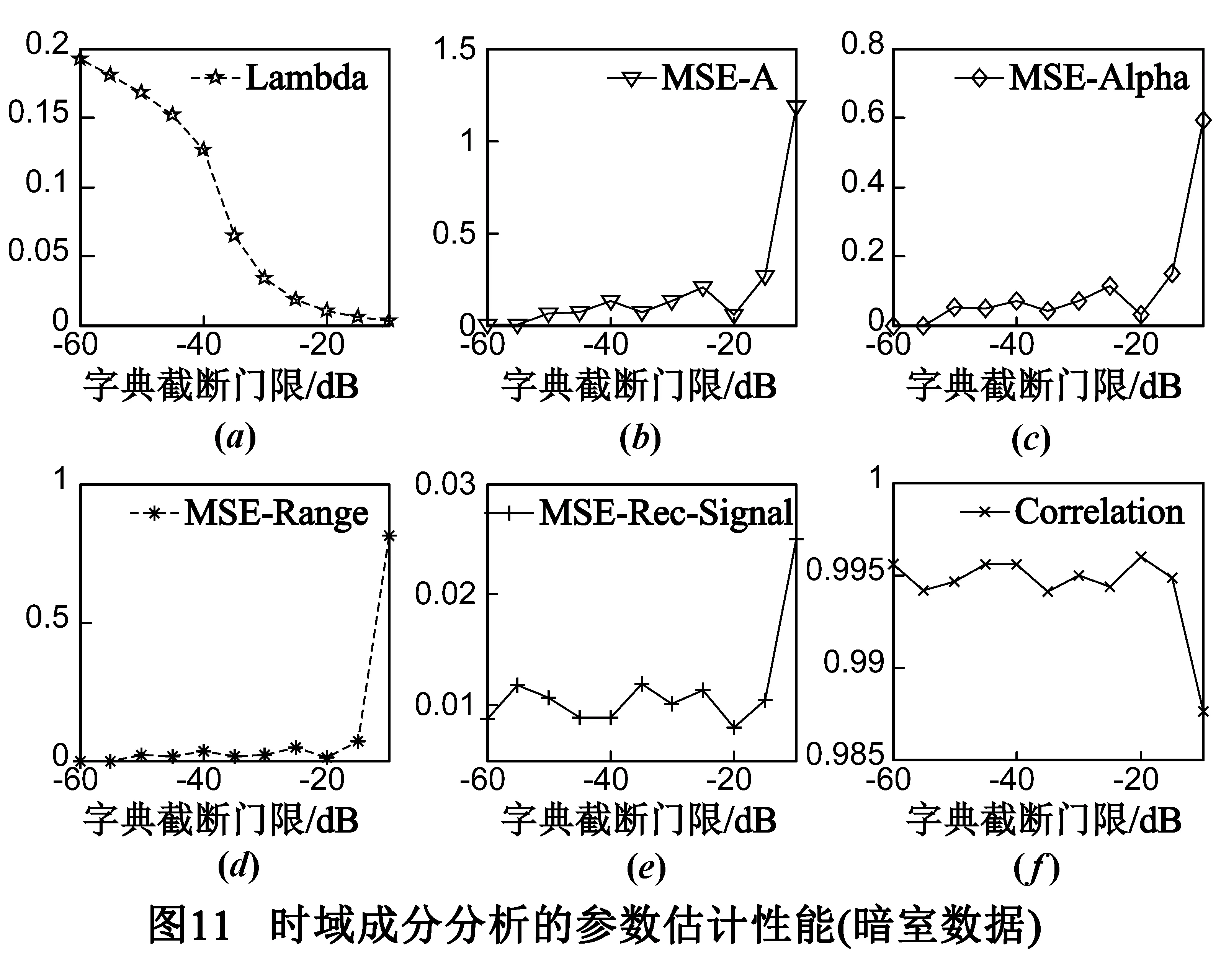
信噪比下降对参数估计造成两个影响:(1)参数估计精度下降，尤其是幅度参数和频率依赖因子的估计精度受到的影响较大.SNR=10dB时，估计误差仍然处于可以接受的水平；SNR≤5dB时，估计误差，特别是位置参数估计误差增大较为明显，原因在于幅度较低的散射中心被掩盖，虚假散射中心的出现概率较大；(2)时域字典的数据量增加，如图8(a)所示.时域字典采用了两个措施来缩减字典的数据量，一是根据一维距离像缩减散射中心可能分布的区域，减少字典的列数；二是截断GTD模型时域响应的低能量区域，使字典成为二维稀疏矩阵.若信噪比较低(如SNR=0dB),而信号截断门限βs不变，一些噪声区域会被判别为可能存在散射中心的区域，使字典的列数增加、字典数据量增大.但是，无论信号噪声如何变化，第二个措施是不受影响的.时域字典仍然是稀疏矩阵，字典数据量仍然明显下降.

表2　SNR=30dB、βd=-30dB时，参数估计结果

6.3暗室数据实验结果

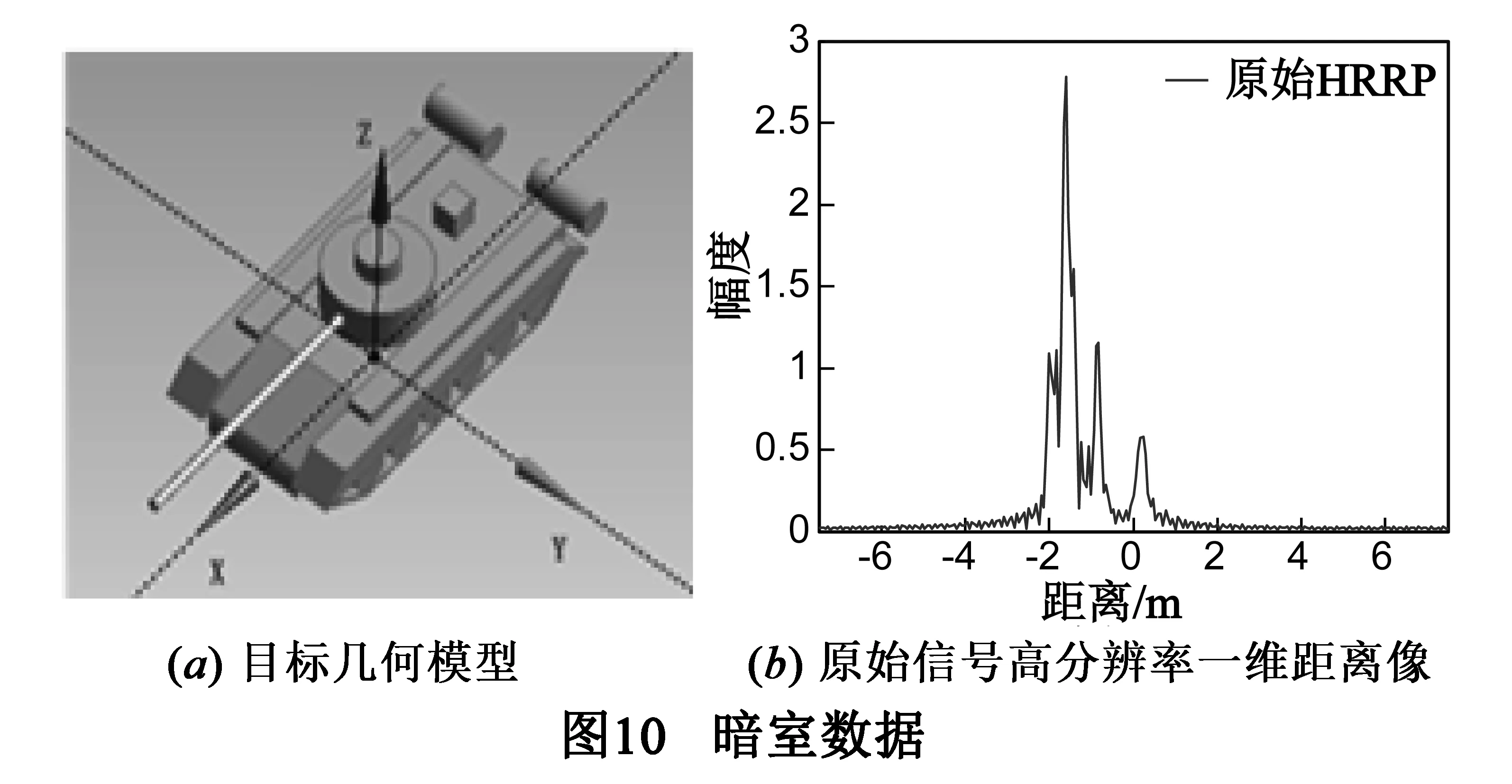
目标的CAD模型如图10(a)所示，实验数据为1/4缩比暗室测量，传感器测量位置位于目标的高度角30°，方位角87.5°处(方位角定义为X轴正向逆时针转动的角度)，发射频率f:34～38GHz，频率步进Δf=40MHz.测量数据的一维距离像如图10(b)所示.稀疏度设为K=10，其它参数与6.2节相同.由于目标散射中心参数真值未知，而频域稀疏方法参数估计的有效性和准确性已经被众多文献验证[3]，因此将时域方法的参数估计结果与频域方法的结果进行对比.

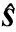
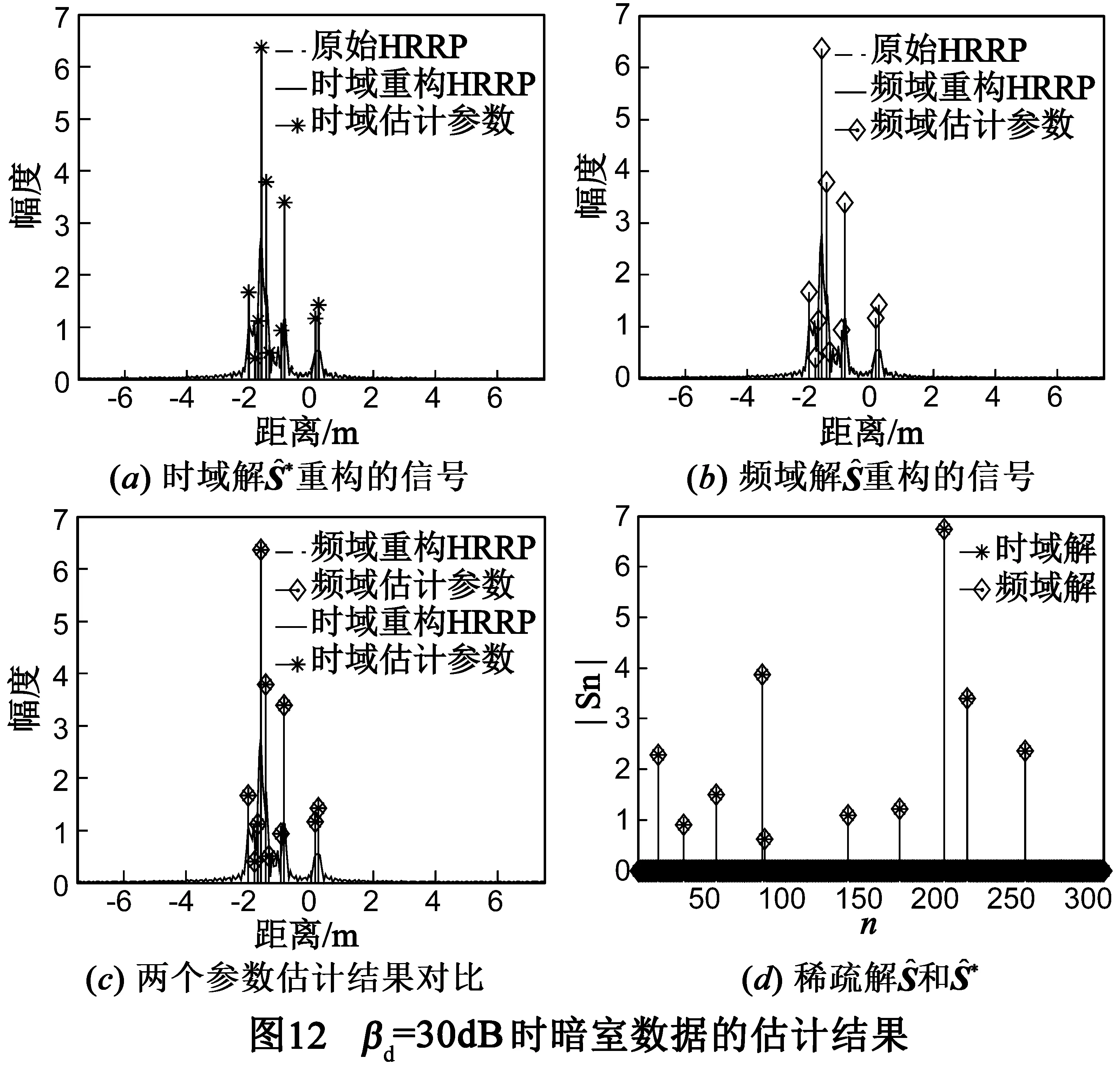
7　结论

本文紧紧抓住雷达目标时域信号和GTD模型时域响应能量聚集的特点，提出了GTD模型参数估计的时域成分分析法.该方法根据雷达信号的时域波形，限制了散射中心可能分布的区域，减少字典的维度(列数)；利用截断的散射中心GTD模型时域响应构造字典.时域字典相比频域字典不但维度减少而且是稀疏矩阵，能够极大地降低字典数据量.稀疏成分字典规模的降低，还有利于降低稀疏成分分析模型求解的计算量.文中还根据新字典的特点，给出了以正交匹配追踪法为基础的模型求解方法.实验结果表明了时域稀疏成分分析字典和稀疏表示信号模型的有效性.

本文的时域稀疏成分分析模型具有很强的普适性，现有的雷达一维信号频域稀疏表示方法很大一部分都能够类似地转换到时域以降低字典规模.更高维度的散射中心模型[10]时域响应也有能量聚集的特点，因此时域稀疏方法可推广至二维/三维雷达成像或参数估计.

[1]Potter L C,Chiang D M,Carriere R,el al.A GTD-based parametric model for radarscattering[J].IEEE Trans Antennas and Propagation,1995,43(10):1058-1066.

[2]石志广,周剑雄,赵宏钟,等.基于协同粒子群优化的GTD 模型参数估计方法[J].电子学报,2007,35(6):1102-1107.

Shi Z G,Zhou J X,Zhao H Z,et al.A GTD Scattering center model parameter estimation method based on CPSO[J].Acta Electronica Sinica,2007,35(6):1102-1107.(in Chinese)

[3]杜小勇,胡卫东,郁文贤.基于稀疏成份分析的几何绕射模型参数估计[J].电子与信息学报,2006,35(2):363-366.

Du X Y,Hu W D,Yu W X.Parameter estimation of GTD model based on sparse component analysis[J].Journal of Electronics Information Technology,2006,28(2):363-366.(in Chinese)

[4]Ausin C D.Sparse Methods for Model Estimation with Applications to Radar Imaging[D].Columbus：The Ohio State University,2012.

[5]邱伟，赵宏钟，周剑雄，等.基于联合稀疏性的高分辨全极化雷达成像研究[J].电子学报，2013，41(9)：1685-425.

Qiu Wei,Zhao Hong-zhong,Zhou jian-xiong,et al.High resolution full polarization radar Imaging based on joint sparsity[J].Acta Electronica Sinica,2013,40(9):1685-1693.(in Chinese)

[6]周汉飞,李禹,粟毅.基于压缩感知的多角度SAR 特征提取[J].电子学报,2013,41(3):543-548.

Zhou Han-fei,LI Yu,Su Yi.Multi-aspect SAR feature extraction based on compressive sensing[J].Acta Electronica Sinica,2013,41(3):543-548.(in Chinese)

[7]Zhang L,Qiao Z J,Xing M D,et al.High-resolution ISAR imaging by exploiting sparse apertures[J].IEEE Trans on Antennas and Propagation,2012,60(2):997-1008.

[8]Donoho D L,Tsaig Y,Drori I,et al.Sparse solution of underdetermined systems of linearequations by stagewise orthogonal matching pursuit[J].IEEE Trans on Information Theory,2012,58(2):1094-1121.

[9]Donoho D L,Elad M,Temlyakov V N.Stable recovery of sparse over complete representation in the presence of noise[J].IEEE Trans Information Theory,2006,52(4):6-18.

[10]Gerry M J,Potter L C,Gupta I J.A parametric modelfor synthetic aperture radar measurements[J].IEEE Trans on Antennas and Propagation,1999,4(7):1179-1188.

钟金荣男，1985年7月生，广西玉林人，现为国防科技大学ATR重点实验室博士研究生，研究方向为雷达目标特性建模，图像处理，自动目标识别.

E-mail:Zhong-nudt@163.com

文贡坚男，1972年8月生，湖南宁乡人，国防科技大学ATR重点实验室教授、博士生导师，研究方向包括图像处理，自动目标识别以及摄影测量与遥感等.

Time Domain Sparse Component Analysis Method for GTD Model Parameter Estimation

ZHONG Jin-rong,WEN Gong-jian

(ATRKeyLab,NationalUniversityofDefenseTechnology,Changsha，Hunan410073,China)

Estimating of geometrical theory of diffraction (GTD) model parameters accurately and efficiently is significant for automatic target recognition.In this paper,a time-domain sparse component analysis method is designed for parameter estimation of GTD model.Firstly,potential locations of scattering centers,as well as columns of the dictionary,are reduced according to the high resolution range profile.Secondly,the time domain responses of GTD model is used to construct the dictionary,and the small amplitude areas are cut off.Compared with the presented method,not only columns of the new dictionary are reduced,but also the dictionary becomes a sparse matrix.As a consequence,it needs less memory to store,which is helpful to decrease computational complexity of component analysis.In addition,a reconstruction method based on the orthogonal matching pursuit is designed for our dictionary.Finally,experimental results demonstrate the performance and efficiency of the proposed method.

GTD model;parameter estimation;sparse component analysis;time domain sparse

2014-09-17；修回日期：2015-10-11；责任编辑：梅志强

教育部新世纪优秀人才支持计划(No.NCET-11-0866)

TN957.52

A

0372-2112 (2016)06-1336-07