空间调制系统低复杂度的天线选择算法

门宏志,刘文龙,王　楠,金明录

(大连理工大学信息与通信工程学院,辽宁大连 116023)



空间调制系统低复杂度的天线选择算法

门宏志,刘文龙,王楠,金明录

(大连理工大学信息与通信工程学院,辽宁大连 116023)

空间调制(Spatial Modulation,SM)是一种特殊的多天线传输技术,利用发送天线索引和发送的符号共同传递信息.为了获得发送分集增益,人们将天线选择技术应用到SM系统中,提高SM系统解调性能.在天线选择技术中,最大-最小欧式距离(Euclidean Distance Antenna Selection,EDAS)准则应用较为广泛,但是它的全搜索求解方法复杂度高,限制了其应用.为此,本文利用空间调制系统和调制符号本身的特性,从2维量化解调的视角出发,给出了两种低复杂度的最优天线选择算法,并通过计算机仿真和复杂度分析,表明了该算法的有效性和最优性.

空间调制;天线选择;低复杂度

1　引言

现代无线通信对数据传输速率和频谱利用率的要求越来越高,多输入多输出(Multiple Input Multiple Output,MIMO)系统应运而生[1].然而,由于信道间干扰(Inter-Channel Interference,ICI),天线间同步(Inter-Antenna Synchronization,IAS)和多无线电射频(Radio Frequency,RF)链路等问题,引起了MIMO系统成本和复杂度的不断增加.空间调制(Spatial Modulation,SM)技术的出现解决了MIMO系统的上述局限.

SM系统解调不同于传统MIMO系统的解调,不仅需要解调发送天线发送的符号,还需要判断是由哪根天线进行发送的.激活天线的解调主要依靠发送天线信道间的差异,所以信道特性对SM系统解调的影响严重,需要尽可能地选择信道特性较好的天线进行数据传输.所以各国学者提出了各种新的空间调制方案,主要包括开环[5～7]和闭环[8～10]两种方案.天线选择技术已经在传统MIMO系统中被广泛研究和应用[11～13],在提高系统性能上有良好效果,所以天线选择技术被引入SM系统,受到学者们的关注.天线选择的一个有效的准则是欧氏距离准则(Euclidean Distance Antenna Selection,EDAS),但全搜索的EDAS算法具有非常高的计算复杂度,限制了其应用.为此,多种低复杂度的次优[14～15]和最优[16～17]天线选择算法相继被提出.

文献[14]的算法认为天线间信道增益矩阵的奇异值越小,其天线间欧氏距离越小.文献[15]的算法认为发送符号的幅度越小,欧氏距离越小,因此只遍历幅度最小的发送符号即可.在文献[16]中,作者提出了一种低复杂度的EDAS(EDAS-LC)算法,利用QR分解和硬判决思想,降低算法的复杂度,同时保持了全搜索EDAS算法的最优性.文献[17]是在文献[16]的基础上,利用调制符号的镜像对称特性,进一步降低天线选择算法的计算复杂度.这两种算法只讨论了MQAM调制的SM系统,没有考虑MPSK调制的SM系统.然而,与非恒包络调制(如MQAM)相比,恒包络调制(如MPSK)能在功耗和能效方面提供更好的性能[2],因为其不要求严格的线性,使得功率放大器的功效不会受调制方式的线性要求的严重影响,减少发送端的发送功率.因此,基于恒包络调制(比如MPSK)的SM技术必然拥有更大的优势[2].

本文基于调制符号固有的性质,并利用量化的原理,针对MPSK调制的SM系统,提出了两种复杂度与调制阶数无关的最优天线选择算法:EAQ-EDAS(Equal Amplitude and Quantization based EDAS)算法,利用MPSK各星座点符号具有相等的幅度的性质,简化了EDAS准则,然后利用2-D量化原理,求得所需的选择天线;RS-EDAS (Rotational Symmetry based EDAS)算法,利用调制符号本身的旋转对称性(RS),降低符号搜索空间的大小,进而降低算法的计算复杂度.两种算法在降低EDAS算法复杂度的同时实现了最优性能.

2　系统模型

y=Hx+n=hls+n

(1)

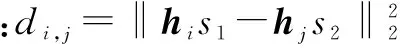
(2)

S表示调制符号集合,且|S|=M.那么,EDAS准则就是:计算各个天线组合中欧氏距离的最小值,然后寻找所有天线组合的最小值中的最大值,该最大值对应的天线组合,就是应当选用的天线组合,即:

(3)

3　低复杂度的最优天线选择算法

3.1EAQ-EDAS算法

EAQ-EDAS算法利用了MPSK星座图中各个星座点符号的幅度相等的特性.对于式(3)的EDAS准则,当i=j,s1≠s2时,可以表示为:

(4)

(5)

因为选择的天线的序号i,j和发送符号s1,s2是独立的,因此式(3)的内部优化问题可以分解为先求解发送符号,再求解天线序号的嵌套优化问题:

(6)

式(6)的求解可以分两步,先求解给定i和j条件下的s1和s2,然后再对i和j求解.下面我们讨论给定天线序号i,j的条件下,使得欧氏距离最小的s1,s2,即式(6)的内部优化问题,等价于:

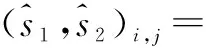
(7)

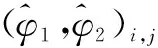
(8)

(9)

假设cosθi,j=a/c,sinθi,j=b/c,那么,根据三角函数积化和差公式,式(9)可以进一步化简得到:

(10)

根据余弦函数的性质,当φ2-φ1+θi,j=0即φ2-φ1=θi,j时,式(10)取值最大值,且最大值等于c.但φ2-φ1∈{2π*k/M},k∈{-M+1,…,M-1},θi,j∈[0, 2π]所以大部分情况下φ2-φ1不可能等于θi,j,只能求得满足条件且与θi,j最近的角度值.根据三角函数的性质,我们可以得到如下结论:

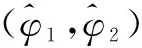
(11)

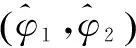
(12)

EAQ-EDAS算法总结如算法1

算法1EAQ-EDAS算法

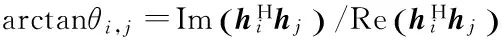
end

fork=1:N

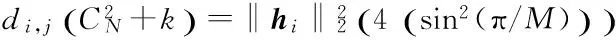
end

end

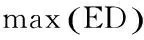
3.2RS-EDAS算法

RS-EDAS算法利用了旋转对称性,所以首先我们介绍旋转对称性的概念.

定义1(旋转对称性)假设复平面上有L个不同的点,等间隔的分布在同一个圆上,且圆心位于坐标原点,相邻两点之间的夹角为α(基本旋转角),则称这L个点彼此关于α旋转对称,这L个点构成的集合称为旋转对称集合.

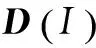
(13)

其中,Θ={1,2,…,N},Ii,Ij分别表示集合I中第i个和第j个元素对应的天线的索引.当i=j时,对于MPSK调制,可以求得|s1-s2|2的最小值为(2sin(π/M)2.当i≠j时,式(13)可以转换成实数矩阵表示:

D(I)i,j=

(14)

其中,Re(·)和Im(·)分别表示变量的实部和虚部.定义

(15)

(16)

此时式(14)可以表示为:

(17)

(18)

(19)

通过上面的推导我们可以知道,在EDAS算法求最优解过程中,只需对s2进行遍历即可,s1可以根据式(19)直接获得.那么如何简单快速搜索s2就成为降低EDAS算法复杂度的关键.本算法利用旋转对称性降低符号s2的搜索空间,进而降低EDAS算法的复杂度.为此,我们先给出下面的定理.

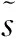
=u1coskα-u2sinkα

=u2coskα+u1sinkα

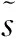
(20)

所以同一个旋转对称集中只需要搜索一个星座点即可.MPSK星座图中仅有1个旋转对称集,所以,MPSK调制下,符号搜索空间大小为1.根据上面的分析,RS-EDAS算法的搜索空间大小为nN2,其复杂度是全搜索EDAS算法复杂度的1/M2.

RS-EDAS算法总结见算法2

算法2RS-EDAS算法

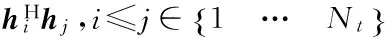
2:forl=1:n

根据(16)式求解R

令s2为MPSK星座图中任意一点,求解u1,u2,u

end

fork=1:N

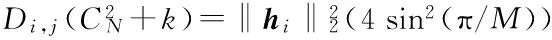
end

ED(l)=min(Di,j)

end

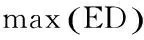
旋转对称性不仅是MPSK星座的性质,也是MQAM调制的特性,所以,基于旋转对称性的RS-EDAS算法一定可以用于MQAM调制的SM系统中.同样定理1也适用于MQAM调制,所以,MQAM调制的SM系统符号搜索空间为M/4个元素.

4　仿真结果与分析

本节在不同参数下的SM系统中对提出的算法和几种经典算法进行仿真,在所有仿真中我们都假设信道为瑞利衰落,噪声为加性高斯白噪声.

图2仿真的系统参数为Nt=6,Nr=4,N=4.仿真结果表明:(1)相同的系统中,天线选择技术可以降低系统的误码率,提高系统可靠性;(2)本文提出的两种算法都具有最优的性能;(3)文献[15]算法在MQAM调制下不是最优的,但在MPSK调制下是最优的.

图3仿真的系统参数为Nr=4,N=4SNR=10dB,8PSK调制.仿真结果表明随着Nt的增加,本文提出的算法仍然具有最优性能,同时相比于不进行天线选择的SM系统性能要好很多.

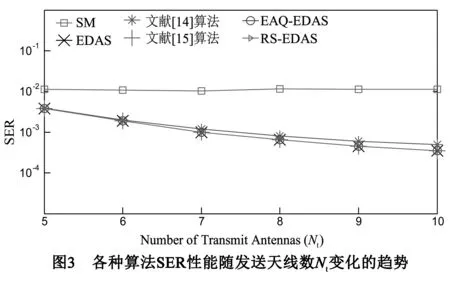
图4仿真的系统参数为Nt=6,N=4,SNR=10dB,8PSK调制.仿真结果表明随着接收天线数的增加算法的性能越来越好,这是因为接收分集增益变大了.

图5仿真的系统参数Nt=6,Nr=4,N=4,SNR=10dB,仿真点数为1000000.仿真时使用的是单核AMD Athlon 64 3500+处理器,核心速度1001.9MHz.仿真结果为了方便,采用了对数形式表示,结果表明全搜索DEAS算法复杂度与M2成正比;文献[14]的算法与全搜索EDAS算法相比有一定的降低;文献[15]的算法复杂度随M线性增加;本文提出的两种算法复杂度与M无关.

5　结论

在SM系统中,天线选择技术是提高系统的性能的有效途径.如何获得最优且低复杂度的天线选择方案是当前研究的一个热点问题.本文正是在这样的背景之下提出了两种低复杂度且最优的天线选择算法.两种算法充分利用了调制符号本身的性质,MPSK调制符号的等幅性和旋转对称性,结合2-D量化原理,降低天线选择算法的复杂度,同时不损失算法的性能.本文对提出算法的误符号率性能和复杂度进行了详细的分析和仿真,从理论和仿真两个方面证明了两种算法最优性.

目前,大天线技术和绿色通信技术正受到业界的广泛兴趣,使用恒包络调制信号(如MPSK)的SM 技术也受到关注,本文的提出的算法又对MPSK调制的SM系统有更强的优势,因此本文的算法有较好的实际应用意义.

[1]苏彦兵,谈振辉.基于天线选择的低秩信道MIMO系统容量研究[J].电子学报,2004,32(3):395-398.

SU Y B,TAN Z H.Capacity of deficient rank MIMO channels with antenna selection[J].Acta Electronica Sinica,2004,32(3):395-398.(in Chinese)

[2]RENZO DI M,HAAS H,GHRAYEB ALI.Spatial modulation for generalised MIMO:challenges,opportunities,and implementation[J].Proceedings of the IEEE,2014,102(1):56-103.

[3]RENZO DI M,HAAS H,GRANT P M.Spatial modulation for multiple-antenna wireless systems:a survey[J].IEEE Communications Magazine,2011,49(12):182-191.

[4]RENZO DI M,HAAS H.Bit error probability of spatial modulation(SM-MIMO) over generalised fading channels[J].IEEE Transactions on Vehicular Technology,2012,61(3):1124-1144.

[5]RENZO DI M,HAAS H.Transmit-diversity for spatial modulation(SM):Towards the design of high-rate spatially-modulated space time block codes[A].IEEE International Conference on Communications[C].Kyoto,Japan:IEEE,2011.1-6.

[6]BASAR E,et al.Space-time block coded spatial modulation[J].IEEE Transactions on Communications,2011,59(3):823-832.

[7]RENZO DI M,HAAS H.On transmit-diversity for spatial modulation MIMO:Impact of spatial-constellation diagram and shaping filters at the transmitter[J].IEEE Transactions on Vehicular Technology,2013,62(6):2507-2031.

[8]WANG J L,et al.Closed-loop spatial modulation with antenna selection[A].IEEE International Conference on Signal Processing[C].Beijing,China:IEEE,2012.1291-1294.

[9]CHUNG W Ho,HUNG C Y.Multi-antenna selection using space shift keying in MIMO systems[A].IEEE Vehicular Technology Conference[C].Yokohama,Japan:IEEE,2012.1-5.

[10]YANG P,et al.Adaptive spatial modulation for wireless MIMO transmission systems[J].IEEE Communications Letter,2011,15(6):602-604.

[11]张广驰,秦家银.放大转发MIMO中继系统中的快速天线选择算法[J].电子学报,2010,38 (1):68-73.

ZHANG G C,QIN J Y.Fast antenna selection algorithm in amplify and forward MIMO relay systems[J].Acta Electronica Sinica,2010,38 (1):68-73.(in Chinese)

[12]伍裕江,聂在平,乐铁军.基于极化可重构天线的天线选择方案[J].电子学报,2007,35 (12):2252-2257.WU Y J,NIE Z P,LE T J.Antenna selection scheme based on polarization reconfigurable antenna[J].Acta Electronica Sinica,2007,35 (12):2252-2257.(in Chinese)

[13]杨亮,秦家银.Nakagami-m Keyhole衰落信道下MIMO系统 容量及天线选择[J].电子学报,2006,34 (1):107-109.

YANG L,QIN J Y.Capacity and antenna Selection of MIMO system over keyhole nakagami-m fading channels[J].Acta Electronica Sinica,2006,34 (1):107-109.(in Chinese)

[14]NTONTIN K,et al.A low-complexity method for antenna selection in spatial modulation systems[J].IEEE Communications Letter,2013,17(12):2312-2315.

[15]ZHOU Q,et al.Reduced-complexity antenna selection schemes in spatial modulation[J].IEEE Communications Letter,2014,18(1):14-17.

[16]RAJASHEKAR R,HARI K V S,HANZO L.Antenna selection in spatial modulation systems[J].IEEE Communications Letter,2013,17(3):521-524.

[17]PILLAYN,XU H.Comments on ‘Antenna selection in spatial modulation systems’[J].IEEE Communications Letter,2013,17(9):1681-1683.

门宏志女,1988年6月出生于吉林,大连理工大学信息与通信工程学院博士研究生,主要研究方向无线通信MIMO技术研究.

E-mail:menruiye@sina.com

刘文龙男,1973年11月生于辽宁,现任大连理工大学信息与通信工程学院副教授,博士生导师,主要研究方向为MIMO及SM系统检测问题等.

E-mail:liuwl@dlut.edu.cn

王楠女,1989年11月生于吉林,2014年获得大连理工大学通信与信息系统硕士学位,主要研究方向为MIMO系统、空间调制系统检测算法研究.

E-mail:alisadlut@163.com

金明录男,1958年2月出生于吉林,先后在日本、韩国和澳大利亚等国家访问工作,现任大连理工大学信息与通信工程学院教授,博士生导师,主要研究方向为信号与通信系统基础理论与技术.

E-mail:mljin@dlut.edu.cn

Low-Complexity Antenna Selection Algorithms for Spatial Modulation Systems

MEN Hong-zhi,LIU Wen-long,WANG Nan,JIN Ming-lu

(TheSchoolofInformationandCommunications,DalianUniversityofTechnology,Dalian,Liaoning116023,China)

Spatial modulation (SM) is a special multi-antenna transmission technology,where the transmit antenna index is exploited to convey information except for modulation signals.In order to obtain transmit-diversity gains,antenna selection technology is introduced in SM systems to increase its demodulation performance.In antenna selection technology,Euclidean distance antenna selection (EDAS) is widely applied.However,its exhaust-search detection has extremely high complexity,which limits its application.Thus,exploiting the characteristics of modulation symbols and 2-D quantization,two low-complexity and optimal antenna selection algorithms are proposed.The simulation results show that the proposed algorithms reduce the computational complexity meanwhile achieving optimal performance.

spatial modulation (SM);antenna selection;low complexity.

2014-09-01;修回日期:2014-12-11;责任编辑:梅志强

国家自然科学基金(No.11372069);辽宁省自然科学基金(No.2013020033)

TN911.23

A

0372-2112 (2016)06-1322-06