一种基于奇异值谱加权的超声彩色多普勒成像杂波抑制算法

王录涛，吴　锡，金　钢，邹见效

(1.成都信息工程大学计算机学院，四川成都 610103； 2.中国空气动力研究与发展中心，四川绵阳 621000；3.电子科技大学自动化学院，四川成都 611731)



一种基于奇异值谱加权的超声彩色多普勒成像杂波抑制算法

王录涛1，吴锡1，金钢2，邹见效3

(1.成都信息工程大学计算机学院，四川成都 610103； 2.中国空气动力研究与发展中心，四川绵阳 621000；3.电子科技大学自动化学院，四川成都 611731)

针对超声彩色多普勒成像中由血管或血管周围组织时变运动引起的非平稳杂波抑制问题，提出一种基于奇异值谱加权的杂波抑制算法.首先根据单个慢时方向的回波多普勒矢量构建Hankel数据矩阵并进行奇异值分解，利用分解得到的Hankel主成分构造回归滤波器的正交基函数，同时引入改进的Sigmoid函数根据能量归一化奇异值谱计算回归滤波器系数，使得杂波区域的检测具有高度的特异性，从而提高非平稳杂波的抑制能力.为验证算法的有效性，利用商业级超声仪(Sonix RP,Ultrasonix Inc.)采集50帧人体颈动脉血流基带回波数据并进行滤波处理，滤波后数据采用滞一自相关法估计法计算血流平均速度与功率并进行成像.处理结果表明，与传统静态滤波器以及现有基于特征值分解的滤波算法相比，可有效增强组织空间高强度时变运动时血流与组织的区分能力.

超声彩色多普勒成像；非平稳杂波；Hankel奇异值分解；谱分析

1　引言

在超声彩色多普勒成像技术中，血管与血管周围慢动组织反射引起的杂波强度通常比血流信号强度高40～100dB，即使当采样容积位于血管中心位置处，由于采样容积的三维特性、合成声束旁瓣泄露、声波多重反射以及距离模糊等因素的影响，血流回波信号中也包含大量的杂波信号[1,2].杂波信号的存在导致血流动力学参数估计产生较大偏差，严重降低彩色血流成像系统的血流鉴别能力，因此杂波成分的充分抑制对于提高彩色超声多普勒系统成像质量有着至关重要的意义[3].

传统的杂波抑制滤波器，如有限冲击响应(Finite Impulse Response,FIR)滤波器、无限冲击响应(Infinite Impulse Response,IIR)滤波器、多项式回归滤波器等是一种静态滤波器，频域响应与输入数据无关[4].当杂波为平稳信号时，静态杂波滤波器可实现杂波的有效抑制，但对于由呼吸作用、血管搏动以及组织时变运动等引起的非平稳杂波，采用单一截止频率的静态滤波器实现血流动力学参数的准确估计则面临着巨大的挑战[5～7].

针对杂波信号的非平稳特性，Kruse等[8]提出了基于特征值分解(Eigen)的杂波滤波器设计方法.该方法利用回波多普勒信号协方差矩阵特征分解获得的特征矢量设计最优杂波滤波器，在已知杂波子空间维数的情况下，基于杂波基矢量构造回波滤波器使得杂波拟合均方误差最小，但Eigen 滤波器假设整个观察范围内的多普勒矢量信号是平稳的，不具有空间自适应性[9].Hankel-SVD滤波器根据单个慢时回波多普勒矢量构建Hankel数据矩阵并进行奇异值分解(Singular Value Decomposition,SVD)，利用高序Hankel主成分实现血流多普勒信号的重构，改善了杂波滤波器的空间自适应性[10～12].Eigen与Hankel-SVD滤波器均采用严格门限法根据预设阈值来确定回归滤波器系数，通过丢弃杂波成分与保留血流成分实现杂波抑制，在组织高强度时变运动时，难以取得一致的滤波效果[13,14].

本文提出一种基于奇异值谱加权的Hankel-SVD滤波方案(Hankel-SVD-WF)实现组织空间高强度时变运动导致的非平稳杂波的有效抑制.该方案根据单个慢时回波多普勒矢量构建Hankel数据矩阵并进行奇异值分解，但与常规Hankel-SVD仅采用高序Hankel主成分设计杂波抑制滤波器不同，利用改进的Sigmoid函数与能量归一化奇异值计算杂波滤波器系数，通过对各Hankel主成分赋予不同的权值实现血流多普勒信号的重构.最后采用人体颈动脉血流成像实例对杂波抑制性能进行量化对比.

2　Hankel-SVD

超声血流成像技术利用超声声束对成像区域进行扫描，在每一个扫描方向形成有限个发射声束，通过接收血红细胞散射的多普勒信号估计血流动力学参数[3].作为一种回归滤波器，Hankel-SVD滤波器根据Karhunen-Loeve变换将解调后的回波多普勒矢量信号表示为一组正交基矢量的线性叠加，通过保留与血流信号相对应的正交成分并进行信号重构，消除杂波对血流参数估计的影响[11].

对于包含N个采样值的单个慢时回波多普勒矢量x，其Hankel-SVD逼近可表示为：

(1)

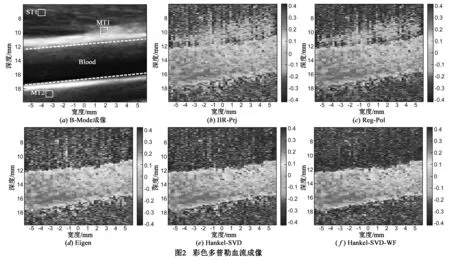
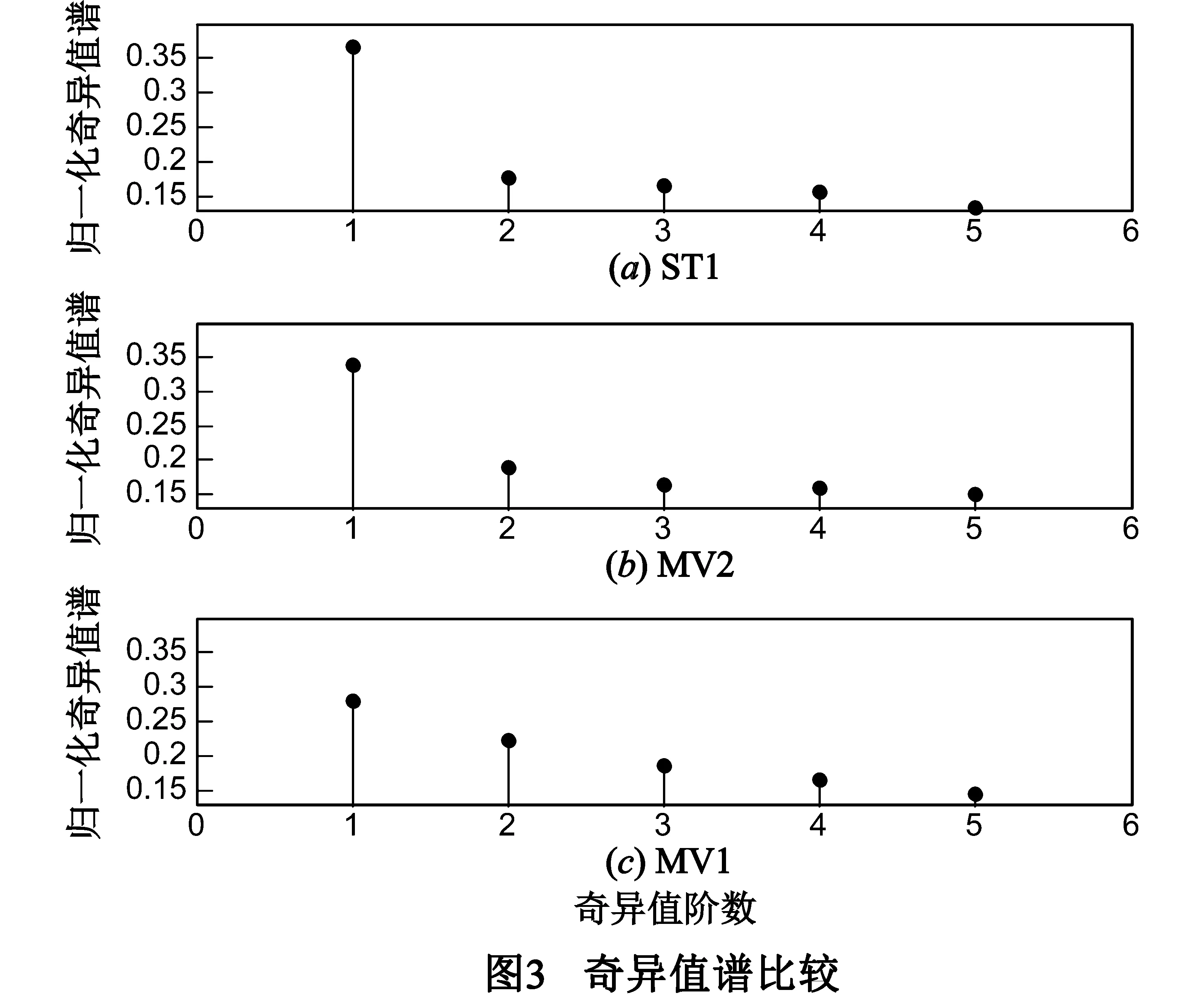
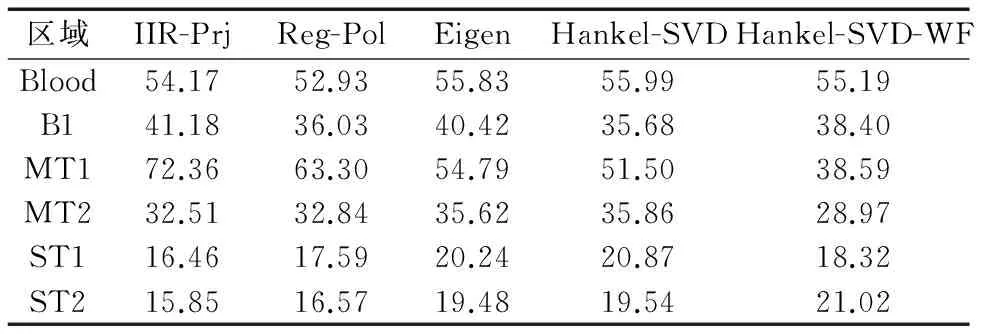
其中P(P

(2)

为计算式(1)中的正交成分，首先需将单个慢时多普勒矢量x分割成部分重叠的数据段并重新组织以构造Hankel矩阵：

(3)

其中,P满足P≤celi(N/2)，使得P≤N-P+1总成立.逐次采用单个慢时多普勒回波矢量构建Hankel矩阵并计算滤波器输出，不需要假设整个观察范围内的多普勒矢量信号是平稳的，因而具有空间自适应性.式(3)的SVD可表示为：

(4)

其中，Ak表示秩为1的第k阶Hankel成分，σk为奇异值，uk为N×1左奇异矢量，vk为(N-P+1)×1右奇异矢量.式(4)中的P个奇异值满足σ1>σ2>…>σP，因此Ak又可称为第k阶Hankel主成分.

分析Hankel矩阵的构造过程可知，在构造Hankel矩阵A时，输入信号矢量中的每个元素被沿反对角线方向重复配置，虽然经奇异值分解，Ak反对角线方向的元素不再相等，但仍可沿Ak反对角线方向对代表同一输入数据的所有元素求平均值来重建式(1)的正交基矢量γkφk，实现血流多普勒信号的准确重构.

3　奇异值谱加权Hankel-SVD滤波算法

3.1奇异值分解滤波系数及计算方法分析

将单个慢时回波多普勒矢量x沿Hankel-SVD基矢量φk分解后，奇异值滤波(Singular Value Filter，SVF)输出的一般化形式可表示为：

(5)

其中wk为滤波器系数，决定了滤波器的性能.与传统基于DFT的频域滤波技术不同，SVF无需信号频率构成的先验知识，根据观测信号不同成分的能量构成设计wk，并将其赋予反映输入信号各分量能量信息的基矢量φk实现期望信号的重构，因而可更加有效地将弱信号从强干扰信号中分离出来[10,11].

超声多普勒回波信号模型可表示为：

(6)

其中，s为血流信号，c为杂波，n为噪声.杂波由心壁、瓣膜、血管壁及静止的或慢速运动的肌肉产生的多普勒回波分量构成，平均频率较低但强度较高，在回波信号中占主导地位；血流信号由血红细胞散射的多普勒信号构成，强度较低，但频率成分高于杂波信号[1].

由超声多普勒回波信号模型可知，不同检测区域回波信号成分能量构成存在巨大差异，因此wk的取值应反映输入信号分量能量构成的统计特性，以避免杂波成分残留过多或降低血流信号成分被过多抑制的风险.目前，SVF系数自适应计算主要分为两类：基于奇异值门限值与基于Hankel主成分频率内容分析的方法[15,16].奇异值门限法根据预先设置的奇异值绝对值、奇异值差异或奇异值比率阈值，将回波信号成分分为杂波与血流两部分，由于组织空间分布差异与组织运动的时变性，回波信号不同成分的相对能量值出现较大差异，奇异值门限法很难保证滤波输出的一致性.Hankel主成分频率内容分析法采用滞一自相关法计算各阶Hankel主成分的平均频率，并与预设杂波频率、带宽比较以区分当前Hankel主成分所对应的信号分量的性质，但当杂波与血流频率非常接近或存在重叠时，仍无法避免低速血流信号丢失或高频杂波成分的泄漏.

3.2能量归一化奇异值谱

由奇异值分解原理可知，奇异值可充分表征输入信号不同成分能量集中情况.因此，本文将奇异值按照当前回波总能量进行归一化，并以此作为SVF系数计算的基础.能量归一化奇异值谱定义为：

(7)

其中，Σkk表示第k阶能量归一化奇异值.当回波信号源于静态组织区域时，杂波能量集中在第1阶奇异值上，其它归一化奇异值相对较小，当组织空间高强度时变运动时，杂波能量向高阶奇异值扩散，归一化能量谱趋于平坦，而当回波信号完全由噪声成分构成时，归一化能量谱最为平坦.由于输入信号的维数是大于奇异值谱噪声基底的奇异值的个数的函数[11]，因此能量归一化奇异值谱的分布特性可充分揭示回波信号的统计维数.与奇异值门限法和Hankle主成分频率内容分析法相比，采用Σkk计算SVF系数使得杂波区域的检测具有高度的特异性，进而增强针对由组织空间时变运动导致的非平稳杂波的抑制能力，同时使得低速血流信号得以有效保留.

3.3滤波器系数计算

根据超声多普勒回波信号模型与能量归一化奇异值谱，选取改进的Sigmoid函数计算SVF系数：

(8)

其中，α、τ为权函数参数.作为一种常见的S型函数，Sigmoid具有连续、光滑严格单调特性，能够较好平衡线性和非线性之间的行为，采用改进的Sigmoid计算滤波器系数能够更好的利用多普勒回波信号奇异值分布特性，增强滤波器杂波抑制性能的同时，尽可能保留低速血流信号.图1给出了τ=0.5，α取0、10、1000时SVF系数与能量归一化奇异值谱关系.

参数τ为杂波成分截止门限，取决于当前杂波分布特性.τ较小，则杂波成分难以得到充分抑制，平均血流速度估计出现较大负偏差，血流平均功率估计过高；τ较大则导致低速血流参数难以准确估计.α决定了Sigmoid函数的滚降特性，用以控制截止门限附近的基矢量的衰减程度，调整α可以有效改善杂波血流功率比，α较大有助于增强杂波抑制能力，但导致低速血流信号被抑制的风险增加.

在实际应用中，可根据最优的杂波血流功率比准则选择α，而τ则可由杂波Hankel主成分阶数k与能量归一化奇异值谱获得.当k已知时τ取值为：

(9)

4　颈动脉血流成像比较

为验证本文所提算法在临床诊断应用中的有效性，利用Sonix RP (Ultrasonix Inc.,Vancouver,Cannada)采集50帧人体颈动脉基带多普勒回波数据，每帧数据包含50条侧向扫描线，每线由轴向750个采样点构成，对每个采样点包含的多普勒回波矢量进行滤波处理，处理后的数据采用滞一自相关估计算法计算平均血流速度与功率并按空间扫描顺序排列以形成血流速度与功率分布图像.数据采集参数设置如表1所示.

表1　颈动脉血流成像数据采集参数设置

选取心脏收缩期一帧彩色超声多普勒回波数据比较5种不同滤波算法的性能，滤波器参数选择及门限值的设置应使得滤波后血流功率估计相近，以便于不同滤波器杂波抑制性能比较.图2给出了经滤波处理后、未设置速率门限与功率门限的血流成像结果.其中，IIR-Prj为2阶、归一化截止频率为0.1的投影初始化IIR滤波器，Reg-Pol为2阶Legendre多项式回归滤波器，Eigen滤波器的空间平滑长度为轴向15个采样点，杂波抑制-50dB；对于Hankel-SVD滤波器，构建Hankel矩阵时，P=5，采用频域阈值法确定杂波奇异值矢量阶数，设置杂波中心频率为100Hz，带宽为250Hz；Hankel-SVD-WF的滚降特性参数α=1000，杂波奇异值矢量阶数确定方法与Hankel-SVD相同.

图2(a)为B-Mode图像，在图中标出了颈动脉血管的空间位置，并根据相对血管壁距离标出了具有不同运动特性的组织区域，用以分析组织运动与奇异值谱分布的相关性，在其余图像中不同的颜色代表不同的速度估计结果.由于杂波成分主要由血管壁加速扩张以及连带的血管壁周围组织引起的多普勒回波分量构成，因此，可认为在远离血管区域组织受血管搏动影响较小，回波成分近似由静态杂波主导，因而可被充分抑制，滤波后残留噪声成分使得流速估计趋向于系统抗混叠速度，在图像中表现为红、蓝交错分布，而在靠近血管壁的绿色区域则表示受血管壁加速运动影响，杂波成分未能得以充分抑制，血流估计速度产生较大偏差.对比图2可知，图2(e)、(f)中杂波残留区域最小，图2(b)中最大，图2(d)优于图2(b)、(c)，这是因为Reg-Pol具有更加陡峭的过渡带，杂波抑制性能相对IIR-Prj有所改善，但在血管壁上边缘区域仍残留较多数量的杂波；Eigen滤波器根据回波多普勒信号统计特性，自适应选取杂波子空间维数，因而可显著改善非平稳杂波的抑制性能；Hankel-SVD根据慢时方向单个多普勒回波矢量的统计特性重构血流信号，具有空间平稳性，与Eigen滤波器相比，对血管空间高强度时变运动导致的非平稳杂波的抑制能力显著增强，而Hankel-SVD-WF则通过对血管边缘的准确检测，减少了血管左下方的血流溢出效应，有效提高了血流分布的可视化能力.

图3给出了图2(a) B-Mode图像中不同区域对应的能量归一化奇异值分布.ST1近似由静态组织构成，杂波能量集中在第1阶奇异值上，因而Σ11显著大于其它能量归一化奇异值；受血管壁的空时运动影响，MT1与MT2中杂波能量向高阶Hankel主成分扩散，Σ11减小，Σkk(k>1)增加，奇异值谱趋向平坦，杂波数据维数增加.因此，归一化奇异值谱分布能有效揭示组织运动特性，对杂波区域的检测具有高度的特异性.

图4为滤波后功率多普勒成像比较，滤波器参数设置同图2.从图4中可以看出，5种滤波器均可实现杂波成分的抑制，使得血流功率得以显现.在远离血管区域，杂波能量抑制最为充分；而在血管壁及其附近区域，血管的非匀速搏动使得杂波成分向高阶Hankel主成分扩展，滤波器的杂波抑制性能降低，导致在血管壁边缘残留了一定部分的较强杂波成分.比较血管附近区域的杂波功率可以发现，在血流功率近似相等的情况下，经Hankel-SVD-WF滤波处理后，杂波功率明显低于其它三种滤波算法，因此，杂波抑制能力最优.

为量化比较5种算法的杂波抑制性能，统计血流(Blood)、血流边缘(B1)、运动组织1(MT1)、运动组织2(MT2)、静态组织1(ST1)与静态组织2(ST2)6块不同区域滤波后平均功率并列入表2，各区域空间位置如图4(a) B-Mode图像中所示.分析表2中数据可知，相对于传统静态滤波器，自适应滤波器的杂波抑制性能显著提升.在MT1区域，相对Hankel-SVD与Eigen，Hankel-SVD-WF的杂波抑制度分别提高了约13.11dB与16.56dB，而在MT2区域，则分别提高了6.09dB与6.01dB.在B1区域，Hankel-SVD-WF功率比Hankel-SVD提高了约2.72dB，血管边缘的低速血流成分得以更好的保留.

表2　区域平均功率比较

5　结论

相比静态滤波器，自适应杂波抑制滤波器根据输入信号统计特性滤除杂波成分，可显著提高非平稳杂波的抑制性能.Hankel-SVD滤波器采用单个慢时方向的回波多普勒矢量构建Hankel数据矩阵，具有空间自适应性，相比Eigen滤波器空间非平稳杂波的抑制能力有所提升.在设计滤波器系数时，Hankel-SVD采用门限法，根据Hankel数据矩阵奇异值分解后获得的奇异值所表征的信号成分能量集中信息或各阶Hankel主成分反映的频域信息，通过与预设阈值比较，确定需保留的Hankel主成分.与Hankel-SVD硬门限准则不同，Hankel-SVD-WF根据多普勒回波信号模型与能量归一化奇异值谱所表征的组织运动信息，采用改进的Sigmoid函数，计算重构血流信号的回归滤波器系数.能量归一化奇异值谱的应用使得杂波区域的检测具有高度的特异性，而非二进制的滤波系数则可通过控制杂波截止成分附近的基矢量的衰减程度进一步获得最优的血流杂波功率比.颈动脉血流与功率成像结果表明，采用Hankel-SVD-WF，可显著改善组织空间高强度时变运动时的血流与组织的区分能力.

Sigmoid函数的参数α对于滤波后的血流杂波功率比有重要影响，探讨奇异值分布与最优α取值关系，进一步提高本文所提算法的性能是本课题下一步研究的内容.

[1]Oeltze S,Lehmann D J,Kuhn A.Blood flow clustering and applications in virtual stinting of intracranial aneurysms[J].IEEE Transactions on Visualization and Computer Graphics,2014,20(5):686-701.

[2]Shung K K.Diagnostic Ultrasound:Imaging and Blood Flow Measurements[M].New York:Taylor Francis Group,2006.34-37.

[3]Yap C H,Thiele K,Wei Q F.Novel method of measuring vascular regurgitation using three-dimensional nonlinear curve fitting of Doppler signals within the flow convergence zone[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2013,60(7):1295-1311.

[4]Kadi A,Loupas T.On the performance of regression and step-initialized IIR clutter filters for color Doppler systems in diagnostic medical ultrasound[J].IEEE Transactions on Ultrasonic,Ferroelectrics and Frequency Control.1995,42(3):927-937.

[5]Bjaerum S,Torp H,et al.Clutter filters design for ultrasound color flow imaging[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2002,49(2):693-704.

[6]Yoo Y M,Managuli R,Kim Y.Adaptive clutter filtering for ultrasound color flow imaging[J].Ultrasound in Medicine & Biology,2003,29(9):1311-1320.

[7]Yoo Y,Kim Y.New adaptive clutter rejection for ultrasound color Doppler imaging:In vivo study[J].Ultrasound in Medicine & Biology,2010,36(3):480-487.

[8]Kruse D E,Ferrara K W.A new high resolution color flow system using an eigen decomposition-based adaptive filter for clutter rejection[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2002,49(12):1384-1399.

[9]Yu A C H.Eigen-based signal processing methods for ultrasound color flow imaging[D].Toronto:Univ.of Toronto,2007.54-56.

[10]赵学智,叶邦彦.基于二分递推SVD的信号奇异性位置精确检测[J].电子学报,2012,40(1):53-59.ZHAO Xuezhi,YE Bangyan.Accurate detection of signal singularity position based on dichotomizing recursion SVD[J].Acta Electronica Sinica,2012,40(1):53-59.(in Chinese)

[11]朱凯然,何学辉,等.一种单自旋回波串信号参数估计方法[J].电子学报,2013,41(3):456-462.

ZHU Karan,HE Xuehui,et al.An aproach for parameter estimation of a single spin echo train signal[J].Acta Electronica Sinica,2013,41(3):456-462.(in Chinese)

[12]Yu A C H,Cobbold R S C.Single ensemble based eigen-processing methods for color flow imaging part 1 the Hankel-SVD filter[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2008,55(3):559-573.

[13]Song F,Zhang D,Gong X.Performance evaluation of eigendecomposition-based adaptive clutter filter for color flow imaging[J].Ultrasonics,2009,44(1):67-71.

[14]Yu A C H,Lovstaken L.Eigen-based clutter filter design for ultrasound color flow imaging:A review[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2010,57(5):1096-1011.

[15]Park G Y,Yeo S M,Yoon C H.HNew adaptive clutter rejection based on spectral decomposition and tissue acceleration for ultrasound color Doppler imagingH[A].IEEE International Ultrasonics Symposium H[C].Prague,Czech Republic:IEEE,2013.1484-1487.

[16]Yu A C H,Johnston K W,Cobbold R S C.Frequency based signal processing in Ultrasound color flow imaging[J].Canadian Acoustic,2007,35(2):11-23.

王录涛男，1979年3月出生，山东定陶人，博士后，成都信息工程大学讲师，从事医学成像、高性能嵌入式计算等方面有关研究.

E-mail:wltuestc@163.com

吴锡男，1980年3月生，四川成都人，博士，成都信息工程大学副教授，四川省学术和技术带头人后备人选，主要研究方向为数字图像处理、计算智能等.E-mail:wuxi@cuit.edu.cn

金钢男，1958年3月生，四川遂宁人，博士，中国空气动力研究中心研究员，博导，研究方向为信号工程、光学工程与流体力学.

E-mail:gjin@ioe.ac.cn

邹见效男，1978年12月生，江西吉安人，博士，电子科技大学教授、博导，研究方向为智能信息处理与控制、测控系统及信号处理技术与新能源控制技术.E-mail:jxzou@uestc.edu.cn

A Singular-Spectral-Weighting-Based Clutter Rejection Method for Color Ultrasound Doppler Imaging

WANG Lu-tao1,WU Xi1,JIN Gang2,ZOU Jian-xiao3

(1.DepartmentofComputeScienceandTechnology,ChengduUniversityofInformationTechnology,Chengdu,Sichuan610103,China;2.ChinaAerodynamicsResearch&DevelopmentCenter,Mianyang,Sichuan621000,China;3.SchoolofAutomationEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu,Sichuan611731,China)

Aiming at rejecting nonstationary clutter originating from slow moving vessels and surrounding tissues,a singular-spectral-weighting-based clutter suppression method for color ultrasound Doppler imaging is presented in this paper.First,a Hankel data matrix is created from each slow-time ensemble.Then,the singular value decomposition is performed to obtain the orthogonal basis functions for regression filtering.The coefficients of the filter are adaptively computed by a modified sigmoid function from the power normalized singular spectral,which allows for means to detect regions of clutter artifacts with high specificity.To analyze the efficacy of the proposed adaptive filter,in-vitro experiments were carried out.For the experiments,raw CFI data were acquired by a commercial ultrasound system (Sonix RP,Ultrasonix Inc.).Then,blood flow parameters are estimated from an estimate of the lag-one auto correlator of the filtered signal.The reconstructed flow and power images verifies that the proposed method outperforms other tested methods in rejecting high intense nonstationary clutter,which leads to improved distinguishing between blood and tissue regions.

ultrasound color Doppler imaging;nonstationary clutter;hankel singular value decomposition;spectral analysis

2014-07-17;修回日期:2015-07-16;责任编辑：梅志强

TN911.7

A

0372-2112 (2016)06-1294-06