以DNA为载体的线性时序逻辑模型检测
2016-08-12朱维军周清雷李永亮
朱维军,周清雷,李永亮
(郑州大学信息工程学院,河南郑州 450001)
以DNA为载体的线性时序逻辑模型检测
朱维军,周清雷,李永亮
(郑州大学信息工程学院,河南郑州 450001)
线性时序逻辑模型检测被广泛应用于处理器设计与验证、网络协议验证、安全协议验证等领域.然而到目前为止,该技术只能在电子计算的平台上实现.为了以脱氧核糖核酸(Deoxyribo Nucleic Acid,DNA)为载体对线性时序逻辑(Linear Temporal Logic,LTL)实施模型检测,给出了使用粘贴自动机实现Until算子模型检测的方法.首先,使用粘贴自动机对Until公式的有穷状态自动机(Finite State Automata,FSA)模型进行编码;然后,将系统模型转换为粘贴自动机的输入字符串;最后,用粘贴自动机验证系统是否满足公式.仿真实验结果证实,新方法可实现对LTL逻辑时序算子的检测.
模型检测;脱氧核糖核酸;线性时序逻辑;粘贴自动机
1 引言
模型检测由图灵奖得主Clarke教授等人提出[1].它是一种能够自动验证系统是否满足给定性质的形式化核心方法与技术,被广泛地应用于硬件验证[2]、网络协议验证、安全协议验证[3]等领域.在时序逻辑模型检测中,线性时序逻辑[4](Linear Temporal Logic,LTL)、计算树逻辑[5](Computation Tree Logic,CTL)分别被用来描述系统需满足的线性时序性质和分支时序性质,有穷状态自动机(Finite State Automata,FSA)则被用来为系统建模,模型检测算法自动检测模型是否满足需求性质.
脱氧核糖核酸(Deoxyribo Nucleic Acid,DNA)计算以DNA分子为载体,以生物酶和生物操作作为信息处理工具,是一种与电子计算不同的计算模型.1994年,图灵奖得主Adleman教授发表在《Science》上的一篇文章用DNA实验求解了一个小规模的哈密顿路径问题[6],被认为是DNA计算领域的开创性工作.由于DNA分子在实验操作上相对容易,分子机构上便于信息处理,DNA计算得到快速发展.学者们提出了诸如过滤模型[7]、粘贴自动机[8]等等DNA计算模型,并用这些模型成功解决了一系列NP难题:中国邮递员问题和0-1规划问题的DNA算法[9,10]、图的最大团问题和最小覆盖问题的DNA算法[11,12]、图着色问题的DNA算法[13].特别是,许进教授等人用并行DNA计算模型解决了61个顶点的3着色问题[14].最新的一系列研究[15~17]更是涉及到了纳米器件与DNA自组装.
在经典计算中的模型检测,状态空间与效率始终是困扰研究人员的难题.DNA计算具有强大的并行处理能力,可为模型检测效率提升提供新的思路.2006年,图灵奖得主Emerson教授提出了一种用DNA分子进行CTL模型检测的思路与构想,给出了CTL公式EFp的DNA模型检测方法[18].这是使用DNA计算实现模型检测的一个尝试.然而,该方法不能对一般CTL公式实施检测,更不能对LTL公式进行检测.为此,我们研究以DNA分子为载体的LTL模型检测方法.
2 线性时序逻辑与FSA
2.1线性时序逻辑
LTL逻辑的一阶部分不可判定,因此我们只需研究其命题部分(Propositional LTL,PLTL).
定义1设AP是原子命题集合,如果φ和ψ是PLTL公式,那么,p∈AP、┑φ、φ∨ψ、φ▷ψ都是PLTL公式.
定义2一个PLTL模型是一个三元组M=(S,R,L),其中:
(1)S是非空有穷状态集,s∈S是状态;
(2)R:S→S,R(s)是状态s的唯一后继状态;
(3)L:S→2AP,L(s)是在状态s中成立的原子命题的集合.
定义3满足关系╞定义如下:
(1)s|=p当且仅当p∈L(s);
(2)s|=┑φ当且仅当┑(s|=φ);
(3)s|=φ∨ψ当且仅当(s|=φ)∨(s|=ψ);
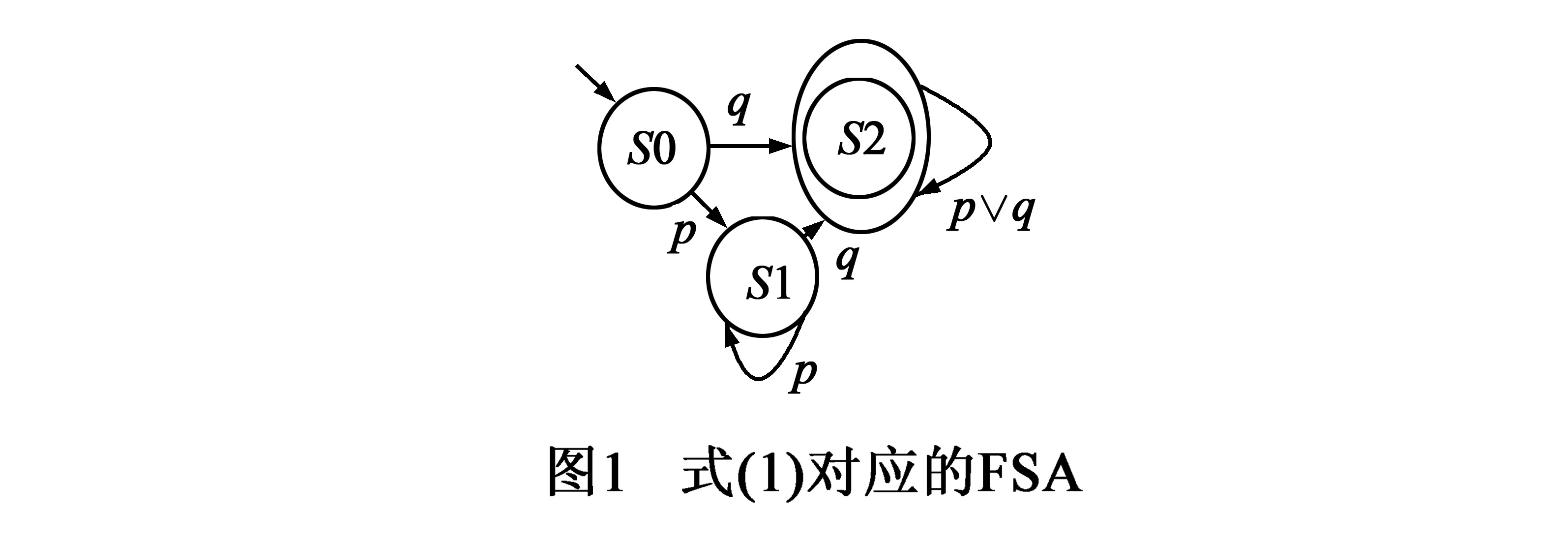
(4)s|=φ▷ψ当且仅当 ∃j≥0.Rj(s)|=ψ∧(∀0≤k 2.2FSA 定义4一个FSAA是一个五元组(Σ,Q,T,q0,F),其中: (1)Σ是一个有穷非空字母表; (2)Q是一个有穷非空状态集; (3) 转移函数T:Q×Σ→R(Q); (4)q0∈Q是起始状态; (5)F⊆Q是接受状态集. 定义5设w=y1,…,ym是定义在Σ上的字符串,如果存在Q中状态序列r0,r1,…,rm满足: (1)r0=q0 (2)ri+1∈T(ri,yi+1),i=0,1,…,m-1 (3)rm∈F 则称w是被A接受的文字. 定义6A识别的语言是被A接受的文字的集合. 粘贴自动机[8]是一种实现FSA的DNA计算模型,给定输入字符串的DNA链,粘贴自动机模型能够判断字符串是否被自动机接受. 3.1FSA和输入字符串的编码方式 假设M=(Σ,S,T,s0,F)是一个FSA,字母表Σ中的任意一个字符a都可以用单链DNA编码为C(a). (1)Σ上的输入字符串w=a1,…,an用一个DNA单链编码:5′I1X0…XmC(a1)…X0…XmC(an)X0…XmI23′,其中,I1是启动区序列,X0…Xm是间隔序列,用来间隔字符ai的编码C(ai),I2是终止区序列. 3.2计算过程 粘贴自动机模型的计算过程分为3步: 第一步:数据预处理 (1) 合成输入字符串和自动机的编码链. (2) 将所有的DNA链放到试管T中,使互补链充分结合. (3) 在试管中T加入DNA连接酶,得到(部分)双链DNA分子. 第二步:计算 经过第一步的数据处理,如果输入字符串被自动机接受,那么试管T中应该是以启动区开始以终止区结束的完全双链的DNA分子;否则,试管T中的DNA不是完全双链,要么终止区是部分双链,要么启动区和终止区中的某部分是部分双链的.根据上述情况,可以向试管T中加入Mung Bean核酶,降解其中的单链DNA片段,保留完全双链的DNA分子. 第三步:输出结果 向试管T中加入Mung Bean核酶后,可以利用电泳技术分离不同长度的DNA分子,如果存在两种或者两种以上的不同的DNA分子质量,说明在加入核酶前,试管T中存在部分双链的DNA分子,输入字符串不被自动机接受;否则,在加入核酶前,T中全部是完全双链DNA分子,输入字符串是被自动机接受的. 4.1将PLTL公式转换为FSA PLTL的基本核心公式如下: p▷q (1) 图1是式(1)的FSA模型.按照粘贴自动机模型中FSA的编码方式编码图1中的自动机,将编码好的DNA单链放到试管R中. 4.2生成系统模型的符合粘贴自动机的输入字符串格式的运行 首先,我们用图2所示的单链DNA对系统的状态进行编码.其中:X0…Xm是粘贴自动机中的间隔序列,为满足粘贴自动机输入字符串的格式而增加;L(s)是状态标签函数;Y用来调节编码,使每个状态编码的长度为相等的偶数,并且保证状态和状态编码之间一一对应. 在状态编码的基础上,我们可以使用算法1生成系统自动机模型中以开始状态为始点以终止状态为终点的所有路径.算法描述如下. 算法1系统模型自动机的运行路径生成算法 Input:公式(1)的自动机模型M Output:表达M所有路径的所有DNA分子 BEGIN 第1步:对于每个状态s,向试管T中加入s的编码;对于每条边e,向试管T中加入e的编码.经过退火和连接反应,生成系统的FSA模型中的随机路径. 第2步:对试管T执行提取前缀操作,使试管T中只含有以开始状态为起点的路径. 第3步:对试管T执行提取后缀操作,使试管T中只含有以终止状态为终点的路径. 第5步:通过亲和纯化技术,过滤出试管T中所有包含I1和I2序列的单链DNA分子. END 其中,第5步除去第4步中多余的DNA分子,得到满足粘贴自动机输入字符串格式要求的单链DNA分子,每条单链DNA对应系统的一个运行. 4.3用粘贴自动机验证系统是否满足PLTL公式 4.1节获得表征式(1)模型的单链DNA分子;4.2节的算法则得到了表征系统模型的单链DNA分子.在此基础上,我们通过让上述两类单链DNA分子充分地进行生化反应,即可检测系统是否满足式(1).检测方法如算法2所示.需要补充说明的是,我们可以证明:要验证一个系统是否满足式(1),只需验证系统的长度小于|V|*2|V|-1+|E|的所有运行是否满足式(1).篇幅所限,不再给出详细证明过程. 算法2公式(1)的DNA模型检测算法 Input:4.1节的试管R,即式(1)对应的粘贴自动机的编码;算法1获得的试管T,即系统的所有运行 Output:系统模型是否满足公式 BEGIN 第1步:用长度分离操作提出试管T中长度小于|V|*2|V|-1+|E|的单链DNA. 第2步:合并试管R到T,在T中加入DNA连接酶,使互补链充分反应. 第3步:充分反应后,在试管T中加入MungBean核酶,降解所有单链DNA. 第4步:对T执行分离操作,得到试管T1和T2,T1中是含有启动区的DNA链,T2中则是不含的. 第5步:检测T2.若T2中有DNA链,则它不含启动区,它是第2步中的部分双链DNA分子被第3步中的核酶切开后的产物,第2步含有部分双链DNA分子,系统有不满足式(1)的运行.否则,执行下一步. 第6步:对T1执行分离操作,得到试管R1和R2,R1中是含有终止区的DNA链,R2中则是不含的. 第7步:检测R2,如果R2中有DNA链,那么它只含有启动区而不含有终止区,它是第2步中的部分双链DNA分子被第3步中的MungBean核酶切开后的产物.第2步含有部分双链DNA分子,说明系统有不满足式(1)的运行.否则,系统的所有运行都被粘贴自动机接受,系统满足式(1). END 式(1)对应的自动机接受的运行会产生完全双链DNA分子,它既含有启动区又含有终止区,不会被MungBean核酶切开;而不被自动机接受的运行会产生部分双链DNA分子,将被MungBean核酶切开,切后的产物要么只含有启动区,要么只含有终止区.算法2就是根据这个事实检测的. 4.4复杂度分析 算法2有两个输入:系统模型的符合粘贴自动机输入字符串格式的运行;式(1)对应的粘贴自动机模型. 假设系统模型有x个状态、y条边,算法1生成系统模型的符合粘贴自动机输入字符串格式的运行.第1步要合成所有状态和边的编码,此步共需执行x+y个操作步骤;第2、3、5步,每步均需执行1个操作步骤;第4步需执行2个操作步骤,(分别为加入两个DNA分子).因此,生成系统模型的符合粘贴自动机输入字符串格式的运行的时间复杂度是O(x+y)+O(3)+O(2)=O(x+y). 假设有限状态自动机M有m个状态、n条边,在建立其对应的粘贴自动机模型的过程中,合成所有状态和边的编码共需m+n个操作步骤,而式(1)对应的自动机中,m=3、n=6,因此,建立式(1)对应的粘贴自动机模型共需执行9个操作步骤. 最后,在用粘贴自动机模型验证系统运行是否满足式(1)的算法2中,这7步中的每一步都需要执行1个操作步骤.综上所述,算法2的时间复杂度是O(x+y)+O(9)+O(7)=O(x+y). 表1给出了新算法与相关方法的复杂度比较. 表1 时序逻辑模型检测的DNA方法的检测效率之比较 我们在Win7操作系统上,用VB语言编写实验程序以实现算法.新方法涉及的所有分子生物元操作,均已在现有的DNA计算相关工作中被使用,这些元操作的有效性也已被前人工作中的真实分子生物实验所证实.因此,本文采用仿真实验代替真实生物实验,获得的结果是可信的. 表2和表3给出了实验的编码方式.在此基础上,我们实施了两个仿真实验. 表2 输入字符串的编码规则(即系统的运行,按照粘贴自动机输入字符串的编码方式编码) 表3 式(1)对应的自动机(按照粘贴自动机的编码方式编码) 实验1系统模型如图3,|V|=3,|E|=3,要验证的系统运行的最大长度是15.由图3可知:在状态0,p和q同时满足;由表2最后一行可知,p对应的编码是GG,q对应的编码是TT;因此状态0对应的编码是GG/TT,其中斜线表示“或”,即不同的DNA分子可在p和q任选其一.依次类推,状态1对应的编码是GG,状态2对应的编码是TT.表4是系统模型长度不超过15的所有7个运行.算法2让表3中单链DNA分子与表4中的单链DNA分子进行充分的生化反应,得到的双链DNA分子如表5所示,即为系统运行7条路径的检测结果.由表5可见,所有路径都是完整的双链DNA分子,这表明所有运行均满足p▷q,因此系统满足p▷q. 表4 实验1的系统运行 路径路径的DNA编码或者路径经过的顶点顺序1号路径的编码ATATCAAGCTACGG/TTCAAGCTACGGCAAGCTACTTCAAGCTACCGCG1号路径的顶点顺序0,1,22号路径的编码ATATCAAGCTAC(GG/TTCAAGCTACGGCAAGCTAC)2TTCAAGCTACCGCG2号路径的顶点顺序0,1,0,1,2k号路径的编码ATATCAAGCTAC(GG/TTCAAGCTACGGCAAGCTAC)kTTCAAGCTACCGCGk号路径的顶点顺序(0,1)k,27号路径的编码ATATCAAGCTAC(GG/TTCAAGCTACGGCAAGCTAC)7TTCAAGCTACCGCG7号路径的顶点顺序0,1,0,1,0,1,0,1,0,1,0,1,0,1,2 表5 实验1的系统运行的检测结果 实验2系统模型如图4,|V|=3,|E|=4,要验证的系统运行的最大长度是16.由图4可知:状态0对应的编码是GG/TT,状态1对应的编码是GT,状态2对应的编码是TT.表6是系统模型长度不超过16的所有29个运行.算法2让表3中的单链DNA分子与表6中的单链DNA分子进行充分的生化反应,得到的双链DNA分子如表7所示,即为系统运行29条路径的检测结果. 由表7可见,存在一部分路径不是完全的双链DNA分子,说明这些路径不满足p▷q.因此系统不满足p▷q. 表6 实验2的系统运行 表7 实验2的系统运行的检测结果 续表 实验1和实验2分别针对系统满足公式和系统不满足公式这两种情况进行仿真检测.把有关这些实验所获结果的表格(表4、表5、表6和表7)综合起来,我们可以看出:无论系统模型是否满足式(1),该式都可以使用DNA分子来实现模型检测;特别是,当系统不满足式(1)时,新算法可以给出反例,以具体指出是系统中的哪些路径不满足公式,正如表7中的单号路径所示. 进一步地,我们把有关新方法的上述实验结果与相关方法进行比较,结果如表8所示.从表中不难看出:文献[18]给出的是针对CTL公式的DNA模型检测方法;而本文给出的是针对LTL公式的DNA模型检测方法.由于Until是LTL公式的核心算子,Final与Always等其它时序算子表达的公式均可转化为Until算子表达的公式,因此,时序算子加原子命题组成的LTL公式就可以在DNA分子上实施模型检测.这是新算法相对于文献[18]中方法的比较优势. 表8 时序逻辑模型检测的DNA方法的检测能力之比较 本文的主要成果是算法2.使用该算法即可在DNA计算框架内实现LTL逻辑的核心算子模型检测.这是本文工作的贡献.一方面,基于DNA计算的方法可利用其巨大的天然的并行计算优势缓解LTL模型检测当前面临的状态空间爆炸这一瓶颈,这是新算法在计算机科学中的潜在应用价值.另一方面,在细胞内进行的LTL模型检测计算,将使得对肿瘤分子标志发展过程的动态识别与动态地自动调整药物用法与用量成为可能,进而有望为人类疾病的分子诊疗提供更好的自治智能方法,这是新方法在分子生物学与医学中的潜在应用价值. [1]CLARKE E.Model Checking[M].Massachusetts:MIT Press,1999. [2]BAMAT J,BAUCH P,BRIM L,et al.Designing fast LTL model checking algorithms for many-core GPUs[J].Journal of Parallel and Distributed Computing,2012,72(9):1083-1097. [3]CARBONE R.LTL model-checking for security protocols[J].AI Communications,2011,24(3):281-283. [4]GOTZHEIN R.Temporal logic and applications-a tutorial[J].Computer Networks and ISDN Systems,1992,24(3):203-218. [5]BENARI M,PNUELI A,MANNA Z.The temporal logic of branching time[J].Acta Informatica,1983,20(3):207-226. [6]ADLEMAN L.Molecular computation of solutions to combinatorial problems[J].Science,1994,266(5187):1021-1023. [7]ADLEMAN L.On constructing a molecular computer[J].Discrete Mathematics and Theoretical Computer Science,1995,27:1-21. [8]ZIMMERMANN K,IGNATOVA Z,PEREZ M.DNA Computing Models[M].Berlin:Springer,2008. [9]YIN Z X,ZHANG F Y,XU J.A Chinese postman problem based on DNA computing[J].Journal of Chemical Information and Computer Sciences,2002,2(42):222-224. [10]YIN Z X,ZHANG F Y,XU J.The general form of 0-1 programming problem based on DNA computing[J].Biosystems,2003,70(1):73-79. [11]PAN L Q,XU J,LIU Y C.A surface-based DNA algorithm for the maximal clique problem[J].Chinese Journal of Electronics,2002,11(4):469-471. [12]PAN L Q,XU J.A surface-based DNA algorithm for the minimal vertex cover problem[J].Progress in Natural Science,2003,13(1):81-84. [13]高琳,许进.图的顶点着色问题的DNA算法[J].电子学报,2003,31(4):494-497. GAO Lin,XU Jin.A DNA algorithm for graph vertex coloring problem[J].Acta Electronica Sinica,2003,31(4):494-497.(in Chinese) [14]XU J,QIANG X L,ZHANG K,et al.A parallel type of DNA computing model for graph vertex coloring problem[A].2010 IEEE Fifth International Conference on Bio-inspired Computing:Theories and Applications[C].Changsha:IEEE Press,2010.231-235. [15]YANG J,DONG C,DONG Y,et al.Logic Nanoparticle beacon triggered by the binding induced effect of multiple inputs[J].ACS Applied Material Interfaces,2014,6(16):14486-14492. [16]ZHANG C,WU L,YANG J,et al.A molecular logical switch beacon controlled by thiolated DNA signals[J].Chemical Communications,2013,49:11308-11310. [17]ZHANG C,MA J,YANG J.Nanoparticle aggregation logic computing controlled by DNA branch migration[J].Applied Physics Letters,2013,103(9):093-106. [18]EMERSON E A,HAGER K D,KONIECZKA J H.Molecular model checking[J].International Journal of Foundations of Computer Science,2006,17(04):733-741. 朱维军男,1976年生于河南郑州,现为郑州大学副教授.主要研究方向:DNA计算、形式化方法. E-mail:zhuweijun76@163.com 周清雷男,1962年生于河南新乡,现为郑州大学教授、博士生导师.主要研究方向:DNA计算、形式化方法. E-mail:ieqlzhou@zzu.edu.cn Conduct Linear Temporal Logic Model Checking via DNA Molecules ZHU Wei-jun,ZHOU Qing-lei,LI Yong-liang (SchoolofInformationEngineering,ZhengzhouUniversity,Zhengzhou,Henan450001,China) The linear temporal logic (LTL) model checking is widely used in processor design and verification,network protocol verification and security protocol verification.Up to now,this technique can only be realized on the platform of electronic computer.In order to conduct LTL model checking under the circumstance of deoxyribo nucleic acid (DNA),we proposed a method to check the Until constructor via a sticker automaton.We encode a finite state automaton (FSA) which is a model of the formula Until,with a DNA sticker automaton.And we convert a model of a system into its paths,as the input strings of the sticker automaton.We verify whether the system satisfies the formula or not,by using the sticker automaton.In this way,the formula Until can be checked with the double strand DNA molecules.The simulation results show that the method can successfully check the basic temporal formulas. model checking;deoxyribo nucleic acid;linear temporal logic;sticker automaton 2014-11-15;修回日期:2015-01-27;责任编辑:覃怀银 国家自然科学基金(No.61250007,No.U1204608,No.U1304606,No.61572444);中国博士后科学基金(No.2012M511588,No.2015M572120);河南省高等学校青年骨干教师资助计划项目(No.2014GGJS-001) TP301;TP384 A 0372-2112 (2016)06-1265-073 粘贴自动机

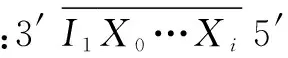
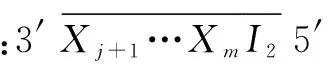
4 用粘贴自动机实现PLTL模型检测

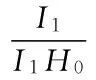

5 仿真实验










6 结论


