概念生成 无中生有——“数轴”教学设计

季　军（新疆生产建设兵团第二中学）



概念生成无中生有
——“数轴”教学设计

季军（新疆生产建设兵团第二中学）

摘要：概念是人对能代表某种事物或发展过程的特点及意义所形成的思维结论.实现概念生成教学的关键在于组织课堂教学时如何设计“生成”这一环节，教师以问题驱动，在“步步为营”的预设中，让学生逐渐“走近”，并最终“走进”概念的本质，还原概念的形成过程.下面以数轴为例谈谈本人的做法.

关键词：概念生成；教学设计；数轴

教材分析

“数轴”是人教版《义务教育教科书·数学》七年级上册第一章第二节的内容，其主要内容是数轴的概念及简单的应用.它是在学习了正、负数和有理数之后的重要内容，也是学生第一次接触数形结合的实例.数轴是学习后面知识的重要工具.例如，相反数、绝对值、有理数运算法则和一元一次不等式及不等式组中都会应用到，还是今后学习平面直角坐标系的基础.

学情分析

学生学习数轴的难点在于概念的形成过程中三要素的建立，及概念的准确和深入理解.因此，教学中要让学生经历概念的三要素的生成过程，从而初步体会数形结合思想.

教学目标

（1）建立数轴的概念，能用数轴上的点表示有理数，能够在数轴上发现相关的数学规律.

（2）经历数轴概念的形成过程，初步体会数形结合和分类讨论的数学思想.

（3）培养学生用新的数学语言对原有的数学现象加以概括的能力.

（4）培养学生善于发现规律的能力，体验获得成功的乐趣.

教学重、难点

重点：建立数轴的概念，能将有理数在数轴上表示出来.

难点：理解数轴概念的形成过程，正确画出数轴，发现有理数在数轴上有序的排列，以及相关规律.

教学过程设计

1.创设情境，引入新课

问题情境：

在一条东西向的马路上，有一个汽车站牌，汽车站牌东3米和7.5米处分别有一棵柳树和杨树，汽车站牌西3米和4.8米处分别有一棵槐树和一根电线杆，试画图表示这一情境.

师生活动：教师利用多媒体呈现文字材料，集中所有学生的注意力.学生读题并思考.

【设计意图】多媒体呈现材料，学生读题并思考问题，体现注意的指向性和集中性.教师引领学生快速进入角色.

2.提出问题，探究新知

问题1：题目中描述的情境可以画图表示吗？如果要画出来我们可以用什么图形当作一条东西向的马路？

师生活动：学生动手尝试画出图形.教师给予指导，并让学生相互比较画出的图形.学生容易发现自己与其他学生所画的图形不完全相同.

教师追问：我们描述的是同一个情境，为什么画出的图形会不一样呢？

师生活动：学生思考教师提出的问题，注意到周围的其他学生所描绘的柳树的位置有的离站牌近一点，有的离站牌远一点.

教师引导学生关注比例尺（单位1）不统一问题，引导出数轴概念的要素——单位长度.

教师追问：在直线上，你先标出的是汽车站牌，还是柳树、杨树，或者是电线杆？为什么？同学们将汽车站牌都标在了中间的位置，为什么没有标在左边或者右边？

师生活动：学生思考教师提出的问题，逐渐明白汽车站牌是这个问题中的基准（原点）.教师引导学生思考，并理解汽车站牌是这个问题中的基准（原点）这一要素.

教师追问：有位同学说距离汽车站牌3米处是柳树，另一位同学说不对，距离汽车站牌3米处是槐树.这两位同学出现了认知上的矛盾，他们都有道理吗？能用我们所学的知识解决这个问题吗？

师生活动：教师引导学生思考问题并加以解决，从而形成正方向这一要素.在教师的引导下，学生利用曾经学过的知识具有相反的意义解决问题生成正方向，在图形中标注，并将槐树的3米处改成-3，电线杆的4.8米处改成-4.8.

【设计意图】通过恰当设疑，引发学生的思考，唤醒学生已有的知识储备，归纳出共同的特点，即比例尺（单位1），基准，具有相反的意义.

师生活动：教师根据学生的回答，逐步分析并依次板书共同特点，形成数轴概念，具体过程如下：

比例尺（单位1）→ 单位长度

基准→原点

具有相反的意义 → 正方向

在我们今后要学习的内容中，比例尺（单位1）我们称作单位长度，用1标示.基准在数学中我们称作原点，用0标示.具有相反的意义要求我们做出规定，通常来讲原点向右为正方向，在图形中用箭头表示.

在数学中，规定了原点、正方向和单位长度的直线叫做数轴.

【设计意图】用规范的数学语言对上述共同特点加以概括，即单位长度、原点和正方向.从而形成数轴的概念.

问题2：生活中有什么物体与数轴相似？什么地方让我们感受到很相似？

师生活动：教师提出问题来引导学生与生活实物联系.学生思考联想到直尺、温度计.说出相似的地方：有原点，有1刻度（单位长度），零上温度的方向是正方向.

教师追问：那我们可不可以认为温度计是数轴？

师生活动：教师提出问题，引导学生思考温度计与数轴的区别.有的学生说可以认为温度计是数轴，并能够说出相同的地方；还有学生持相反的观点，原因是直尺、温度计都是线段，数轴是直线.

【设计意图】学生通过数轴与生活中的实例的联系、对比、辨析，达到进一步清晰数轴概念的目的.

问题3：请同学们仔细观察，图1的这四幅图中哪一幅是数轴，其他的为什么不是数轴？

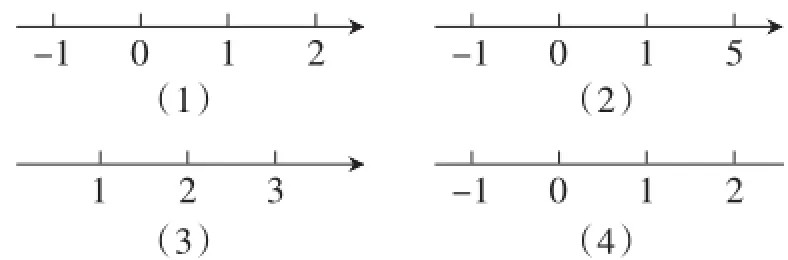
图1

师生活动：教师引导学生根据刚学的数轴的知识得出答案.学生回答紧扣数轴的定义，并说出其他图形不是数轴的原因.说不完整的可以由其他学生补充.

3.理解新知，巩固新知

问题：说出如图2所示的数轴上A，B，C，D各点表示的数.

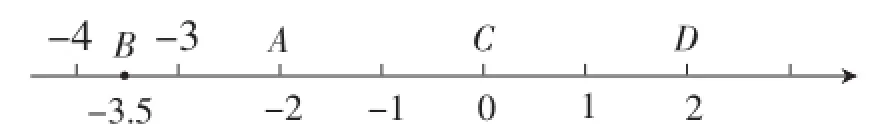
图2

师生活动：教师引导学生正确读出各点所表示的有理数.学生根据所学知识读出各点所表示的有理数，如果有误，则请其他学生加以更正.

教师追问：图2有什么地方看着不美观、不舒服呢？

师生活动：教师引导学生发现-3，-4应该统一写在数轴下方.学生在教师的引导下理解数轴的规范性和美观感受.

【设计意图】学生读出数轴上的点表示的有理数是对数轴概念的正确理解，也是数与形的完美结合.

4．探索发现，总结规律

问题：我们学习了数轴，请你画出一条数轴，并在数轴上表示下列有理数.

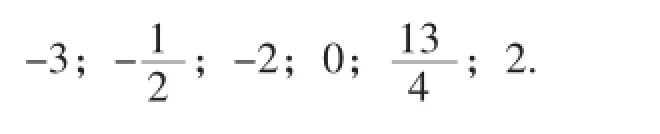
师生活动：请一位同学上黑板表示.教师观察并指导学生在数轴上正确表示有理数.提出问题引导学生得出数轴上还可以表示更多有理数.学生思考并回答问题，通过与更多的学生互动，在数轴上表示更多的有理数.

教师追问：老师想表示一个有理数1000，能在这个数轴上表示出来吗？

师生活动：根据学生的回答引导学生得出正确的解释.学生在教师引导下得出数轴是直线，可以无限延伸，又或者改变单位长度1所表示的长度，从而解决问题.

【设计意图】通过问题驱动，及时从学生的回答中获取反馈信息，完善数轴上所需要的信息点，为下面学生观察、发现、获得相关数学规律做好铺垫.

教师追问：那所有的有理数能不能都在数轴上表示出来？

师生活动：根据同学们的回答引导学生得出正确的猜想后，板书结论.学生根据上面的活动和教师的引导得出结论，即所有的有理数都能在数轴上表示.

教师追问：这条数轴上表示了很多正数、负数，你能发现这些数在数轴上的位置有什么特点吗？

师生活动：教师引导学生发现规律并板书.学生通过观察和教师的引导能够得到，正数都在原点的右边，负数都在原点的左边.

教师追问：还有什么发现？

师生活动：教师引导学生根据直尺的经验可以获得进一步的结论，并板书.学生在教师的追问下得出结论，即右边点表示的数大于左边点表示的数.

教师追问：可不可以再具体一点？

师生活动：教师在数轴上标出正数部分，0，负数部分，引导学生发现更加具体的结论.学生在教师的引导下发现，正数＞负数，正数＞0，负数＜0.

【设计意图】数轴本身就是数与形的结合，通过层层设问让学生感受数轴的作用，数轴形的直观得出数的规律，从数与形的角度体现数轴的作用.

5.运用规律，解决问题

问题1：数3所表示的点在原点的哪一边？与原点的距离是几个单位长度？

教师追问：-3呢？

师生活动：教师提出问题，学生思考回答，回答有误的，教师引导并加以分析.学生根据所学知识回答问题，回答错误的地方，经过教师引导，回忆柳树与槐树到汽车站牌都是3米，负号仅仅表示方向.

教师追问：若a是一个正数，则数轴上表示数a的点在原点的哪一边？与原点的距离是几个单位长度？-a呢？

师生活动：教师提出问题，引导学生在用字母代替数的情况下正确思考，得出正确分析.学生借助前面一例的经验，能够正确分析，并得到正确的结论.

问题2：若m是一个有理数，则数m表示的点可以在数轴上的什么位置？

师生活动：教师提出问题，并加以引导.学生回答，经过教师引导得出数m表示的点可以在原点的右边，原点的左边，还可以在原点上.

教师追问：请同学们在三个数轴上分别表示出来，并观察、比较数m与0的大小.

【设计意图】运用规律解决问题要由简到繁.从数字到字母的过渡是初中阶段代数学习的一次跨越.借助数轴这个图形对字母所表示的数加以理解，从具体到一般，让学生初步体会数形结合，以及分类讨论的数学思想.

6．归纳小结，概括新知

（1）这节课我们学习了哪些内容？

（2）通过本节课的学习，你对数轴有了哪些认识？

师生活动：教师引导学生参照提出的问题回顾本节课所学的主要内容，对知识进行及时的归纳梳理.学生根据自己的能力进行总结，回答不到位的地方由其他学生补充总结.

【设计意图】通过小结，让学生对已获得的知识进行梳理，培养学生归纳和概括的能力.

7．课后作业，巩固深化

教材第9页第2题和第3题，教材第14页第2题和第3题.

【设计意图】数轴是七年级阶段最为基础，又非常重要的知识内容，所以作业的题目要面向全体学生，落实人人都能获得良好的数学教育.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］人民教育出版社，课程教材研究所中学数学课程教材研究开发中心.《义务教育教科书·数学》教师教学用书（七年级上册）［M］.北京：人民教育出版社，2013.

［3］曹才翰，章建跃.数学教育心理学（第二版）［M］.北京：北京师范大学出版社，2007.

收稿日期：2015—12—12

作者简介：季军（1978—），男，中学一级教师，主要从事数学教育与中学教学研究.