创新推动课程改革 全面提高教育质量——暨“第九届初中青年数学教师优秀课展示与培训活动”总结

章建跃（人民教育出版社）



创新推动课程改革全面提高教育质量
——暨“第九届初中青年数学教师优秀课展示与培训活动”总结

章建跃（人民教育出版社）

第一部分：对本次活动的概要总结

一、概况

本次活动共有来自全国除西藏、港澳台以外的所有省、直辖市、自治区，行业的近2 700多名代表参加，覆盖范围广，受到全国初中数学教师、教育研究部门、各会员单位的高度重视.共有123位各地选拔的选手进行优秀课展示.

二、对活动满意度的调查

组委会在各分会场共发放问卷480份，回收问卷451份，有效问卷451份.

（1）对本次活动，您的总体评价是（）（1表示很不满意，5表示很满意）.调查结果如表1所示.

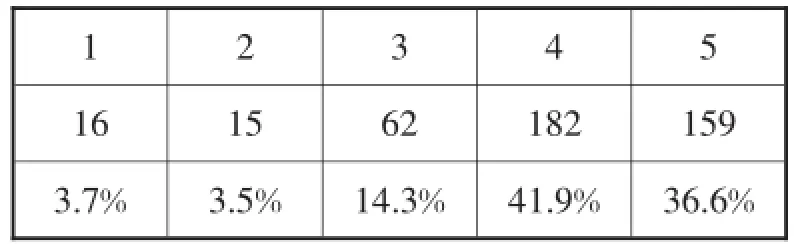
表1

（2）您最感兴趣的环节是（）.调查结果如表2所示.

表2

（3）您对评委点评的满意程度（）（1表示很不满意，5表示很满意）.调查结果如表3所示.

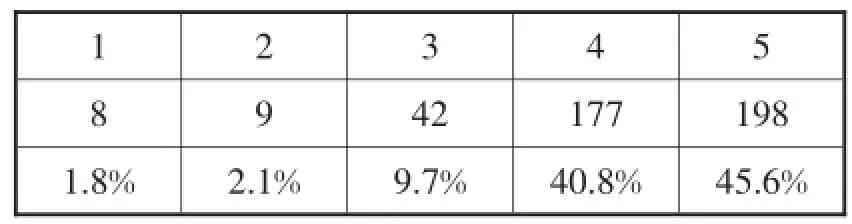
表3

上述数据表明，参会代表对本次会议的满意率较高.

三、本次活动的一些特点

（1）与以往相同，本次活动涉及我国当前使用的所有版本的初中数学教材.版本的多样化从一个侧面反映了本次活动的代表性和广泛参与性.

（2）内容覆盖了初中数学课程的所有板块，课型非常丰富，概念课、原理法则课、章小结课、习题课、复习课、综合实践课，还有专题课等.

教学内容的选择方面，许多选手都对自己提出高要求，敢于挑战难点内容，高难度的探究性、实验性课，在这次活动中占一定的比例.

（3）各位参赛选手在理解教学内容上下了很大功夫，与往届比较，在数学理解水平上有了很大进步.教学时力求揭示数学内容的本质，渗透数学思想方法.

教学设计比较好地体现了学会颁发的“标准”的要求，整体质量较高.

（4）学生主体意识进一步加强，注意创设体现数学知识发生发展需要、数学与生活联系的情境，使学生感悟数学知识产生的必然性；注重精心设计学生活动，采取问题引导学习的方式，让学生带着问题开展探索活动，将转变学生学习方式落在实处.

注重学生参与，教师力求精讲多问，将学生推向前台，让学生有主动学习的机会，教师采用追问等方式推动学生的数学理解.

（5）教学过程中，能自觉注意根据学生的认知规律安排教学活动.特别值得一提的是，许多参赛教师都能注意根据概念教学的基本规律安排教学进程，注意通过具体事例的归纳、概括活动得出数学概念.

对于“常规的概念课怎么上？”“什么叫概念的发生发展过程？”“什么叫概念教学中的思维教学？如何落实？”等问题，许多选手都进行了深入研究，本次活动产生了非常好的示范课.

（6）性质的教学注重整体性，提供一个清晰的研究脉络.例如，对于学会指定课题“平行四边形的性质”，重视章引言的教学，类比三角形的研究构建四边形的研究脉络.在研究性质时，从“图形的组成要素的位置关系和数量关系就是性质”出发，先发现平行四边形各种性质，再推理论证，并在小结时总结研究思路.

（7）多元评价方式的运用.大多数选手在展示和自述中，都提到了设计学生自我评价环节，学生的相互评价、改进、完善，以及教师肯定、表扬、纠正等，使评价发挥出促进学生发展，激发学生学习积极性和主动性的作用.

（8）注意多种教学媒体和教学手段的组合使用，信息技术与数学教学整合的水平进一步提高，大部分教师都力图做到恰当使用信息技术，帮助学生理解数学内容.

可以看到，全国各地硬件水平已经没有太大差异，信息技术工具、软件等呈现多样化态势.但教师的应用水平差距明显.

（9）本次活动的课题继续采取“自选动作+规定动作”的方式，“指定课题”采取“同课异构”的方式组织展示，同一课题四名教师执教，有利于观摩教师通过比较获得启发.

指定课题难度都是较大的，每名教师对内容的理解、教学处理各有不同，评委和观摩教师对这些课的看法多种多样甚至针锋相对，提出的观点也精彩纷呈，真正达到了研究、交流的目的.

（10）各位参加展示的教师都表现出很好的亲和力，自然大方，有激情.课堂气氛比较活跃、生动、有趣，增强了课堂教学的效果.

有的选手对“录像课展示与自述”到底展示什么、自述什么，理解很到位.

地区差异仍然明显，有些地方推荐的课还没有达到应有的水平.

本次活动在各地推选的基础上，评选出了25名最优秀选手，他们是：

沈艳秋（上海市普陀区曹阳中学附属学校），季军（新疆生产建设兵团第二中学），李静（山西省应县第三中学校），高洁（上海市李惠利中学），刘丹（吉林省延吉市第四中学），乐增光（浙江省宁波市北仑区小浃江学校），吴颖（北京市通州区第二中学），银玲（四川省德阳市第五中学），任静（重庆市万州区外国语学校），张冬梅（东北师范大学附属中学），黄宝瑛（江西省新余市第四中学），姜萌（黑龙江省大庆市第一中学），王用华（湖北省荆州市实验中学），王群（浙江省临海市学海中学），许萍（江西省崇义县章源中学），黄丽萍（四川省宜宾市南溪区南溪一中外国语实验学校），何广民（黑龙江省齐齐哈尔市第二中学），刘倩（江苏省连云港市连云区板桥中学），柴晓利（河南省郑州市第五十一中学），高晓微（内蒙古呼和浩特市实验中学），梁洪源（广东省珠海市斗门区实验中学），荣彬（四川省成都市石室中学），何颖（湖北省武汉市第一初级中学），李婷（河南师范大学属附中学），胡松（江苏省南京市第二十九中学初中部）.

（11）评委工作非常认真，他们事先观看了各位选手提供的完整的课堂录像，预先写好了点评提纲，有许多评委都是先做好ppt，再结合每一位选手的现场表现给予认真点评.

四、需要注意的一些问题

（1）课堂教学目标的研究和确定还不到位.教学设计中，仍有许多选手以“三维目标”分列、“知识技能，数学思考，问题解决，情感态度”分列、“知识目标，能力目标，情意目标”分列等方式呈现课堂教学目标，这是对教学目标理解不够、没有下力气研究的结果.

必须指出，“三维目标”是课程目标，不是课堂教学目标.实际上，学校教育目标具有层次性，从宏观到微观依次是：教育方针—课程目标—单元目标—课时目标.

另外，在目标的设定和达成之间存在比较明显的差距.

（2）缺乏对学习方式的研究，有效组织学生自主、合作学习的方法和指导的能力有待提高.

（3）引入环节刻意联系实际，不够自然；刻意设计探究、讨论等活动环节，等等.

（4）问题设计不合适的情况较普遍，问题提出后急于引导、提示，留给学生独立思考的时间和空间不够.

（5）教师讲得不得法的现象仍然存在，有些教师没有把有思维含金量、有思考价值的问题放手让学生思考，而是由自己包办代替了.

（6）小结用语中，“学了今天这节课，你有哪些收获？”仍然盛行，让人不知所云.

五、需要商榷的一些问题

（1）多数课都采用课前导学案，造成预设的环节过于充分，生成的环节过于顺畅，教学的重心过于前移，在某种程度上掩盖了学生独立思考和当堂训练落实的情况，造成课堂练习的进程太快，挤压了学生思考、交流的空间．

导学案泛滥是导致我国学生数学学习负担过重的原因之一.

什么叫做导学案？对这个问题应当加强思考.可以肯定的是，“概念、原理关键词填空+题目”不是导学案！

顾名思义，导学案就是引导学生学习的方案，而这里的“导”主要应该在思维的引导上，采用“问题引导思维”的方式，以“学习任务单”的形式呈现.“导学案”的内容主要有两个：一是启发学生思考、引导学生理解数学内容本质的问题；二是对重、难点或容易疏漏的方面的提示语.

编制导学案要把握的核心是：提好问题！

例如，“旋转的性质”导学案.

问题1：你认为研究旋转的性质就是要研究什么？

【设计意图】使学生明确研究的目标.研究旋转的性质，就是研究旋转前后两个图形的关系，探索“变化中的不变性”.

问题2：具体而言就是要研究什么呢？

【设计意图】使学生明确具体的研究思路.根据“几何学是研究几何图形的形状、大小和位置关系的学科”，就是要研究两个图形对应元素之间的形状、大小和位置关系等.

问题3：任意画一个△ABC，取一点O为旋转中心，将△ABC绕点O逆时针旋转30°.找出这个旋转中的对应元素，它们有什么不变性？

【设计意图】使学生养成有序思考的习惯，培养他们发现性质的能力——考查对应点、对应线段、对应角、对应面等的相互关系.

问题4：对应点的不变性怎么体现（提示语：如何利用三要素？）？你能说明对应线段的长度不变吗？

问题5：你认为还有什么不变性（图形中的位置关系保持不变，如垂直关系、平行关系等）？

（2）探究性学习如何组织？小组合作学习该怎么做？

首先要明确，数学学习需要独立思考.要在独立思考的基础上展开合作学习.

有难度的问题、有多种多样方法的内容才需要合作、讨论、交流.

第二部分：全面深化课程改革，落实立德树人根本任务

一、课改的背景和面临的任务

教育改革是社会发展改革整体中的有机组成部分，以国家社会发展改革为背景，要结合国家社会发展与改革的需要来思考.

当前，国家治理最根本的着眼点是深化综合改革，理顺各方面的关系.教育改革也要抓住深化、综合的要求而持续推进.

在十八届五中全会公报中，强调创新、协调、绿色、开放、共享的发展理念.提出“坚持创新发展，必须把创新摆在国家发展全局的核心位置，不断推进理论创新、制度创新、科技创新、文化创新等各方面创新，让创新贯穿党和国家一切工作，让创新在全社会蔚然成风”.要求“推动物质文明和精神文明协调发展，加快文化改革发展，加强社会主义精神文明建设，建设社会主义文化强国，加强思想道德建设和社会诚信建设，增强国家意识、法治意识、社会责任意识，倡导科学精神，弘扬中华传统美德”.对于基础教育，强调“开放发展，提高教育质量，推动义务教育均衡发展，普及高中阶段教育，逐步分类推进中等职业教育免除学杂费，率先从建档立卡的家庭经济困难学生实施普通高中免除学杂费，实现家庭经济困难学生资助全覆盖”.要求“全面贯彻党的教育方针，落实立德树人根本任务，加强社会主义核心价值观教育，培养德智体美全面发展的社会主义建设者和接班人.深化教育改革，把增强学生社会责任感、创新精神、实践能力作为重点任务贯彻到国民教育全过程”.“推动义务教育均衡发展，全面提高教育教学质量”.

显然，我国教育的规模问题已经解决.2010年《国家中长期教育改革和发展规划纲要（2010—2020年）》中提出，我国教育面临的主要任务是解决内涵质量的问题，解决育人模式改革的问题.这就需要在已有课改的基础上深化改革.而我们面临的问题错综复杂，许多都是两难问题，因此改革具有综合性，需要整体考虑.

二、数学课改的主要任务

十八大提出的“教育的根本任务在于立德树人”就是整个教育改革的核心任务.

如何把这个要求在数学教育中落实下来，在教学中体现出来，在课堂中实施下去？

我们认为，关键是要把“立德树人”的要求具体化，体现在教学内容和教学过程中，转化为一种可操作的行动，转化为数学育人的具体措施.

从教育部的顶层设计看，数学学科的“立德树人”目标，首先体现在数学学科的核心素养上.在《义务教育数学课程标准（2011年版）》中提出了八个核心概念：数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想，这些都可以看成是数学学科核心素养的要素.无论理论上如何界定，作为数学教育的实施者，广大一线教师应该加强思考的是，落实数学课改的核心任务，要有具体措施，要把数学学科核心素养的培育落实在数学教育的各个环节.

三、提升学生核心素养的思考点

首先要明确这样的观点：“学科育人”要依靠学科的内在力量.

“数学育人”要在数学内部挖掘育人资源，并使它们在数学教育的各个环节中发挥作用.为此我们要思考：数学学科独特的、别的学科不能替代的育人功能到底在哪里？

数学是思维的科学，推理、运算是数学的命根子.数学对于发展学生的思维特别是逻辑思维是至关重要的.也就是说，数学学科育人的独特功能，主要在培养学生的思维，特别是逻辑思维上，要使学生学会思考，特别是学会有逻辑的思考，使学生成为善于认识问题、善于解决问题的人才.

具体如何做？我们可以从“数学对象的获得—数学对象的研究—数学知识的应用”这三个方面（阶段），从数学思维的角度全面、综合地思考核心素养培育点.

数学对象的获得，要注重数学与现实之间的联系，也要注重数学内在的前后一致、逻辑连贯性，从这两个方面发现和提出问题，提升数学抽象、直观想象、归纳推理等素养.

对数学对象的研究，在分析研究对象的性质、内在规律的过程中，要注意发展学生的观察、分析、归纳、抽象、推理等水平，在对性质的证明过程中要注重培养学生的推理论证、运算求解的能力.

应用数学知识解决问题，要注重利用数学概念原理分析实际问题，体现建模的全过程，学会分析数据，从数据中挖掘信息等.

无论课改如何发展，“数学课要教数学”不会变，“数学课要教好数学”的要求也不会变.要做到这些，关键是要做到“两个过程”的合理性：数学知识发生发展过程的合理性，学生思维过程的合理性，这是落实数学学科核心素养的关键点.前一个“合理性”的核心是数学的学科思想问题，后一个“合理性”是学生的思维规律、认知特点问题.只要把握好这两个合理性，我们就可以做到“以不变应万变”.

第三部分：提高数学教学质量的关键点——对八个指定课题的解读

本次活动我们设置了八个指定课题，希望通过这些课题引领我国的初中数学课堂教学研究.下面对这八个课题的设计意图进行简要解释.

总体思路：

贯彻德育为先、能力为重、全面发展的教育理念，坚持启发式教学思想，变革教学方式，进一步推广自主、合作、探究的学习方式，与启发、讨论、参与的教学方式，增强数学育人的针对性和实效性.

在发挥数学的内在力量，使学生在掌握数学知识的过程中学会思考，成为善于认识问题、解决问题的人才上进行积极探索.

重点考虑在培养学生的创新精神和实践能力上有较大意义的、体现教育信息化要求的、普遍存在教学疑难的题目，并考虑代数、几何、统计与概率以及综合与实践等各领域的内容平衡.

一、系统观指导下的数学教学

系统观的内涵：

整体性——把研究对象看成一个整体，从整体出发，在组成系统的各要素相互关系中探究研究对象的本质和规律.

层次性——系统是由要素组成的整体；每个系统又是它的上位系统的组成要素，由此构成具有层级关系的整体，这就是层次性.先把握基本要素，再看要素组成的子系统，然后再看子系统组成的上位系统……这样才能具有思想性、观念性.

联系性——系统和系统之间、各要素之间、系统和要素之间是相互联系、相互作用的.任何事物都由若干部分、要素构成，各部分、要素相互依存、相互联系.只有这样，事物才能成为有机整体.任何事物都与周围的其他事物相互联系着，包括横向联系和纵向联系.

目的性——数学育人目标有一个从宏观到微观的层级系统.教学设计应该把教学过程看成具有一定发展规律和趋势的系统，在宏观目标指导下分析具体目标和内容，要注意把宏观目标落实在具体课堂中，使每一堂课都为达到宏观目标服务.

问题：数学育人目标的层级系统是怎样的？

宏观到微观的目标体系：教育方针—课程目标—单元目标—课时目标.

课堂教学中，三维目标是融为一体的，课堂教学目标设置的总体要求是：以教学内容为载体，过程中体现思想方法、思维能力的配演，努力挖掘内容所蕴含的育人资源，实现数学素养的逐步提升.

指定课题1：用配方法推导一元二次方程的求根公式.

课标要求：理解配方法，能用配方法推导一元二次方程求根公式.

本次活动提出的教学设计要求：体现单元设计下的课堂教学，即要在数学的整体观指导下，构建连贯的探索过程，以适当的问题引导学生自主发现推导求根公式的方法（配方法），并通过对公式的讨论培养思维的严谨性.

从整体上看，“一元二次方程的解法”的教学要点是基本策略和基本过程.

基本策略：降次，即通过配方、因式分解等，将一个一元二次方程转化为两个一元一次方程来解.

基本过程：根据平方根的意义，直接得出x2=p和（x+n）2=p的解法——通过配方，将一元二次方程x2+px+q=0转化为（x+n）2=p的形式再解——对方程ax2+bx+c=0配方后得出求根公式——特例：将ax2+bx+c分解为两个一次因式的乘积，则可令每个因式为0来解．

教学设计主线：

（1）宏观提问：我们面临的任务是什么？

解方程ax2+bx+c=0.

（2）什么叫解方程？你会解ax2+bx+c=0这类方程吗？我们会解哪些类型的方程？解这些方程的思想方法是什么？

（3）能否类比二元一次方程组的解法，给出解一元二次方程的思想方法？

二元一次方程组采用“消元”化归为一元一次方程，“一元二次方程”要采用“降次”化归为一元一次方程.

（4）从特殊到一般、从具体到抽象是基本方法，我们可以从具体方程的解法中归纳出一般思路.

①你觉得最简单的一元二次方程是什么？能举出一些你会解的一元二次方程吗？

用直接开平方的方法解x2=p.

②（x+n）2=p怎么解？

③x2+px+q=0怎么解？

④ax2+bx+c=0怎么解？

⑤有没有特殊的情况可以不用求根公式解？

二、构建研究几何性质的整体思路

首先应注意到，必须让学生明白“几何性质”到底指什么.只有明白了这个问题，才能使学生在独立面对一个几何对象时知道从哪里下手研究性质，才能使学生自主探究，才能使培养、发现和提出问题的能力落在实处.

一般而言，“性质就是一类事物共有的特性”之类的说法过于宏观，在具体思考中没有可操作性，需要针对具体内容进行归纳.例如：

运算中的不变性（规律性）就是性质——研究代数性质，“算算看”是基本方法；

变化中的不变性（规律性）就是性质——研究函数的性质，在运动变化中进行观察是基本方法；

要素和要素之间确定的关系就是性质——观察几何图形的构成要素之间的相互关系（位置关系、大小关系等）是研究几何性质的基本方法；等等.

那么，如何让学生知道“什么叫性质”呢？

我们可以引导学生对已知的关于某个几何图形的性质进行归纳，由此得到几何图形性质的表现方式，进而概括出研究性质的方法.例如，三角形是最典型的几何图形，我们可以让学生思考如下问题：

（1）从三角形的“内角和为180°”“两边之和大于第三边”“大边对大角”“等边对等角”等你想到了什么？

内角、边都是三角形的组成要素，这些性质都表明了“三角形要素之间的某种确定的关系”.

一般地，几何对象组成要素之间确定的关系就是性质.

（2）从“外角等于不相邻两内角的和”“三条高交于一点”“等腰三角形三线合一”等又想到了什么？

把外角、高、中线、角平分线等叫做三角形的相关要素，这些性质表明了“相关要素”之间的某种确定的关系.

一般地，要素、相关要素之间确定的关系就是性质.

另外，这里的“关系”是指大小关系、位置关系.

指定课题2：平行四边形性质的探索与证明.

课标要求：探索并证明平行四边形的性质定理：平行四边形的对边相等、对角相等、对角线互相平分.

本次活动提出的教学设计要求：在明确“什么是图形的性质”的基础上，通过类比三角形的性质，从整体上提出平行四边形性质的猜想，给出证明，要体现研究几何问题的基本套路，渗透推理的基本思想.

为什么要提出这样的教学设计要求？这样做有什么好处？

（1）立意高，思想性强，“数学味”浓；

（2）反映数学知识的发生、发展过程，是自然而水到渠成的；

（3）探索性更强，能更好地落实“发现和提出问题的能力、分析和解决问题的能力的培养”，创造性也更强；

（4）符合数学思维规律，体现数学的整体观，使性质的发现具有必然性，能给学生更多智慧的启迪，思维的教学更加到位；

（5）更能体现学习的自主性，更能激发学生的学习主动性.

为什么可以这么做？

首先，学生已经完整地学过三角形，已经了解了研究一个几何对象的基本套路：以三角形的要素（三条边、三个内角）、相关要素（高、中线、角平分线、外角等），以及几何量（边长、角度、面积等）之间的相互关系为基本问题，从“形状、大小和位置关系”等角度展开研究，因此与学生的认知准备相适应.

其次，只要教师在研究方法上加以引导，通过类比使学生意识到，研究平行四边形的性质，就是研究平行四边形的四条边、四个内角、对角线等之间的大小关系、位置关系，就可以容易地得到有关性质的猜想.

本次活动中，担任这一指定专题的教学研究的王用华、王群老师的课都非常清楚地表明，在上述思想指导下，学生都能得到自己的发现，而且得到了许多教材上没有给出的性质.

指定课题3：探索并证明圆的切线长定理.

课标要求：探索并证明切线长定理：过圆外一点所画的圆的两条切线长相等.

本次活动提出的教学设计要求：体现“探索”，包括探索思路的构建——研究几何对象的“基本套路”；处理好“探索”与“证明”的关系.

这里我们先来看看如何研究圆的性质.

根据上面给出的研究几何图形性质的教学思路，应该先让学生明白圆的要素、相关要素.例如，圆心、半径、直径、弧、弦、圆心角、圆周角……

思考：怎样引导学生发现和提出值得研究的命题？

整体而言就是要引导学生归纳地提出猜想，在面对一个新的几何对象时，能依据已有的研究几何图形性质的套路展开思考，并且要注重思维的逻辑性，有序地探索性质，使“发现性质”成为必然.

例如，圆的两条弦有什么“确定的关系”？

大小关系：与概念联系起来，得到“一个圆中等弦的弦心距也相等，反之也对”，“离圆心越近弦越长”“直径最长”.

位置关系：平行、相交（特例是垂直），容易得到许多性质.例如：

平行：两条平行弦所夹的弧相等；

垂直：垂径定理，让垂直于直径的弦平移到切线的位置，容易发现切线定理；

相交：相交弦定理，让交点动起来，移到圆上、圆外得到相交弦定理的各种变式；

交点在圆外时，再让弦移到切线的位置，就有“过圆外一点引圆的切线，有且只有两条，而且切线长相等”，这就是本指定课题的内容.教学设计中，如果能从以上思路加强思考，那么就能较好地体现“探索”.实际上，要让学生学会探究，教师自己首先应学会探究.

以上是圆与直线的位置关系，还可以研究圆与圆的位置关系.

题外话：如何看待选学内容？

本课内容属于“选学”，顾名思义，就是要让那些感兴趣的、学有余力的学生学.我们认为，类似这样的内容可以让所有学生学，关键是教师怎样教、学生怎样学.

令人担忧的是，实际教学中，因为选学内容不能作为升学考试的内容，因此“选学=不学”.

如果总是以“考与不考”作为“教与不教”的判断标准，让所有学生都只学最低标准的内容，这是一件非常可怕的事情——创新人才的培养无法落实.

三、认知观指导下的概念教学

首先要认识到概念教学的意义，前面已经提到，数学学习大致可以分为“获得数学对象—研究数学对象的性质—应用”三个阶段，获得数学对象是第一步.显然，如果连研究对象是什么都不清楚，那么对它的性质的研究将是无本之木.而“获得研究对象”的含义就是把握了研究对象的内涵、本质，也就是把握住了数学概念.因此，理解概念是数学学习的首要任务.

关于概念学习和教学，数学认知心理学、数学教育心理学已经有比较成熟的理论，其中要特别注意：

概念的学习主要靠归纳思维，概念教学要用归纳式.

概念教学要遵循一定规律，这是由数学概念的发生、发展过程和学生认知概念的思维过程所决定的.

概念课的教学设计，主要任务是：选择典型、丰富的具体实例，设计归纳具体实例的共同特征、抽象出本质特征，并概括到同类事物中去的过程.

概念教学的基本环节是：

概念的引入——借助具体事例，从数学概念体系的发展过程或解决实际问题的需要引入概念；

概念属性的归纳——提供典型、丰富的具体例证，进行属性的分析、比较、综合，归纳不同例证的共同特征；

概念的明确与表示——下定义，给出准确的数学语言描述（文字的、符号的）；

概念的辨析——以实例为载体分析关键词的含义（恰当使用反例）；

概念的巩固应用——用概念做判断的具体事例，形成用概念做判断的具体步骤；

概念的“精致”——纳入概念系统，建立与相关概念的联系.

指定课题4：数轴概念的教学.

课标要求：建立数轴的概念，能用数轴上的点表示有理数.

本次活动提出的教学设计要求：体现以“概念形成”的方式设计教学的基本环节，通过适当的问题情境引导学生体会数形结合思想.

关于本课的教学设计，这里想强调的是“理解数学”，就是要正确理解数轴的概念，其中核心是要抓住“三要素”的内涵：

①原点↔0（原点是区分方向的“基准”，0是区分正负的基准）；

②单位长度↔1（单位长度是度量线段长度的单位，1是实数单位，“单位”实际上给出了一个统一的标准，使大家在同一个平台上讲话）；

③方向↔符号（空间中，“由点A到点B”和“由点B到点A”是两件不同的事情，其差别由“方向”来标记.A，B两点“位置差别”的定量化定义，必需且只需用“方向”和“长度”.数轴上，方向只有“左”“右”两种，可以理解为“相反方向”.负数的引入是应描述现实中的“相反意义的量”之需，确定一个实数，需要“符号”和“绝对值”两个要素，它们正好对应了定量化定义A，B两点“位置差别”的“方向”和“长度”）.

在上述理解的基础上，再结合学生的认知基础进行教学设计.设计中要关注如下问题：

①“建立数轴概念”实质是理解数轴“三要素”，知道可以用数轴上的点表示数.

②什么叫“三要素”？——原点、方向、单位长度缺一不可.

③如何使学生体会到缺一不可？

以“概念形成”的方式设计教学的基本环节，通过适当的问题情境引导学生体会数形结合思想.具体要点是：

以现实问题情境——马路上的事物为背景，提出如下问题.

问题1：能否画图表示这一情境？

第一次抽象，画一条直线，在直线上标物体及距离.

问题2：怎样用数简明地表示这些树、电线杆与汽车站牌的相对位置关系（方向、距离）？从数学的角度分析、归纳本质特征，实现第二次抽象.

问题3：温度计等现实事例，在上述思路的引导下，归纳共性.

给出数轴的定义（第三次抽象）.

概念辨析——原则上应该是针对“三要素”，让学生明确只有在原点、方向、单位长度都确定后，数轴才唯一确定，可以采用比较的方法.

巩固性应用——重点是根据实际问题的需要选择原点和单位长度.

概念的精致——在后续学习中完成.

四、提高学生的思维参与度

数学是思维的科学，概念是思维的细胞，数学思维更是用概念思维，因此数学是培养思维能力的最佳载体．

为了培养学生的创造性思维，必须让学生有实质性的数学思考.

从数学知识发生发展、自然拓展过程，数学性质的合理猜想与论证过程出发，通过适当的问题引领，就能实现这样的目标.

具体怎么做？如下几点要引起注意：

（1）加强一般观念的指导作用，提升思想性.例如，前面提到的“几何图形的要素与要素的相互关系就是性质”“运算中的不变性就是性质”等就具有这样的作用.

（2）通过具体事例的归纳概括，特别是让学生自主探究、交流，给学生表达的机会，从表达中把握学生的思维过程，捕捉生成性教学资源，并用“你是怎么想的？”“你是怎么想到的？”“能把你的想法说得更清楚一些吗？”等促进思考，逐步培养学生用概念解释数学对象、通过归纳发现数学规律的能力与习惯.这是促使学生深层次参与课堂教学的有力举措.

（3）要把实质性的归纳机会留给学生，如具体实例共同特征的归纳就应该让学生完成.

指定课题5：整数指数幂.

课标要求：了解整数指数幂的意义和基本性质.

本次活动提出的教学设计要求：体现从指数概念和运算性质的扩充过程，注重知识的产生、发展过程，注重学生的思维参与度.构建一个前后一致、逻辑连贯的代数学习过程，使学生在掌握知识的过程中学会思考，把学生培养成为善于认识问题、解决问题的人才.

（1）本课之前学生已经学过的相关内容有如下两点.

①正整数指数幂的意义和运算性质，其中关键是am÷an=am-n和a0=1（a≠0）；

②分式的概念和性质、约分，分式的运算等.

说明：因为经过一定的时间，学生可能对这些知识的获得过程已经淡忘，所以要问一下“我们是怎样得到这些性质的？”，着重让学生说明这些性质和规定的合理性，特别是规定a0=1的合理性.

（2）接下来的教学，要利用正整数指数幂和有理数的学习经验，以运算引发问题，引导学生自主构建推广过程，获得有关法则和性质，这是提高思维参与度的关键.

向负整数指数幂的推广过程，与得到a0=1（a≠0）一致，关键是让学生把分式的约分和正整数指数幂的性质（am÷an=am-n（a≠0）） 联系起来，通过具体事例的归纳，感受a-n=（a≠0）的合理性.

（3）推广到负整数指数幂后，接着该干什么？

类比“数及其运算”可知，应该研究整数指数幂的运算性质.如何研究呢？数学推广的特征是“保持原来有的性质不变”，所以要研究在已有规定下，正整数指数幂的性质是否在整数范围内仍然成立，就如在有理数范围内讨论自然数系的运算律是否成立一样.

在推广后，这些性质的合并、简化——类似于引入负数后的加减统一，引入负整数指数幂后，乘除也就统一了，于是原来的五条性质可以合并成三条.

五、想象力与创新意识

显然，在学生成长过程中遇到的大量问题都不会有现成答案.解决这样的问题需要具备想象力，要能调动自己的知识经验，在头脑中反复地实验，动手试验，取得经验，然后筹划出方案.所以，想象力可以使学生学会事先筹划，从而选定一个比较完善的方案，这对提高办事效率和成功率都有极大好处.

想象力是一切灵感与发现的源泉，是一种极为宝贵的智力品质.科学家们总是以现有技术和理论为依据，通过想象进行假设，通过假设进行推理，得到科学假说，再通过实验和实践得到验证，从而确立为新的理论.

丰富的想象使感知敏锐、观察细致，而敏锐的感知和细致的观察又使人的想象更加丰富和深刻.

指定课题6：反比例函数的图象的性质.

本次活动提出的教学设计要求：既要体现研究函数图象与性质的一般思想方法和过程——已有的研究经验有哪些？又要注意通过适当的问题激发学生的创新思维，启发学生“由数想形”“由形助数”——怎样利用这个函数的特性，创新研究方法？

以往研究函数的性质，都是“先描点作图，再观察图象得出性质”.本课的教学，因为反比例函数图象作图较难（主要是图象的趋势、对称性等不明确），但函数表达式比较简单，所以应该利用代数知识先做些分析.

这样的做法与“常规”有所不同，为什么可以这样做？有什么好处？实际上，因为从代数表达式得出的上述特征，对于学生想象函数图象的特征很有帮助，可以让学生在画图之前就对图形的分布区域、变化趋势等有一个大致的轮廓形象.

为了引导学生发现函数图象的对称性，可以通过具体取值，并让学生思考该如何取点.例如（1，1），（－1，－1）；都满足表达式，它们有什么特点？再让学生把这些点描出来，这样就可以通过这些点的对称性而发现图象的对称性.

在以上探索的基础上，再取点、描点、作图，这样作出的图形就比较符合要求了.

六、“做数学”与学会学习

为了使学生学会学习，必须切实改进学习方式、教学方式.我们要改变“一个定义，三项注意，几个例题，大量练习”的做法，改变埋头苦干做重复性训练的被动学习方式，注重调动学生的所有感官，动手触摸、动眼观察、动脑思考，通过丰富多彩的学习活动、长时间的“悟”，然后有所发现.

使学生自我掌控学习过程，获得研究数学问题的切身体验，逐步达到对数学内涵的实质性理解，这是学会学习的应有之义.在教学活动中，要使“实验活动—数学抽象—逻辑表达”得到充分体现.

指定课题7：数学实验教学.

本次活动提出的教学设计要求：以图形的变换（对称、平移、旋转或翻折）为主题，设计合理的实验过程，让学生运用有关工具（如纸张、剪刀、模型、测量工具、作图工具以及计算机等），通过动手操作、独立思考和合作交流等活动“做数学”，经历知识的归纳、概括过程，获得实验对象的数学内涵，并抽象出数学原理（概念、性质等）.

教学设计与实施中，要注意从教学方式、学习方式的改进，数学活动经验的积累等方面加强思考．

关于数学实验的育人价值，我们在对江苏省南京市第二十九中学初中部胡松老师的“几何图形”一课的点评中有详细论述.

七、大数据时代的数学教育变革

“统计与概率”所涉及的数据应该是观察、试验、记录、调查的手段获取的客观数据.在大数据时代，数据不仅包括观察、试验、记录、调查的手段获取的客观数据，还包括对网络、文本、声音、图像等反映的信息进行数字化处理所获得的数据.在“统计和概率”的教学中，我们应当特别关注数据的获取、数据的统计特征表示，培养学生对数据的“看图说话”能力，提升归纳推理、数学建模、直观想象和数据分析等素养.

指定课题8：随机现象的变化趋势.

本次活动提出的教学设计要求：通过表格、折线图、趋势图等，感受随机现象的变化趋势.

要注重通过适当的问题，引导学生体会样本和总体的关系，体会用样本推断总体的思想，渗透数据分析意识.

结束语：“数学育人”的核心是培养学生的思维能力.

我们反复强调，数学学科的不可替代性在于它培养学生的思维（特别是逻辑思维）能力，这也是数学育人的核心所在.

数学育人目标的实现，教师是关键.其中，提高“理解数学”的水平是重中之重.

“理解数学”有三重境界：知其然，知其所以然，何由以知其所以然.第三重境界是要解决“如何思考”的问题.例如，对于三角形的角与角的关系，知道“内角和为180°”是“知其然”；会“添加辅助线证明内角和定理”是“知其所以然”；解决了“如何想到研究内角和”“如何想到添加辅助线”的问题，就解决了“何由以知其所以然”，实际上是在“发现和提出问题的能力”上有了扎实的基础.只有这样，才能在“思维的教学”上做到游刃有余.教师要学会“示以学生思维之道”的方法，要让学生在自己独立面对问题时“想得到，做得到”.

在培养学生的思维能力方面，有一些基本观念要树立起来.例如：

慢下来，给学生“悟”的时间和空间，“慢”就是快！实质性的数学思考是需要时间的.

应加强动手、思考和感悟的实践，培养学生渴求知识的感觉.

真正的学习必须经历“感知—感悟—知识”的过程.先让学生思考、感悟，经历“猜想—验证”“发

现—论证”的过程，然后上升为理性认识.

越是看上去简单的知识，越要让学生亲身感悟，使学生从中获得“如何思考”的体验，这样得到的知识才能转化为认识世界的智慧，创造力的培养也蕴含其中.

学生冥思苦想不得其解，一经提示又恍然大悟，问题到底出在哪里？“不是做不到，而是想不到”的现象，正是数学素养低、数学能力差的表现.改变这种状态，要让学生不仅能做而且会想，唯一的办法是放手让学生自己先想、先做，教师在如何想、如何做上加强引导.这就要限制课堂容量，放慢教学节奏，给学生“悟”的时间，给学生说出自己想法的机会.

教之道在于“度”，学之道在于“悟”.

为了发展学生的创新智慧，需要思考一些基本问题，例如：

如何用有趣的问题引发学生兴趣，用恰时恰点、直击要害、反映本质、简明易懂的问题引发学生思考、讨论？

如何不急不躁，给学生充分的时间开展独立思考、讨论交流？

如何提高解题的层次，使学生通过解题认识一般的数学原理，并让学生体会“如何做研究”，使思维的训练、创造力的培养蕴涵其中？

教学中应多问“你是怎么想的？”“你是怎么想到的？”“还有别的想法吗？”少问“是不是？”“对不对？”更不要“我已经给大家准备好了，下面开始算吧！”

必须清楚，通过技巧训练迅速提高分数，与通过思维训练全面提升能力，是两个完全不同的追求！

当前，数学课改已进入关键时期，各种思潮层出不穷，有点令人眼花缭乱.我们认为，大势所趋是：回归数学教育的本来面目，着眼于学生的长期利益，发挥数学的内在力量，挖掘数学内容所蕴含的价值观资源，以发展学生的思维（特别是逻辑思维）能力、培育理性精神为核心，使学生在掌握数学知识的过程中学会思考，成为善于认识问题、解决问题的人才.

只要我们在“理解数学，理解学生，理解教学”上狠下功夫，使自己的教师专业化达到较高水平，就一定能做到以不变应万变.

愿我们共同努力！

收稿日期：2015—10—09

作者简介：章建跃（1958—），男，编审，主要从事数学教育心理，数学课程、教材、教法等研究.