双基地声纳混响建模分析

陆　扬，薛　飞，张世海，王雪松

(中国人民解放军91439部队，辽宁 大连　116041)



双基地声纳混响建模分析

陆扬，薛飞，张世海，王雪松

(中国人民解放军91439部队，辽宁 大连116041)

摘要：在浅海环境下，混响是影响双基地声纳系统性能的主要因素，基于双基地声纳的几何特点，对接收端的混响进行了建模，并在接收端具有指向性的条件下，得出了混响面积以及接收端信混比的计算公式，对不同条件下接收端的混响强度以及信混比的变化进行了仿真分析，得到了不同条件下双基地声纳接收混响强度与收发位置、信号脉宽以及接受指向性的关系。

关键词：双基地声纳；混响强度；信混比

本文引用格式：陆扬，薛飞，张世海，等.双基地声纳混响建模分析[J].兵器装备工程学报，2016(6):129-131.

Citation format:LU Yang, XUE Fei, ZHANG Shi-hai, et al.Modeling and Analying for Bistatic Sonar Reverberation[J].Journal of Ordnance Equipment Engineering,2016(6):129-131.

伴随着新的降噪技术在潜艇上的应用，被动声纳的探测效果受到了很大影响，而对于主动声纳，在获得目标探测结果的同时，其自身也将暴露，这对其安全是非常不利的。双/多基地声纳由于其收发分置，接收端只是被动的接收目标回波信号，所以具有极好的隐蔽性。双/多基地还具有探测距离大、配置灵活以及抗干扰能力强等优点，因此成为声纳研究的热点[1-4]。

混响是由海面、海底的不平整性和海洋中各种非均匀性散射元的散射引起的，混响可分为体积混响和界面混响[5]，其中由海面、海底的散射产生的界面混响为主动声纳的主要干扰之一。对于收发合置声纳混响的研究已经有很多理论及计算方法，对于双基地声纳的混响国内外学者也进行了一定的研究[6-8]。本文以双基地声纳为基础，建立了海底混响的几何模型，分析了不同条件下双基地海底混响的强度以及接收信混比的变化，得到了双基地混响的衰减规律。

1　双基地声纳模型

1.1双基地声纳几何模型

如图1所示，忽略深度的不同，假设收发端及目标均在同一水平面上，R和S分别为接收端和发射端，收发端之间的距离为基线长度L，目标T的坐标为(x,y)；在水平面内，以收发连线为x轴，建立直角坐标系，目标到声源和接收端的距离分别为Rs和Rr，设声波在水中的速度恒为c，声波从声源S到目标T再传播到接收端R的时延为t。由于收发端为椭圆的两个焦点，目标位于椭圆上，在接收端估计出目标与基线的夹角θ0后，根据椭圆方程可求得Rr：

(1)

收发端的坐标可以通过GPS确定，通过估计得到的θ0和Rr即可以得到目标的坐标。

图1　双基地声纳几何分布

1.2双基地混响计算

假设海水是均匀的，海底散射系数为常数，只考虑对混响贡献较大的海底散射。由于考察的是浅海远程混响，所以假设收发端与界面散射元在一个平面上。在任意时刻t，接收到的混响为图2中的两个椭圆之间的环带的散射波组成， 假设声波按球面波扩展，则此时接收端的混响强度[9]可以表示为对混响有贡献的散射面元的积分，如下式所示

(2)

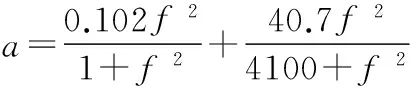
图2　对接收主瓣有贡献的混响面积

此时接收端的混响不仅与发射信号的脉宽及收发端的位置有关，还与发射端与接收端的波束宽度有关，假设发射端无指向性、发射信号脉宽一定，此时混响的面积将由接收波束与等时椭圆的相交面积决定，并且接收波束图上不同角度的增益是不相同的，如图3所示。计算式中引入增益函数g(θ),它是一个混响入射角度θ与指向角度θ0的函数，主波束内|θ-θ0|的值越大，g(θ)越小，此时混响强度的表达式为

(3)

式中：φ为主波束宽度；在信号脉宽为T时，积分半径R1和R2分别由下式确定

(4)

不考虑主波束内不同角度上增益的差别，当脉宽不大的情况下，认为积分区域内声波的传播损失基本相同[10]，此时接收端的混响强度可表示为

(5)

RL=SL+10logμ-TLr-TLs+10logS

(6)

其中:SL为声源级，TLs和TLr分别为声波从声源到目标以及从目标到接收端的传播损失，而接收到的目标回波信号强度可表示为

(7)

其中μ0为目标的反射系数，将式(7)除以式(5)，取对数并化简，得到信混比

(8)

图3　接收阵主波束

2　仿真分析

假设无指向性发射声纳声源级为200 dB，声速c=1.5 km/s，基线长度L=8 km，探测信号的中心频率为f=5 kHz，信号脉宽为20 ms，海底散射系数设为μ=10-3,以收发连线为x轴，其水平垂线为y轴，接收端为坐标原点R(0,0),发射端的坐标为S(L/2,0)，不考虑声纳收发端和目标深度的差异[9]，接收基阵为20个阵元组成的直线阵，采用恒旁瓣算法，主波束宽度约为17°。考虑到主波束内不同角度的增益差别以及忽略此差别分别求得接收端混响强度，考虑到对称性，目标与基线的夹角为θ0=(0,180)°，仿真结果如图4所示。

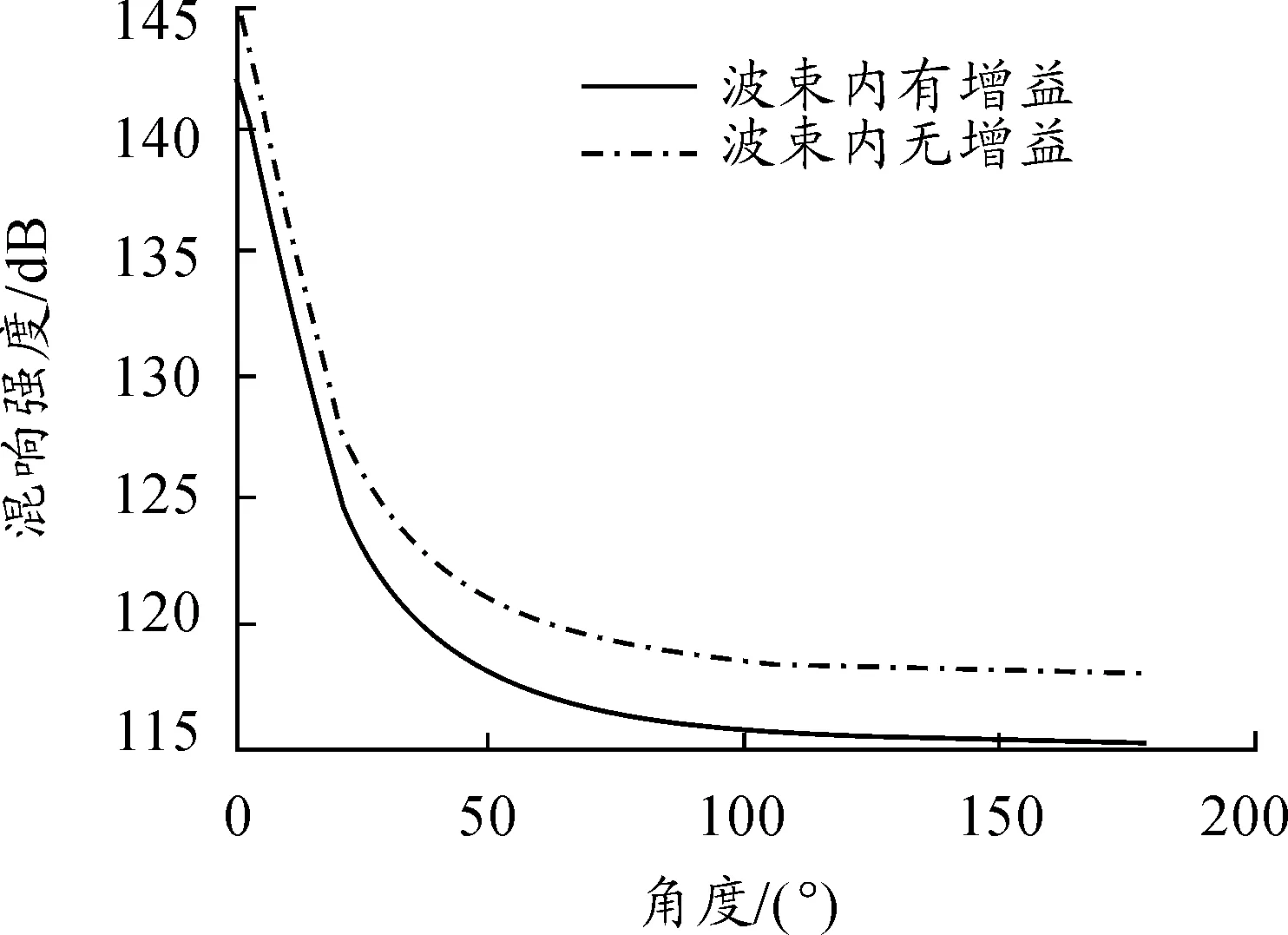
图4　两种方法求得的混响强度

从图4中可以看出，两种方式求的混响强度相差约为2dB，差别并不明显，所以在计算能力有限以及对混响值要求不很精确的情况下，可以忽略主波束内角度增益的差别。

当有目标存在的时候，假设其反射系数为μ0=10-1，当声传播时间 t=6ms，信号脉宽T分别为20ms和40ms，目标与基线的夹角为θ0=(0,180)°时，混响的面积以及接收端信混比的变化如图5、图6所示。从两图可以看出，随着目标与接收端夹角的增加，对接收主瓣内混响有贡献的面积越来越小，则接收端的信混比变大，对于发射信号而言，信号的脉宽越大，对接收主波束混响有贡献的散射面积也越大，相应的信混也就越小。

图5　混响面积随方位角变化曲线

图6　信混比随方位角变化曲线

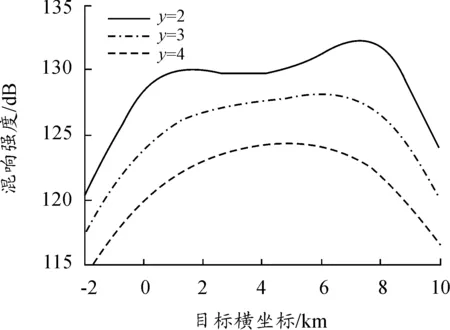
图7　目标不同位置时的混响强度

图8　信混比随目标位置变化曲线

当目标的横坐标从-2km到10km变化的过程中，不同纵坐标对应的混响强度以及信混比的变化如图7、图8所示。从图7可以看出，传播距离越短混响强度越大，其极大值出现在发射端处，这是由于此时混响面积最大。在图8中，曲线在接收端附近取得最大值，随着目标横坐标的增加信混比一直下降，取得最小值后又有一定的增加。出现这样的情况是由于在接收端附近，散射面积取得最小值，而随着目标横坐标的增加混响面积不断增大，在取得最大值后又变小，所以信混比产生了起伏。

3　结论

本研究对浅海中双基地声纳的混响进行了二维建模仿真，分析了散射面积、混响强度以及接收端信混比的变化规律，对于利用双基地声纳的机动性，合理地选择收发装置的机位具有一定的指导意义。在仿真计算中均未考虑海水的不均匀性与海底的不平整性，在以后的研究中，有待于更精确模型的提出。

参考文献：

[1]WILLETTPETER，CORALUPPISTEFANO.ApplicationoftheMLPDAtobistaticsonar[C]//Proceedings2005IEEEAerospaceconference.BigSky，MT，US:InstituteofElectricalandElectronicsEngineersComputerSociety，2005:1559498.

[2]QUIJANOJE，ZURKLM.Useoftheinvarianceprinciplefortargettrackinginactivesonargeometries[C]//Oceans2006.Boston:InstofElecandElecEngComputerSociety，2006:4099007.

[3]惠娟,王自娟,惠俊英,等.双基地混响平均强度理论及仿真预报[J].物理学报，2009，58(8)：5491-5500.

[4]张瑶.浅海主动声纳目标探测若干方法研究[D].哈尔滨:哈尔滨工程大学，2013.

[5]刘伯胜,雷家煜.水声学原理[M].哈尔滨：哈尔滨工程大学出版社,1993.

[6]DALED，DVANCECROWE.Bistaticreverberationcalculationsusingathree-dimensionalscatteringfunction[J].Acoust,1991,89(5):2207-2214.

[7]KEVINL，WILLIAMS，DARRELLR,etal.Bistaticbottomscattering:Model，experimentsandmodel/datacomparison[J].Acoust.Soc.Am,1998,103(1):169-181.

[8]笪良龙,刘贝,张林,等.收发深度变化对浅海混响的影响研究[J].指挥控制与仿真，2009,31(3)：58-60.

[9]惠俊英,生雪莉.水下声信道[M].2版.北京：国防工业出版社,2007.

[10]李明达,李桂娟,惠俊英,等.海底混响背景对双基地水声探测影响的估算[J].装备环境工程,2008,5(2)：21-24.

(责任编辑杨继森)

doi:10.11809/scbgxb2016.06.030

收稿日期：2015-12-23；修回日期：2016-01-22

作者简介：陆扬(1966—)，男，博士，高级工程师，主要从事水声测控研究。

中图分类号：TB567

文献标识码：A

文章编号：2096-2304(2016)06-0129-04

Modeling and Analying for Bistatic Sonar Reverberation

LU Yang, XUE Fei, ZHANG Shi-hai, WANG Xue-song

(The No.91439thTroop of PLA, Dalian 116041, China)

Abstract:In the shallow water environment, the reverberation is the main factors that affect the performance of bistatic sonar, and based on the geometry distribution of the bistatic sonar system, this paper modeled the reverberation in the receiver, and under the condition that the receiver is directional, we deduced the equation of reverberation area and the signal-to-reverberation ratio(SRR), and simulated and analyzed the reverberation intensity and SRR in different conditions, and obtained the relationship of reverberation with the sonar position, impulse width and the receiver’s directivity.

Key words:bistatic sonar; reverberation strength; signal-to-reverberation ratio