基于BP神经网络的高寒山地弹药消耗需求分析
2016-08-12齐浩淳黄大鹏魏久南陈志刚
齐浩淳,黄大鹏,魏久南,陈志刚
(1.中国人民解放军68129部队,兰州 730060; 2.中国人民解放军军械工程学院,石家庄 050003)
基于BP神经网络的高寒山地弹药消耗需求分析
齐浩淳1,黄大鹏2,魏久南1,陈志刚1
(1.中国人民解放军68129部队,兰州730060; 2.中国人民解放军军械工程学院,石家庄050003)
摘要:采用BP神经网络方法,建立了高寒山地弹药消耗量预测模型,对模型的预测流程和步骤进行了描述;结合高寒山地实际,对高寒山地弹药供应保障的消耗量需求进行分析。预测结果表明,所建立的弹药供应保障消耗量需求模型能够很好地预测高寒山地作战中的弹药消耗量。
关键词:高寒山地;弹药消耗量;BP神经网络
本文引用格式:齐浩淳,黄大鹏,魏久南,等.基于BP神经网络的高寒山地弹药消耗需求分析研究[J].兵器装备工程学报,2016(6):97-101.
Citationformat:QIHao-chun,HUANGDa-peng,WEIJiu-nan,etal.DemandAnalysesofAmmunitionConsumptioninColdMountainAreasBasedonBPNeuralNetwork[J].JournalofOrdnanceEquipmentEngineering,2016(6):97-101.
随着信息化技术在现代国防建设以及局部战争中的广泛应用,作战方式越来越趋多元化,同时作战过程中弹药的消耗量也随之倍增。对于高寒山地的弹药供应保障来说,归纳、分析影响弹药消耗需求的诸类因素,如弹药性能、种类、数量、弹药供应保障对象等,并根据高寒山地实际作战条件和作战任务,精确获得弹药供应保障的相关数据,通过合理的数据处理方法,建立最优化的高寒山地弹药消耗模型是实现弹药供应保障需求的核心。
目前,国内外对弹药消耗量需求分析的研究主要集中于保障需求分析模型的建立与优化。常用到的弹药供应保障需求分析方法和模型有Monto-Carlo方法、神经网络模型以及支持向量机方法等。2005年,William等在其报告中对美国战时弹药需求数量的预测能力进行了分析与说明[1]。同期,在《美国海军陆战队地面弹药需求研究》报告中,相关学者对美国海军陆战队的弹药需求及相关策略进行了深入讨论[2]。2009年12月,美军发布了陆军条例AR5-13,对陆军弹药总需求过程与优化系统进行了详细规定[3]。Kamath和Aronis则采用Bayesian方法对其在实际应用中的需求进行预测[4-5]。文献[6]根据弹药供应保障任务,利用层次分析法(AHP)对弹药存储需求量进行了研究。俞杰等建立了弹药供应保障系统动力学模型,从总体上对战时双方兵力因素、武器因素以及各个作战阶段弹药消耗的规律作了有益的探索,总结得出了战时弹药消耗的本质规律[7]。另外,BP神经网络在单目标弹药需求量以及基于历史数据对弹药消耗量预测方面也得到了广泛的应用[8-10]。
本研究在相关研究的基础上,结合高寒山地实际,采用BP神经网络方法,对高寒山地弹药供应保障的消耗量需求进行分析。
1 BP神经网络原理
1986年由Rumelhart和McCelland等首次提出误差反向传播(errorbackpropagation,BP)神经网络模型[11]。该模型针对用户需求,通过选取合理的数据样本进行训练,并利用训练好的模型实现对未知结果数据的预测。
1.1BP神经网络的基本结构
BP神经网络由输入层、中间层(隐含层)和输出层构成,属于多层前馈网络[12]。通常,3层BP神经网络即可很好地实现对非线性映射的逼近。图1为3层BP神经网络的结构示意图[11]。
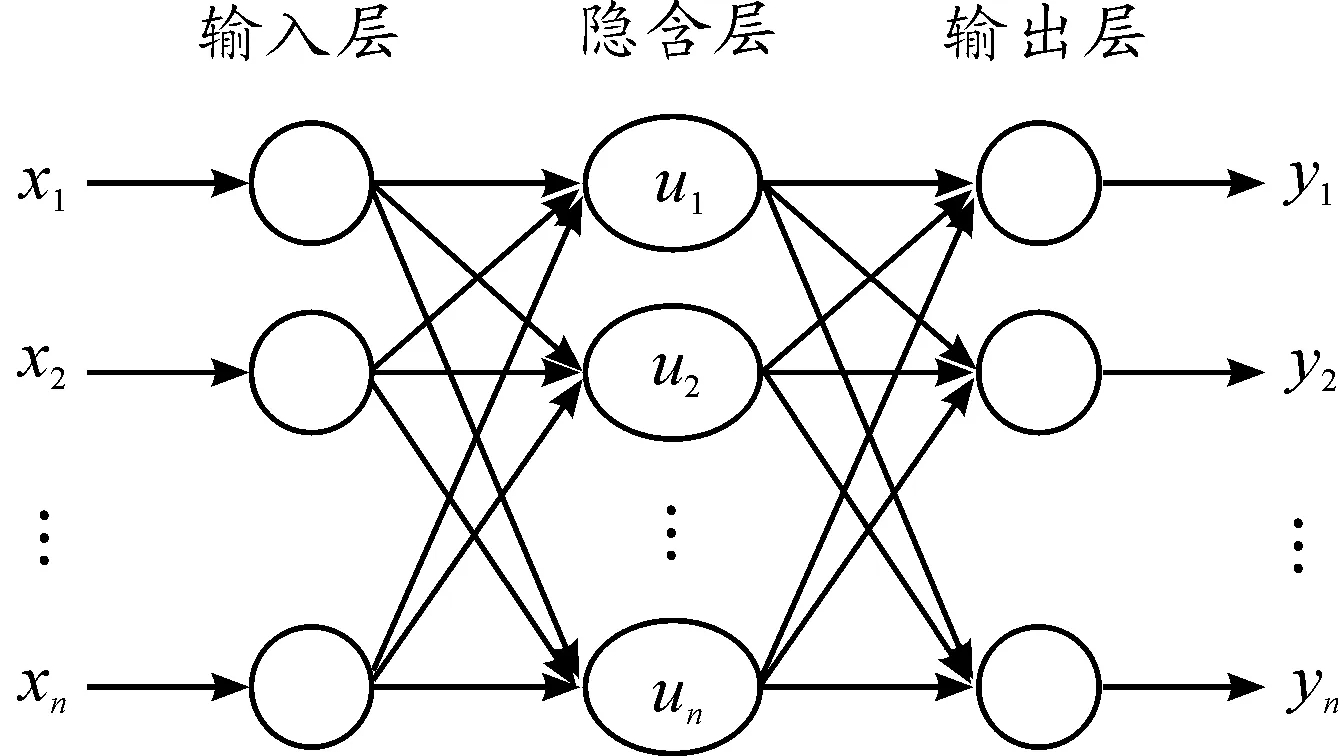
图1 BP神经网络3层结构
1.2BP神经网络的训练过程
正向传播和反向传播构成了BP神经网络的训练过程。在正向传播过程中,信号进入输入层并经过中间层对其进行处理,最后在输出层输出训练结果并对训练的输出值进行比较得到信号误差;在反向传播过程中,信号误差则由输出层向输入层传播。通常可以调整各层连接权值和神经元阈值来减小信号误差。对上述过程进行反复迭代,当网络的输出误差小于设定误差或者迭代次数达到设定的学习次数时,该训练过程结束,即可得到理想的连接权值和神经元阈值。
将3层BP神经网络的输入层、中间层和输出层神经元个数分别设定为n、m、q。设定输入层神经元的输入为xi(i=1,2,…,n),中间层神经元的输出为zj(j=1,2,…,m),输出层神经元的输出为yk(k=1,2,…,q),期望输出为tk(k=1,2,…,q),输入层至中间层连接权为wij(i=1,2,…,n; j=1,2,…,m),中间层至输出层连接权为vjk(j=1,2,…,m; k=1,2,…,q)。
BP神经网络的训练过程为:
步骤1:给定各个连接权值以任意小值;
步骤2:确定输入网络的学习样本;
步骤3:分别得出中间层神经元输出zj和输出层神经元输出yk为:
(1)
式中 f 为传输函数。
步骤4:分别得出输出层神经元误差δk和中间层神经元误差dj:
(2)
步骤5:对输出层和中间层的连接权进行调整:
(3)
步骤6:依次对其他学习样本,重复步骤3至步骤5,直到样本训练结束对其误差和进行判断,若满足精度要求或达到模型的最大训练次数,则训练结束;否则,继续对其进行修正。
1.3BP神经网络模型结构的确定
对于模型结构,为了提高网络的训练速度,模型选取只有一个隐含层的3层BP神经网络预测模型。输入、输出变量具体对应相应的输入、输出层神经元,因此对于具体的对象,可以设定相应的输入层神经元、输出层神经元个数。对于隐含层神经元个数的确定,得到:
(4)
式中:q为隐含层神经元的个数;n为输入层神经元的个数;m为输出层神经元的个数;a为常数,且1 此外,对于BP神经网络模型的各层激活函数,通常设置隐含层的神经元激活函数为tansig函数,输出层的神经元激活函数为线性函数。 2.1弹药消耗量数据的预处理 通过相关单位及文献,获取某型号弹药近几年的消耗量数据,将其视为单一时间序列,分别记作x1,x2,…,xn,需要预测的下一年弹药消耗量记为Ttest。对Ttest利用BP模型进行预测前,需要对弹药消耗量数据进行预处理,作为BP神经网络的训练过程和测试过程所用数据。分别将训练过程的输入数据、输出数据和测试过程的输入数据记作Ptrain,Ttrain,Ptest。将xk,xk+1,…,xk+s共计s+1个历史数据作为Ptrain中的第k个输入样本pk=[xk,xk+1,…,xk+s],xk+s+1作为第k个输出样本tk=xk+s+1。因此,第一个输入样本为p1=[x1,x2,…,xs+1],第一个输出样本为t1=xs+2;第二个输入样本为p2=[x2,x3,…,xs+2],第二个输出样本为t2=xs+3,依次得到n-s-2个输入样本组成输入矩阵Ptrain=[p1,p2,…,pn-s-2],与之相对应的n-s-2个输出样本组成输出矩阵Ttrain=[t1,t2,…,tn-s-2]。模型预测时,利用最近s+1年的弹药消耗量构造测试过程输入样本,表示为Ptest=[xn-s-1,xn-s,…,xn]。 2.2弹药消耗预测模型的训练与测试 对高寒山地的弹药消耗预测模型进行训练前,对获取的弹药消耗量数据进行数据预处理,从而得到BP神经网络训练过程的输入数据以及输出数据。利用BP神经网络对弹药消耗预测模型进行训练前,需要对神经网络的结构和训练参数进行设定。依次通过求取隐含层、输出层各神经元输出,求取期望值跟实际输出的误差,判断是否满足要求。同时,计算隐含层单元误差,求取误差梯度,调整权值等步骤训练BP神经网络模型;当期望值跟模型实际输出的误差达到设定值时,BP神经网络停止训练,继而得到训练好的弹药消耗预测模型。 通过利用Matlab软件,设定神经网络的最大学习迭代次数、训练速率和训练目标误差等参数,建立BP神经网络。 对高寒山地的弹药消耗量进行预测时,首先获取最近s+1年的弹药消耗量,并将其作为弹药消耗预测模型的测试数据。将处理好的数据输入到训练好的模型中,最终得到弹药消耗量的预测数据,实现对未来年份的弹药消耗量的预测。 2.3弹药消耗预测流程 从上述步骤可以得出弹药消耗量预测模型的具体流程,如图2。 模型训练过程的步骤为: 步骤1:获得弹药消耗量数据,并且对数据预处理获得模型的训练过程输入数据和输出数据; 步骤2:确定BP神经网络的结构和训练参数; 步骤3:依次通过求取隐含层、输出层各神经元输出,求取期望值跟实际输出,求取两者误差值,判断是否满足要求、计算隐含层单元误差,求取误差梯度,调整权值等步骤对BP神经网络进行训练; 步骤4:当期望值跟模型实际输出的误差达到设定值时,模型停止训练,获得训练好的弹药消耗量预测模型。 模型测试过程步骤为: 步骤1:获得弹药消耗量数据,对数据进行预处理,获得模型的测试过程输入数据; 步骤2:将测试过程输入数据输入到建立的弹药消耗量预测模型中进行测试; 步骤3:得出未来年份的弹药预测结果。 通过利用建立好的模型进行测试,可以获得下一年的弹药消耗量。与现有弹药储存情况进行比较,可以有效地分析出该类弹药的需求情况。通过上述方法,可以对弹药供应保障的消耗量需求进行有效预测,为弹药供应保障的统筹规划和合理安排提供参考。 通过前述内容的描述与分析可知,BP神经网络方法可以较好地对弹药的消耗量进行预测,并能间接反映出高寒山地的弹药供应保障情况。这里,以某高寒山地的某种弹药消耗量的数据为例(此数据为模拟数据,在实际数据的基础上有改动),通过建立BP神经网络预测模型对该地区弹药供应保障需求进行分析。 3.1模型数据的获取与预处理 以该高寒山地1996—2013年的弹药消耗量为例,表1和图3显示了该地区每年的弹药消耗量情况。 图2 弹药消耗量预测模型流程 时间/年199619971998199920002001200220032004弹药消耗量/t408502573702786994129114081590时间/年200520062007200820092010201120122013弹药消耗量/t180619972062205221112169225023592714 从图3中可以看出,该高寒山地每年弹药的消耗量成逐年递增的趋势。为了进一步探究该高寒山地2014年弹药的消耗量,利用BP神经网络对其建立预测模型。 图3 某高寒山地的弹药消耗量 本文中,设置s=3,则第一个输入样本为p1=[408,502,573]T,第一个输出样本为 t1=702;第二个输入样本为p2=[502,573,702]T,第二个输出样本为 t2=786,依次得到15组输入样本和输出样本数据。将这些一一对应的输入、输出数据作为BP神经网络模型的训练数据。模型预测时,利用最近3年的弹药消耗量构造输入样本,表示为ptest=[2250,2359,2714]T,将其作为测试数据进行模型预测。 3.2模型结构的确定 为了提高网络的训练速度,选取只有一个隐含层的3层BP神经网络预测模型并对其进行训练。输入、输出变量具体对应相应的输入、输出层神经元,因此将输入层神经元个数设定为3,输出层神经元个数设定为1,并利用式(4)对隐含层神经元的个数进行确定,这里,设定隐含层神经元个数为10。此时BP神经网络的结构为3-10-1,即输入层、隐含层和输出层的神经元个数分别为3、10、l。此外,设置隐含层的神经元和输出层的神经元激活函数分别为tansig函数和线性函数。 对于模型训练参数,设定网络最大学习迭代次数为1 000,训练速率为0.05,训练目标误差为0.0015。 3.3模型训练与测试 以该高寒山地某种弹药消耗量为例,利用Matlab工具对BP神经网络模型进行训练与测试。图4和图5给出了BP神经网络模型训练过程和训练后的结果。从其中可以看出,当BP网络迭代到640次时,训练误差达到了设定值,此时模型停止训练。测试时,将测试数据 ptest=[2 250, 2 359, 2 714]T输入到训练好的模型中,即可预测得出2014年该高寒山地的弹药消耗量。利用2014年的弹药预测消耗量构造新的测试数据,将其作为模型输入进行测试,即可得出2015年该高寒山地的弹药消耗量,依次类推。 图4 BP神经网络训练 图5 BP神经网络的误差迭代 3.4弹药消耗需求的预测结果 将训练数据中的输入量代入训练好的BP神经网络模型中,即可得出1996—2013年的弹药预测消耗量。图6给出了相应的预测结果:圆圈代表弹药真实消耗量,*号代表弹药预测消耗量。可以看出两条曲线基本重合,说明BP神经网络模型预测值与真实值之间的误差非常小,其建立的模型具有较高的精度。利用训练好的模型预测得到2014—2015年的弹药消耗量分别为2 663t和3 179t。以下给出了弹药消耗量预测模型的BP神经网络核心程序。 图6 BP神经网络测试结果 可以看出,利用BP神经网络得到的弹药预测消耗量曲线与弹药真实消耗量曲线比较接近,表明了所建立的弹药供应保障消耗量需求模型能够很好地预测弹药消耗量。 结合战场的实际作战环境以及各兵种的投入情况,科学合理地对弹药消耗量的需求进行分析和评估,尤其是高寒山地条件下弹药消耗量的准确预计是目前我军在装备供应保障过程中亟需解决的问题。本文在相关研究的基础上,以某高寒山地的某种弹药消耗量的实际情况为例,通过建立BP神经网络预测模型对该地区弹药供应保障需求进行了分析。结果表明,利用BP神经网络得到的弹药预测消耗量曲线与弹药真实消耗量曲线比较接近,所建立的弹药供应保障消耗量需求模型能够很好地预测弹药消耗量。 参考文献: [1]WILLIAMF.StudyofAmmunitionconsumption(AD-A451782)[R].Washington,D.C.,2005. [2]AKST,GEORGE.MarineCorpsReserveMunitionsRequirement(WRMR)ModelVersion2.3,Accreditation[R].[S.l.]:[s.n.],2007. [3]DIAZA.HeuristicsGlobalCombatLogisticsForceOperationalPlanning[D].USA:NavalPostgraduateSchool,2010. [4]RAJASHEREKF,PAKKALATPM.ABayesianapproachtoadynamicinventorymethodunderanunknowndemanddistribution[J].ComputerandOperationsResearch,2002(29):403-422. [5]KOSTAS-PLATONARONIS,LOULIAMAGOU,ROMMERTDEKKER,etal.InventorycontrolofsparepartsusingaBayesianapproach:acasestudy[J].EuropeanJournalofOperationalresearch,2004(154):730-739. [6]荣鹏辉,陆廷金,许栩.基于AHP的弹药存储需求量模型优化研究[J].弹箭与制导学报,2006,26(3):12-14. [7]俞杰,王三喜,沈寿林,等.基于SD模型的弹药消耗规律研究[J].火力与指挥控制,2008,33(4):26-27. [8]王三喜.联合火力打击弹药需求计算动态模型研究[J].火力与指挥控制,2009,34(10):100-102,107. [9]黄天辰.基于神经网络的弹药消耗预测[J].军械工程学院学报,2004,16(2):29-41. [10]朱培涛.弹药消耗预测方法比较研究[J].兵工自动化,2007,26(4):L2. [11]陈基纯,王枫.房地产价格时间序列预测的BP神经网络方法[J].统计与策略,2008(14):42-43. [12]戴革林.基于BP算法和单目标供给的航空弹药需求仿真[J].计算机仿真,2007,24(2):15-17. (责任编辑唐定国) doi:10.11809/scbgxb2016.06.023 收稿日期:2015-11-25;修回日期:2015-12-30 作者简介:齐浩淳(1984—),男,工学博士,工程师,主要从事军械装备保障技术、雷达装备、无人机、可靠性研究等研究。 中图分类号:E932 文献标识码:A 文章编号:2096-2304(2016)06-0097-05 DemandAnalysesofAmmunitionConsumptioninColdMountainAreasBasedonBPNeuralNetwork QIHao-chun1,HUANGDa-peng2,WEIJiu-nan1,CHENZhi-gang1 (1.TheNo. 68129thTroopofPLA,Lanzhou730060,China; 2.OrdnanceEngineeringCollegeofPLA,Shijiazhuang050030,China) Abstract:Using BP neural network method, the paper established the prediction model of ammunition consumption in the cold mountain areas, and described its forecasting processes and procedures. Combined with the cold mountain areas’ realities, the paper also analyzed their consumption demands of ammunition supply support. Finally, the forecast results show that the model can well predict the ammunition consumption in the cold mountain areas. Key words:cold mountain area; ammunition consumption; BP neural network2 弹药消耗预测模型
3 弹药消耗量需求分析的应用





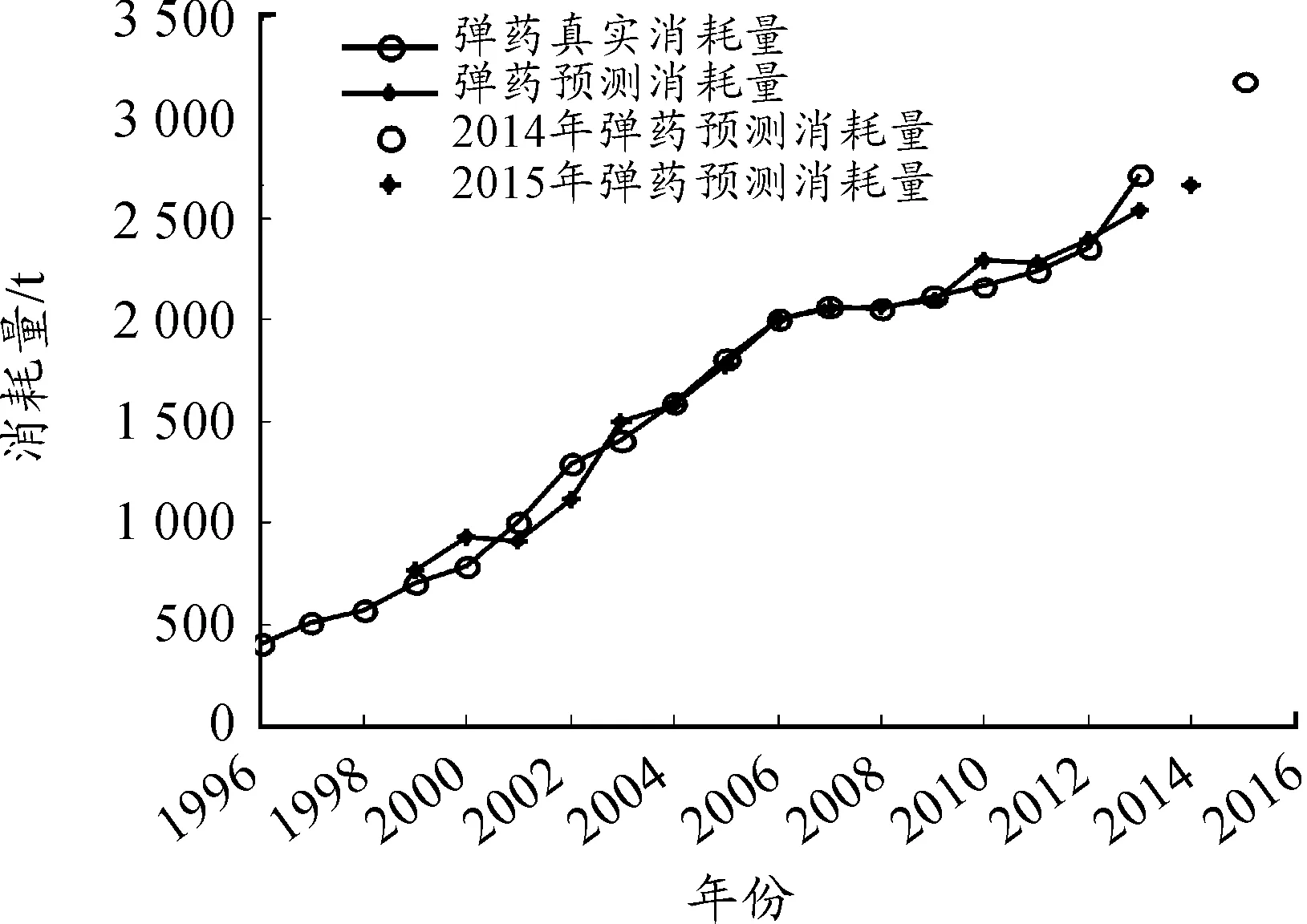
4 结论
