基于Markov方法的多阶段任务系统可靠性分析综述

闫　华，王　魁，刘子林，付前峰

(1.后勤工程学院　a.后勤信息与军事物流工程系； b.科研部, 重庆　401311； 2. 77416部队, 重庆　400054)



基于Markov方法的多阶段任务系统可靠性分析综述

闫华1a，王魁1b，刘子林1a，付前峰2

(1.后勤工程学院a.后勤信息与军事物流工程系；b.科研部, 重庆401311； 2. 77416部队, 重庆400054)

摘要：基于Markov方法的PMS任务可靠性建模方法大致可以分为统一建模、分阶段建模、层次化建模以及模块化建模，介绍了各种建模方法的主要思路及优缺点;同时，分析总结了基于Markov的任务可靠性模型求解方法，并指出大规模PMS的Markov可靠性建模与分析方法是下一步需要研究解决的问题。

关键词：多阶段任务系统；任务可靠性；Markov过程

本文引用格式：闫华，王魁，刘子林，等.基于Markov方法的多阶段任务系统可靠性分析综述[J].兵器装备工程学报，2016(6):92-96.

Citationformat:YANHua,WANGKui,LIUZi-lin,etal.ReliabilityAnalysisofPhased-MissionSystemUsingMarkovApproach[J].JournalofOrdnanceEquipmentEngineering,2016(6):92-96.

随着现代系统变得越来越复杂和智能化，系统的运行不再是单一过程，而是包括了多个功能流程的转换，或者在不同阶段通过对单元重组形成新系统的过程，这样的系统称之为多阶段任务系统(phased-missionsystem,PMS)。PMS经常被配置到关键应用中，特别是航天和军用装备领域[1]，如巡航导弹系统[2]，防空武器系统[3]及航天测控系统[4]等，这些系统中对于任务可靠性都具有很高的要求。同时，PMS任务可靠性分析对于发现系统薄弱环节、改进设计、合理分配可靠性指标等都具有重要的作用。因此，基于PMS的可靠性建模与分析也逐渐成为研究的热点。

根据很多文献的论述[5-8]，PMS具有以下3个特点：系统功能的实现依赖于多个阶段性子任务；系统配置、任务成败标准和单元失效率等随时间发生变化；各阶段时间连续且不重叠。因此，PMS可以概括为：系统功能的实现包括多个时间连续且不重叠的阶段，系统配置、任务成败标准及单元参数等可能随阶段发生变化。

1　PMS可靠性分析方法概述

PMS任务可靠性建模与分析方法大致可分为以下3类：组合模型法，基于状态空间的方法和系统仿真法。

1) 组合模型法：包括可靠性框图法和故障树方法。组合模型法具有简洁直观的特点，但只适合对静态PMS建模，对于单元可修复以及阶段转换时间随机的PMS等动态系统无法进行分析。

① 可靠性框图法：可靠性框图是根据系统的功能图(或称原理图)，再考虑组成系统的各单元对系统功能的影响而得到的逻辑关系图。以航天测控任务为例，图1描述了该任务中各测控站点的执行时序图，各阶段的可靠性框图如图2所示。

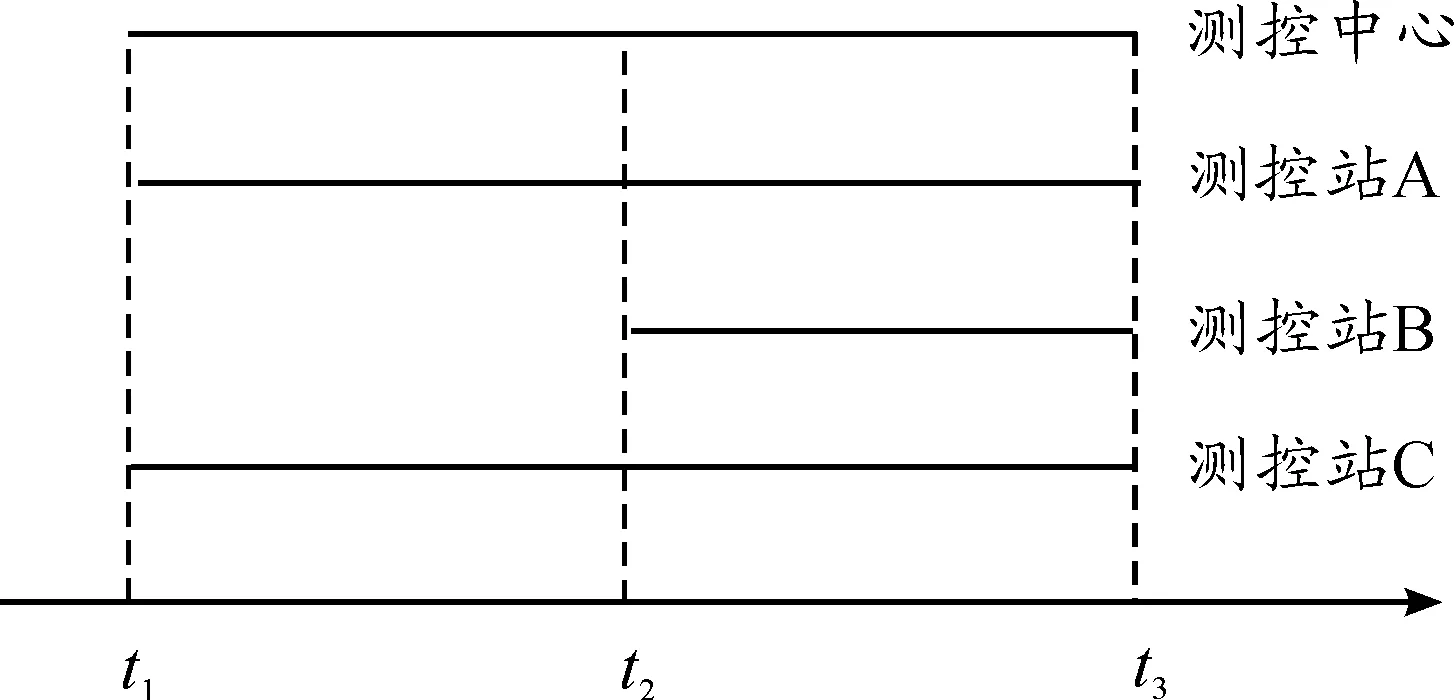
图1　航天测控任务的执行时序

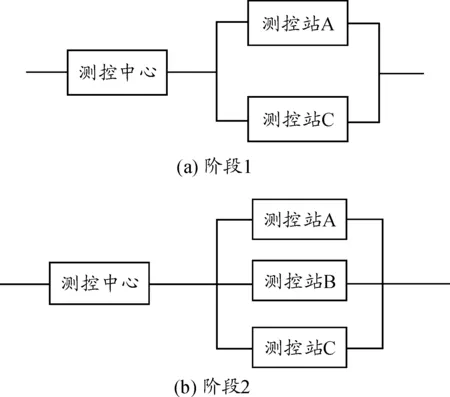
图2　测控任务各阶段可靠性框图

关于可靠性框图的求解，最简单的方法是将每个阶段的框图依次串联起来，然后对合并后的模型进行求解，这种方法得到的系统可靠性是保守值。因为在该方法中，某一阶段中的事件会对后续的所有阶段都产生影响。还有一种部件分解法，将每个阶段内的部件分解为一系列统计独立的小部件，从而消除阶段间的相关性。然而，随着系统规模的增大，部件分解法的复杂性呈指数增长。

② 故障树法：故障树法把系统最不希望发生的故障状态作为故障分析的目标，把选定的系统故障状态称为顶端事件，然后由顶端事件依次向下分析，找出造成当前节点事件发生的直接因素，一直追溯到那些原始的或其故障机理或概率分布都是已知的、不需继续分析的因素为止。以图1中的测控任务为例，其各阶段故障树如图3所示。

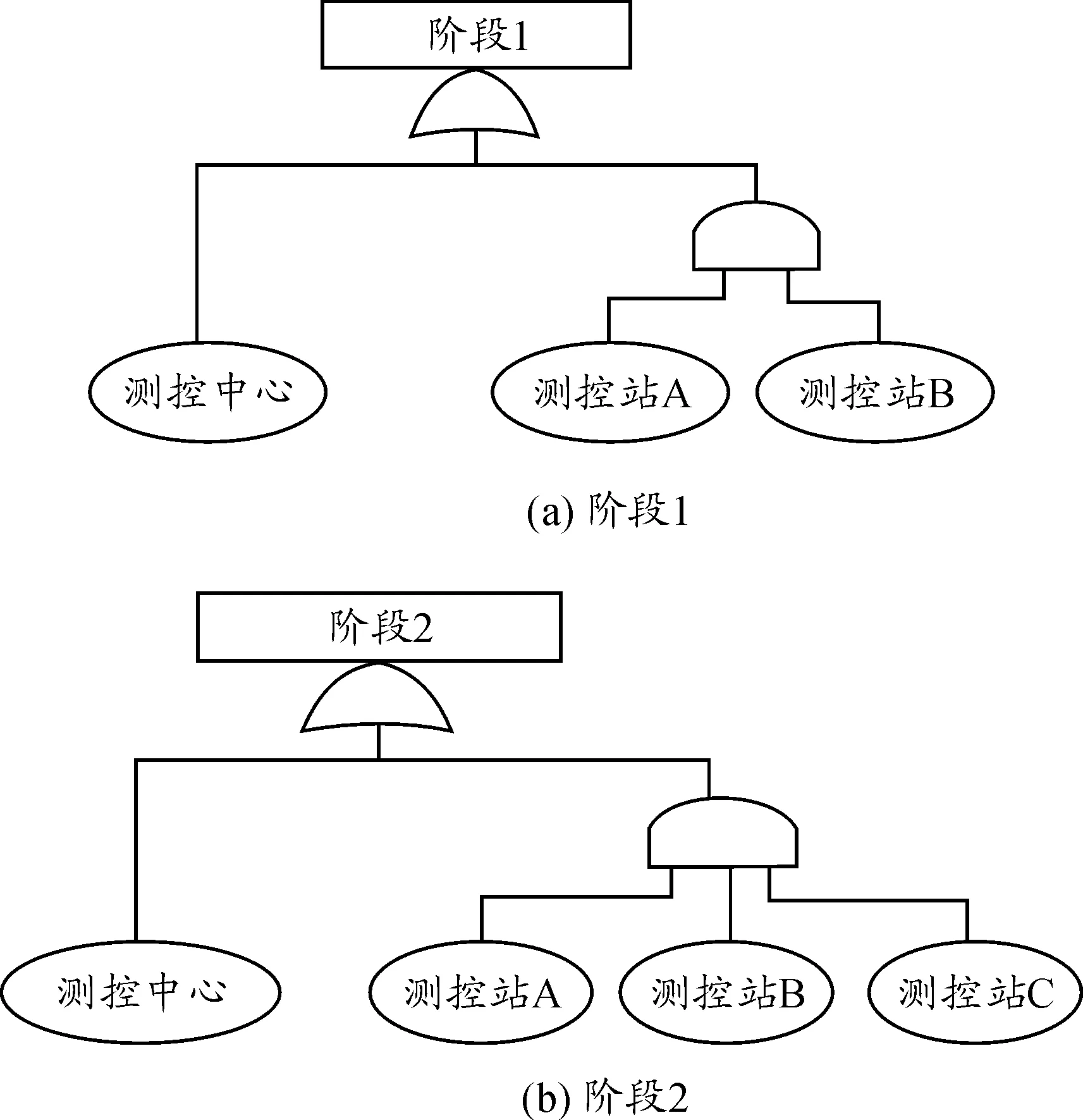
图3　测控任务各阶段故障树模型

利用故障树可以描述PMS的可靠性需求，其建模过程与可靠性框图法类似，也是首先构造各个任务阶段的故障树模型，然后将当前阶段的模块用若干串联形式的前面阶段的同一单元模块置换，得到等价的故障树模型，传统的故障树方法无法处理动态系统。故障树模型的分析方法包括部件分解法、割集计算法以及基于二元决策图(BinaryDecisionDiagram，BDD)[9-10]方法，其中BDD方法的求解效率最高。

2) 基于状态空间的方法：包括Markov方法和Petri网方法，都是基于随机过程的理论进行分析。Petri网在PMS可靠性方面的研究包括Mura等[11-12]提出的基于Petri网的PMS可靠性分析模型，开发的基于Petri网方法的建模工具DEEP[13-14]，为PMS的可靠性分析提供了功能强大的集成环境；Wu等[15]基于扩展的面向对象Petri网，建立了能够处理共因失效和部件修复的任务可靠性模型。相比组合模型法，状态空间方法在建模能力方面具有很高的灵活性，但是，这种灵活性和通用性的统一需要一定的代价，伴随而来建模方法和模型处理的更高复杂性。

3) 系统仿真法：系统仿真法适用于任何情况，但计算工作量大是其在应用过程中的主要瓶颈。Murphy等[16]开发的Raptor仿真工具可完成对PMS可靠性仿真，但该工具所使用的仿真方法属于粗仿真，因此仿真效率较低。Xu等[17]提出了基于强制法和失效偏移的PMS任务可靠性仿真方法，但该方法适用于具有大量冗余部件和较短任务时间的系统。

另外，GO方法也是一种重要的可靠性评估方法，适用于有多重状态、时序变化复杂系统的可靠性分析[18]。钟小军等[19]建立了基于GO法的多阶段共因失效任务可靠性模型，为PMS任务可靠性评估提供了新的研究思路。

2　基于Markov过程的任务可靠性建模

基于Markov过程的可靠性分析方法一般假设组成系统的各单元寿命分布以及维修分布均服从指数分布，通过建立系统的Markov模型，分析微观状态的转移过程并得到系统可靠性。该方法的优点是能够处理动态可修系统的可靠性分析，同时对于多阶段任务系统，能够正确描述阶段内各部件之间的依赖性以及部件跨阶段的依赖性。以图1所示测控任务为例，分别建立两个阶段的Markov模型，其状态转移过程如图4所示。

从20世纪70年代以来，国内外学者经过多年的研究，已提出了许多基于Markov过程的的PMS可靠性建模方法，大致可以分为以下4类：统一建模方法；分阶段建模方法；层次建模方法；模块化建模方法。

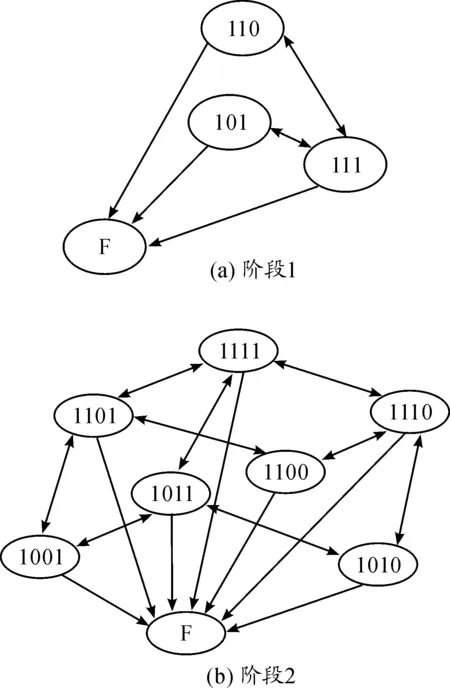
图4　测控任务各阶段Markov模型状态转移过程

2.1统一建模方法

统一建模是指将系统各阶段模型综合起来，建立统一的Markov可靠性模型。Smotherman等[20]运用非齐次Markov模型直接构建系统所有各个阶段的CTMC可靠性模型。Dugan[21]提出了一种利用各阶段故障树自动转换生成统一Markov模型的方法。

统一建模的优点是模型单一，过程简单，不需要进行阶段间状态匹配；缺点是模型建立困难，同时最终模型中的状态空间较大，因此模型求解困难。

2.2分阶段建模方法

分阶段建模是指将PMS中多个连续的阶段分别看作单阶段系统建立可靠性模型，并以前一阶段末系统处于各状态的概率作为下一阶段系统的初态，逐阶段进行系统的任务可靠性分析。Alam[6]和Somani[22]等都采用分阶段建模方法建立PMS系统的任务可靠性模型并进行求解，Somani同时开发了相应的软件包。

与统一建模方法相比，分阶段建模由于每次只处理单个阶段，建模过程较为简单且单阶段模型通常都小于统一模型；缺点是需要处理阶段间状态映射机制，由于分阶段处理时，不同阶段中参与任务的设备及其数量通常会发生变化，导致两个阶段的状态概率向量不能直接匹配，特别是当系统规模较大时，阶段间状态映射较为复杂。闫华等[23]研究了阶段间状态映射的基本规则，提出了不同情况下的状态映射机制。

2.3层次化建模方法

由于Markov模型存在状态空间爆炸问题，为了减少状态空间数量、提高模型求解效率，目前很多文献的研究思路是将组合模型法和Markov法结合起来，主要有层次化建模方法[24-26]和模块化建模方法[27]。

层次化建模方法是指将PMS分为顶层系统级和底层单元级，顶层系统用组合模型描述，底层微观状态由Markov模型描述。基于Zang和Sun等[9]的BDD模型，Wang和Trivedi[24]研究了在部件可修复情况下多阶段系统可靠性的分层建模方法，利用BDD方法表示系统级结构函数并进行求解，底层单元级的故障/修复等动态过程利用CTMC建立模型。BDD方法在表示布尔函数方面具有简洁、高效等优势。

2.4模块化建模方法

模块化建模方法是指将系统划分为静态模块和动态模块，静态模块由组合建模法分析，动态模块利用Markov法进行分析。Ou和Dugan[27]提出了一种模块化分析PMS任务可靠性的方法，对系统中的静态模块和动态模块分别建立模型，将不同模块的计算结果利用模块联合概率(ModuleJointProbability)方法进行综合，并最终得到系统的任务可靠性；陈光宇等[28]针对通用PMS，提出了基于模块化思想的分离BDD方法，实现了不完全覆盖条件下系统可靠性建模的简化和高效计算。

混合类方法的效果主要依赖于PMS中动态成分的比重，当动态成分规模较大时，依然存在建模与分析计算的时空复杂性问题。因此，如何减少动态成分的规模是十分关键的问题。

3　Markov可靠性模型求解算法

利用Markov模型求解航天测控通信系统任务可靠性，主要是计算t时刻系统的状态概率向量v(t)，根据Chapman-Kolmogorov微分方程，有以下公式：

(1)

其中矩阵Q为Markov模型的转移速率矩阵(或无穷小生成子)。

式(1)中的形如eA的表达式被称为矩阵指数函数(matrixexponentialfunction)，矩阵指数函数eA的计算方法很多[29]。Moler[30]对现有的矩阵指数计算方法进行了大致总结，主要包括Taylor展开方法、Pade方法、比例与平方方法、常微分方法和矩阵分解方法等。

Moler指出上述方法并不存在一种在所有情况下都能高效求解的算法，这些方法主要针对中小型矩阵，矩阵阶数不大于几百，大部分方法都不适合大型稀疏矩阵的求解。因为上述方法中包括大量的矩阵幂运算，其缺点是若初始矩阵为稀疏矩阵，经过幂运算后其稀疏性逐渐消失，导致计算效率低下。

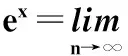
4　结论

现有的PMS任务可靠性分析方法主要有BDD方法、仿真方法和Markov方法。其中，Markov方法能够处理可修系统，且理论上可以求得精确解，满足对航天测控系统等关键领域高精度计算要求。但是，从现有文献看，对于大规模复杂PMS，采用基于Markov的可靠性建模与求解方法，从理论及实现手段上都难以满足要求。因此，对基于Markov过程的大规模PMS任务可靠性建模与求解方法进行研究，建立合理的简化模型、提出高效的模型求解算法，不仅在基础理论上有重要价值，而且在今后的实际应用中也具有重要意义。

参考文献：

[1]LIL,QIANY,YANGY.EvaluatingMissionReliabilityforComplexWeaponSystemswithProbabilisticModelChecking[J].JournalofMechanicalEngineering, 2011, 47(24):171-175.

[2]刑涛.多阶段任务可靠性建模研究[J].海军航空工程学院学报, 2006, 21(1):172-174.

[3]LIUB.MissionReliabilityAnalysisofMissileDefenseSystemBasedonDODAFandBayesianNetworks[C]//Proceedingsof2011InternationalConferenceonQuality,Reliability,Risk,Maintenance,andSafetyEngineering,ChinaXi’an: 2011:777-780.

[4] 许双伟, 武小悦.航天测控任务可靠性的混合分析方法[J].系统工程与电子技术, 2013, 35(3):667-671.

[5]ESARYJD,ZIEHMSH.ReliabilityAnalysisofPhasedMissions[C]//ProceedingsoftheConferenceonReliabilityandFaultTreeAnalysis.Philadelphia,USA:SIAM,1975: 213-236.

[6]ALAMM,AL-SAGGAFUM.QuantitativeReliabilityEvaluationofRepairablePhased-MissionSystemsUsingMarkovApproach[J].IEEETransactionsonReliability, 1986,R-35(5):498-503.

[7]ALAMM,SONGM,HESTERSL,etal.ReliabilityAnalysisofPhased-MissionSystems:APracticalApproach[C]//Proceedings-AnnualReliabilityandMaintainabilitySymposium.NewportBeach,CA,Unitedstates:InstituteofElectricalandElectronicsEngineersInc.,2006: 551-558.

[8]YANGC,YANGJ,BIANJ.ThePMSmodelingmethodbasedoninteractiveMarkovchain[C]//The9thConferenceonReliability,MaintainabilityandSafety(ICRMS).Guiyang:IEEE,2011: 349-352.

[9]ZANGX,SUNH,TRIVEDIKS.ABDD-BasedAlgorithmforReliabilityAnalysisofPhased-MissionSystems[J].IEEETransactionsonReliability, 1999, 48(1):50-60.

[10]XINGL,LEVITING.BDD-BasedReliabilityEvaluationofPhased-MissionSystemswithInternal/ExternalCommon-CauseFailures[J].ReliabilityEngineering&SystemSafety, 2013, 112(1):145-153.

[11]MURAI,BONDAVALLIA,ZANGX,etal.DependabilityModelingandEvaluationofPhasedMissionSystems:ADSPNApproach[C]//Proceedingofthe7thIFIPInternationalConferenceonDependableComputingforCriticalApplications.SanJose,California,USA,1999: 319-337.

[12]MURAI,BONDAVALLIA.MarkovRegenerativeStochasticPetriNetstoModelandEvaluatePhasedMissionSystemsDependability[J].IEEETransactionsonReliability, 2001, 50(12):1337-1351.

[13]BONDAVALLIA,CHIARADONNAS,GIANDOMENICOFD,etal.DependabilityModelingandEvaluationofMultiple-PhasedSystemsUsingDEEM[J].IEEETransactionsonReliability, 2004, 53(4):509-522.

[14]BONDAVALLIA,MURAI,CHIADRADONNAS,etal.DEEM:AToolfortheDependabilityModelingandEvaluationofMultiplePhasedSystems[C]//ProceedingoftheInternationalConferenceonDependableSystemsandNetworks.NewYork,UnitedStates,2000: 231-236.

[15]WUX,WUX.ExtendedObject-OrientPetriNetModelforMissionReliabilitySimulationofRepairablePMSwithCommonCauseFailures[J].ReliabilityEngineering&SystemSafety, 2015, 136(7):109-119.

[16]MURPHYKE,CARTERCM,MALERICHAW.Reliabilityanalysisofphased-missionsystems:ACorrectApproach[C]//Proceedings-AnnualReliabilityandMaintainabilitySymposium.Orlando,FL,Unitedstates,2007: 7-12.

[17]XUS,WUX.SimulationMethodforReliabilityofTT&CMissionwithHighRedundancyandSmallTimeHorizon[J].JournalofSystemsEngineeringandElectronics, 2012, 23(6):943-948.

[18]尹宗润, 李俊山, 苏东.基于Bayes-GO的复杂系统可靠性评估模型[J].计算机工程, 2013, 39(11):276-279.

[19]钟小军, 陈辰, 杨建军.基于GO法的多阶段共因失效任务系统可靠性评估[J].海军工程大学学报, 2012, 24(4): 86-90.

[20]SMOTHERMANM,ZEMOUDEHK.ANon-HomogeneousMarkovModelforPhased-MissionReliabilityAnalysis[J].IEEETransactionsonReliability, 1989, 38(5): 585-590.

[21]DUGANJB.AutomatedAnalysisofPhased-MissionReliability[J].IEEETransactionsonReliability, 1991, 40(1): 45-52.

[22]SOMANIA,RITCEYJ,AUS.Computationally-EfficientPhased-MissionReliabilityAnalysisforSystemswithVariableConfigurations[J].IEEETransactionsonReliability, 1992, 41(4): 504-511.

[23]闫华, 武小悦.多阶段系统可靠性分析的状态映射机制[C]//2011年复杂系统理论与方法及其工程实践学术会议论文集.北京: 中国系统工程学会,2011: 648-651.

[24]WANGD,TRIVEDIKS.ReliabilityAnalysisofPhased-MissionSystemwithIndependentComponentRepairs[J].IEEETransactionsonReliability, 2007, 56(3): 540-551.

[25]SHRESTHAA,XINGL,DAIY.ReliabilityAnalysisofMulti-StatePhased-MissionSystems[C]//ReliabilityandMaintainabilitySymposium.FortWorth,TX,Unitedstates:InstituteofElectricalandElectronicsEngineersInc.,2009: 151-156.

[26]LUJ,WUX.ReliabilityEvaluationofGeneralizedPhased-MissionSystemswithRepairableComponents[J].ReliabilityEngineering&SystemSafety, 2014,121(5):136-145.

[27]OUY,DUGANJB.ModularSolutionofDynamicMulti-PhaseSystems[J].IEEETransactionsonReliability, 2004, 53(4): 499-508.

[28]陈光宇, 张小民, 唐小我.基于分离BDD的通用多阶段任务系统可靠性分析[J].系统工程理论与实践, 2013, 33(5): 1240-1246.

[29]STEWARTWJ.IntroductionoftheNumericalSolutionofMarkovChains[M].Princeton,NJ:PrincetonUniversityPress, 1994.

[30]MOLERC,LOANCV.NineteenDubiousWaystoComputetheExponentialofaMatrix,Twenty-FiveYearsLater[J].SIAMReview, 2003, 45(1):3-49.

[31]ROSSSM.IntroductiontoProbabilityModels[M].AcademicPress, 2006.

[32]REIBMANA.NumericalTransientAnalysisofMarkovModels[J].ComputersAndOperationResearch, 1998, 15(1): 19-36.

[33]RAUZYA.AnExperimentalStudyonIterativeMethodstoComputeTransientSolutionsofLargeMarkovModels[J].ReliabilityEngineering&SystemSafety, 2004, 86(1): 105-115.

[34]钟万勰.结构动力方程的精细时程积分[J].大连理工大学学报, 1994, 34(2): 131-136.

[35]张洪武, 钟万勰.矩阵指数计算算法讨论[J].大连理工大学学报, 2000, 40(5): 522-525.

[36]闫华, 武小悦.航天测控通信系统可靠性分析的Krylov子空间投影算法[J].国防科技大学学报, 2012, 34(4): 63-67.

(责任编辑唐定国)

doi:【后勤保障与装备管理】10.11809/scbgxb2016.06.022

收稿日期：2015-11-30；修回日期：2015-12-30

基金项目：国家自然科学基金项目(71401172)

作者简介：闫华(1983—)，男，博士，讲师，主要从事系统可靠性建模与分析研究。

中图分类号：TP202.1

文献标识码：A

文章编号：2096-2304(2016)06-0092-05

ReliabilityAnalysisofPhased-MissionSystemUsingMarkovApproach

YANHua1a,WANGKui1b,LIUZi-lin1a,FUQian-feng2

(1.a.DepartmentofLogisticsInformation&LogisticsEngineering;b.DepartmentofScientificResearch,LogisticEngineeringUniversity,Chongqing401311,China; 2.TheNo. 77416thTroopofPLA,Chongqing400054,China)

Abstract:The modeling methods based on Markov process of PMS mission reliability can be divided into four categories: unified modeling method, separate modeling method, hierarchical modeling method and modular modeling method. The main ideas, advantages and disadvantages of above modeling methods were introduced. Also, the mission reliability computing methods for Markov model were analyzed. On the basis of the latest research advance, the reliability modeling and analysis methods of large-scale PMS based on Markov process was pointed as an important issue in the future.

Key words:phased-mission system; mission reliability; Markov process