基于概率论的直升机使用飞行谱编制
2016-08-12杨华高
罗 航,杨华高,江 煜
(海军驻景德镇地区航空军事代表室,江西 景德镇 333002)
基于概率论的直升机使用飞行谱编制
罗航,杨华高,江煜
(海军驻景德镇地区航空军事代表室,江西 景德镇333002)
摘要:通过对国外某型直升机典型飞行科目中的时间、起落次数等信息的分析,进行了基于概率论的直升机飞行谱编制方法设计,并用该方法编制了直升机使用飞行谱,经验证该方法能较真实地反映该型直升机的使用情况,在使用寿命估计方面有较高的计算精度。
关键词:直升机;飞行谱;概率论
本文引用格式:罗航,杨华高,江煜.基于概率论的直升机使用飞行谱编制[J].兵器装备工程学报,2016(6):39-44.
Citationformat:LUOHang,YANGHua-gao,JIANGYu.CompilingoftheHelicopterUsingFlightSpectrumBasedonProbabilityTheory[J].JournalofOrdnanceEquipmentEngineering,2016(6):39-44.
21世纪是海洋世纪, 海空一体化建设的不断完善,需要越来越多的直升机来执行反潜、运输、通信、巡逻、救护、护航、联合军演等多样化军事任务,与之相关的直升机维修保障能力也亟待不断提升。当前,国内直升机损伤分析和状态监控主要是靠设计飞行谱,而不是反映真实情况的使用飞行谱,在结构安全评估和延寿等方面分析效果不佳。由于直升机机动灵活,飞行状态多变,随机性强,其使用飞行谱必须在大量飞行使用数据统计的基础上,通过数理统计分析后才具有有效性和可行性。
直升机飞行谱,是直升机使用方法的函数,是飞行载荷实测、载荷谱编制以及直升机定寿的基本依据之一。实际的飞行谱反映了整个直升机机群和单架机的平均使用情况。基于飞行谱,通过计算,可以定量考察不同的飞行状态对直升机相关动部件造成的疲劳损伤。进一步通过累计损伤计算,可以将直升机动部件的性能量化,为整个机群和单机进行损伤分析和状况监控、合理安排飞行任务、确定重点检查和维修部位提供参考。
由于国外直升机技术发展较为成熟,其使用飞行谱编制方法也较为完善,但由于涉及到知识产权保护、技术限制和军用装备保密等问题,国内难以获得较具体的技术与资料, 因此,本文以国外某型直升机实际飞行数据为基础,开展了基于概率论的直升机使用飞行谱编制方法研究。
1 飞行数据统计分析
1.1飞行科目统计分析
根据查阅该型直升机资料,可得部分飞行科目是为编队飞行、编队带飞、超低空空域飞行、超低空空域带飞等,单飞和带飞的飞行剖面是相同的,类似上述类型的科目,可以合并。气象飞行科目如海上悬停飞行、夜间海上悬停飞行等科目的飞行剖面的构成是基本相同或十分相近的,一次飞行所需时间也相同,此类科目同样进行合并。考虑上述归并原则,可确定该直升机飞行科目合并成27个,由于篇幅所限,这里不予列出。
1.2飞行状态统计分析
飞行科目的飞行任务剖面各不相同,分别由不同的飞行状态组成,且各飞行状态在每个飞行科目中所占的时间比例不同。通过对全部飞行科目的分析,对27个典型科目按飞行状态进行分解,共得到51个不同的典型飞行状态,如垂直起飞、滑跑起飞、左侧飞、右侧飞等。
1.3飞行谱样本数据统计
直升机飞行谱样本数据的统计处理过程分为两个步骤,一是确定典型飞行状态在各典型飞行科目中所占的时间百分比;二是确定各个典型飞行科目的统计飞行时间和起落次数。具体过程如下:
1) 确定典型飞行科目中典型飞行状态所占的时间百分比。典型飞行科目的飞行时间,可由该飞行科目中所含飞行状态的持续时间求和计算,表示为
(1)
式(1)中:Ti为第i个典型飞行科目的一次飞行时间,ti(sj)为第i个典型飞行科目第j个典型飞行状态sj的持续时间。于是,各飞行状态占该科目的飞行时间百分比表示为
(2)
式(2)中:vi,j为第i个典型飞行科目第j个典型飞行状态sj的时间百分比。
合理确定典型科目中各飞行状态的持续飞行时间是飞行谱编制的关键。经统计分析得到典型科目中各个飞行状态所占用的均值时间百分比,同时对该比值采取抽样方法与飞参记录的该状态飞行时间比进行检验确认。该直升机飞行员母体完成27种典型科目中51个飞行状态所占用的时间比,如图1所示。
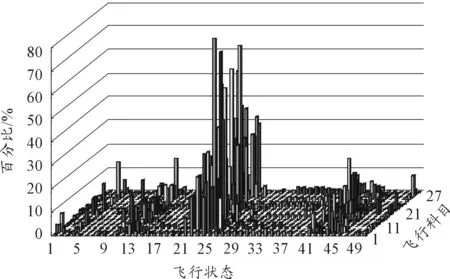
图1 典型飞行科目中各典型飞行状态所占的时间百分比
2) 确定各个典型飞行科目的统计飞行时间和起落次数。查阅资料得到各架机对应27个典型飞行科目的飞行时间和起落次数。在对每次飞行进行数据统计时,应尽可能考虑飞行物理参数如飞行质量、重心位置、飞行高度、大气温度。
3) 确定使用飞行谱样本数据。采用“单机-累年”统计方法,根据27个典型飞行科目中51个典型飞行状态所占的时间百分比构成,以单机为基本统计单元,以各单机的27个典型飞行科目的总飞行时间为权重,确定各单机累年飞行中各典型飞行状态所占的时间百分比,也即飞行谱样本,表示为
(3)
式(3)中:vj为飞行谱样本中第j个飞行状态所占时间百分比;Ti为第i飞行科目的总飞行时间。图2所示为该直升机飞行谱样本。

图2 某直升机飞行谱样本
2 飞行谱样本的分析设计
2.1统计的中位秩和非参数置信区间
设t1,t2,…,tn(t1≤t2≤…≤tn)是一个来自概率分布函数为F(ti,λ1,λ2,…,λn)的母体的有序随机样本,其中,λ1,λ2,…,λn为分布参数。令
(4)
则可称Pi为该母体中个体小于第i个有序观测值ti的百分率。由于ti的值随着样本的不同而不同,所以,Pi的值也随着样本的变化而变化,所以Pi也是一个随机变量(随机变量用黑体字母表示),被称为第i个秩统计量,它的概率密度函数可表示为
(5)
如果定义Pmi为
(6)
则分位数Pmi为第i个秩统计量的中位秩。
给定n,由式(6)计算Pmi,就是中位秩(i=1,2,…,n)。对于一组已知的按升序排列的随机变量数据xi(i=1,2,…,n),第i个数据的试验概率值P(xi)一般采用中位秩Pm(xi),其近似经验公式取为
(7)
式(7)计算结果与中位秩查表结果比较,一般满足小数点后3位精度要求。
如果定义Pui和Pli如下:
(8)
则Pui和Pli分别被称为对应于置信度为r(r≥50%)的非参数单侧置信上限和单侧置信下限,即
(9)
区间[Pli,Pui]被称为置信度为2r-1的非参数置信区间,即
(10)
由于秩分布是一个β分布,所以对式(14)进行变换,可得
(11)
为了便于应用,表1分别给出了对应于单侧置信度r=95%,样本大小为n≤10的Pui值。Pli值可由 式(12)换算得到:

(12)
2.2飞行谱中飞行状态数据处理方法
1) 假设各个飞行状态所占的时间百分比分布相互独立。实际上,若飞行谱中有m个飞行状态,各个飞行状态时间百分比为v1,v2,…,vi,…,vm,则有
(13)
这表明各个飞行状态百分比之间有一定的线性相关性,某一飞行状态百分比的改变,必然导致其他各个飞行状态百分比相应改变。与此同时,考虑到对应于某一特定的飞行科目或任务,若干个飞行状态百分比显著增加,而另几个飞行状态百分比将明显减少,甚至某几个飞行状态消失,这说明这些飞行状态之间或相关,或互斥,或独立。为简化计算过程,同时保证能达到要求的精度,假设各个飞行状态百分比分布相互独立。
2) 假设各个飞行状态所占的时间百分比均服从正态、对数正态、双参数Weibull和Gumbel(I型极大值)4种连续型概率分布规律,这4种分布规律具有较强的适用性,能够满足飞行状态数据在准确性、可靠性方面的统计处理要求。
3) 在上述假设前提下,对各飞行状态所占的时间百分比样本进行统计处理,得到的母体飞行状态百分比若不满足求和为100%的要求,则需要进行归一化处理。归一化公式为
(14)
2.3飞行谱中飞行状态数据统计分布规律研究
假设某型直升机机群的飞行状态时间百分比(为便于表述,选用v代替vi表示任意飞行状态百分比)分别服从以下分布:正态分布、对数正态分布、双参数Weibull分布和Gumbel(I型极大值)分布,以子样推断母体的分布,从中择优确定母体最佳分布形式。各分布的概率密度函数f(v)和累积分布函数F(v)。
采用最小二乘法进行线性回归分析,并得到各种统计分布函数参量的点估计值。对以上4种统计分布中的累积分布函数等式两边取对数,分别进行线性变换,得到各种分布规律的线性方程,如表2所示。
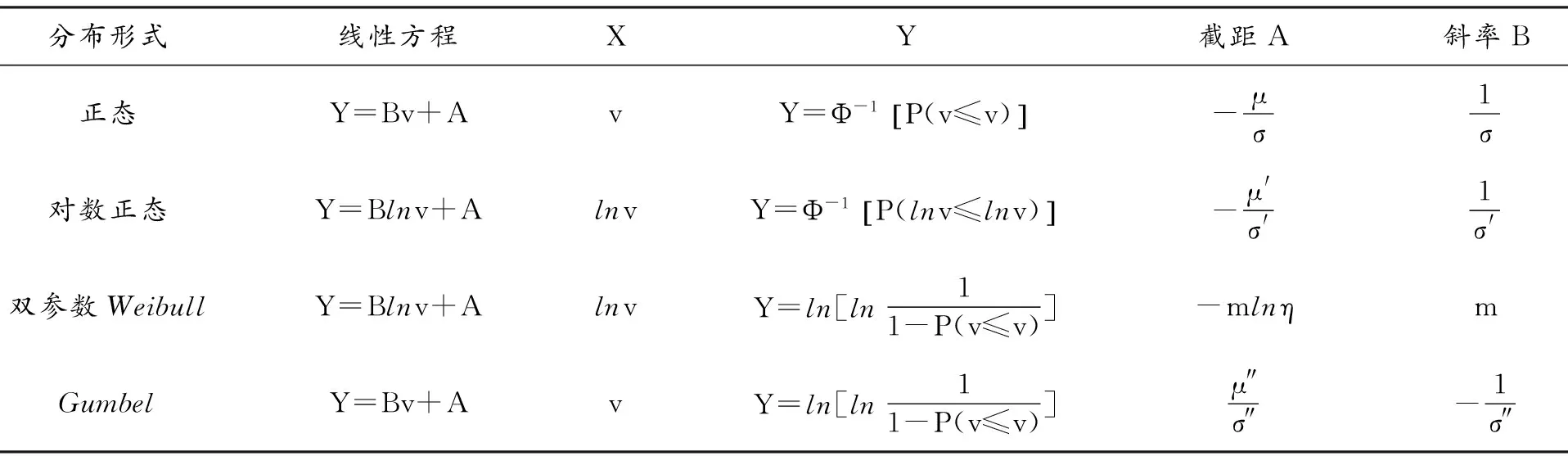
表2 各分布的线性回归方程
对所讨论的上述分布,可以用观察值代替理论值,并获得一组(Xi,Yi)数据。然后在对应的概率坐标图中采用最小二乘法对各分布进行拟合,计算得到其截距A、斜率B及相关系数R如下:
(15)
求得A、B值后,可根据表3,得到上述4种分布参数的估计值。
为了检验各数据点在对应的概率坐标图中是否线形相关,根据线性相关系数R与t分布的关系,可进行给定显著水平a下的统计检验。相关系数R与t分布的关系可表示为
(16)
式(16)中: tn-2表示自由度为n-2的t分布。根据式(24),在给定显著性水平a下满足假定分布函数的线性相关系数临界值Rc可表示为
(17)
当假设分布拟合数据的相关性系数R值大于临界值Rc时,则通过检验。
2.4飞行谱母体飞行状态数据统计检验与最佳估计
现以直升机“垂直起飞”飞行状态为例,进行母体统计推断分析,其样本数据见表4所示。
采用最小二乘法对假设的正态分布、对数正态分布、双参数Weibull分布和Gumbel分布分别进行线性回归分析、参数估计和统计检验。如垂直起飞状态各分布规律参数计算结果如表4所示。

表3 垂直起飞状态各分布规律参数计算结果

表4 垂直起飞和爬升状态母体推断统计样本数据
对4种分布类型的回归分析计算结果比较,如图3~图8所示。垂直起飞状态4种分布的线性相关性系数R值满足在显著性水平α=0.05时R>Rc,且R值均大于0.9。显然,垂直起飞状态的4种分布拟合均为高度线性相关,且以Gumbel分布相关性最高,故取垂直起飞状态相关系数R=0.979 9,采用样本的参数估计值代替母体的参数值,得到垂直起飞状态所占时间百分比的母体统计推断值为 1.787 0。分别采用样本的非参数置信区间方法,则可得到垂直起飞状态所占时间百分比母体统计对应于置信度为90%的双侧置信区间[1.600 7,2.060 3]。
采用上述同样的母体分布类型检验及推断方法,分别对飞行谱中剩余50个飞行状态的时间百分比进行母体分布类型的统计检验和母体均值统计推断,得到各飞行状态母体最佳分布类型和时间百分比推断计算结果,如图3~图8所示。
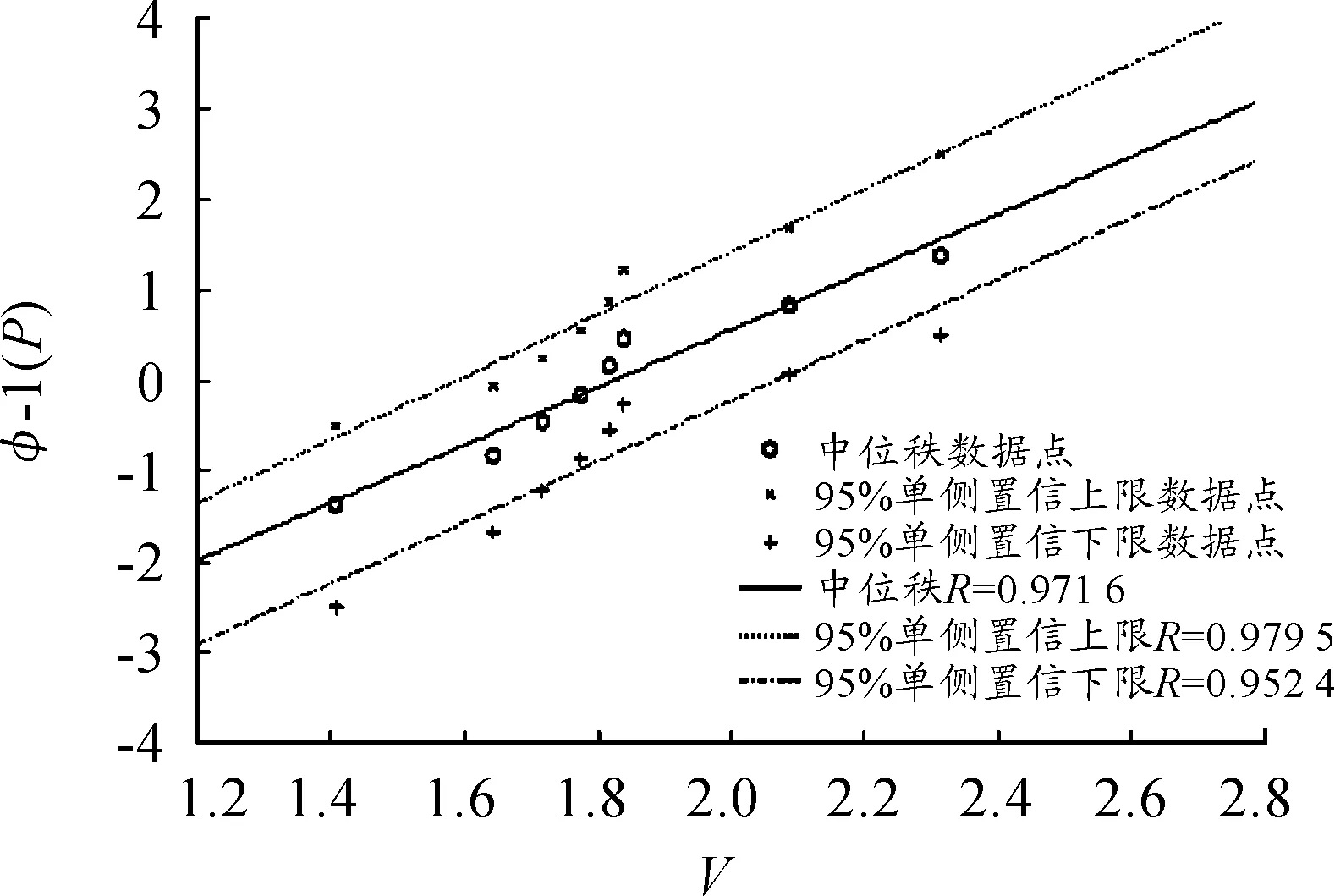
图3 正态分布回归分析
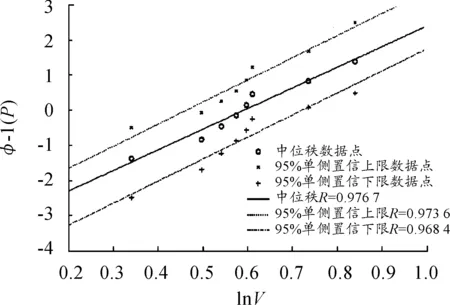
图4 对数正态分布回归分析
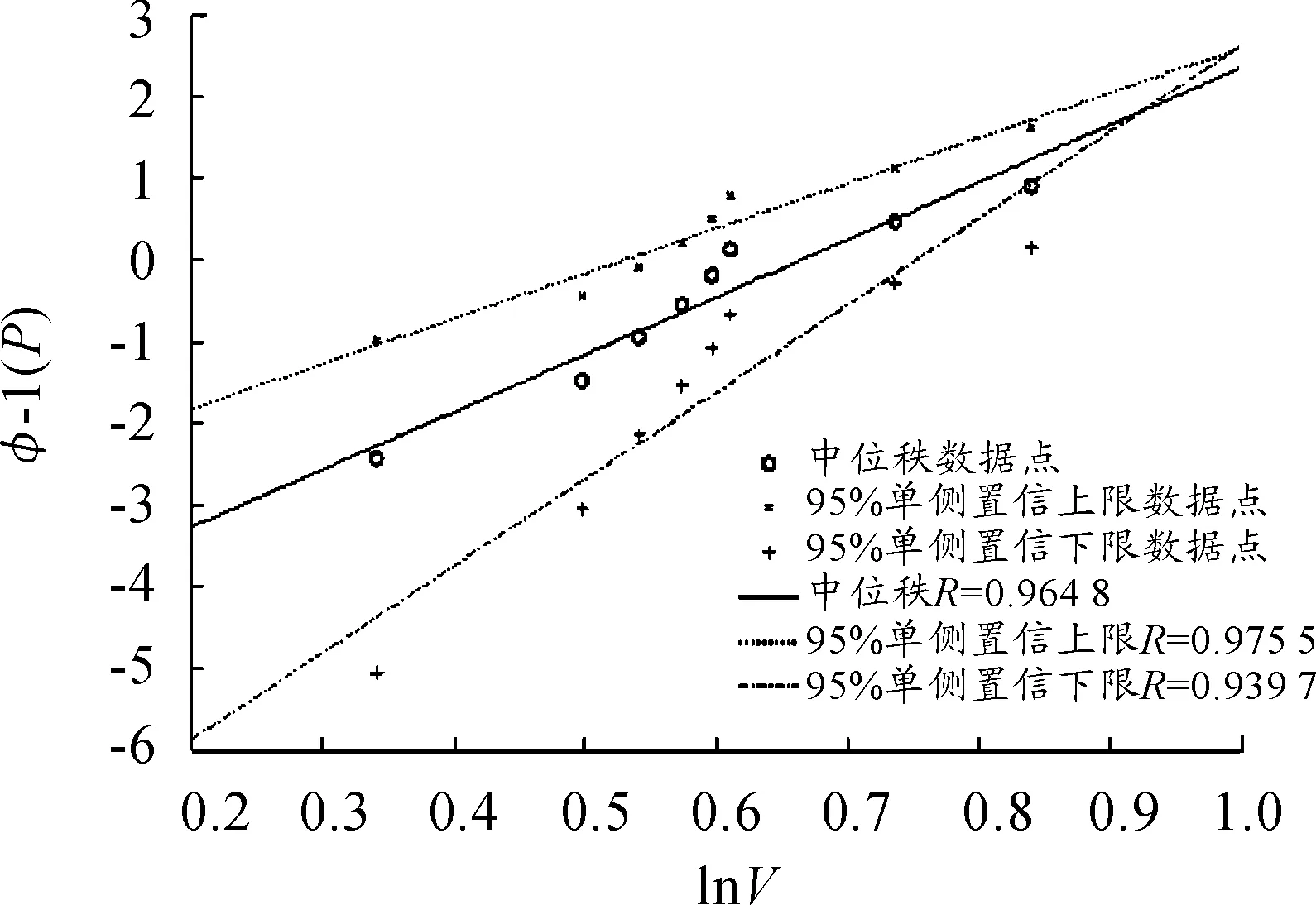
图5 双参数Weibull回归分析

图6 Gumbel分布回归分析

图7 累计概率分布拟合曲线
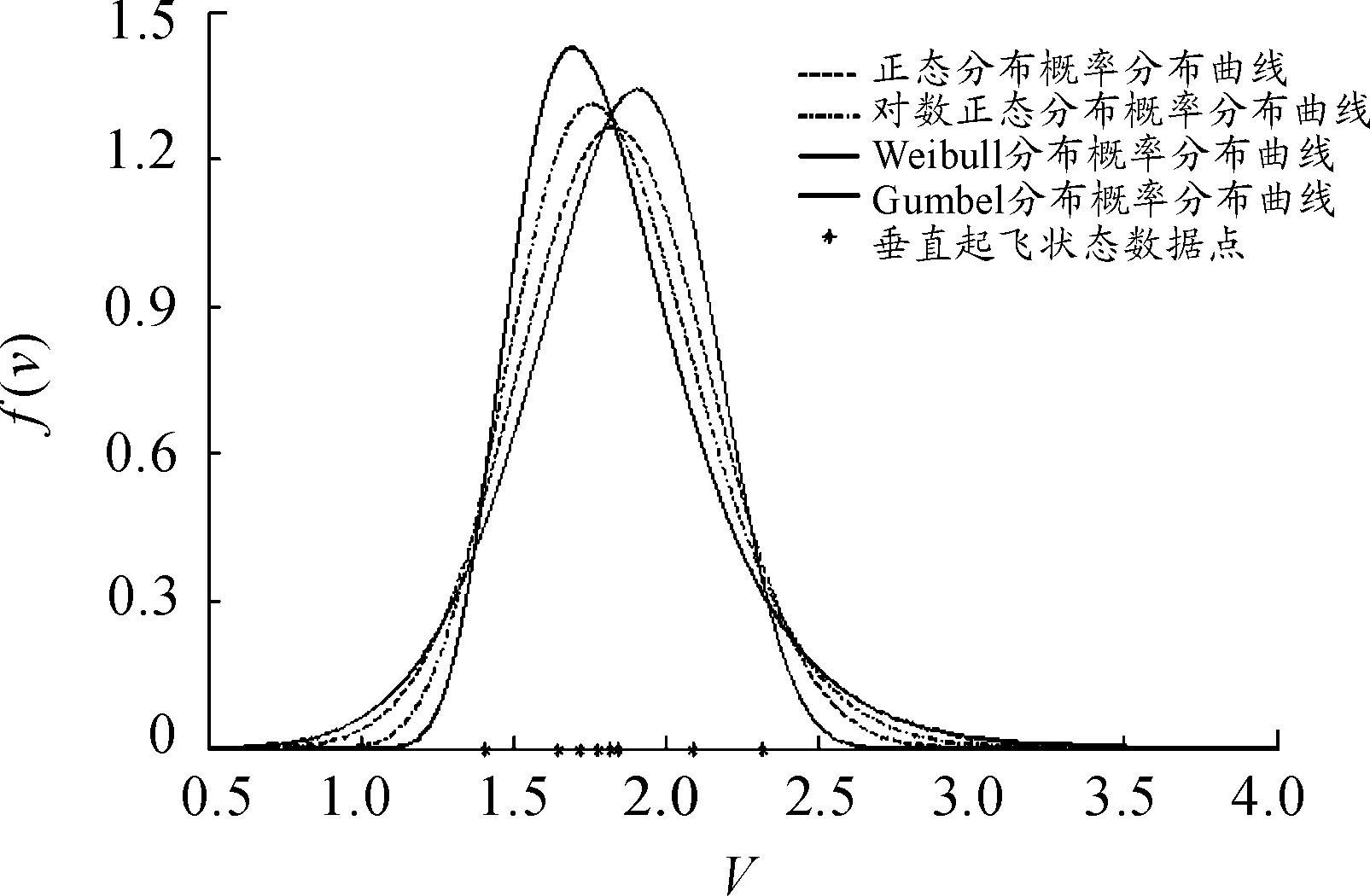
图8 概率密度函数曲线
最后,确定飞行谱加权因子。经分析,按照某两次任务中,直升机使用数量占总数量的比例,使用飞行谱加权比例因子按如下方法确定较为合理:
3 使用飞行谱可靠性分析及应用验证
根据Simth John的《“应力严重系数法”在直升机主桨叶寿命评估中的应用》所建立的计算模型,采用应力严重系数法和实测载荷谱对主桨叶根部接头进行疲劳寿命评估计算。
主桨叶根部接头螺栓孔对应置信度r=0.9,可靠度p=0.999 999的安全疲劳特性曲线表达式取为
主桨叶根部接头的疲劳寿命计算值为756飞行小时,而主桨叶根部接头全尺寸疲劳试验寿命为714飞行小时,说明该模型评估以高周疲劳损伤为主的桨叶接头区疲劳寿命具有较高的计算精度。
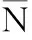
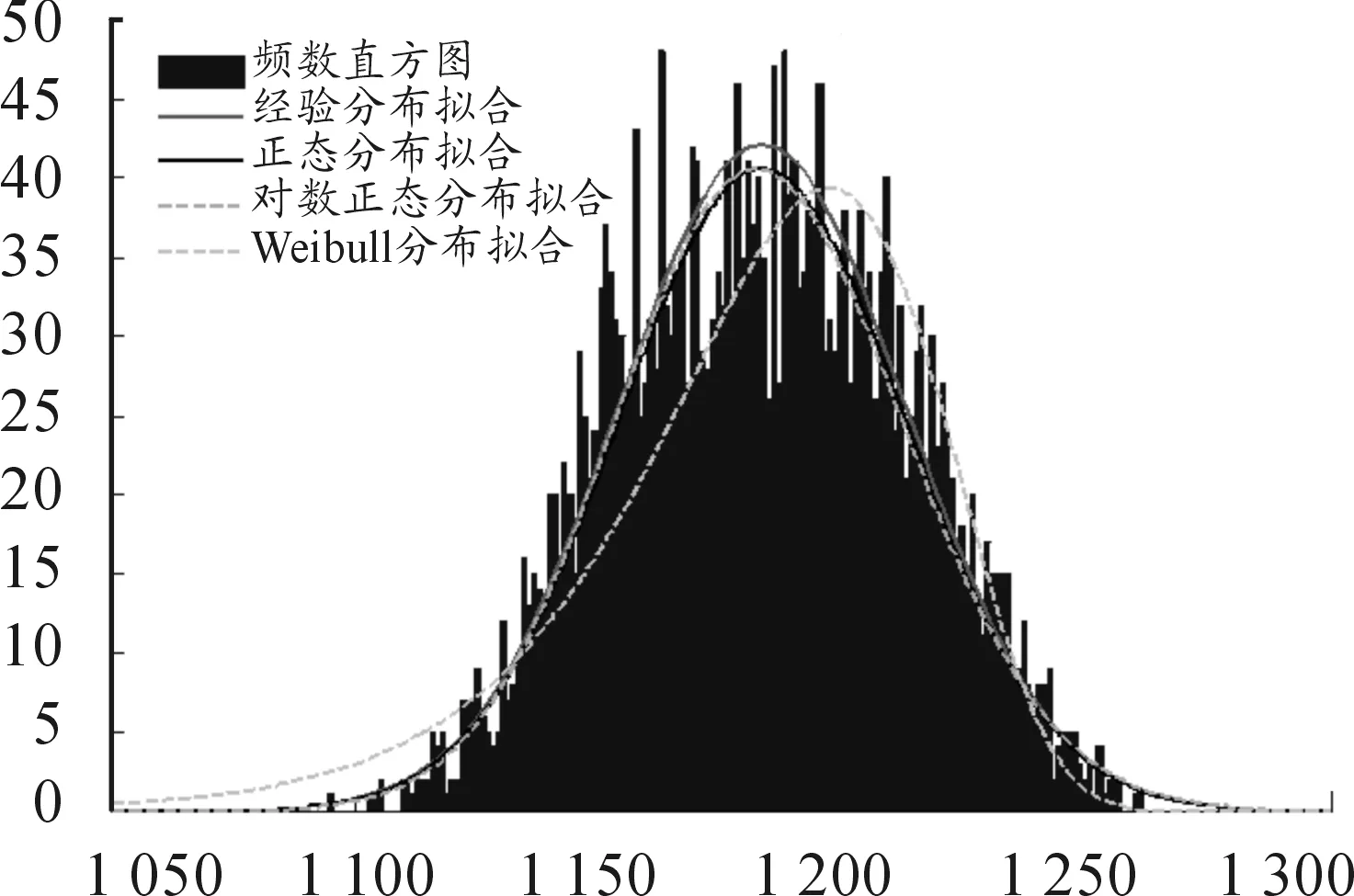
图9 陆基型使用寿命模拟值拟合图
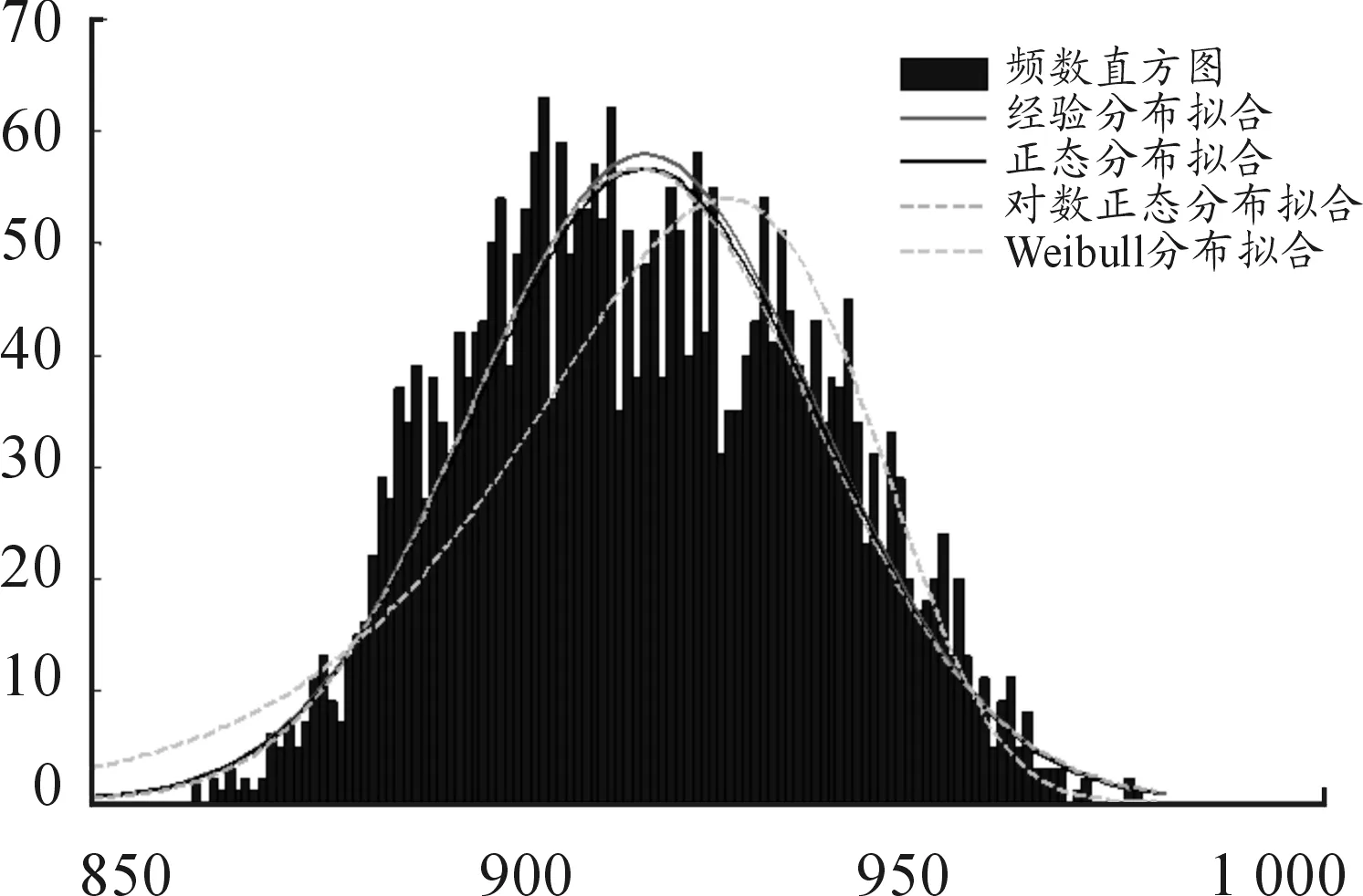
图10 舰载型使用寿命模拟值拟合图
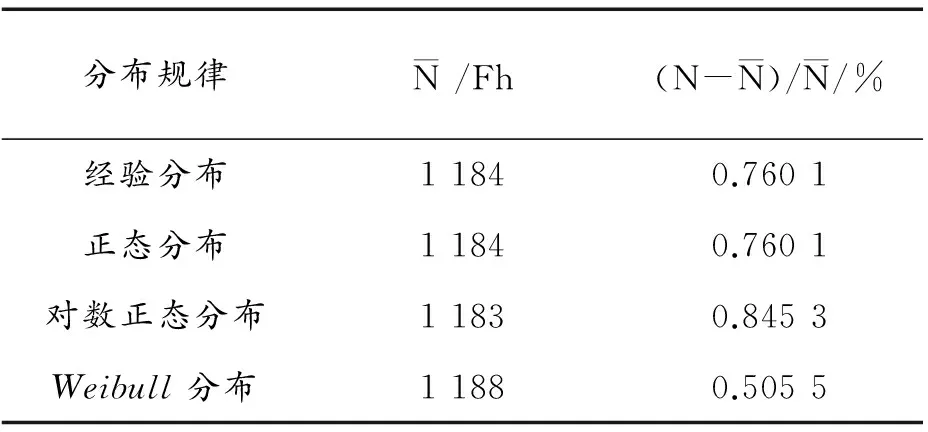
分布规律N/Fh(N-N)/N/%经验分布11840.7601正态分布11840.7601对数正态分布11830.8453Weibull分布11880.5055
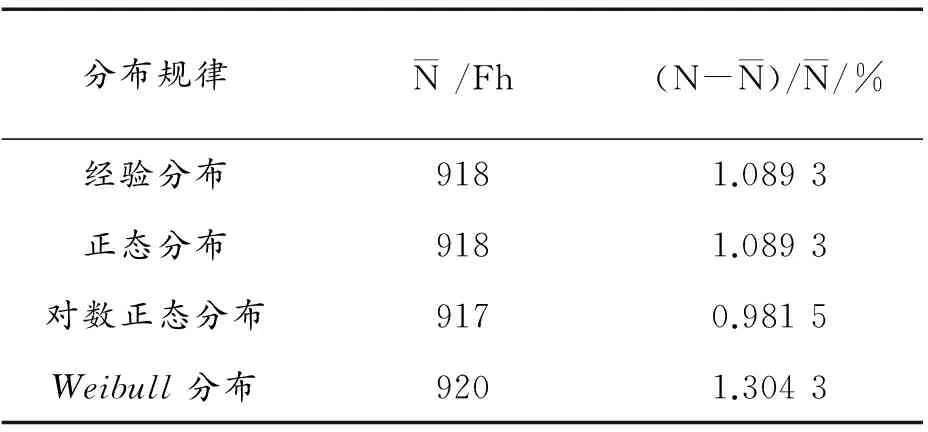
表6 舰载型使用寿命模拟值拟合均值及相对误差分析
4 结论
采用本文设计了基于概率论的直升机飞行谱编制方法,并用该方法编制了国外某型直升机使用飞行谱,经验证,该方法能较真实地反映国外某型直升机的使用情况,在使用寿命估计方面有较高的计算精度。
参考文献:
[1]高正,陈仁良.直升机飞行动力学[M].北京:科学出版社,2003:45-48.
[2]HANDD,MANNILAH,SMYTHP.数据挖掘原理[M].北京:机械工业出版社,2003.
[3]O’CALLAGHANJJ.AnalysisofaStall-and-SpinAccidentUsingRecordedAvionicsData[C].AIAAAtmosphericFlightMechaniceConferenceandExhibit.2008.
[4]KIMHW,KENYONAR,DURAISAMYK,etal.InteractionalAerodynamicsandAcousticsPropeller-AugmentedCompoundCoaxialHelicopter[C].AmericanHelicopterSocietySpecialistsConferenceonAeromechanics,SanFrancisco,CA,2008:23-25.
[5]BAGAIA.AerodynamicDesignoftheX2TechnologyDemostratorMainRotorBlade[C].64thAnnualForumoftheAmericanHelicopterSociety,MontrealCanada,2008.
[6]MASSONM,HIJUMMVAN,HEALEYA,etal.TheEuropeanHelicopterSafetyTeam(EHEST):EuropeanPartnershepforImproningHelicoptersafety[C].EuropeanRotorcraftForum,2008:47-59.
[7]SONLK,SCHWARTZBL.TheRelationbetweenMetacognitiveMonitoringandControl[M].AppliedMetacognition.Cambridge,Unitedkingdom:CambrigdeUniversityPress,2002:15-18.
[8]马亚龙,邵秋封,孙明.评估理论和方法及其军事应用[M].北京:国防工业出版社,2012:98-103.
(责任编辑周江川)
doi:10.11809/scbgxb2016.06.009
收稿日期:2015-10-19;修回日期:2015-12-20
作者简介:罗航(1989—),男,助理工程师,主要从事飞行器系统工程研究。
中图分类号:TJ471
文献标识码:A
文章编号:2096-2304(2016)06-0039-06
CompilingoftheHelicopterUsingFlightSpectrumBasedonProbabilityTheory
LUOHang,YANGHua-gao,JIANGYu
(MilitaryAgent’sRepresentativeRoomofNavalAviationinJingdezhenDistrict,Jingdezhen333002,China)
Abstract:Through the analysis of a foreign typical helicopter’s flight time, times andother information, the helicopter flight spectrum compiling method was designed based on probability theory, and this method was used on the helicopter flight spectrum compiling. It is verified that this method can reflect the usage of the type of the helicopter truly and the service life estimation has higher calculation accuracy.
Key words:helicopter; flight spectrum; probability theory
