基于Minkowski距离的一致聚类改进算法及应用研究

徐德刚　徐戏阳　陈晓　赵盼磊　苏志芳　谢永芳　阳春华

摘要：针对一致聚类算法中聚类数目判断不准确、聚类速度慢等问题，通过集成复杂网络中的Newman贪婪算法与谱聚类算法，提出了一种新的基于Minkowski距离的一致聚类算法。该算法利用Minkowski距离刻画样本间的相似度，根据随机游走策略，结合不同数据的特征值分布分析方法进行聚类，实现聚类数目的自动识别。实验仿真说明算法具有较少的运算时间及较高的聚类精度。结合实际铜矿泡沫浮选过程特点，将该算法应用于浮选工况分类，进一步验证了算法的有效性。

关键词：一致聚类；Minkowski距离；一致矩阵；聚类数目；工况识别

中图分类号：TP273 文献标识码：A

聚类分析作为一种有效的数据处理方法，在复杂工业工程中得到了广泛关注。近年来涌现出了多种聚类分析方法，包括层次聚类算法、划分式聚类算法（如K-modes-Huang算法等）、基于网格和密度的聚类算法（如网格密度等值线聚类算法、基于移位网格概念的密度和网格的聚类算法SGCE）等。这些聚类方法在多个领域得到广泛应用，其理论也得到不断的丰富和发展。

但是对不同结构特征的数据进行聚类分析时，现有的聚类方法遇到了难题，如相似度矩阵的选取问题、聚类数目的自动确定等。而一致聚类方法的提出，成为解决聚类问题的一种重要分析方法。该方法也称作聚类集成或划分算法，即针对某一特定的数据获得多种数目的不同聚类结果，并从中选取最能反映聚类信息的类别。在确定聚类数目方面，一致聚类方法具有特色，并为基因微阵数据、文本数据等聚类问题的解决提供了很好的思路。由于聚类过程中聚类数目的判断标准不尽相同，适用的领域也不同，其中最具有代表性的两种一致聚类方法是结合重采样或交叉验证等技术的一致聚类方法和基于迭代的一致聚类方法。但这两种一致聚类算法也存在聚类数目识别不准确等问题，主要是源于其重采样方法中最优的采样次数及迭代方法中的迭代次数不能有效且最优设定。

本文提出了一种新的基于Minkowski距离的一致聚类分析方法，充分利用数据特征分布特点，自动识别聚类的数目，从而解决一致聚类中数目不能自动设定的问题。通过Minkowski距离优化调节一致矩阵参数，能够在不同的度量下获得有效的聚类结果，且由于算法本身机制集成了多种聚类算法，该法还具备一定的鲁棒性。仿真结果表明本文算法在聚类数目的确定精度和准确度上优于其他一致聚类算法。

当前铜矿泡沫浮选过程生产环境恶劣且长期依靠人工肉眼现场监测，受到工人主观经验影响，易导致浮选工况操作波动异常，引起浮选药剂等资源和能源的浪费。随着计算机技术、图像处理技术、智能控制等领域的迅速发展，机器视觉技术在矿物泡沫浮选领域得到越来越广泛的应用，为浮选生产过程提供丰富的实时监控信息。

通过视觉图像系统及液位、压力等工艺参数传感器测量，浮选生产现场积累了大量反映矿物生产状态的泡沫图像数据和生产操作信息，如何有效地分析和利用这些数据对浮选过程工况的分类、识别及过程调控具有重要意义。为此，本文提出了基于Minkowski距离的一致聚类分析方法，并应用到铜矿泡沫浮选过程工况的判别，取得了较好的聚类效果，有助于实现生产实时工况的自动判别。

1 一致聚类方法

常规聚类分析过程中，由于单一的聚类算法无法获得对所有数据的最优聚类结果，融合多种聚类算法的一致聚类方法引起研究人员的关注。一致聚类具体算法流程如图1所示。

利用聚类算法集成的一致聚类方法的出发点主要通过进行多次采样或结合多种聚类算法对数据进行分析，获得反映数据类别信息的一致矩阵，从而进行数据的划分。一致聚类算法已在基因数据分析及文本聚类分析等应用中取得了较好的效果。当前一致聚类主要有两类算法：基于重采样的一致聚类方法和基于迭代的一致聚类分析方法。

1.1 基于重采样的一致聚类方法

基于重采样的一致聚类算法输入样本数据为D={e₁，e₂，…，e_N}，聚类方法采用谱聚类方法，一般把重采样分段采样比例设为80%，采样次数为H，聚类数目集合为K={k₁，k₂，…，k_j}（j=length（K），即设定聚类数目序列长度），输出为聚类数目集合D，一致矩阵为M。基于重采样的一致聚类算法流程如下所示：

结合重采样或交叉验证等技术来模拟原始数据的扰动，该法是通过多次运行某一聚类算法（例如随机选取起始点的K-means或基于模型的贝叶斯聚类方法等）来获得类别稳定性，提供了一种可视化的途径来观察类别数目、类别成员以及类别边界等信息。

大量实验表明，尽管该方法适合基因表达数据的聚类，但对其他类别聚类效果不佳，其原因为：重采样随机采样大部分样本，采样次数以及采样比例对算法影响大；基于重采样的一致聚类分析方法中确定聚类数目的准则不统一，算法中△（k）为不同聚类数目下CDF曲线与横轴包围面积的变化量，其最大值对应最终的聚类数目，将△（k）变化值作为判断聚类数目的标准不确定。针对这些问题，一些学者提出了基于迭代的一致聚类方法。

1.2 基于迭代的一致聚类分析方法

该方法遵循一致聚类方法的基本思路，不同之处在于不需要对样本进行重采样，而是利用了多种聚类算法分别对同一样本数据进行聚类，获得一致矩阵，并通过将随机游走的策略引入一致矩阵的分析中，获得了概率转移矩阵，然后通过分析概率转移矩阵的特征值进而确定聚类的数目。如果矩阵特征值不能明显反映聚类信息，则将一致矩阵代替相似度矩阵进行多次迭代，最终获得能够反映聚类数目的特征值分布。该法采用多种聚类算法，克服了仅采用一种聚类算法的局限性，但仍存在缺陷，包括迭代的次数及迭代终止的条件不明确性，相似度矩阵的确定方法单一，仅依赖高斯距离公式进行标度等问题。

针对上述两类聚类方法存在的问题，本文通过分析这两类方法的特点，提出了基于Minkowski距离的一致聚类分析方法，有效地避免多次迭代，能较准确地获得聚类数目信息。

2 基于Minkowski距离的一致聚类算法（CCBM）

本文提出了一种基于Minkowski距离的一致聚类数目自动识别为核心算法的一致聚类方法（CCBM-consensusclusteringbasedMinkowskidis-tance）。该方法集成多种聚类算法，与以上两种一致聚类方法不同之处在于相似度矩阵的构建及聚类算法的选择上。为了克服重采样、迭代方法采样数目和迭代次数不能有效的最优确定等缺点，考虑到Minkowski距离公式能够准确刻画数据大范围的相似度量信息，本文方法采用Minkowski距离对输入数据进行了不同的度量，从而完成参数设定并对相似度矩阵进行一致聚类，并确定最能反映聚类信息的相似度度量，不需要迭代即能较准确获得聚类数目信息。下面详细说明本文所提出的方法算法流程，如图2所示。

2.1 Minkowski距离函数的设定

相对于常规的欧式距离或高斯距离，本文采用Minkowski距离公式，如式（1）-式（2）。其中，x和y为n维样本点，p和？为距离调整参数。当p取1时，式（1）为曼哈顿距离，刻画的是数据i与j横纵坐标差值的绝对值之和；当p取2时，式（1）为欧式距离，刻画的是数据i与。j的最短距离，即对角线距离；当p取无穷大时，式（1）为切比雪夫距离，刻画的是数据i与j在某维度上的最大差值；p也可取其他值（如p=0.5，0.1等小于1的数）。不同p值构建的Minkowski距离，利用算法分析会产生不同的聚类效果。式（2）中a为可调参数，通过调整p值及？值，该距离公式能够从不同角度反映数据（主要是声值影响）的相似度信息。

本文设定3种不同的p值（p分别取1，2，3）及5类不同？值（？分别取0.1，0.2，0.5，0.8，0.9），通过公式（1）-（2）获得不同相似度矩阵的构建（共15种），并对其进行聚类分析。由于以上构建的15种距离能够较全面地刻画数据间不同角度的相似信息，因此可以结合矩阵特征值分析方法，获得数据不同的特征值分布，为获得数据的聚类数目信息提供依据。

2.2 聚类算法的集成

聚类算法的集成需要考虑不同聚类算法的特点，选择合适的聚类算法对一致聚类算法的有效集成至关重要。谱聚类算法作为划分式聚类算法之一，能够在任意形状的样本空间上聚类，并且能收敛于全局最优解。而Newman贪婪算法作为复杂网络层次式分析方法，由于其收敛速度快等优点，在数据的聚类分析中有着广泛的应用。本文主要融合两种不同Laplacian矩阵构建的谱聚类算法（如式（3）-式（4））与复杂网络中的Newman贪婪算法的改进算法，一定程度上避免了聚类算法复杂度高的缺点。其中，D为将相似度矩阵每行之和赋值到对角线上的对角矩阵，L为相似度矩阵。

2.3 聚类数目的识别

2.3.1 聚类数目的识别准则

由于相似矩阵可看作一个无向图中节点之间的邻接矩阵，样本数可看作图中的节点数，相似矩阵中的权值可看作图中节点之间的边，并可以利用边的粗细代表权值的大小。

在建立的无向图中引入随机游走策略，获得转移概率矩阵P，P=D^-1S，其中S为相似矩阵，D=diag（S·e），e是一个值全为1的向量。令σ（P）={1=λ₁≥λ₂≥…≥λ_n）作为P的谱分布，即特征值分布。经数学证明如果没有子类的划分，1=λ₁≥λ₂≥…≥λ_n中会有k个特征值[λ₁，…，λ_k]接近于1，而特征值λ_k与λ2_k+1之间的相对间距可以决定数据聚类的数目，这就为聚类数目的合理识别提供了数学依据。

2.3.2 一致相似矩阵及其特征值分布

首先确定所选择的聚类数目的序列，k=[k₂，k₂，…，k_n]，其中n为所选择类别的数目，然后分别采用3.2节的三种聚类方法；根据聚类数目k_i，i∈{1，2，…，n）进行分别聚类，共获得3×n个聚类结果，形成一致聚类矩阵M（如果第i个节点和第j个节点分到同一类，M_ij为1，否则为0）构建；最后将一致相似矩阵M代替相似矩阵S，按照随机游走策略获得转移概率矩阵P，求得P的特征值分布，并通过特征值的分布获得聚类信息。

2.3.3 确定聚类数目的一致聚类算法流程

提出的基于Minkowski距离的一致聚类算法确定聚类数目的具体算法流程如图3所示。

具体步骤如下：

结合Minkowski距离函数（如式（1）-式（2））建立样本之间不同角度的距离测量，令声∈[1，2，3]，？∈[0.1，0.2，0.5，0.8，0.9]，以尽量覆盖参数的取值（共3×5=15种表示相似信息的情况）。

1）对于任取的一组p值和？值，令k=[k₁，k₂，…，k_n]（依据所采用的数据规模，本文设k∈[8，9，10，11，12，13，14，15]，共8种聚类数目），对于每一k值，分别对距离刻画的相似信息采用上述3种聚类算法进行聚类，可得到3×8=24个聚类结果，由这24个聚类的结果构建一致相似矩阵M_i（i∈1，2，…，15]）。

2）重新对值p和？值进行取值，重复前一步，最后得到15个一致相似度矩阵M=[M₁，M₂，…，M₁₅]，进而获得相应的转移概率矩阵P=[P₁，P₂，…，P15₁₅]。

3）分别对转移概率矩阵P_i（i∈[1，2，…，15]）进行特征值分解，并根据特征值之间差值判别规则获得聚类的数目。

3 基于Minkowski距离的一致聚类算法（CCBM）分析

3.1 聚类数目识别分析

本文算法优越性体现在聚类数目的自动识别问题上，能够对数据进行分析并获得准确的聚类数目信息。为了验证算法有效性，测试数据为标准数据库中的UCI数据、图形数据及人工随机数据等代表性数据，如表1所示。

本文采用具有代表性的数据包括随机5类（仿真中利用Matlab软件mvnrnd函数设置均向量分别为[1，1]，[1，6]，[6，1]，[6，6]及[3.5，3.5]，对应方差均为0.1而获得的高斯数据）、Flame图形数据、Iris数据及Wine数据（对维数较高的采用SVD降维），仿真结果如图4-图7所示。

由图4-图7可以发现，本文算法对表1中数据聚类数目的识别非常准确，可有效地判断概率转移矩阵特征值分布（统计值接近于1的特征值数目）并确定聚类数目。

3.2 聚类数目结果分析

为了对比本文一致聚类方法与其他一致聚类算法的不同，针对表1的数据，分别进行聚类分析，得到的结果如表2所示。

由表2可发现，基于迭代的一致聚类算法耗时最少，主要是由于其迭代次数较少且没有重采样和参数选择环节，但是其判断数据类别数目不准确，如Iris数据的类别判断，其迭代终止的准则不明确，因此判断聚类数目不可靠。基于重采样的一致聚类算法耗时最多，主要是由于其迭代次数较大，这是为了提高精度而选择较多迭代次数的结果，但是其判断类别数目也不准确，如随机5类数据的类别判断。本文算法由于要对Minkowski距离公式参数进行选择，故耗时多于基于迭代的一致聚类算法，但是参数选择种类相对固定，耗时少于基于重采样的一致聚类算法。本文算法对于表1中4类数据聚类数目的判断准确，在聚类数目的识别准确性上优于其他两种一致聚类算法。

4 铜矿泡沫浮选的工况识别

在某企业铜矿泡沫浮选厂中铜优粗选流程如图8所示。铜矿石经过球磨粉碎过程，磨矿后的矿浆首先经过抑泥槽，后接搅拌槽，再通过粗选首槽（槽I）和粗选槽Ⅱ，其中矿物泡沫到精选过程，而矿浆到扫选过程。根据该流程生产工艺特点获知，对浮选生产有关键作用的是铜优浮选过程的粗选首槽。

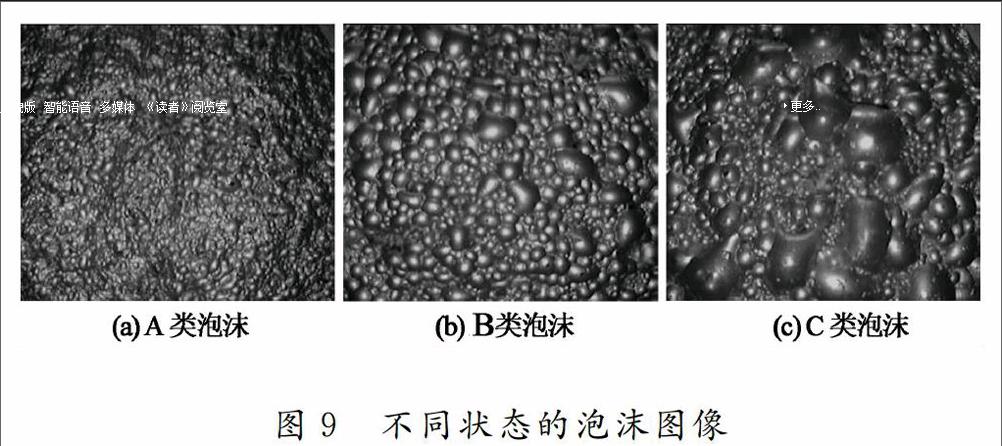
在浮选过程人矿条件稳定的情况下，首槽泡沫会随着生产操作参数的改变发生变化。因此，根据浮选泡沫的表观形状和其带矿量的多少，可以将铜优浮选粗选首槽泡沫进行工况分类，并将分类结果对应相应的操作变量，以给出合理的操作建议，指导操作。如图9所示为浮选泡沫图像的3种不同浮选生产状态，铜矿泡沫形态的特征可以分别描述为：

A类泡沫：泡沫粒径、形状不规则，多为细长的扁形且以连生体存在，泡沫间的边缘不明显，矿化程度高，含泥多，泡沫负荷过多，泡沫颜色泛白、粘稠、稳定度高，但泡沫尺寸小、速度慢。

B类泡沫：泡沫颜色、大小适中、形状规则，气泡上有坚实的矿物负荷。

C类泡沫：泡沫上负荷量减少，泡沫多为虚泡、不稳定、易破裂或兼并。

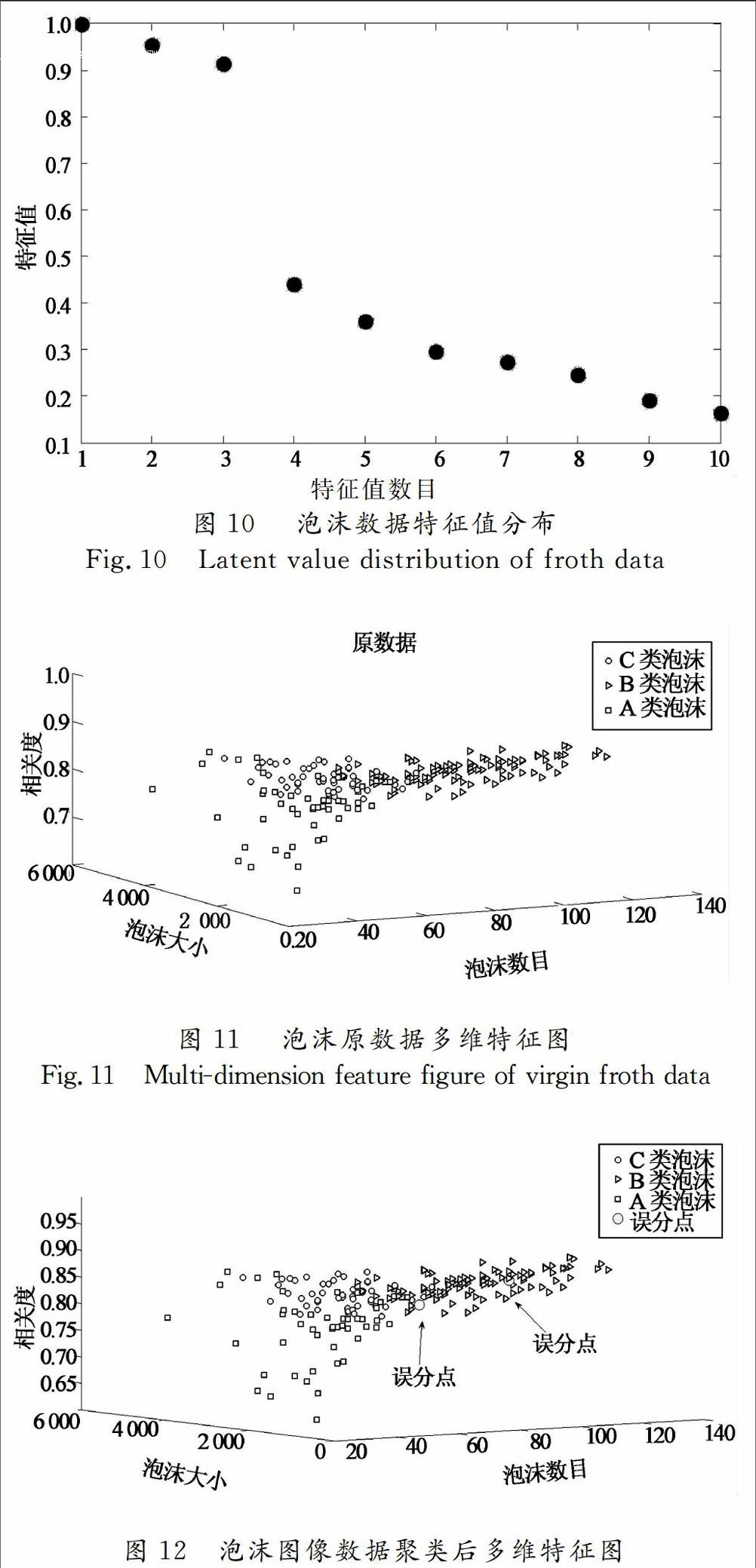
通过现场观察和生产指标分析对比研究，在这3类浮选生产状态中，B类状态对应泡沫含矿最多。由于在铜优浮选粗选首槽已经构建由高分辨率工业摄像机、高频光源及高性能工业控制计算机等设备组成的泡沫图像采集平台，准确提取了反映生产工况的泡沫表征特征（包括纹理、大小、颜色等）。针对图9所示的3类泡沫图像特征，随机选取了实际生产过程的1个月200组数据，其中A，B，C类数据分别为50，100，50组数据，对其采用基于Minkowski距离的一致聚类算法分析，一致矩阵特征值分布如图10所示。由图可见，可以明显划分为3类工况，数据聚类的结果准确性高。原数据和聚类后的数据分别如图11和图12所示。

通过对比分析发现选取200组数据中只有2个误分点，正确率达到98.5%。因此，本文所提算法可用于实际铜矿泡沫浮选过程图像数据的有效聚类，从而有助于进一步实现浮选生产工况的自动识别，识别浮选泡沫生产状态，为浮选生产操作提供指导。

5 结论

针对常规聚类算法中相似度矩阵的选取问题、聚类数目的自动确定等问题，本文提出了基于Minkowski距离的一致聚类分析方法。该方法利用Minkowski距离公式对数据进行不同角度度量，集成多种聚类算法进行聚类，根据随机游走策略，并将获取的一致矩阵转化为概率转移矩阵，结合不同数据的特征值分布分析方法确定类别数目，实现自动聚类。通过对标准数据实验对比表明算法具有较快的运算速度和较高的类别划分准确度。将本文算法应用到铜矿泡沫浮选过程工况分类效果，进一步验证算法有效性，也为泡沫浮选工况自动识别及生成过程操作提供了指导信息。