基于极坐标Hough变换的焊点检测标定方法

梁桥康　聂军平　邹坤霖　王耀南　孙炜

摘要：针对探头在粗定位情况下对车身焊点检测效率和准确率方面存在的不足，提出了一种结合焊点形态结构特点，利用极坐标Hough变换算法和改进的边缘检测算子，以精确获取焊点坐标的方法。此方法通过形态结构决策降低参数存储，用极坐标构造二维参数极大地提高了运算速度，再结合滤波、最小二乘法、双阈值法等算法，能在高噪声的背景下对焊点进行检测标定，以提高机械臂末端探头检测焊点质量的效率和准确率，对于工业上车身焊点检测具有重要的实际意义。实验结果表明，该方法处理焊点图像的准确率达到99.2%，且快速性也有很大的提高。

关键词：焊点；形态结构；极坐标Hough变换；高斯梯度；最小二乘

中图分类号：TP391 文献标识码：A

在工业4.0智能工厂的加速推动下，企业的智能化、创新和生产效率将提到一个新的高度，汽车行业的加工将变得更加智能化、精确化、高效化等。完成焊接但是未涂装之前的车身即白车身，其焊点质量关系到整车的基本性能，用CAE工具选定的关键区域对整车的性能影响更大，所以其质量检测更是必不可少。由于运用人工来检测焊点具有视觉疲劳等不可克服的缺点，同时白车身焊点检测技术正处在一个高速发展的时期，运用机器视觉技术识别焊点并进行精确定位，来提高超声波探头检测焊点的效率和准确率将成为一个必然的途径。为此，文章对白车身焊点的检测标定方法进行研究。

点焊作为白车身主要的车身装配工艺形式，由于车身结构点焊的原因，所需检测的焊点大部分为圆或近似圆形。当前对于圆检测理论的研究也比较多，常用的检测方法有环路积分微分法、颜色分类法和Hough变换检测法。Hough变换是目前应用最为广泛的圆检测方法，也是国内外研究最多的方法。该方法的优点是可靠性高，对于噪声、区域部分缺失的情况仍能检测比较准确，但缺点是运算量大，存储空间消耗大。针对此问题国内外对此提出了多种改进方法，Xu F等在工业机器人装配减速器过程中提出了一种改进型Hough变换，但在模糊边缘时检测效果不理想；Illingworth等提出了自适应Hough变换，用一个累加器数组和灵活的迭代搜索Hough参数空间的峰值；Kultanen等提出了随机Hough变换（RHT）及改进算法，在图像空间随机选取不共线的三点映射到参数空间的一个点，实现多到一的映射；Ichikawa等提出了用一维累计数组的快速Hough变换，运用局部极值点这一维数组来决定圆的方程；林金龙等提出了用点Hough变换实现圆的检测，采用固定距离取点和中垂线必过圆心的方法来确定圆的参数空间；袁卫鹏等提出了模糊随机Hough变换算法，将模糊规则融合随机Hough变换能有效地避免检出错误曲线的情况。以上学者提出方法大多基于图像噪声较小，边缘检测得到的点集比较集中时可以取得比较理想的效果，而白车身焊点噪声干扰较大，边缘并不齐整，容易检测出多个虚假圆。本文针对焊点特性进行研究，提出的焊点形态结构和极坐标Hough变换，以及改进的边缘检测算子，能在正确率和快速性方面取得比较理想的效果。

1 总体技术方案

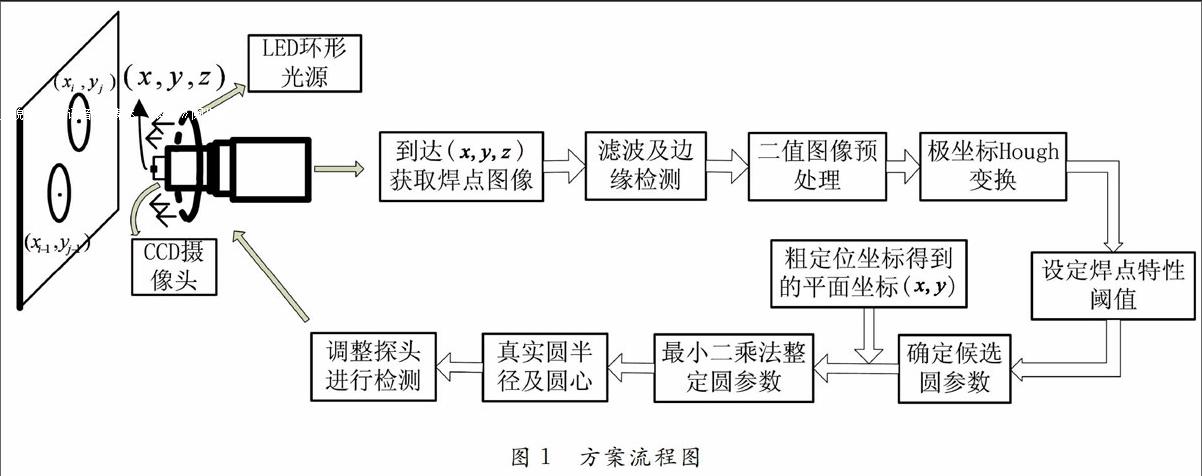
本文方案是在焊点检测时机器人通过示教得到粗步定位，使得CCD相机能垂直于车身表面，然后控制相机在环形LED光源下获取焊点图像，相机将图像传给计算机进行一系列处理，得到焊点精确坐标，然后控制机械臂带动探头向偏差减小的方向运动，以提高探头检测焊点质量的效率和准确率。本文技术方案实现的总流程图如图1所示。

1.1 滤波及改进的边缘检测

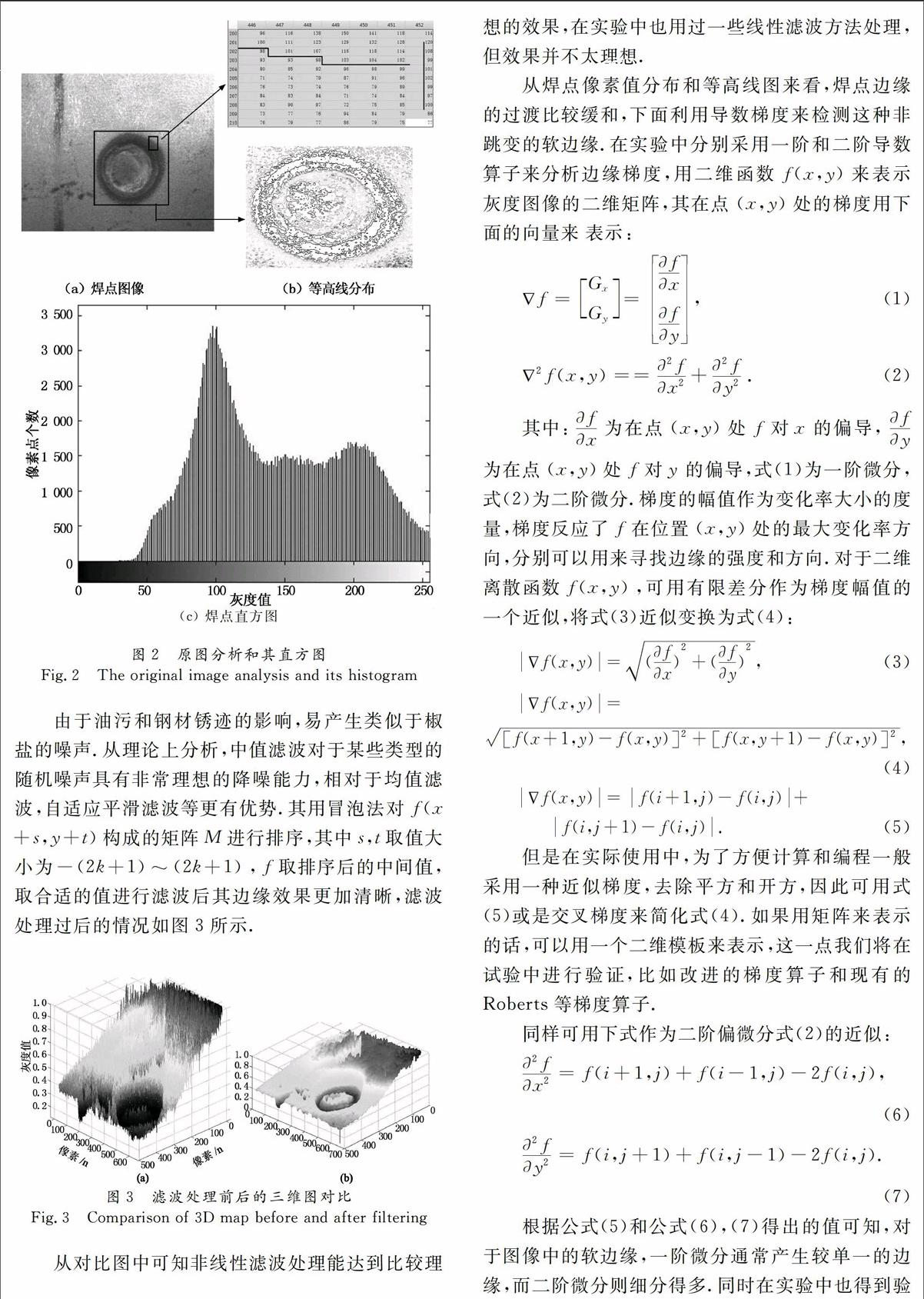
在实验中由于遮挡等光线原因容易使获取图像出现深色区域，极大地影响识别精度，为此在摄像头前端安装均匀环形光源，使获得的图像具有大体一致且满足实验条件的背景，实验中获取分辨率为640×480的图像如图2（a）所示，由图像得到其直方图如图2（c）所示，焊点的等高线如图2（b）所示，可知焊点图像的像素值集中在90到230之间，且焊点边缘模糊，属于噪声干扰比较大的一种情况。

由于油污和钢材锈迹的影响，易产生类似于椒盐的噪声。从理论上分析，中值滤波对于某些类型的随机噪声具有非常理想的降噪能力，相对于均值滤波，自适应平滑滤波等更有优势。其用冒泡法对f（x+s，y+t）构成的矩阵M进行排序，其中s，t取值大小为-（2k+1）～（2k+1），f取排序后的中间值，取合适的值进行滤波后其边缘效果更加清晰，滤波处理过后的情况如图3所示。

从对比图中可知非线性滤波处理能达到比较理想的效果，在实验中也用过一些线性滤波方法处理，但效果并不太理想。

从焊点像素值分布和等高线图来看，焊点边缘的过渡比较缓和，下面利用导数梯度来检测这种非跳变的软边缘。在实验中分别采用一阶和二阶导数算子来分析边缘梯度，用二维函数f（x，y）来表示灰度图像的二维矩阵，其在点（x，y）处的梯度用下面的向量来表示：

但是在实际使用中，为了方便计算和编程一般采用一种近似梯度，去除平方和开方，因此可用式（5）或是交叉梯度来简化式（4）。如果用矩阵来表示的话，可以用一个二维模板来表示，这一点我们将在试验中进行验证，比如改进的梯度算子和现有的Roberts等梯度算子。

同样可用下式作为二阶偏微分式（2）的近似：

根据公式（5）和公式（6），（7）得出的值可知，对于图像中的软边缘，一阶微分通常产生较单一的边缘，而二阶微分则细分得多。同时在实验中也得到验证，二阶微分对噪声和焊点本身容易检测出双边缘的情况，导致边缘点集混乱。同时为了检测滤波的效果，图4给出了直接进行边缘检测和在中值滤波之后进行边缘检测的结果。

从图4可知，滤波后的检测结果明显优于未滤波的检测结果，但在后面试验中发现虽然边缘轮廓相对清楚，然而软边缘引起的边缘混乱导致实验结果难以准确检测出真实的圆。结合上面分析，一阶导数检测软边缘具有优势，本文提出改进型的一阶导数算子——高斯一阶导数算子，利用高斯函数在空间和频率两个域的平滑性来克服边缘分散，其与一阶导数进行卷积能更好地去掉噪声，精简边缘点集。高斯一阶导数算子对图像进行处理相当于与一副输入图像。f（x，y）卷积，即

g（x，y）=[▽VG（x，y）]*f（x，y）。 （8）

其中G（x，y）为高斯函数，因为都为线性操作，故式（8）也可以写为：

z（x，y）=[▽G（x，y）*f（x，y）]。 （9）

它说明我们可以对高斯算子进行微分运算，然后再与图像卷积，其效果等价于在运用一阶导数算子进行边缘检测前先进行高斯滤波处理。

为求▽G的表达式，我们进行下列微分：

式（12）为改进的高斯一阶导数算子，根据上面提到的近似原理，本文结合焊点特性取合适的σ来得到二维矩阵算子。将其应用到sobel，roberts，和prewitt上分别对应G-sobel，G-roberts，G-prewitt算子，在Matlab上运行结果如图5所示。

从图5可知，改进型边缘检测效果更加理想，不但点集基数减少了，且边缘轮廓更加清晰，所以在边缘处理方面可选用图5（d）所用的改进一阶梯度算子。而二阶从边缘定位精度来看，不管是LoG运用高斯平滑和二阶导数零交叉特性检测边缘，还是canny算法都对边缘过于精确检测导致加入更多无效的点。表1为图5边缘检测留下的点集。

1.2 边缘二值图像的处理

从图5和表1可知，边缘检测后点集中还是有很多噪点，所以需要对边缘检测的图像进一步处理，除去独立的，不符合焊点形态的点。本文构造了如图6所示的结构进行遍历来取得有用的点。

令f（x，y）表示边缘检测后二值图像有效点的像素值（白色的点），结构系数的响应g（x，y）是形态结构系数与其所包围的图像像素的乘积之和：

其中，x，y分别表示像素点所在的行和列，是可变的，以便w中的元素能访间厂中的每个像素，（2m+1）×（2n+1）表示形态结构系数的大小。

如果g（x，y）的值小于2则表明f（x，y）对应的点不满足焊点形态结构要求，对该点进行以下处理。Aⁱ表示图6中的形态结构，集合D表示边缘检测留下的点集，B为处理过后的集合，然后运用下面的集合运算进行处理：

让Aⁱ在D上运行，以便Aⁱ能访问D的每一个元素，来创建一个新的集合B，运用Matlab编写程序对图6（d）进行验证，如图7所示。

从图7中可看出，经过处理过的二值图像与原图对比明显去掉了很多不必要的点，符合焊点形态的点基本保留下来了。不同图像经过形态学结构处理与未处理的对比如表2所示。

从表2可知，不同图像处理后的边缘点集都大幅减少，同时也足够用本文方法检测出正确的圆参数。从表中边缘点集的变化情况来看，形态学结构能够有效地减少Hough变换处理的基数，从而达到减少运算量和存储量的目的。

1.3 极坐标Hough变换

任意圆的方程可表示为：x²+y²+Dx+Ey+F=0。

在标准Hough变换中，对于原图像中的每一点（x_i，y_i）在参数空间都对应一个三维的圆锥，其数学表达式为：

（a-x_i）²+（b-y_j）²=r² （16）

其中a，b，r为参数空间的3个变量，在参数空间对应一簇相交于（a₀，b₀，r₀）的三维圆锥面，所以可想而知其计算量是非常大的，在现实程序中难以得到理想的效果。本文将参数坐标转化到极坐标，任意圆的极坐标形式为：

a=x-ρcosθ；b=y-ρsinxθ。 （17）

当n取上表2处理过后的边缘点集813，m为1且N取实验结果30时，可知其概率大概是1/21951，实验会造成大量无效积累和产生较大的误差。因此本文对D内所有的点进行遍历，准确率更高，计算量也小，设极径步长为p_n，极角步长为a_n，遍历过程如图8所示。

根据焊点的性质，给一个合适的p_n和a_n，得到极径的遍历基数M=（r_max-r_min）/p_n，极角的遍历基数N=2π/a_n，然后沿着图8（a）的极轴分别取值，利用M和N构造一个两层循环来积累参数空间三维矩阵P_h，通过下列计算来获得参数空间的值：

其中k，z为循环中步长累计的次数，若计算出的a，b，r在规定阈值内，将参数保存并使矩阵P_h对应的值加1，从而得到参数空间的累积值。

1.4 用最小二乘法得到圆参数及标定

在得到矩阵P_h后，通过搜索找到最大的积累值p_max（也就是落在此圆上的点最多），由于我们有时需要检测多个圆，同时边缘点集并不是精确地落在圆上，所以我们需要一个阈值T_n来设定一个容许误差。如果P_k中积累值大于P_max×T_n，则对应圆参数（a，b，r）被确定为检测到的圆参数，一般会得到几个圆参数，所以同时也会带来虚假圆的麻烦。这时我们需要用到前面提到的粗定位坐标来判断真实圆，并利用最小二乘来找出候选圆。设粗定位坐标转化到平面坐标为（a'，b'），其运算关系如下：

如果d相对于其他值差别较大，可知对应参数不是真实圆参数。通过判断d来去掉虚假圆，决定候选圆。式（22）中n即为候选圆的个数。因为焊点边缘不齐整，所以利用式（22）取候选圆的均值来确定最终的圆参数并标定。

另外，由于焊点噪声干扰比较大，如图1焊点上的黑色条状，容易产生小的虚假圆，有时也有可能产生大的虚假圆，一般也可以利用焊点特性人工设定最小半径和最大半径的双阈值法来去掉过小和过大的虚假圆。

2 实验结果

实验用Matlab编程工具实现，根据上面的理论，在试验中取20张图片验证都能准确检测到焊点，根据车身焊点大概3000～6000个估算，此方法的准确率能达到99.2%。下面分别对不同尺寸，不同类型的焊点进行验证。本算法不需要随机取点，所以每次运行都能取得同样的效果，图像处理的效果如图9所示。

图9（a）（c）（e）为拟合结果叠加到原图的效果，（b）（d）（f）分别展示了检测到的点集拟合后的效果图。从图9可知本算法对焊点的检测标定能取得比较好的效果。文献提到在合成图上用圆Hough变换（CHT），当N/S（噪声点与信号点的数量之比）达到30时，所耗时间为59.7s；文献提出的改进RHT算法，处理虹膜图像的时间约为2s，时间取50次的均值，但是当N/S达到22时，由于取点的关系使得检测结果急剧变坏，无法使用，并不适用于焊点检测。表3列出了本算法在处理以上图像时的信息，对于噪声比达到26.10时，还能得到理想的效果，但是如果油污较大或是噪声太大，使得N/S大于30时，容易检测到虚假圆。

本方法对于处理其他噪声较大的图像也具有一定的参考价值，图10为本文方法与文献方法的对比，处理图像的尺寸从小到大变化时，检测出正确圆所用时间如图10（b）所示。

从上面的结果可以知道，虽然文献通过快速傅立叶变化来计算Hough变换的卷积结果，来减少计算复杂性，但是对于处理像素值较大的图片其处理时间明显增强，在图像大于200×200时，本文方法具有明显的优势。

3 结论

从上面的分析和讨论可知，在改进的高斯一阶导数检测算子处理下，用极坐标Hough变换将标准圆Hough变换的三维参数降到二维，并用焊点形态学决策优化图像边缘，克服了内存需求大和运行时间长的缺点，同时也提高了准确率。极坐标Hough变换不仅在精度上满足要求，在与文献的对比实验可知，处理时间相对于其他改进算法也具有一定优势。同时本文在噪声处理方面明显优于随机Hough变化，用遍历的方法也避免了随机选取边缘点集带来的随机误差。所以本算法在检测焊点方面达到了预期的效果，且对于其他圆形检测领域也具有一定的参考性。在后期的改进工作中可以采用模糊控制来设定检测阈值，以及如何检测并确定非标准圆形的中心，并结合车身性能做更加合理的分析。