基于Rogowski线圈的电子式电流互感器可靠性分析

崔　　超，王嫚嫚，徐莹琳，林罗波

基于Rogowski线圈的电子式电流互感器可靠性分析

崔超1，王嫚嫚2，徐莹琳1，林罗波1

（1.华能山东石岛湾核电有限公司，山东威海264312；2.国网山东省电力公司威海供电公司，山东威海264200）

建立电子式电流互感器（ECT）的可靠性评估蒙特卡罗模型，对ECT的平均寿命、失效概率和可靠度进行模拟。结果表明，平均寿命约为62 451 h，失效概率在约3×105h后近似为零，可靠度在约5×104h时下降到0.5。通过应力分析法对ECT的平均寿命计算，结果为62 352 h。两种方法结果一致，相对误差约为0.15%，从而验证所建立的蒙特卡罗模型的正确性。

电子式电流互感器（ECT）；蒙特卡罗方法；可靠性评估；平均寿命；失效概率；可靠度

0　　引言

电流互感器是电力系统中用于电流测量和继电保护的重要设备之一，其测量准确度及可靠性对电力系统安全、稳定和经济运行有着重要的影响。迄今，电磁式电流互感器仍在电力系统中广泛使用，但这种电流互感器在应用上存在饱和后其二次侧电流波形及幅值失真的问题。随着光纤通信技术的快速发展，在电力系统将会较多地采用电子式电流互感器。电子式互感器能够直接提供数字信号给计量、保护装置，简化二次设备，提高整个系统的准确度［1-5］。然而，电子式电流互感器最终能否全面代替传统的电磁式电流互感器，取决于其长期运行的可靠性。

可靠性是指产品在规定的条件和时间内完成规定功能的能力。GB/T 20840.8—2007规定，制造方应按有关标准提供电子式电流互感器的可靠性和可信赖性资料［6］，其内容包括可维修各主件预期的平均无故障时间 （MTTF）和平均无故障间隔时间（MTBF），以及故障模式与后果分析（FMEA），其中MTBF通常用来表征平均寿命。电子式电流互感器已在国内电力系统中部分应用，但关于电子式电流互感器可靠性评估的理论分析鲜见报道。文献［7］应用元件计数法和应力分析法对直流互感器的可靠性进行了评估，仅得到的平均无故障时间这一可靠性指标；而文献［8］利用故障树法对互感器的可靠性进行了定性分析，没有给出具体的可靠性指标。

为此，利用蒙特卡罗方法对目前应用较多的基于Rogowski线圈电子式电流互感器进行可靠性评估与分析，并将平均寿命的评估结果与应力分析法的结果进行比较。

图1　　电子式电流互感器的可靠性模型

1　　电子式电流互感器可靠性评估

蒙特卡罗方法是一种以概率统计为基础的数值计算方法，也称统计试验方法或计算机随机模拟方法，该方法随计算机计算水平的不断提高而日益受到重视［9-11］。在系统可靠性分析中，采用蒙特卡罗方法主要是利用其模拟系统的寿命过程，在此基础上分析系统的可靠性特征。

蒙特卡罗方法的基本思想［12］是：当问题可以抽象为某个确定的数学问题时，应当首先建立一个恰当的概率模型，即确定某个随机事件A或随机变量X，使得待求的解等于随机事件出现的概率或随机变量的数学期望值，然后进行模拟实验，即重复多次地模拟随机事件A或随机变量X。最后对随机实验结果进行统计平均，求出A出现的频数或X的平均值作为问题的近似解。蒙特卡罗方法应用的主要步骤为：构造或描述概率过程，建立仿真模型；实现从已知概率分布抽样生成随机数；建立各种评估量。

1.1建立系统模型

由n个单元组成的系统，若当系统的任一单元失效时将引起系统失效，则这样的系统用串联系统表示［13］。对于电子式电流互感器，任何一个元器件失效都会造成整个系统的功能或性能失效，且没有冗余器件或电路作为备份，所以电子式电流互感器可以看作为一个串联系统。电子式电流互感器结构包括5个单元，即一次传感单元（Rogowski线圈［14］）、高压侧处理单元［15］、光纤传输单元［16］、低压侧处理单元和激光供能单元［17］。基于这些单元组成的串联系统如图1所示。

考虑到传统手工绕制空心线圈重复性差、准确性低的缺点和实际大规模生产的特点，一次传感单元采用PCB型Rogowski线圈。由于低压侧根据应用的不同，需要接不同的显示装置，因此只评估其数据分析处理元件［18-19］。

1.2随机变量抽样

在每一次对系统可靠性进行评估的过程中，需要对n个基本单元的寿命进行随机抽样以取得它的失效时间样本，在此基础上进行各可靠性指标的点估算。

构成单元的器件失效时间t是一随机变量，它服从的分布称为失效分布（亦称寿命分布）。对于每一器件可用指数分布作为其失效分布的近似［20-21］。一个指数分布函数可表为

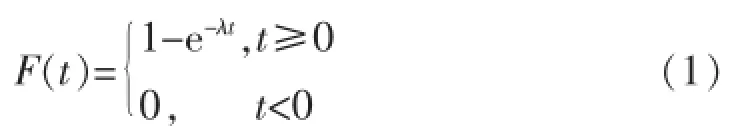
则相应的概率密度函数为

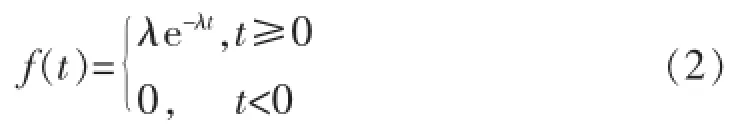
式中：λ为失效率，且为器件平均寿命θ的倒数，即λ=1/θ。

GJB/Z 299C—2006［22］给出了应力分析法和计数法评估电子设备可靠性所需要的各种失效模型和参数，是对许多工程设备进行可靠性预计的权威性依据。目前已获得我国电力系统所用电子式电流互感器详细的元器件清单及每个元器件所承受的应力数据，所以可用应力分析法分析其可靠性。根据这些参数和失效模型，计算得到的电子式电流互感器各器件的失效率如表1所示。

表1　　可靠性模型的各单元失效率

1.3可靠性指标的点估计计算

系统的主要可靠性指标有可靠度 （或不可靠度）、失效概率、系统平均寿命等。这些可靠性指标的点估算方法［23］如下。

通过N次仿真运行可获得系统失效时间的N个样本。首先设系统最大工作时间为tmax，将（0，tmax］分成m个区间（m的选择要恰当），则每个时间间隔为Δt=tmax/m。设统计第k个单元在第r个时间间隔［tr-1，tr］内系统失效数用Δmr表示，则有

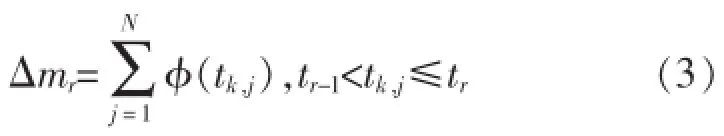
式中：φ（t）为系统的状态变量；tk，j为第j次仿真中第k个单元发生失效的时刻。当仿真过程中各单元的抽样失效时间t≥tk，j时，系统发生失效，φ（t）记为1，否则记为0，即有

式中：t为仿真过程中各单元的抽样失效时间。若统计t≤tr内的系统失效数mr，则有

在得到了系统的失效数Δmr和mr后，则可进一步统计获得系统的可靠度（或不可靠度）、失效概率分布和平均寿命。

1）系统不可靠度。

tr时刻系统不可靠度定义为

则系统不可靠度的点估计计算公式为

2）系统失效概率分布。

系统在tr时刻的失效概率分布为

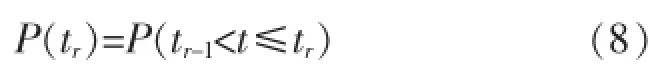
它的点估计值为

设t为系统可靠性仿真的设计模拟时间，若t足够大，以至于R^（t）=0，此时，系统平均寿命点估计值为：

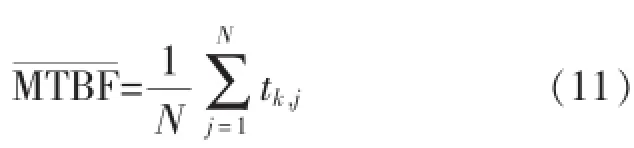
3）系统平均寿命。

系统平均寿命定义为

2　　仿真运行

2.1仿真流程

根据图1所示的电子式电流互感器可靠性模型及蒙特卡罗仿真原理，可得仿真的流程如图2所示。

2.2仿真结果及分析

按上述方法和原理，在Matlab环境下对电子式电流互感器可靠性进行仿真。仿真过程中，系统的工作时间设为5×105h，并分为200个区间进行统计。仿真计算得到的系统平均寿命MTBF=62 451 h，失效概率和可靠度随时间的变化如图3所示。系统的失效概率最大值约为0.04，且随时间逐渐减小，约在120个时间间隔（3×105h）后近似为零。此外，可靠度在约第20个时间间隔（5×104h）时下降到0.5。

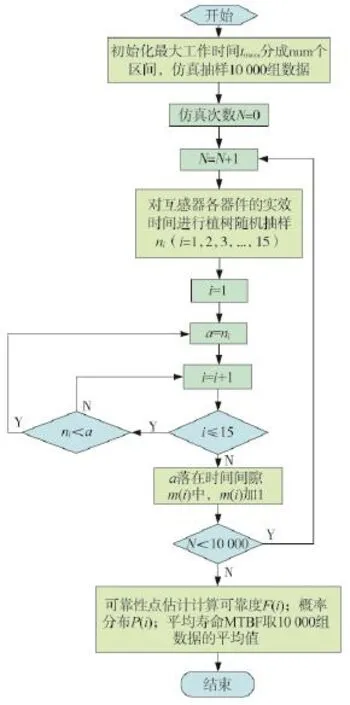
图2　　仿真流程

2.3应力分析法验证

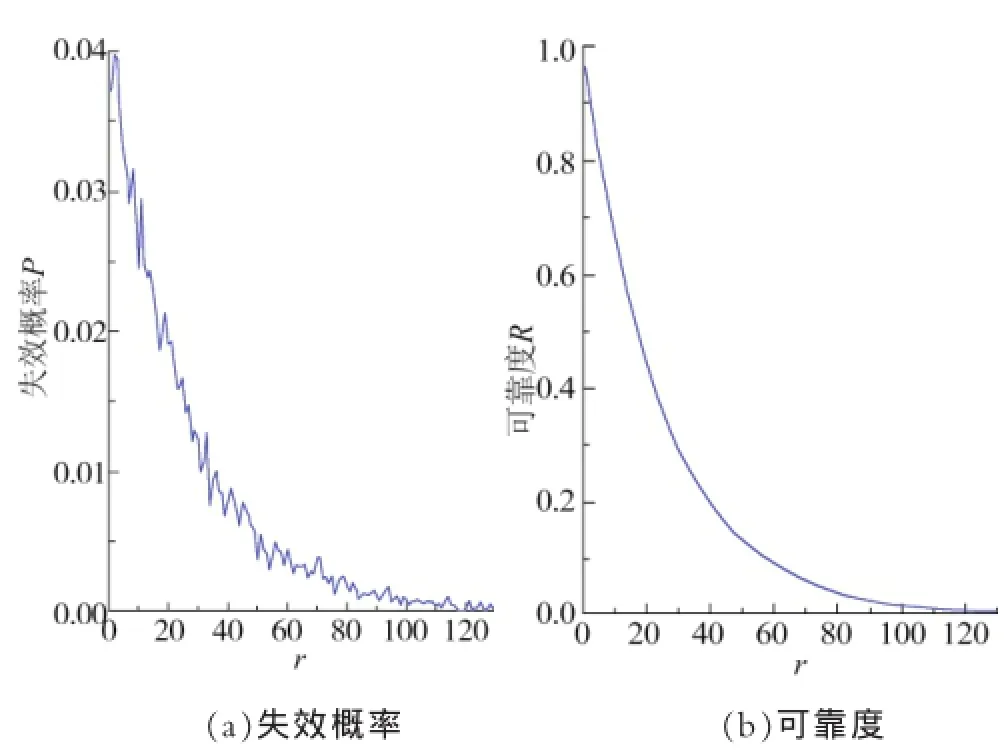
图3　　可靠性指标

使用应力分析方法［24］预计电子设备可靠性平均寿命指标MTBF，程序如下：先划分可靠性预计单元，建立系统可靠性模型；按工作失效率模型计算各分单元内元器件的工作失效率；将预计单元内各种类元器件的工作失效率相加，由此得出预计单元的失效率；按设备、系统的可靠性模型逐级预计设备、系统的平均寿命。

应力分析法对于每个器件的失效率

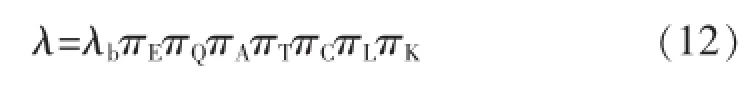
式中：λb为器件的基本失效率；πE为环境系数；πQ为质量系数；πA为应用系数；πT为温度应力系数；πC为结构系数；πL为成熟系数；πK为种类系数。

对表1的数据进行可靠性分析，得到的系统失效率是16.037 08×10-6/h，则平均寿命MTBF=1/λ= 62 352 h。可以看到，该结果与蒙特卡罗模拟的结果一致，相对误差约为0.15%，从而验证了所建立蒙特卡罗模型的正确性。

3　　结语

建立基于典型的电子式电流互感器的可靠性评估蒙特卡罗模型，并应用建立的模型对该电流互感器的可靠性进行了评估。计算的平均寿命约为6.245 1×104h，失效概率在约3×105h后近似为零，可靠度在约5×104h时下降到0.5。并且基于应力分析法对所考虑的电子式电流互感器的平均寿命计算，结果为62 352 h。两种方法模拟结果的相对误差约为0.15%，验证了所建立蒙特卡罗模型的正确性。

［1]张廷成.电子式电流互感器的研究［D］.哈尔滨：哈尔滨工程大学，2008.

［2]龚伟.电子式电流互感器传感头的研究与设计［D］.长沙：湖南大学，2009.

［3］ 赵冠.有源电子式互感器的研究与设计［D］.济南：山东大学，2010.

［4］ 王鹏.电子式互感器数据采集系统的研究与设计［D］.大连：大连理工大学，2009.

［5]吴士普.激光供电的光电电流互感器研究［D］.武汉：华中科技大学，2004.

［6］GB/T 20840.8—2007互感器第8部分：电子式电流互感器［S］.

［7］ 张艳，李红斌.用于HVDC的电子式直流互感器的可靠性预计［J］.高电压技术，2007，33（7）：119-123.

［8]王鹏，张贵新，朱小梅，等.基于故障模式与后果分析及故障树法的电子式电流互感器可靠性分析［J］.电网技术，2006，30（23）：15-20.

［9]王世香，高仕斌.蒙特卡罗方法在变电站综合自动化可靠性评估中的应用［J］.电网技术，2006，30（5）：96-100.

［10］袁立峰，王浚.可靠性数字仿真方法及其应用［J］.电子产品可靠性与环境试验，2005（2）：17-20.

［11］CHUL Kim，HOE K，LEE Y.A Monte Carlo Simulation Algo rithm for Finding MTBF［J］.IEEE Transactions on Reliability，1992（2）：193-195.

［12］马文淦.计算物理学［M］.北京：科学出版社，2006.

［13］高社生.可靠性理论与工程应用［M］.北京：国防工业出版社，2002.

［14］张艳，李红斌.PCB型Rogowski线圈的可靠性研究［J］.高压电器，2006，42（12）：421-427.

［15］董郁，张太利.电子式控制器的可靠性分析和研究［J］.低压电器，2011（1）：13-17.

［16］方志，赵中原，邱毓昌，等.用于混合式光电电流互感器的光电传输系统［J］.电网技术，2007，27（4）：43-45.

［17］钱政.有源电子式电流互感器中高压侧电路的供能方法［J］.高压电器，2004，40（2）：135-138.

［18］刘琨，周有庆，彭红海.电子式互感器合并单元（MU）的研究与设计［J］.电力自动化设备，2006，26（4）：67-71.

［19］刘曲波，李红斌，谢经东.GPS时钟同步在电子互感器合并单元的中的应用［J］.电气应用，2007，26（5）：42-44.

［20］郭水旺，胡乾坤.基于蒙特卡罗的电子产品可靠性分析［J］.电子与封装，2010，10（5）：33-35.

［21］张黎.电气设备寿命分布分析［D］.济南：山东大学，2005.

［22］GJB/Z 299C—2006电子设备可靠性预计手册［S］.

［23］肖刚，李家柁.系统可靠性分析中的蒙特卡罗方法［M］.北京：科学出版社，2003.

［24］MIL-HDBK-338B电子设备可靠性设计手册［S］.

Reliability Prediction of Electronic Current Transformer Based on Rogowski Coil

CUI Chao1，WANG Manman2，XU Yinglin1，LIN Luobo1
（1.Huaneng Shandong Shidao Bay Nuclear Power Co.，Ltd.，Weihai 264312，China；2.State Grid Weihai Power Supply Company，Weihai 264200，China）

An reliability Monte Carlo model of electronic current transformer was established，by which the average life，failure probability and reliability of the current transformer were evaluated.Calculated results showed that the average life was about 62 451 hours，and the failure probability was approximately zero after 3×105hours，and the reliability dropped to 0.5 after 5×104hours.The average life of the current transformer calculated by the part stress analysis was 62 352 hours.Compared with the result by Monte Carlo method，the relative error was within 0.15%，which indicated that the Monte Carlo model was accurate and reliable.

electronic current transformer（ECT）；Monte Carlo method；reliability evaluation；average life；failure probability；reliability

TM930

A

1007-9904（2016）06-0014-04

2016-01-13

崔超（1986），男，工程师，从事电厂继电保护及发电机励磁系统调试工作；王嫚嫚（1987），女，工程师，从事变电站继电保护及自动化系统检修工作；徐莹琳（1987），女，工程师，从事电厂继电保护及自动化系统调试工作；林罗波（1988），女，工程师，从事电厂继电保护及自动化系统调试工作。