变形监测回归分析模型的优化改进
2016-08-11申意保湖南省地质调查院湖南湘潭411100
申意保(湖南省地质调查院,湖南 湘潭 411100)
变形监测回归分析模型的优化改进
申意保(湖南省地质调查院,湖南湘潭411100)
关于数据处理理论和方法的研究对变形监测有着十分重要的意义。变形监测数据处理方法主要分为平差处理和拟合预测两个部分。本文主要针对变形监测的拟合预测部分展开分析和研究。论述了常用的回归分析方法。运用初等函数理论,定义了一种关联度分析方法和关联系数。以此来提高建立模型的效率和质量。也使得到的拟合预测模型精度更高。并用算例进行验证。证明了模型改进的有效性。
变形监测;拟合预测;相关度;步长;初等函数;回归分析
1 引言
城市建设越来越快。高层建筑物和大型工程在施工和运营期间,会产生变形,如果产生变形超过了工程主体的极限和规定的限度,就会危及建筑物安全。因此,我们需要在工程建设与运营过程中,对其进行变形安全监测[1]。变形监测的准确性就显得很重要了。增加变形监测准确性主要包括两部分:在数据采集上,通过研制先进的观测仪器来提高采集数据的质量。在处理数据时,包括平差方法和预报模型,不断寻求新的理论方法和模型[2]。本文主要对数据处理的常用预报模型——“回归分析”进行分析和改进。
2 回归分析模型
回归分析模型是一种传统的数据分析方法,也是最成熟的方法之一。可以建立和单因子的相关关系,也可以同时建立和多因子之间的相关关系。相关关系式可以是线性的,也可以是非线性的。非线性的关系可以根据曲线匹配和多项式函数拟合,通过变量转换为线性回归关系。对于具有固定相关关系的而参数不确定的也可以用回归分析进行参数求解[3]。完整的建立回归分析应包括:
(1)因素分析;
(2)模型的建立;
(3)相关性检验;
(4)预测。
建立模型:分析影响因子和监测值相关关系;
建立回归模型为:

式中:yi为监测值应变量;β0为截距;β1,…,βm为系数;xij为自变量;εi为随机误差项。
模型误差方程有:

有最小二乘参数解β=(ATA)-1ATY
得到自变量与因变量的回归方程:

模型检验:对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断[4]。检验统计量是:

3 模型优化分析
线性回归提出的是影响因子的后检验,就是在确立模型之后,对影响因子与观测数据的相关度进行分析。建立模型之前选取因子的好坏直接影响着模型的准确度。建立模型时,如果已经知道了观测值同影响因子的数学关系,模型的建立比较简单,但是在对相应的物理关系的不了解时,很难选取合适的影响因子。从而无法构建相应的数学方程。因此如何在建模前对影响因子检验就很重要了[5]。
建立一种分析方法——关联系数分析方法。根据影响因子的发展趋势和观测量的趋势相似度。并将关联程度进行量化。关联系数分析方法是以反应变化趋势为立足点。因此对样本的值大小没有很大的要求。
影响因子和观测值的数学关系可以写成函数表达式,而函数形式是数学里的基本初等函数:
(1)常数函数y=c(c为常数);
(2)幂函数y=x^a(a为常数);
(3)指数函数y=a^x(a>0,a≠1);
(4)对数函数y=log(a)x(a>0,a≠1,真数x>0);
(5)三角函数:正弦函数y=sinx;余弦函数y=cosx等。
由于函数中都含有未定a常数。将预先定义常数值。幂函数,α=-∞,…,0,…∞。a的间隔根据需要而定,一般间隔大小为1。指数函数和对数函数a的值为常数e。
总结有单个因子同观测量的关系以下几种关系:

定义影响因子与观测值的关联系数为R:

其中k和b是根据相邻两期的观测值计算得出。

通过比较,认为R值越小,表明影响因子与测量值的相关度更大。得到影响因子同测量值最合适的数学关系式。同时也可比较不因子间的关系度。以此来在建模之前判断那种因子对观测值影响更大。
4 算例
现有高速公路其中一处滑坡体10期精密水平测得的垂直变形数据,选择了其中2个变形监测点,数据链的长度为9期,每期的间隔是14d。表1给出了这9期的观测值(其中的数据已经进行了等间距化)。
根据累计沉降值同观测期数的线画图,人为判断建立模型。
从图1中判断二次曲线同观测值比较吻合,建立的模型方程为:

式中:y为累计沉降值;x为观测期数(时间)。

表1 滑坡体10期精密水平9期累积变形沉降量(单位:mm)
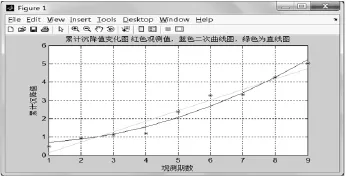
图1
有误差方程组:

最小二乘解为:

有回归分析模型方程:

同点1有:
点2:

由根据模型计算拟合值,同时与观测值比较有表2。

表2
5 模型优化算法
首先在不知道观测值和观测期数(时间)的相关关系的前提下,可以通过模糊比较比较观测期数经过不同初等变换后和观测值的相关系数来选取适合相关关系。
首先将观测期数根据初等函数,进行初等变换。
这里通过了10种初等变化函数:

构成函数形式为:

依据关联系数:
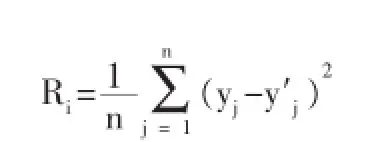
计算有见表3。

表3
从关联系数R的值比较可以得出,点1第5,6,7个函数关系对模型的影响为一个水平。点2中第5,6个函数关系式对模型的影响为一个水平。
下面根据对应的函数关系式建立模型:

分别计算点的拟合值以及预测值。并与实测值进行比较。见表4。

表4
优化前后各个点拟合情况对标情况见表5。

表5
通过比较各个点,可以发现通过优化后的模型比没有优化的模型所得到的结果要更好,模型的拟合度更高,观测值与拟合值的差值平方和有显著减小。拟合预测的结果与实测数据更加吻合。说明了模型的优化是有效的。
6 总结
本文旨在变形监测采用回归模型进行拟合预测过程中,在模型不确定的情况下,通过关联系数分析方法,以基本初等函数为分析单元,对回归模型的建立进行优化。以初等函数为基本关系式建立数学关系,优化模型结构。通过算例计算,表明模型的优化是有效的。在实际应用过程中也是具有价值的。
[1]朱健.建筑物变形监测数据分析中的灰色改进模型应用研究[D].西安:长安大学,2007.
[2]黄声享,尹 晖,蒋 征.变形监测数据处理[M].武汉:武汉大学出版社,2003.
[3]张俊中,宋 蕾,张健雄.多元回归分析模型在变形监测中的应用[J].河南工程学院学报(自然科学报),2009.
[4]俞能福.多元线性回归在分析学生成绩相关性中的应用[J].大学数学,2007.
[5]何晓群,刘文卿.应用回归分析(第三版)[M].北京:中国人民大学出版社,2011.
申意保(1970-),男,工程师,本科,主要从事工程测量工作。
TU196.1
A
2095-2066(2016)11-0021-02
2016-3-27
