基于时序相关性的信息效用评价模型研究

杜晓艳

(深圳大学 图书馆，广东　深圳　518060)



基于时序相关性的信息效用评价模型研究

杜晓艳

(深圳大学 图书馆，广东深圳518060)

事务处理中的时间相关性数据蕴涵着对预测与决策具有情报效用的信息，可以通过构建一定的特征模式对其效用大小进行评价。文章对时变序列数据的相关性特征进行了分析，研究了基于时序与波动变化的特征抽取模式；在时变序列的差分及相对变化基础上，进一步综合利用偏态、离散、相关等特征构建了影响变量与响应变量之间的相关度计算模型。该模型可降低效用评价计算复杂度，增强评价的可靠性并可用于模型预测。

时序特征；相关性；特征模式；信息效用;信息资源

一、引　言

按照服务职能，信息系统包括事务处理系统、管理系统、决策支持系统、人工智能/专家系统。[1]因此，在决策支持系统层次会产生自下而上的信息流动及相关的信息资源转换，将信息资源提升为知识资源，充分发挥信息资源的作用。[2]但是，在不确定性日益增强的自然与社会环境中，信息量不断膨胀及不确定性日益增加，信息的数据结构与表现方式也日趋多元与复杂，呈现出大数据或准大数据环境特征。在大数据环境下，数字信息资源具有连续性、周期性、高维度、高自由度等非线性特征。数据虽然价值越来越大，但价值密度低，数据挖掘难度大。这些因素使决策层与其他相关层次的信息协作与转换流程更加复杂，极大地影响决策情报实时形成的效率与可靠性。

因此，针对事务处理中信息系统历史数据体量大、价值密度低、时序性强、非随机性及速度要求高等处理特点，需要建立简单、快速的数据分析与约简模型，通过建立一定的特征模式来降低信息情报效用评价的维度以获得更高的计算效率，满足决策与预测实时性与可靠性的要求。

二、信息效用评价模型和要素分析

目前针对信息的决策效用价值评价研究主要集中于两个方面：一是针对信息效用评价指标体系的构建，以定性研究为主，如面向历史档案的情报效用，提出针对档案信息情报效用的评价体系，包括知识发现难易程度、需求量、可获取性和使用效果[3]；二是基于定量评价的概率模型或线性效用模型，如基于某个具体任务的完成对用户的有用程度，提出面向任务网络的信息效用度量标准、平均认知评分等。[4]

基于预测、决策需要的信息一般分为两类：一类是完全信息，即可以得到肯定答案的客观状态的信息；另一类是抽样信息，一般通过调查或抽样获得原始信息，用统计方法来推断客观状态出现的概率[4]及对客观状态可能影响程度的大小。二者均面临信息的情报效用分析与评价问题。在具体实践中，评价的要素主要包括：一是信息单元对决策主题产生影响的程度大小，它在量化方面需要通过比较产生的相对价值来体现。这种比较应该建立在动态变化的相关性上，而相关性除了与变化本身相关外一般还与时序关系有关；二是在多元信息环境下，各影响因素之间本身存在一定的相互作用与影响，需要克服因素之间的重叠作用；再有就是抽样信息本身发生的概率，这是需要估计的先验概率。对于信息系统内基于历史数据的信息，主要应该考虑其发生变动的可能性大小，而系统外部相关信息发生可能性的大小则相对难以判断，具有更大的随机性与不确定性。

信息系统中的数据时变序列不仅蕴涵着相对影响程度的信息，也在一定程度上包含了共线性信息及先验概率信息。本文的评价模型基于事务数据所蕴含的信息，建立在被影响因素与影响因素时序变化与波动相关性基础上，具有统计确定性、过程的完整性及数据的可靠性等特性，能够通过构建的特征模型来体现评价要素的综合性。

三、抽样信息的时序特征及波动相关性

1.数据选定及预处理

假设Y是预测或决策方案中的一个重要量化指标，称为响应变量。响应变量可能受到m个变量X1，X2、，……，Xm的影响，称为影响变量。响应变量和影响变量的抽样结果，一方面可用于评价影响变量对响应变量产生影响的效用价值，另一方面可建立线性回归表达式对响应变量进行预测。

分别按照一定的时间周期间隔对响应变量和影响变量进行抽样。其中，响应变量Y抽样获得的序列为时点数列，是在具有明显变动时刻或指定变动周期的统计值；影响变量的抽样值为时变序列，序列中的值反映一定时间内指标的统计量。

假设已获得相当数量的抽样测量值。对各变量均找出相对稳定的起始值，则可获得测量值绝对时序关系，如表1所示。其中，第1行为响应变量Y及其测量值yj(j=0～n)，第2行到第(m+1)行为影响变量Xi(i=1～m)及其测量值xij。

表1　测量数据

2.基于差分的波动序列

为使评价建立在变动相关性基础上，用差分描述变量的变动情况，同时将得到的差分序列进行标准化，使变动相关性在量纲上一致。为此，定义响应变量测量值的差分序列标准化参数为：

(1)

类似地，定义影响变量测量值的差分序列标准化参数为:

(2)

对表1中的测量值分别按式(1)和式(2)进行处理，得到响应变量及影响变量增量△Y和△Xi(i=1～m)的标准化参数数据，如表2所示。各变量相对变化数据均与本身量纲无关。

表2　变量的标准化数据

3. 样本的位置度量及偏向特性

众数、中位数和算术平均数是序列的位置度量指标。众数为序列中出现最多的标志值，中位数为序列的中间值，算术平均数是序列值和的平均数[5]。同时，众数、中位数和平均数之间的大小关系反映了序列的偏向特性，它们体现了响应变量与影响变量在波动变化上的一致性状态。偏向上越接近，说明在变化方面接近程度越高，影响变量起促进作用；偏向若表现出背离形态则起反制作用；若响应变量与影响变量变化无关则相关性较小或不存在相关性。无论是促进还是制约均体现了一定程度的作用，在影响程度上同样是有价值的。

分别计算表2中各序列的众数、中位数和算术平均数，列于表3。其中，响应变量的增量△Y测量值的众数、中位数和算术平均数位于第1行，分别表示为ρ，μ，ν；影响变量的增量△Xi测量值的众数、中位数和算术平均数位于第2行到第(m+1)行，分别表示为ρi，μi，νi,(i=1～m)。

表3　众数、中位数、算术平均数

一般情况下，有三种分布特性，右偏分布(ρi<μi<νi)、左偏分布(ρi>μi>νi)、对称分布(ρi=μi=νi)。

4.序列极值与波动特性指标

采用平均离差来反映样本序列的总体变动程度。对表2中的相对数，按照下式(3)计算每个序列的平均离差。对应响应变量，平均离差为：

(3a)

对应于影响变量，平均离差为：

(3b)

由于序列为基于差分的相对数序列，平均离差不仅反映了样本序列综合波动的大小，而且每一个序列的离差在数值上具有可比性，也在一定程度上体现了不同序列之间的波动相关性特征。根据离差，偏斜程度可以采用三次中心动差相对数来表示。假设序列中的值具有相等的权重值，则采用下式(4)计算偏度值。响应变量的偏度值为：

(4a)

影响变量的偏度值为：

(4b)

5.序列的特征模式与相关度

现将计算出的众数、中位数、算术平均数、离差及偏度作为序列的特征模式。该五元组特征模式体现了序列的偏向特征、极值特征、均值特征和波动特征。同时，由于事先通过差分及标准化处理，数列本身已经体现了同一序列之间的差分及相对大小特性。将表3及利用式(3)和式(4)得到的计算结果合并成表4，其第1行对应响应变量，第2行到第(m+1)行则为影响变量的响应结果。

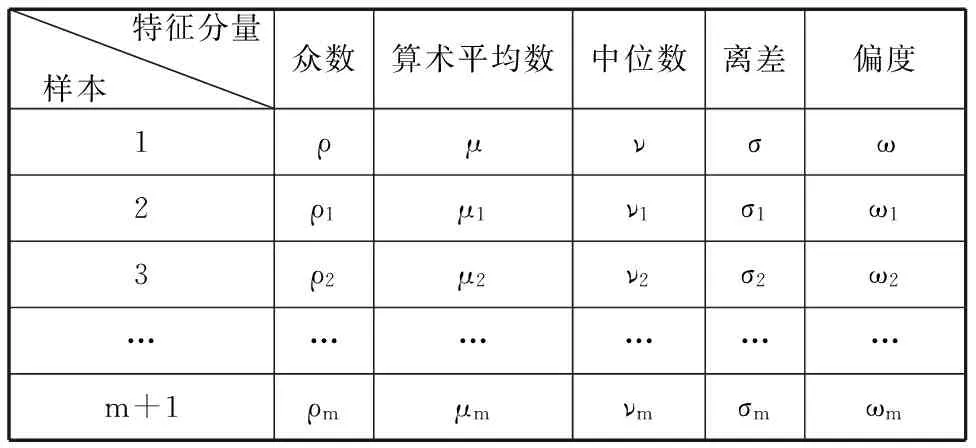
表4　样本的特征值列表

序列的众数、中位数和平均数之间的大小关系反映响应变量与影响变量的同向或异向性，这种偏向特性是相关度的一项重要指标。因此，以算术平均数为中心增加一个方向相关系数，以体现序列偏向的相近程度，定义方向相关系数：

(i=1～m)

(5)

现利用经过改造的欧氏距离计算相关度，其表达式为：

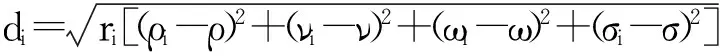
(i=1～m)

(6)

相关度体现了影响变量对响应变量的效用价值。

四、多元回归预测模型

构造如下线性回归模型[6]：

Y=θ0+θ1X1+……+θmXm

(7)

式中，θ0为回归模型的常数项，系数θi(i=1～m)反映了各影响变量对响应变量的影响权重，而相关度反映了各影响变量对响应变量的贡献率。将回归方程的系数表示为：

θi=kdi,(i=1～m)

(8)

其中，k为待定参数。将式(8)代入回归方程(7)，得：

Y=θ0=kd1X1=kd2X2……+kdmXm

(9)

式(9)表明，回归模型的系数估计转换成了求 k之值。利用表1的测量数据并使用最小二乘法，有：[5]

(10)

与表1一致，上式(10)中的yj(j=0～n)为响应变量Y的测量值，xij为影响变量Xi(i=1～m)的测量值。

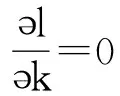
(11)

五、 结　语

系统各因素时变序列中的波动特征蕴涵着各因素之间的相关性，但是在信息效用评价分析过程中，需要克服因素过多、结构复杂等所带来的计算与分析难度。为此本文通过两个层次的变换来获得特征模式。通过序列的差分及标准化获得序列的波动时变序列，使波动相关性分析的数据基础更加客观可靠，也克服了由于数据不同单位、不同大小所带来的问题；在标准化差分序列基础上，将序列的极值特征、平均特征、偏向特征、离差特征、偏态特征作为特征模式构建评价回归模型。由此显著降低信息分析的维数，且由于上述特征在同一序列中具有无关性，因此分析相对更加客观可靠。

[1](美)斯尔太,(美)雷诺兹.信息系统原理[M].张靖，等译.北京:机械工业出版社，2000.

[2]朱晓峰，许发见.论信息资源转换[J].情报科学,2006(3)：331-337.

[3]麻新纯，徐辛酉.基于效用性的历史档案情报价值实现[J].档案学通讯,2010(3):32-35.

[4]Sharanya Eswaran,David Shur and Sunil Samtani.A metric and framework for measuring information utility in mission-oriented networks[J].Pervasive and Mobile Computing,2011,7(4):416-433.

[5]刘红云，骆方.应用心理统计学[M].北京:北京师范大学出版社，2015.

[6]Ronald E Walpole等.概率与统计[M].周勇，等译.北京:机械工业出版社,2014.

责任编校：裴媛慧，孙咏梅

Research on Evaluation Model of Information Utility Based on Timing Correlation

DU Xiao-yan

(Library of Shenzhen University, Shenzhen 518060, China)

The time-related data obtained by processing transaction contain the information with different utility values for supporting prediction and decision-making, and can be used to evaluate utility magnitudes by establishing definite feature patterns. In this paper, the correlations of are analyzed, and the extraction patterns of feature of time series data are studied based on timing and fluctuation characteristics. Built on the difference and relative change of time-varying series, the computation module of correlation degree is constructed between influence variables and response variables by comprehensive utilization of partial state, discrete, correlation, etc..The algorithm reduces the computational complexity ,enhances the reliability of the evaluation, and can be applied to the prediction.

timing characteristics;correlation;feature pattern;information utility；information resource

2016-04-09

杜晓艳，女，江苏新沂人，主要研究方向为图书馆读者服务和学科服务。

G271.4

A

1007-9734(2016)04-0128-04

DOI:10.19327/j.cnki.zuaxb.1007-9734.2016.04.021