基于小波变换和神经网络的卫星钟差预报分析

赵晓阳，黄张裕，杨卫锋，黄　闯，陈梦杰

(河海大学　地球科学与工程学院,江苏 南京 211100)



基于小波变换和神经网络的卫星钟差预报分析

赵晓阳，黄张裕，杨卫锋，黄闯，陈梦杰

(河海大学地球科学与工程学院,江苏 南京 211100)

目前IGS提供的实时钟差精度不够，事后精密钟差也有13 d的延迟，有必要对钟差预报进行研究。文中利用小波神经网络模型进行钟差预报，首先利用小波对原始钟差序列进行分解、降噪，然后利用神经网络进行建模并预报，将得到的结果同灰色模型和二次多项式模型的结果进行对比分析，得出小波神经网络模型可以更好地进行钟差预报的结论。

小波变换；神经网络；卫星钟差；预报

卫星钟作为卫星导航系统的核心部件，是保证卫星导航定位精度的基础和前提，也是影响GPS精密单点定位精度的重要因素。IGS提供的实时钟差不能满足GPS实时精密单点定位的要求，且事后发布的精密钟差也有13 d的延迟。为了满足实时精密单点定位的钟差要求，需要对钟差的预报进行研究。

常用的钟差预报模型有线性模型、二次多项式模型、灰色模型等，但是各方法都有一定的局限性，研究还不够完善。本文结合小波和神经网络进行卫星钟差的预报，该模型结合了小波分析的良好的时频局部化性质及神经网络的自学习功能，因此小波神经网络具有较强的逼近能力及容错能力。将得到的预测序列同灰色模型和二次多项式模型进行对比分析，证明了小波神经网络可以更好的用于钟差的预报。

1　小波分析方法

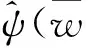
(1)

将ψ(t)称为基小波或母小波函数，将ψ(t)进行伸缩和平移后得

(2)

式中：a为伸缩因子，b为平移因子[5]。

由于ψ(t)生成的ψa,b(t)在小波变换过程中充当小波分析的观测窗口，因此ψ(t)还需要满足以下约束条件[6]。

(3)

(4)

综上所述小波分析与傅里叶分析方法存在差异性，这种差异表现为傅里叶分析方法把时域信号表达成若干精确的各频率分量之和，而小波分析则是将小波变换表示成若干子频带的时域分量之和，因此可进行时频域局部化分析[7]。

2　小波神经网络

小波神经网络(Wavelet Neural Network，WNN)是Rumelhart和McCelland为首的科学家小组在1986年提出的，小波神经网络是小波分析模型与神经网络模型的结合。小波神经网络克服了传统的BP神经网络的缺点，在构建结构和运行速度上都有较大的优势。小波神经网络的结构由输入层、隐含层及输出层组成，假设X1,X2,…,Xk是小波神经网络的输入参数，Y1,Y2,…,Ym代表小波神经网络的预测输出，wij和wjk是小波神经网络的权值。在输入层序列为X1,X2,…,Xk时，隐含层输出为[8-9]

(5)

式中：h(j)为隐含层的第j个节点输出值；wij为输入层和输出层的连接权；bj和aj分别为基函数的伸缩因子和平移因子；hj为小波基函数。

小波神经网络输出层计算式为

(6)

式中：wik为隐含层到输出层的权值;h(i)为隐含层的第i个节点输出值;l为隐含层节点数;m为输出层节点数。

小波神经网络对潮位序列进行预测步的骤流程如图1所示。

图1　小波神经网络流程

3　实例分析

为了分析小波神经网络模型进行钟差预报的精度，本文数据是由IGS提供的2015年6月22日与6月23日两天的间隔为5 min的精密钟差数据，其中前一天的数据是作为建模数据，分别用二次多项式模型、灰色模型和小波神经网络模型来预测第2天的钟差，并将得到的预测数据与IGS提供的精密钟差作比较。同时为了分析预测精度是否与建模数据个数有关，制定4种方案进行实验：

方案1：采用第1天共24 h(即288个历元)钟差数据预报未来12 h钟差；

方案2：采用第1天后12 h(即144个历元)钟差数据预报未来12 h钟差；

方案3：采用第1天后6 h(即72个历元)钟差数据预报未来12 h钟差；

方案4：采用第1天后3 h(即36个历元)钟差数据预报未来12 h钟差；

为了更好的说明小波神经网络模型、灰色模型以及二次多项式模型的预测精度，基于4种方案对这3种预测模型进行比较。WNN表示小波神经网络，GM表示灰色模型，PQ表示二次多项式模型，见表1。

表1　不同建模历元数、不同模型预报统计结果　ns

根据4种不同方案建模，得到的预测精度是不一样的，即3种模型的预测精度随着参与建模历元数的不同而变化。4种不同方案中，灰色模型和小波神经网络模型的预测值和IGS站提供的钟差值都比较接近，在用288个历元建模时，二次多项式模型的预测值和IGS值也接近，但是随着参与建模历元数的减少，二次多项式模型的预测精度急剧下降。对于表1中4种方案，可得出灰色模型和小波神经网络模型对于参与建模的历元数的变化，预测精度并不会急剧下降，但是二次多项式模型的预测精度随着参与建模的历元数的不同变化较大，当参与建模的历元数较少时，可采用灰色模型和小波神经网络模型。

小波神经网络和灰色模型哪一个模型的预测精度更好，对两种模型进行比较。将两种模型得到的预测值分别与IGS提供的精密钟差值进行作差，如图2所示。

图2　灰色模型、小波神经网络模型与IGS精密钟差的差值

由图2可知，小波神经网络模型在建模数据较多时，可以很好的进行学习，所以预测的精度很高，随着建模数据的减少，预测的精度也会随之下降，但并不明显。在图2(a)、(b)、(c)可以看出，灰色模型的预测精度大都差不多，且比小波神经网络模型预测精度差，当建模数据为36个历元时，灰色模型的预测精度下降的较多。在实际预测中，应采用足够多的数据进行建模，可以使预测的精度有一定程度的提高。

4　结束语

由实例分析可知，在建模数据较多的情况下，二次多项式模型、灰色模型和小波神经网络模型的钟差预报精度都很高，可以满足GPS实时定位对钟差的要求。但是随着建模数据的减少，二次多项式模型的预测精度下降的最快，灰色模型次之，当建模数据不够充足时，应尽量避免使用这两种模型。小波神经网络模型可以很好地对钟差进行预报，且精度较高，收敛性较好，但是预报的精度也会随着建模数据的减少而下降。因此，在实际应用中尽可能多的数据建模，从而可以保证预报精度。因此在短期钟差预报中，可以采用小波神经网网络模型进行预报。

[1]王宇谱,吕志平，陈正生，等.卫星钟差预报的小波神经网络算法研究[J].测绘学报,2013,42(3):323-330.

[2]万李,杨杰.小波神经网络在短时交通流量预测中的应用[J].计算机仿真,2012,29(9):352-355.

[3]杨富春,黄张裕,贾莹媛.基于GM(1,1)灰色模型卫星钟差短期预报的精度分析[J].测绘工程,2012,21(5):25-29.

[4]郑作亚,克亚民，卢秀山，等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报,2010,51(1):95-102.[5]黄永红,徐勇.基于小波神经网络的某边坡预测研究[J].测绘工程,2012,21(2):61-63.

[6]郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS钟差预报中的应用研究[J].天文学报，2008，49(3):8-10.[7]崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报(信息科学版),2005，30(5):447-450.

[责任编辑：李铭娜]

Satellite clock error prediction based on wavelet transform and neural network

ZHAO Xiaoyang,HUANG Zhangyu,YANG Weifeng,HUANG Chuang,CHEN Mengjie

(School of Earth Sciences and Engineering, Hohai University, Nanjing 211100,China)

At present, the application of GPS real-time precise single point positioning is more and more popular. However, the accuracy of real-time clock error is not enough, which has 13 days after the precision of the delay, so it is necessary to study the prediction of the clock error. Using wavelet neural network model for prediction of clock error, the paper first uses wavelet to decompose and reduce the original clock sequence. The results are compared with the gray model and the two polynomial model.

wavelet transform; neural network; satellite clock error; prediction

10.19349/j.cnki.issn1006-7949.2016.11.006

2015-09-06

赵晓阳(1991-)，男，硕士研究生.

P228

A

1006-7949(2016)11-0031-03