不同电离层映射函数对导航精度的影响分析

刘　宸， 刘长建 ，叶有龙， 鲍亚东

(信息工程大学 地理空间信息学院，河南 郑州 450001)



不同电离层映射函数对导航精度的影响分析

刘宸， 刘长建 ，叶有龙， 鲍亚东

(信息工程大学 地理空间信息学院，河南 郑州 450001)

介绍广播星历映射函数、投影映射函数、几何映射函数和椭球映射函数4种不同的电离层映射函数，基于Klobuchar电离层模型分析不同电离层映射函数对导航精度的影响。结果表明，不同电离层映射函数对导航精度的影响在厘米级到分米级；在不同太阳活动期，椭球映射函数和几何映射函数对导航精度影响基本相同；在太阳活动活跃期，导航精度由高到低依次为几何映射函数、投影映射函数、广播星历映射函数；在太阳活动平稳期，导航精度由高到低依次为广播星历映射函数、投影映射函数、几何映射函数。建议在导航定位中，电离层映射函数在太阳活动活跃期时采用几何映射函数，在太阳活动低谷期时采用广播星历映射函数。

广播星历映射函数；投影映射函数；几何映射函数；椭球映射函数；导航精度

电离层延迟是卫星导航定位的一项主要误差源。电离层延迟误差在一天内变化几米到二十米不等[1]。显然，电离层延迟必须仔细加以改正。为了组合天顶方向和信号传输路径的TEC，需要映射函数。同时，映射函数还是利用GNSS建立电离层模型的重要因素[2]。但是对于常见的电离层延迟模型的改正精度取决于天顶方向的延迟和投影函数模型的确定精度，而天顶方向的延迟一般确定的比较准确[3-9]。实际中的导航精度要求定位偏差在10m以内，但随着导航定位的广泛应用，导航精度的要求也在不断提高。所以，随着导航精度要求的不断提高以及电离层延迟模型的不断精化，电离层延迟模型映射函数的研究意义更加突出。

电离层映射函数与卫星仰角、卫星方位角、地面站纬度、太阳活动和季节相关[10]。常用的电离层映射函数有：Klobuchar提出的一种适用于GPS的广播星历电离层模型的映射函数[11]；Clynch提出的利用最小二乘方法拟合求解的Q因子映射函数[12]；欧吉坤提出的一种可适用于高度角变化带有侵蚀因子的电离层映射函数[13];StefanSchaer提出的修正单层模型的投影映射函数[14];Sovers，Fanselow提出的双层电离层投影函数[15]等。目前，王一举、刘利、赵晓峰等国内学者对电离层投影函数也作了许多研究[16-18]。本文以Klobuchar模型为电离层模型，研究广播星历映射函数、投影映射函数、几何映射函数和椭球映射函数4种不同的电离层映射函数对导航精度的影响。

1　4种电离层映射函数

利用电离层投影函数F(z)，可实现斜距电离层延迟与垂直电离层延迟的相互转换。电离层投影函数一般视为卫星高度角z的函数，定义为斜距电离层电子含量与垂直电离层电子含量的比值。

(1)

式中：STEC为斜距电离层电子含量；VTEC为垂直电离层电子含量。

1.1投影映射函数

投影映射函数，又称标准单层映射函数，是基于单层电离层模型(SLM)的一种映射函数[14]。单层电离层模型假定自由电子在空间上是均匀分布的，如图1所示，这样等同于所有的自由电子都集中在电离层质心高度(H=350 km )上一个厚度无限小的单层上。投影映射函数可表示为

F(z)=1coszip=11-sin2zip,(2)sinzip=rr+Hsinz.(3)

式中：z为接收机天顶方向和卫星视线的夹角；zip为穿刺点处的卫星天顶角；r为地球的平均半径；H为单层电离层模型的电离层高度。

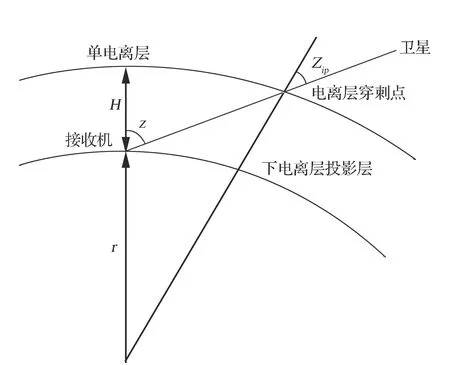
图1　单层电离层模型

1.2广播星历映射函数

广播星历映射函数是标准单层映射函数[11]的一种近似算式，为

(4)

或

(5)

式中：E是卫星高度角(单位：π/rad);h是卫星高度角(单位：rad)。

1.3几何映射函数

假定自由电子的均匀分布与高度相关，那么可以得到几何映射函数为

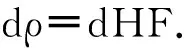
(6)

式中：dρ和dH分别表示电离层路径延迟和天顶延迟。

几何映射函数是基于双层电离层的一种函数，电离层的高度起于50 km止于750 km(见图2)。几何映射函数[15]为

(7)

式中：z为接收机天顶方向和卫星视线的夹角;r为地球的平均半径;ρ为上电离层投影点到视线下电离层投影点之间的距离;H为上电离层投影点到下电离层投影点之间的距离;h为下电离层投影点到地面投影点的距离。当r为常量时，式(4)所得的几何映射函数是球近似。本文中采用r=6 378.137km，H=700km。

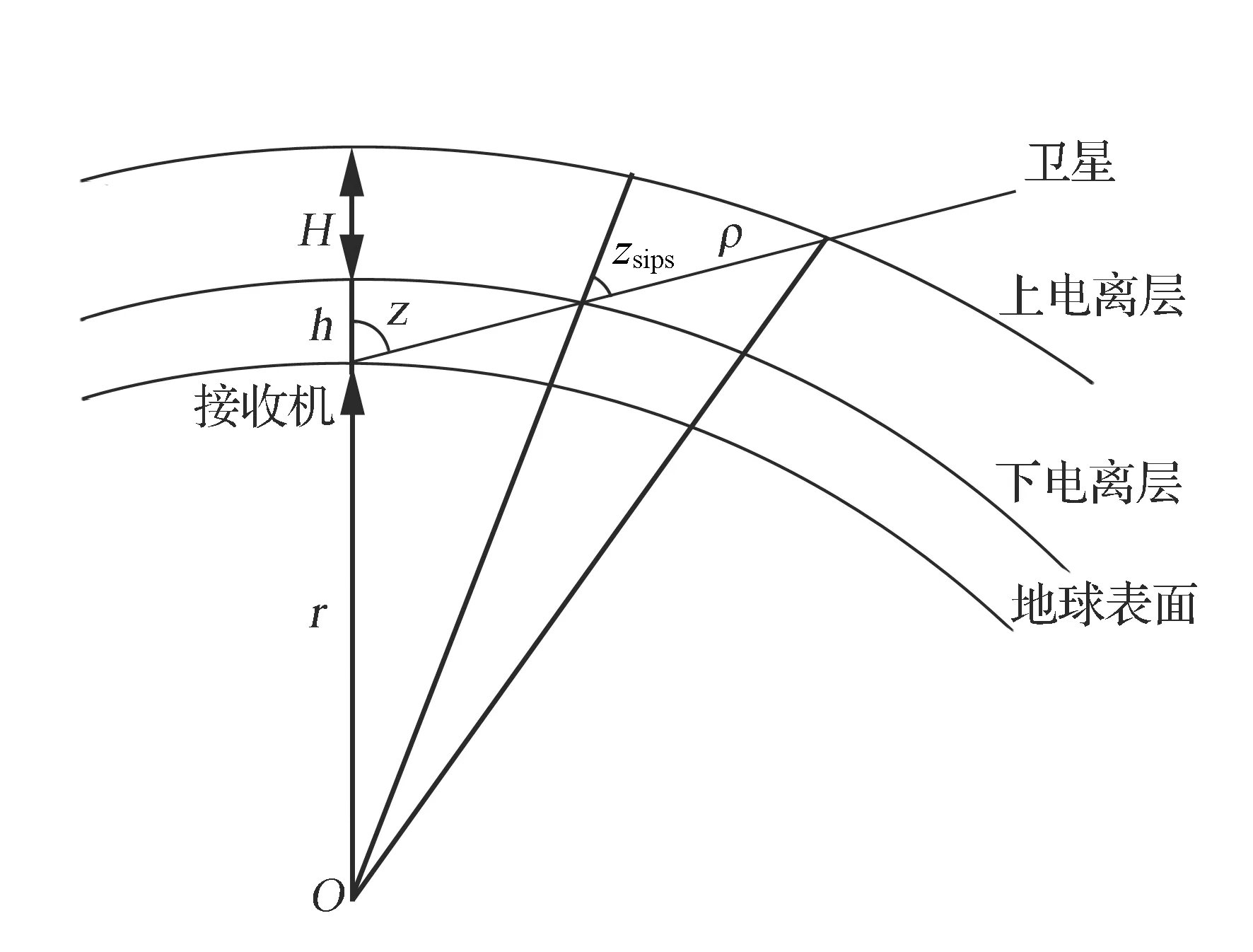
图2　双层电离层模型

1.4椭球映射函数

在几何映射函数中，将r视作一个常量得到的是球近似。当考虑到半径r随着纬度变化的影响时，可以得到椭球映射函数。根据Torge的研究[19]有

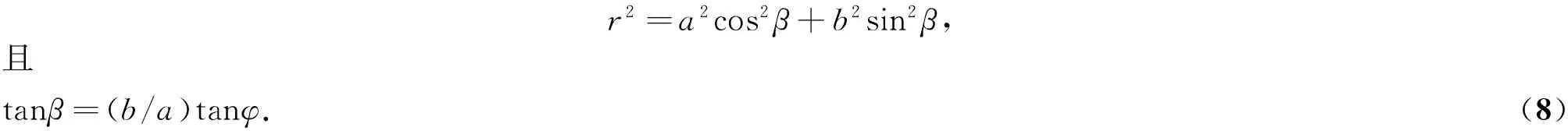
r2=a2cos2β+b2sin2β,且tanβ=(b/a)tanφ.(8)

式中：r为旋转椭球体的半径；a和b分别为旋转椭圆的长短半轴；β为与大地纬度φ有关的角度。通过三角变换可得

(9)

在椭球体的情况下式(7)变为椭球映射函数，即

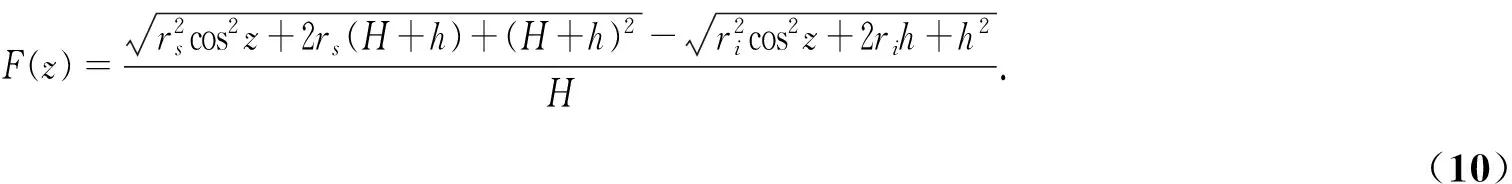
F(z)=r2scos2z+2rs(H+h)+(H+h)2-r2icos2z+2rih+h2H.(10)

式中：rs和ri分别为下电离层投影点和视线下投影点的地心半径。它们可由在式(9)中用φs和φi代替大地纬度φ得到。

2　不同映射函数对导航解的影响

实验所需数据从IGS分析中心CDDIS(Crustal Dynamics Data Information System)官方FTP下载(ftp: //cddis.gsfc.nasa.gov/)[20]。实验基于Klobuchar电离层模型计算的垂向总电离层延迟，分别处理不同太阳活动期单天所有历元在高、中、低纬地区的IGS台站数据，比较不同的电离层映射函数对导航精度的影响，进一步深入评价不同的电离层映射函数。

2.1太阳活动活跃期不同的映射函数的实验分析

在高、中、低纬度地区，分别选取ALRT站(82°29′39.5″N)、ALGO站(45°57′20.9″N)、BOGT站(4°38′24.3″N)3个IGS台站，下载其2015-01-01(太阳活动活跃期)实测数据及相应的广播星历数据，基于Klobuchar电离层模型，利用不同的电离层映射函数，分别进行导航解算并进行统计，比较分析太阳活动活跃期不同电离层映射函数对导航精度的影响，见图3～图5。

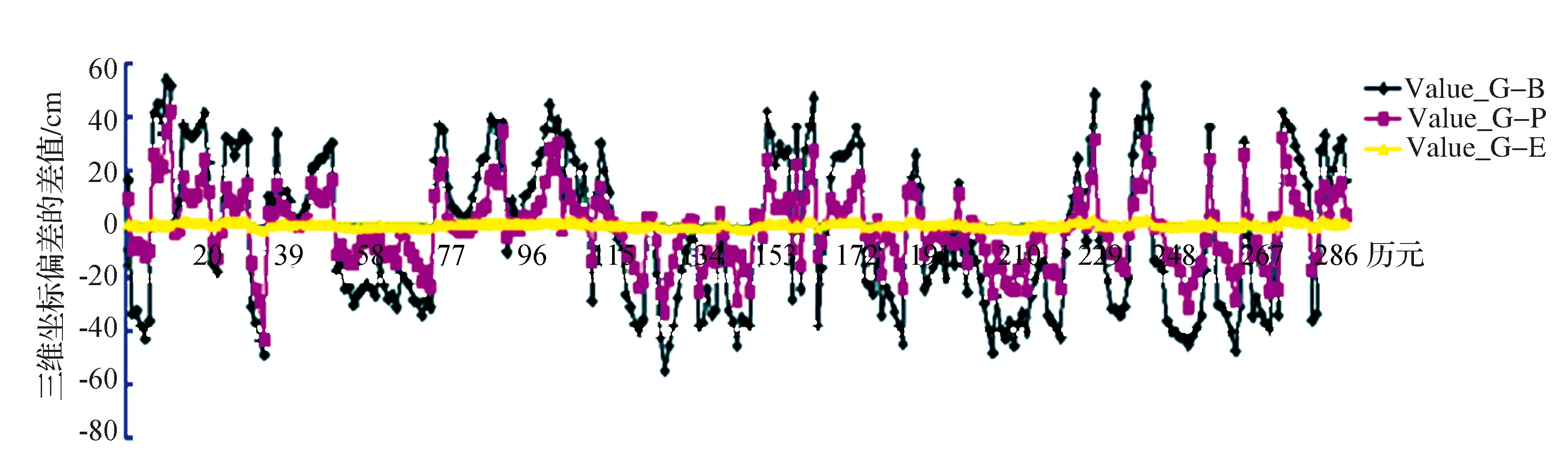
图3　太阳活动活跃期不同映射函数高纬地区(ALRT站)三维导航偏差差值

图4　太阳活动活跃期不同映射函数中纬地区(ALGO站)三维导航偏差差值

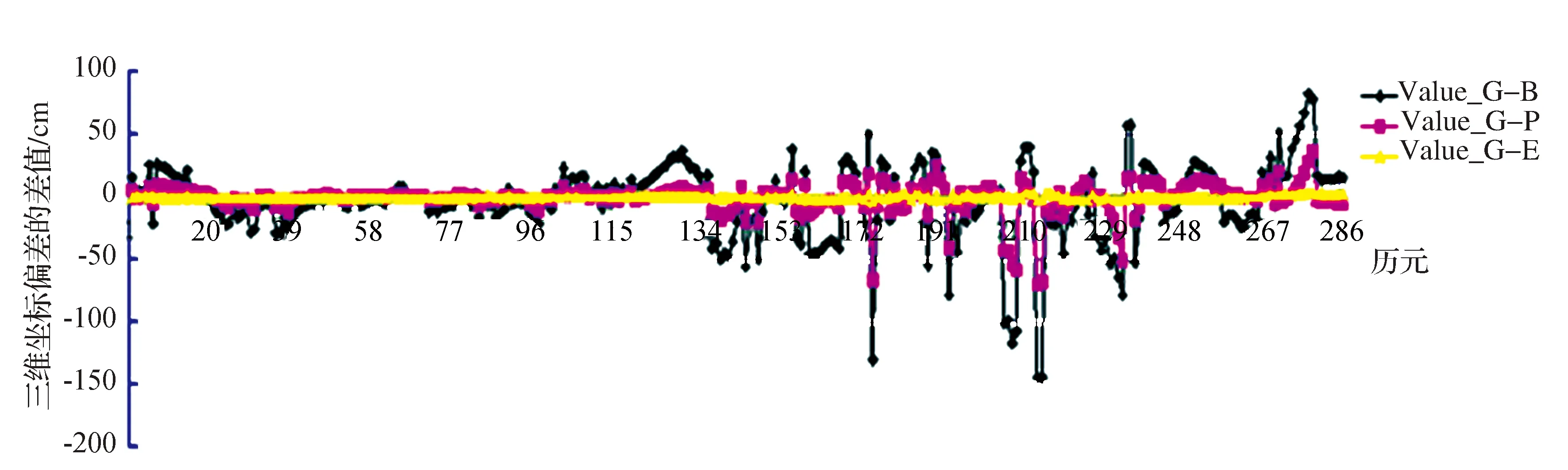
图5　太阳活动活跃期不同映射函数低纬地区(BOGT站)三维导航偏差差值

图3～图5分别表示在2015-04-01历元间隔为5 min的287个历元的高、中、低纬地区采用广播星历映射函数、投影映射函数和椭球映射函数时三维导航偏差与采用几何映射函数时三维导航偏差的差值，其中采用几何映射函数时三维导航偏差为被减数。当差值大于0时，表示前者的三维导航精度优于几何映射函数；反之，则表示前者的三维导航精度劣于几何映射函数。图中，曲线Value_G-B表示采用广播星历映射函数所得差值，曲线Value_G-P则表示采用投影映射函数时的差值，Value_G-E表示采用椭球映射函数时的差值。分析3幅图可知：在高、中、低纬度地区，曲线Value_G-E均在0附近以很小的波动幅度波动；曲线Value_G-B和曲线Value_G-P在0附近以比较大的波动幅度波动。为更直观、准确地反映选择采用不同电离层映射函数时的导航精度，统计各项误差的均方根(RMS)，如表1所示。

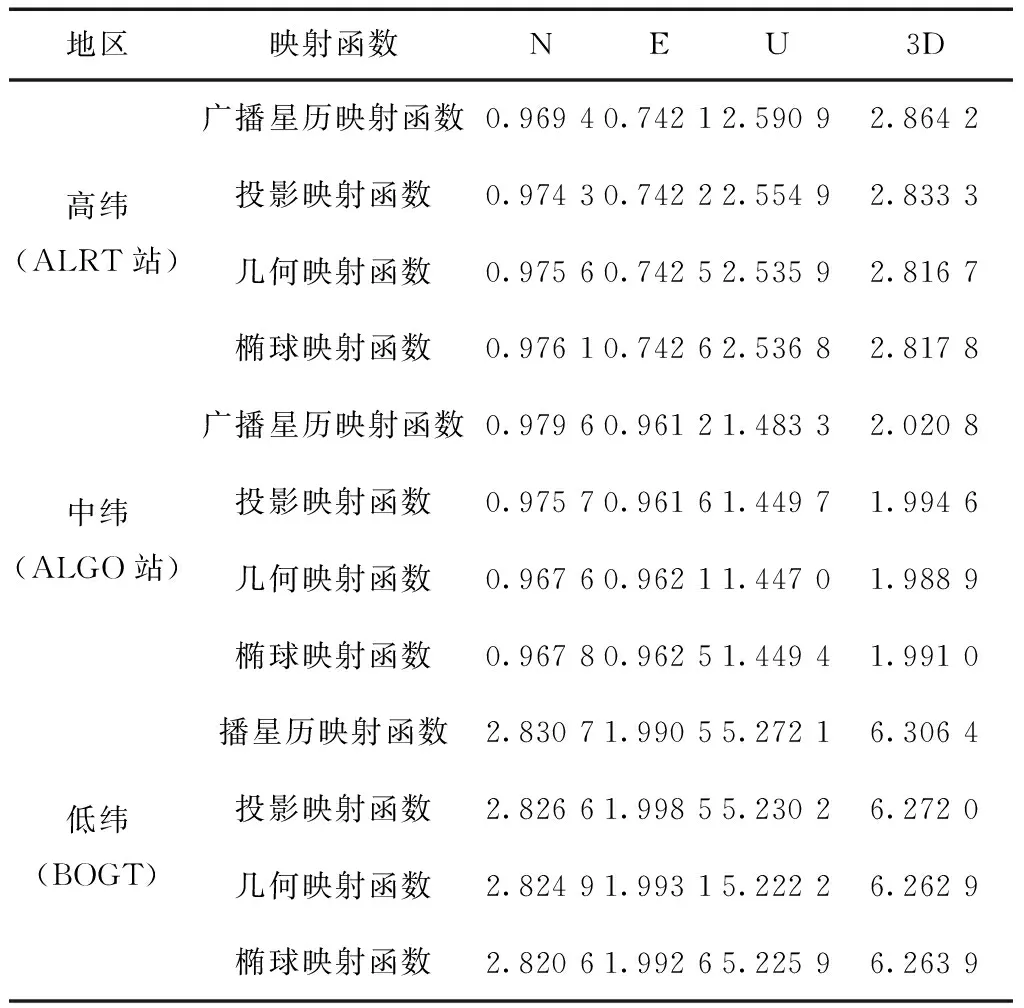
表1　太阳活动活跃年高、中、低纬地区不同映射函数导航误差RMS统计　m

由表1分析可知，基于Klobuchar电离层模型，采用不同映射函数的导航精度中纬地区最高，高纬地区次之，低纬地区最低。不同的映射函数在N(North)、E(East)方向对导航精度没有明显差异，在U(Up)方向有着厘米级的差异：高纬地区采用几何映射函数和采用椭球映射函数的导航精度相当，且比采用投影映射函数和广播星历映射函数时分别高约2 cm和5 cm；中纬地区采用几何映射函数和采用椭球映射函数、投影映射函数的导航精度相当，比采用广播星历映射函数时高约3.5 cm；低纬地区采用几何映射函数和采用椭球映射函数的三维导航精度相当，且比采用投影映射函数和广播星历映射函数时高约1 cm和5 cm。由于不同的映射函数只在U方向对导航精度有影响，不同的映射函数在三维导航精度的影响与在U方向上的影响一致。综合图3～图5和表1可以得出如下结论：太阳活动活跃期时，采用几何映射函数和椭球映射函数的导航精度相当并优于投影映射函数优于广播星历映射函数，且高纬地区的优势最明显，低纬地区次之，中纬地区不太明显。几何映射函数比椭球映射函数计算简单，故建议在太阳活跃期的导航定位中采用几何映射函数作为电离层映射函数。

2.2太阳活动低谷期不同映射函数的实验分析

选取太阳活动低谷期2009-04-01日ALRT站、ALGO站和BOGT站的实测数据及相应的广播星历数据，进行导航解算，与2.1节太阳活动活跃期时相应站点的解算结果作比较，并统计、分析太阳活动低谷期不同电离层模型对导航精度的影响。

图6～图8分别表示在2009-04-01日历元间隔为5 min的287个历元的高、中、低纬地区采用广播星历映射函数、投影映射函数和椭球映射函数时三维导航偏差与采用几何映射函数时三维导航偏差的差值，其中采用几何映射函数时三维导航偏差为被减数。分析3幅图可知：在高、中、低纬度地区，曲线Value_G-E均在0附近以很小的波动幅度波动；曲线Value_G-B和曲线Value_G-P在0上方以比较大的波动幅度波动。为更直观、准确地反映选择采用不同的电离层映射函数的导航精度，统计各项误差的均方根(RMS)，如表2所示。

图6　太阳活动低谷期不同映射函数高纬地区(ALRT站)三维导航偏差差值

图7　太阳活动低谷期不同映射函数中纬地区(ALGO站)三维导航偏差差值

图8　太阳活动低谷期不同映射函数低纬地区(BOGT站)三维导航偏差差值

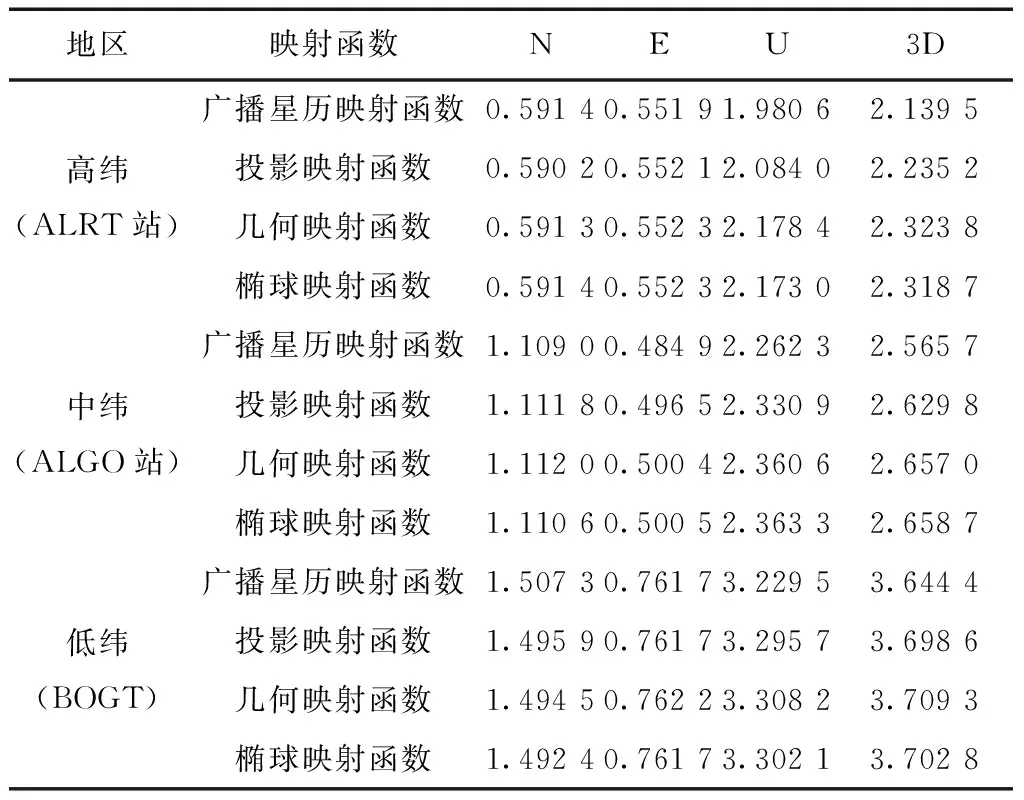
表2　太阳活动平稳年高、中、低纬地区不同映射函数导航误差RMS统计

由表2分析可知，基于Klobuchar电离层模型，采用不同映射函数的导航精度中纬地区最高，高纬地区次之，低纬地区最差。不同的映射函数在N，E方向对导航精度没有明显差异，在U方向的差异在厘米级到分米级：高纬地区采用几何映射函数和采用椭球映射函数的导航精度相当，且比采用投影映射函数和广播星历映射函数时分别低约9 cm和20 cm；中纬地区采用几何映射函数和采用椭球映射函数的导航精度相当，比采用广播星历映射函数和投影映射函数时分别低约3 cm和10 cm；低纬地区采用几何映射函数和采用椭球映射函数的三维导航精度相当，且比采用投影映射函数和广播星历映射函数时低约1 cm和7 cm。由于不同的映射函数只在U方向对导航精度有影响，不同的映射函数在三维导航精度的影响与在U方向上的影响一致。综合图6～图8和表2可以得出与太阳活动活跃期相反的结论：采用几何映射函数和椭球映射函数的三维导航效果相当并劣于投影映射函数劣于广播星历映射函数，且高纬地区的劣势最明显，中纬地区次之，低纬地区不太明显。因此，故建议在太阳活动低谷期的导航定位中采用广播星历映射函数作为电离层映射函数。

3　结束语

本文介绍4种电离层映射函数，包括广播星历映射函数、投影映射函数、几何映射函数和椭球映射函数，并基于Klobuchar电离层模型计算垂直方向的电离层总延迟，进行不同映射函数对导航精度影响的实验。实验结果表明：

1)基于Klobuchar电离层模型进行导航定位时，即使采用不同映射函数，导航精度也满足中纬地区最高，高纬地区次之，低纬地区最差的规律，验证Klobuchar模型更适用于中纬度地区；

2)不同电离层映射函数对N，E方向上的导航精度基本没有影响，主要影响U方向上的导航精度，从而影响三维导航精度；

3)在太阳活动活跃期时，映射函数采用几何映射函数和椭球映射函数时，导航精度优于采用广播星历映射函数和投影映射函数时的导航精度，且高纬度更加明显；

4)在太阳活动低谷期时，映射函数采用广播星历映射函数时，导航精度优于采用几何映射函数、椭球映射函数和投影映射函数时的导航精度，且高纬度更加明显；

5)建议在标准单点定位中，电离层映射函数在太阳活动活跃期时采用几何映射函数，在太阳活动低谷期时采用广播星历映射函数。

[1]许国昌. GPS理论、算法与应用[M]. 北京：清华大学出版社, 2011.

[2]袁运斌. 利用GPS研究电离层延迟的基本原理与方法[D]. 武汉：中国科学院测量与地球物理研究所，2002：46-47.

[3]HOFMANN-WELLENHOF B, LICHTENEGGER H, WASLE E. GNSS-Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More [M]. New York: Springer, 2007: 90-97.[4]黄海莎，刘庆元.震前电离层TEC异常探测方法的研究进展[J].测绘与空间地理信息,2015,38(1): 197-199.[5]李施佳. NeQuick2电离层改正模型的性能评估[J]. 测绘工程, 2015, 24(1):40-43.

[6]刘庆元, 王虎, 王潜心, 等. Galileo改正电离层折射误差高阶项的方法[J]. 测绘工程, 2008, 17(2):9-12.

[7]郑建雷,黄张裕,刘国超.单频精密单点定位中电离层延迟改正方法[J].测绘与空间地理信息,2015,38(2): 44-146.[8]王五魁. IGS电离层VTEC产品内插算法解析[J]. 全球定位系统, 2013, 38(6):17-21.

[9]章红平. 电离层延迟改正模型综述[J]. 天文学进展, 2006, 24(1): 16-26.

[10] RADICELLA S M, NAVA B. Study on the Obliquity Factor Error in Slant to Vertical and Vertical to Slant Ionospheric Delay Conversion[C]. In: Proceedings of the ⅩⅩⅦth URSI General Assembly in Maastricht, 2002.[11] KLOBUCHAR J.A. Ionospheric Time Delay Algorithm for Single Frequency GPS Users[J]. IEEE Transactions on Erospace and Electronic Systems,Vol-aes-23, No.3, May 1987:325-331.

[12] CLYNCH J R, COCO D S, COKER C, et al. A Versatile GPS Ionospheric Monitor: High Latitude Measurements of TEC and Scintillation[C]. In:Proceeding of the ION GPS-98, Colorado Springs, Colorado, USA, 1989: 445450.

[13] OU J K. Atmosphere and Its Effects on GPS Surveying[M]. LGR-Series (14) Delft, The Netherlands: Delft Geodetic Computing Centre, 1996.

[14] SCHAER S.Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System [D]. Bern, Germany: The University of Bern, 1999.

[15] SOVERS O J, FANSELOW J L. Observation Model and Parameter Partials for the JPL VLBI Parameter Estimation Software MASTERFIT-1987[J].NASA STI/Recon Technical Report N, 1987, 88:18423.

[16] 王一举, 袁洪, 万卫星, 等. 低纬地区电离层时延网格算法偏差的研究[J]. 全球定位系统, 2001, 26 (2 ): 5-9.

[17] 刘利, 韩春好. 常见电离层延迟模型投影函数的分析比较[J]. 全球定位系统, 2001, 26(1): 43-45.

[18] 赵晓峰, 李征航. 有关电离层映射函数问题的探讨[J]. 测绘通报, 2003(9): 8-10.

[19] TORGE W. Geodesy [M]. Berlin: Walter de Gruyter, 1991.[20] SANZ J, et al. The ESA/UPC GNSS-Lab Tool (gLAB): an Advanced Educational and Professional Package for GNSS Data Processing and Analysis[J]. NAVITEC 2010 - ESA Workshop on Satellite Navigation Technologies, “5th ESA Workshop on Satellite Navigation User”, Noordwijk, 2010.

[责任编辑：张德福]

The effects on navigation precision: an ionospheric mappingfunction perspective

LIU Chen, LIU Changjian, YE Youlong, BAO Yadong

(SchoolofSurveyingandMappingInformationEngineeringUniversity,Zhengzhou450001,China)

Thispaperintroducesfourdifferentionosphericmappingfunctions,includingbroadcastephemerismappingfunction,projectionmappingfunction,geometricmappingfunctionandellipsoidmappingfunction,andcomparestheireffectsonnavigationprecisionbasedonKlobucharionospheremodel.Theresultsshowthattheeffectonnavigationprecisionvariesfromcentimeter-leveltodecimeter-levelwhendifferentionosphericmappingfunctionsareutilized.Inallsolarperiod,thenavigationprecisionisfundamentallysamewhengeometricmappingfunctionandellipsoidmappingfunctionareutilized.Intheactivesolaractivity,geometricmappingfunctionissuperiortoprojectionmappingfunction,andprojectionmappingfunctionisbetterthanbroadcastephemerismappingfunctioninnavigationprecision.However,inthetroughsolaractivity,broadcastephemerismappingfunctionisthebestonewhenbeingusedinnavigationandpositioning,andprojectionmappingfunctionisbetweenbroadcastephemerismappingfunctionandgeometricmappingfunctioninanavigationprecisionperspective.Therefore,geometricmappingfunctionisadvisedtobeutilizedduringtheactivesolaractivity,whilebroadcastephemerismappingfunctionisadvisedduringthetroughsolaractivity.

broadcastephemerismappingfunction;projectionmappingfunction;geometricmappingfunction;ellipsoidmappingfunction;navigationprecision

10.19349/j.cnki.issn1006-7949.2016.11.005

2015-08-06

国家自然科学基金资助项目(41374041)

刘宸(1991-)，男，硕士研究生.

P228

A

1006-7949(2016)11-0025-06