基于MATLAB语言的变截面无铰拱拱轴线数值优化方法
2016-08-10卓小丽李保军
卓小丽,李保军
(广西交通科学研究院,广西 南宁 530007)
基于MATLAB语言的变截面无铰拱拱轴线数值优化方法
卓小丽,李保军
(广西交通科学研究院,广西南宁530007)
文章以某无支架施工的空腹式变截面特大跨无铰拱为背景,利用MATLAB对拱圈考虑架设过程后的有限元内力计算结果进行分析,并采用三次样条差值函数优化模型对内力结果进行迭代后拟合出最优拱轴线。在拱轴线形优化过程中架设过程对成桥内力的影响最大为8.8%,影响最大的控制截面约在1/8跨径位置;优化后的拱轴线使节点最大压力线偏离量减小了27.8%,且拱轴线与压力线正负偏离值更接近,这样有利于控制截面上下缘对称布筋,提高了经济效益。
变截面;无铰拱;MATLAB;拱轴线;偏离量;数值优化方法
0 引言
拱桥主拱圈轴线的合理选择是拱桥设计中的重要问题之一,陈宝春、肖汝诚等认为大跨径施工的拱桥设计中合理拱轴线优化因桥而异[1]。在设计过程中,由实腹式拱桥恒载分布规律导出的A.Strassner悬链线被较多采用,且荷载分布模式比较常规。周水兴、姜旭东等在拱轴线优化方面研究的内容着重于等截面主拱圈的合理共轴线优化,忽略了施工架设过程中积累的内力变化量[2][3]。然而实际施工过程中,荷载压力线由于荷载分布比较复杂从而难以用简单函数来描述,若通过五点重合法或主拱圈上少数截面逼近恒载压力线,主拱圈上某些非控制截面的压力线可能会与拱轴线的吻合情况不佳,使得主拱圈弯矩过大,从而受力不利。本文的优化方法考虑了架设过程中积累的内力变化量,基于MATLAB语言的强大数值分析功能,实现了三次样条差值作为逼近函数对一座变宽截面拱轴线形进行优化,较人工多次试算的方法提高了效率,且优化效果明显。随着拱桥跨径的不断增大,合理拱轴线的重要性使结构在施工及成桥状态的受力更加突出。
1 工程概况
贵州某采用缆索吊装斜拉扣挂法施工的钢筋混凝土变宽截面拱式渡槽,半跨立面如图1所示。净跨径l0=200 m,矢高f0=40 m,主拱圈采用变宽设计,从拱脚的12 m渐变至拱顶5.5 m,拱圈高度不变。拱圈采用悬链线,拱轴系数m=2.24,拱顶位置设预拱度0.35 m。节点划分时,为了包含常用的五点重合法位置,将拱圈等分后进行单元划分。

图1 渡槽半跨立面图(单位:m)
2 变宽拱圈恒载内力计算
拱圈在进行变截面设计时,为了便于施工,往往仅选择对拱圈宽度或高度其中之一进行变截面设计,本文以较为复杂的变宽进行计算[4]。
2.1变宽拱圈微元形心计算
对于变宽截面拱圈,在变宽拱圈微元ds顺桥方向上近似简化为梯形截面进行形心位置计算(见图2~3):
引入变宽方程b(x)=2ksh(kξ)/(m-1),ξ=2x/l,则有:
A=(a+b)h/2
(1)
将b=2ksh(2k(xi-ds)/l)/(m-1);a=2ksh(2k(xi+ds)/l)/(m-1)代入式(2)积分即可求解形心位置。
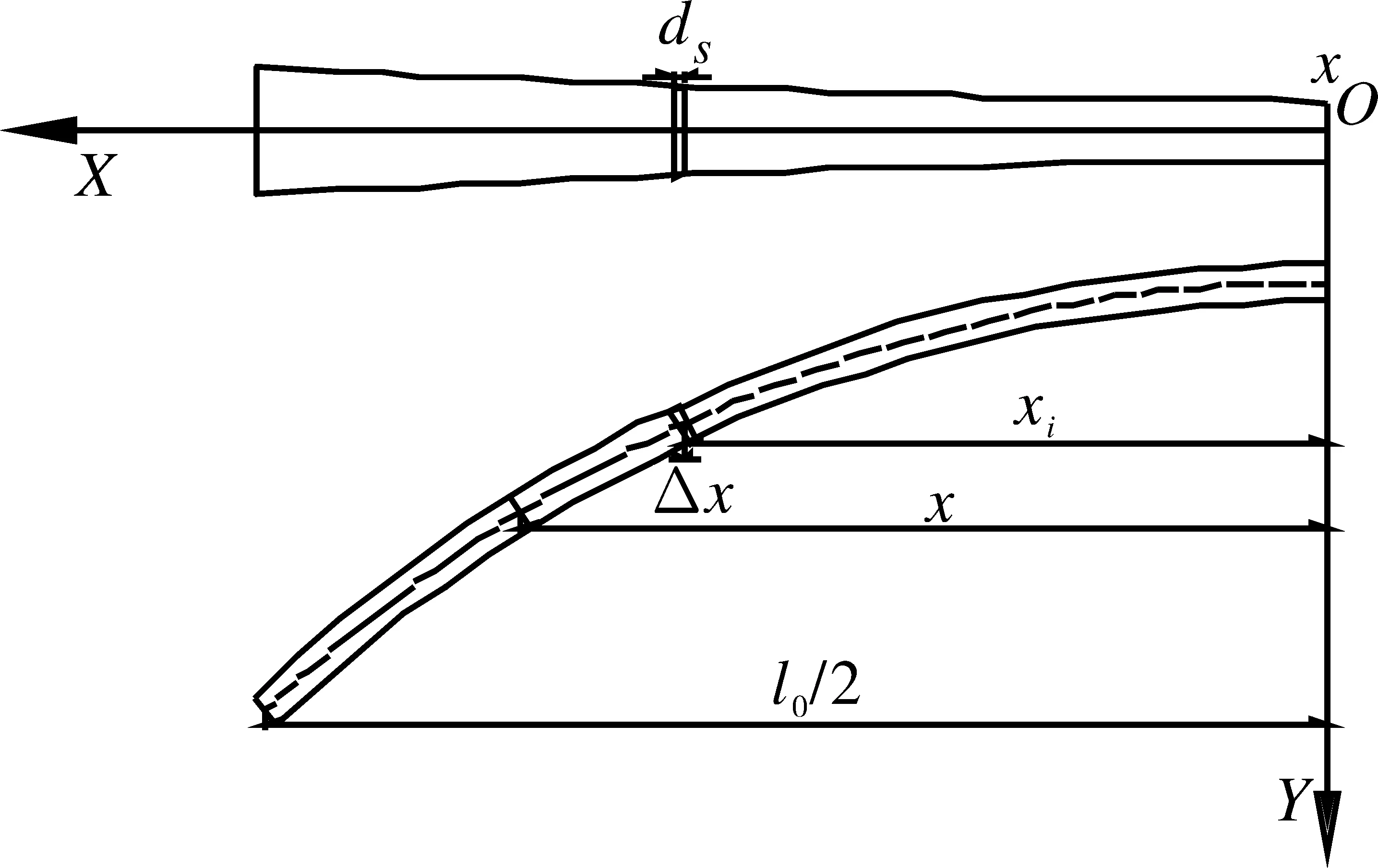
图2 变宽截面主拱圈自重计算图
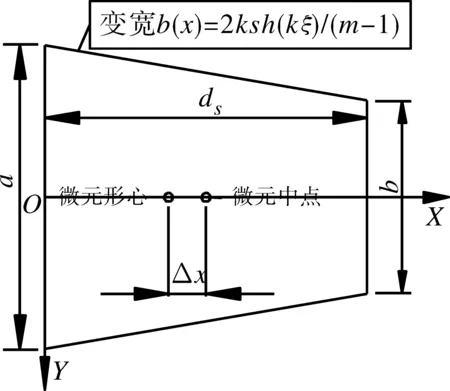
图3 变宽截面微元形心计算图
2.2自重内力计算及变宽截面面积函数

图4 变宽截面面积函数计算图
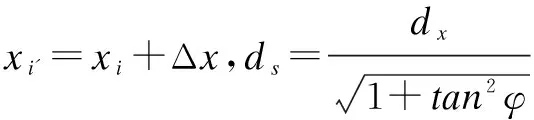
dMi=A(xi)×γ×ds×(x-xi′)
(3)
积分可得:
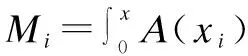
(4)
A(xi′)=2×(bmax-b(xi))N+Amin
(5)
式中:γ——拱圈单位体积容重;
bmax——拱圈设计最大变宽宽度;
Amin——拱圈设计最小变宽宽度对应的横截面面积;
N——拱圈设计顶、底板厚度。
另外,拱圈横隔板重量根据初步设计拟定的坐标采用集中荷载方式考虑。
2.3主拱圈拱上建筑
本工程主拱圈拱上建筑为排架及槽壳,空腹式拱桥分为梁式腹拱及拱式腹拱,集中力作用在主拱圈上是梁式腹拱拱上建筑荷载分配的主要方式。本文研究的工程对象属于梁式腹拱,故以梁式腹拱的拱上建筑为例进行计算分析(见图5)。
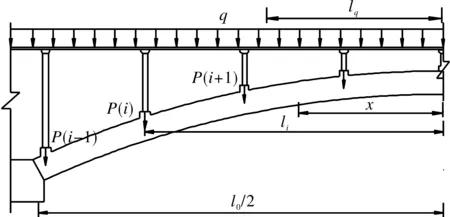
图5 主拱圈拱上建筑计算图
排架墩为集中荷载:
∑MP=∑P(i)·(li-x)
(6)
排架上部结构为均布荷载:
∑Mq=∑q·s·(li-lq/2)
(7)
式中:q——排架上部结构的均布荷载集度;
P(i)——排架墩i的集中荷载,由上式可以计算出拱上建筑对控制截面(拱顶、l0/4、拱脚)或者任意截面的力矩。
3 拱轴线优化的数学模型
3.1三次样条差值函数
拱轴系数优化的方法主要有迭代法、最小二乘法等,分段解析函数法以三次样条差值函数作为恒载压力线的逼近函数较为常用,同样适用变截面拱轴系数的优化,其数学模型为[5]:
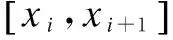
f(x)=aix3+bix2+cix+di,(i=0,1,…,n-1)
(8)
λimi-1+2mi+μimi+1=di(i=0,1,…,n-1)
(9)
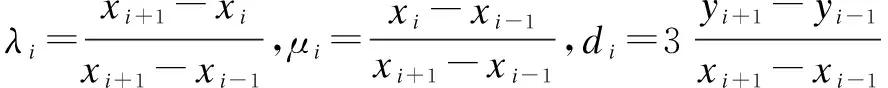
其次,补充边界条件f′(x0)=m0,f′(xn)=mn则式(9)可以确定唯一的m0,m1,…,mn,从而确定了三次样条差值函数f(x)。
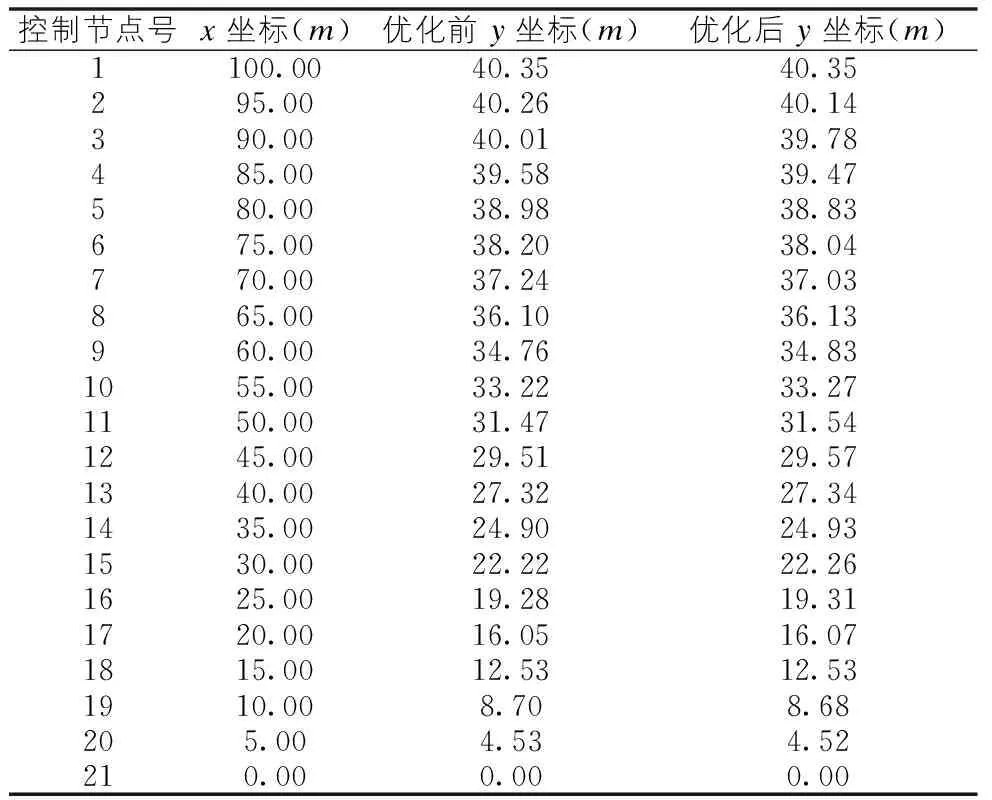
主拱圈的跨径、矢高以及拱上建筑的构造根据桥跨布置即可确定。根据对称性原则,将半跨拱圈分为若干节点0=x0 (10) 求得m0,m1,…,mn后,利用前面介绍的方法计算各单元在节点处的弯矩Mi及轴力Ni(i=0,1,…,n-1),同时结合公式(10)对内节点坐标做如下修正: 3.2计算模型及优化流程 3.2.1计算模型 在进行合理拱轴线优化过程中,其最初的拱轴线是设计拟定的原始轴线。如由于拱圈及拱上建筑是对称结构,取拱轴线的一半为研究对象,拱圈控制节点按半跨拱轴线20等分得到,这样可以包含常用的五点重合法位置,半跨共有21个节点,20个单元[6],见图6。 图6 拱轴线单元、节点划分图 3.2.2优化流程 利用常规的荷载分布模式来求得恒载压力线进而拟合拱轴线这种优化方式,忽略了拱圈分担的荷载与架设过程有关,对大跨径无支架施工拱桥的拱轴线确定影响更大,在拱轴线优化过程中须考虑施工阶段架设过程对成桥状态的影响量,本文以设计拱轴线计算出的施工阶段内力影响量为基础进行优化。 Step1:有限元计算施工阶段对成桥状态的内力影响量; Step2:计算变宽主拱圈及拱上建筑自重对拱圈控制截面内的节点弯矩及轴力; Step3:根据初拟的拱轴线,计算控制点初始坐标; Step4:根据边界条件m0=f′(x0)=(y1-y0)/(x1-x0),mn=f′(xn)=0求解矩阵唯一解m0,m1,…,mn; Step6:输出控制点坐标、拟合拱轴线方程。 由图7分析可知,由于施工过程中的误差累积对主拱圈成桥状态的内力影响不可忽略。对本桥而言,施工阶段对成桥状态的内力(弯矩)影响量最大为8.8%,影响最大的位置约在1/4跨径附近。 图7 施工阶段对k成桥状态内力(弯矩)影响量曲线图 从表1及图8可以看出,按最初拟合的拱轴线在拱脚位置的压力线偏离量较大,在迭代过程中靠近拱脚附近的拱轴线竖直坐标调整相对较大。拱圈轴线优化后使得偏离量更小,在2号控制点位置,最大偏离量比优化前减小了27.6%。拱轴线拟合结果如图9所示。 图8 拱轴线控制节点压力线偏离量优化前后对比图 控制节点号x坐标(m)优化前y坐标(m)优化后y坐标(m)1100.0040.3540.35295.0040.2640.14390.0040.0139.78485.0039.5839.47580.0038.9838.83675.0038.2038.04770.0037.2437.03865.0036.1036.13960.0034.7634.831055.0033.2233.271150.0031.4731.541245.0029.5129.571340.0027.3227.341435.0024.9024.931530.0022.2222.261625.0019.2819.311720.0016.0516.071815.0012.5312.531910.008.708.68205.004.534.52210.000.000.00 图9 三次样条差值拟合结果示意图 本桥在考虑拱圈施工状态转换对成桥内力及线形有直接影响的情况下,根据工程中拱圈变宽、缆索吊装斜拉扣挂的设计及施工特点,采用三次样条差值函数优化模型对内力结果进行迭代后拟合出最优拱轴线,得到如下结论: (1)本文提供了一种利用MATLAB编程工具进行变截面拱轴系数优化的方法,恒载内力的计算精度满足工程需要,与人工试算相比,数值优化方法的效率得到了提高,而且拟合出的拱轴线对比五点重合法更加合理。 (2)本桥拱轴线形优化过程中架设过程对成桥内力的影响最大为8.8%,影响最大的控制截面约在1/8跨径位置,故设计时应充分考虑拱圈施工状态转换过程中内力和线形的变化。 (3)工程优化后的压力线与拱轴线吻合更好,恰当的恒载偏离弯矩可以改善控制截面的内力分布,优化后最大偏离对比优化前减小了27.6%。 (4)优化后的拱轴线与压力线正负偏离值更接近,这样有利于控制截面上下缘对称布筋,提高经济效益。 [1]陈宝春.钢管混凝土拱桥计算理论研究进展[J].土木工程学报,2003(12):47-57. [2]周潇,周水兴.大跨径拱桥计算程序开发与承载力验算方法研究[D].重庆:重庆交通大学,2008. [3]姜旭东,张新胜,等.基于MATLAB语言的拱桥拱肋线形优化设计[J].路基工程,2010(1):67-68,69. [4]杨克鉴,李凤芹,等.大跨度上承式钢管混凝土拱桥设计研究[J].铁道工程学报,2008(12):66-71. [5]石博强,腾贵法.MATLAB数学计算范例教程[M].北京:中国铁道出版社,2004. [6]C.Hu,Y.Wan and X.ShangGuan.A new practice in the design of arch axis[C].Proceedings of ARCH′10-the 6~(th)International Conference on Arch Bridges,2010. Numerical Optimization Methods of Variable-section Hingeless Arch Axis Based on MATLAB Language ZHUO Xiao-li,LI Bao-jun (Guangxi Transportation Research Institute,Nanning,Guangxi,530007) With a hollow variable-sectional super-large span hingeless arch under non-support construc-tion as the background,and through MATLAB,this article analyzed the finite element internal force cal-culation results after arch ring erection considerations,and the cubic spline interpolation function optimization model was used to fit the optimum arch axis after the iteration of internal force results.During the linear optimization of arch axis,the influence of erection process on the internal forces of completed bridge is up to 8.8%,the controlling cross-section with greatest impact is at the position of about 1/8 span;the optimized arch axis can reduce the maximum pressure line deviation of node point by 27.8%,and the arch axis is much closer to the positive and negative offset values of pressure line,which can help control the symmetric rebar layout at the upper and lower edges of control sections,so as to improve economic efficiency. Variable cross-section;Hingeless arch;MATLAB;Arch axis;Discrepancy;Numerical optimi-zation methods 2016-05-12 U448.22 A 10.13282/j.cnki.wccst.2016.06.013 1673-4874(2016)06-0047-05 卓小丽(1989—),硕士,从事桥梁工程设计、科研、试验检测、技术咨询工作; 李保军(1982—),硕士,工程师,从事桥梁工程设计、科研、试验检测、技术咨询工作。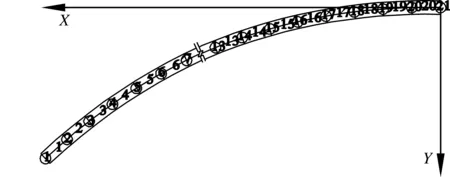
4 优化结果



5 结语
