基于后验概率的低密度奇偶校验码逆向识别方法研究

2016-08-10刘婉月包昕王达金野北京大学信息科学技术学院卫星与无线通信实验室北京100871通信作者Emailwangda2014126com

北京大学学报（自然科学版） 2016年3期

刘婉月　包昕　王达　金野北京大学信息科学技术学院卫星与无线通信实验室北京 100871；通信作者E-mail：wangda_2014@126.com

刘婉月包昕王达†金野
北京大学信息科学技术学院卫星与无线通信实验室北京 100871；† 通信作者E-mail：wangda_2014@126.com

提出一种基于后验概率对数似然比（LLR）均值的逆向识别低密度奇偶校验码（LDPC）校验矩阵的方法。通过估计接收码字的信道增益以及信道噪声方差值得到后验概率对数似然比并依据后验概率对数似然比均值最大化原则成功实现对 LDPC 码校验矩阵的逆向识别。仿真结果表明在加性高斯白噪声信道条件下利用所提出的LDPC码逆向识别技术接收方可准确无误地找到发送方使用的LDPC码校验矩阵。

低密度奇偶校验码（LDPC）；逆向识别；后验概率对数似然比（LLR）

北京大学学报（自然科学版）第52卷第3期 2016年5月

Acta Scientiarum Naturalium Universitatis PekinensisVol. 52No.3（May 2016）doi：10.13209/j.0479-8023.2016.055

低密度奇偶校验码（low density parity check codeLDPC）最早见于 1962 年 Gallager［1］的博士学位论文但是限于当时的仿真条件LDPC码并没有受到应有的重视。1996年Mackay等［2］重新发现LDPC码并指出它与 Turbo码一样具有逼近香农极限的能力。随着对LDPC码研究的深入人们发现其优越的译码性能并将LDPC码应用于更广泛的场景之中。

信道编码盲识别指接收端在对接收信息编码方式未知的条件下实现对接收信息的译码。随着信道编码技术的广泛使用信道编码盲识别的应用越来越多。例如在非协作通信领域可以为接收信息的译码提供可靠的技术支持；在协作通信领域当训练信息不能准确到达时接收端可以对传输信息进行译码；在智能移动通信和多点广播通信领域，当发端采用自适应编码时接收端可以对信号内容进行识别和利用。

目前国内外学者对线性码提出几种盲识别方案。针对线性分组码Valembois［3］归纳为联合判决问题提出基于校验向量的二元线性分组码的盲识别方法；Mathieu［4］基于 Valembois 的思想通过生成一系列低码重的码字来实现迭代译码实现码长较短且误码率低的线性分组码的盲识别。上述两种方法在LDPC码长未知且码字起点未同步的情况下并不适用。

针对未删除卷积码，有学者提出基于快速何冲算法［5］的盲识别方法和基于欧几里得算法的盲识别［6］。针对删除的卷积码有学者提出基于生成多项式的盲识别方法和基于校验矩阵与生成矩阵正交关系的盲识别方法［7-8］。上述方法在 LDPC 码字序列的起始位置未知时并不适用且计算量巨大。

可见已有的研究方法虽然对 LDPC 码盲识别研究有一定的借鉴意义但不能解决在码长未知且起点未知的情况下的逆向识别并且计算繁复。

本文利用校验关系和后验概率的对数似然比，对LDPC码逆向识别技术进行研究提出一种基于后验概率对数似然比（log likelihood ratioLLR）均值判断校验矩阵的方法。我们假设接收到的信号样本在统计学意义上彼此独立通过期望值最大算法［9］（expectation-maximization algorithmEM）对噪声参数进行预测并确定合理的LLR均值判断阈值实现码字起始位置的准确识别并从可选的LDPC码校验矩阵集合中找到发送方编码所使用的LDPC码校验矩阵。

1　基于后验概率LLR的LDPC码逆向识别算法原理

每一种 LDPC码有唯一的校验矩阵因此如果将校验矩阵与接收码字建立关系就能够明确地找到编码使用的校验矩阵 θ。本文首先计算 LLR，然后计算每个校验矩阵对应的平均 LLR以此为依据选择编码矩阵。

1.1 对数似然比

即为 X取值为 0和 1概率比值的自然对数。对于给定的另外一个随机变量 YX关于 Y的条件对数似然比可以表示为

根据贝叶斯公式可以得到以下关系式：

1.2 LLR在LDPC码逆向识别中的应用

从编码器集合 Θ 中选择θ ′可以确切地知道此编码器对应的校验矩阵，

其中 n 表示码字码长k 表示信息位个数。由校验关系可知，=0当且仅当θ ′=θ 时成立其中表示发送端由校验矩阵 Hθ编码得到的第 v 个 LDPC 码字0是（n-k）×1的零向量［9］。

表示校验矩阵θ′H第 i行非零元素的位置Ni表示第 i行非零元素的总数。LDPC码字表示为vθ= c ［cv，0cv，1…cv，n-1］T因此校验关系可以表示为，当且仅当θ ′=θ 时成立。

对于LDPC码本文假设各发送信息的码元是统计学意义上独立同分布的。由于这一性质接收到的信号的码元也相互独立。因此有

其中yv表示接收端收到的LDPC的码字。

由于LDPC码字中各码元取0和1的概率相同因而发送端信息码元的后验概率对数似然比为0。我们计算Hθ′中第 i 个校验关系对于第 v 个码字的后验概率的对数似然比率公式如下：

根据对数似然比的定义以及校验关系可知：当θ ′=θ 时对数似然比率一定为正对所有校验位的后验概率的对数似然比求平均取值也一定为正；当θ ′≠θ 时每个校验位的后验概率对数似然比的正负是不确定的所以对所有校验位的后验概率LLR进行平均值运算时数值之间会相互抵消。

接收到的第v个码字的平均LLR可以表示为

不同的校验矩阵有不同的 n 和 k 值因此n-k （即校验位的个数）的值显然是不同的。对编码矩阵的选择可以表示为因此需要对编码矩阵集合中的所有校验矩阵进行计算。

为了加速逆向识别过程本文对前 h个校验位计算平均 LLR值如果此时可以判断出编码矩阵，则停止对其后的校验关系的计算；如果无法判断，则再计算累加h个校验关系的平均LLR值。

通过对校验矩阵集合中每一个校验矩阵的平均LLR 值的计算选择使得平均 LLR 值最大的校验矩阵为信息编码矩阵实现对 LDPC 码的闭集逆向识别。

2　基于后验概率LLR的LDPC码逆向识别算法实现

从 LLR 计算公式可知需要知道信道对发送信号的影响（包括幅度增益和噪声功率）因而首先对接收信号中信道的影响进行估计。在仿真时假设码长和码字起点未知需要设计逆向搜程序找寻码字起始位置。由于判决时选择 LLR 均值作为指标因而需要选取阈值作为判断标准当 LLR 均值大于阈值时认为此时进行判决的校验矩阵即为接收信息对应的正确矩阵。

2.1 EM算法对信道参数预测

EM 算法［10］中定义接收信息 y 是不完整数据，完整数据定义为cd=［yTaT］T即获得的接收数据y以及各接收数据的正负符号组成的向量 a［10］。用Q（θi；θi-1）表示完整数据的似然函数的期望其中参数向量值θi与在接收信息y条件下的完整数据以及θi-1相关。

在此算法第 i次迭代中参数 θi即为使得上述期望公式最大的值：

直到特定条件EM 算法会收敛到似然函数的一个极大值。

期望公式的推导如下：

其中 C是常数。定义第 n个信息位由在接收到的信息和第（i-1）次迭代参数向量计算出的期望值为

带入Q的表达式中得到参数表达式：

最后得到的预测结果为

I是最终迭代次数由迭代终止条件决定。

对上述预测结果的偏差进行处理其结果的表达式为

利用 EM 迭代方法可以获得接收信号的幅度与噪声方差的预测值即

2.2 仿真选码准则

LDPC码具有近香农极限的误码性能、无错误平层、译码速度快等优点，但其校验矩阵具有随机性编码较为复杂。QC-LDPC码是一种基于几何构造的LDPC码，继承了LDPC码的优点同时降低了编译码复杂度，可实现性强，被 IEEE802.11n （WLAN）IEEE802.16e（WiMAX）和 CCSDS 等多个通信标准采用，实际上，常用的 LDPC 码多为 QCLDPC 码或其变种。本文选用 QC-LDPC 码进行仿真，选择的 2016 码长和 1008 码长的 QC-LDPC 码的校验矩阵（均经密度推演算法优化）具有代表性和常用性。备选校验矩阵中的部分 QC-LDPC 校验矩阵在加性高斯白噪声信道（AWGN）下的误码性能如图1所示。

2.3 判断阈值的确定

根据逆向识别原理可知，当被检测的校验矩阵即为编码所用的校验矩阵时，利用接收到的 LDPC码计算得到的平均 LLR 值一定为正；当被检测的校验矩阵不是编码所用的校验矩阵时，单个校验方程计算的 LLR 值可正可负，因此所有校验方程计算的均值 LLR 也可正可负。为了区分上述两种情况（平均 LLR 都为正），本文设定一个判决阈值。当平均LLR大于判决阈值时，认为当前被检测的校验矩阵即为发送端产生 LDPC 码所使用的，反之，则放弃这个校验矩阵，对下一个校验矩阵进行检验［9-10］。

对上述阈值的选择采用仿真来确定。仿真条件是，在信噪比为-2dB时，对2016码长、5/8码率的LDPC码在每一个阈值仿真200次，统计选择起始位置正确的概率结果如表1所示。

从图 2可以看出，当阈值在 29～35之间时，起点判断正确率为100%。当阈值设定小于29时，由于阈值较小，非对应的校验矩阵的均值LLR也有可能会超过阈值，造成起点判断错误。当阈值选择过大，如大于35时，不仅非对应的校验矩阵的均值上相同。实际应用中，不能因为信噪比的变化以及校验矩阵的不同而改变阈值，所以阈值与起点选择准确率关系的稳定性很重要。LLR无法超过阈值，对应的校验矩阵也可能小于阈值，造成无法选择出起点位置，使得起点选择的准确率降低。

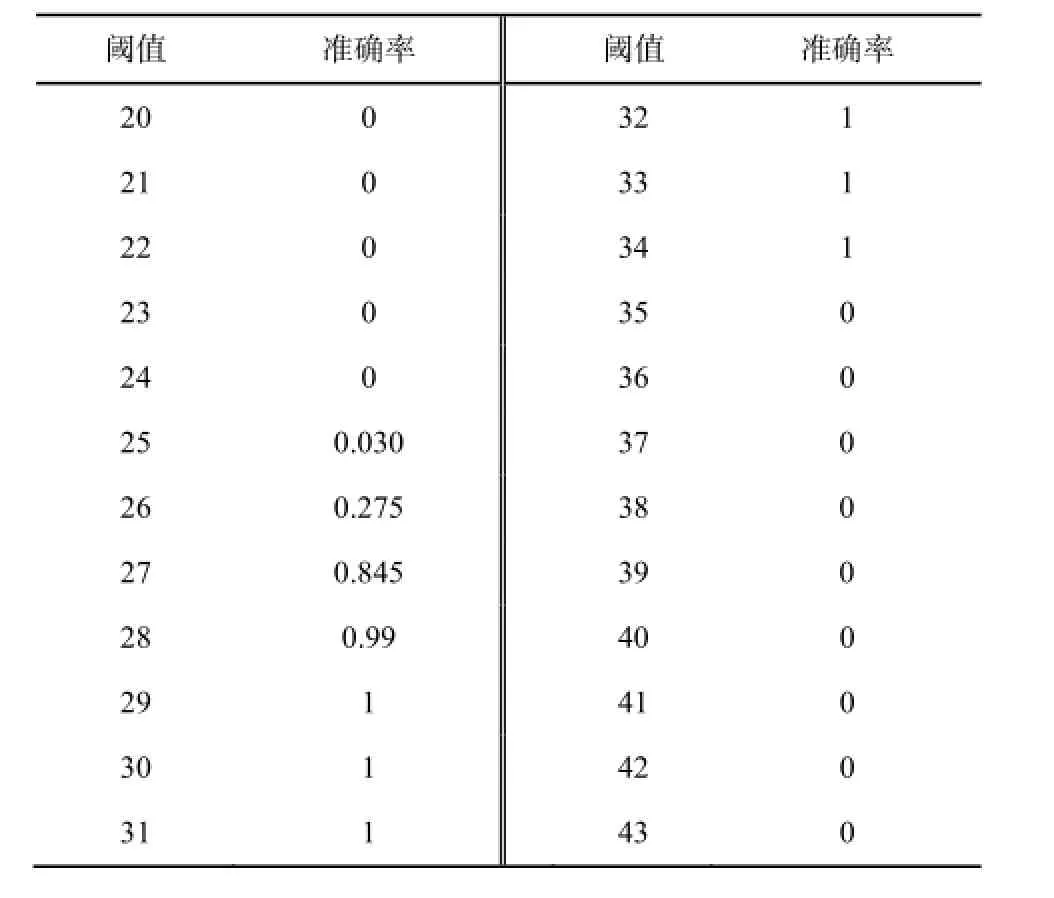
表1　2016码长的LDPC码阈值–起点选择准确率仿真结果Table1 Simulation results of threshold with LDPC code length of 2016

表2　1008码长LDPC码阈值–起点选择准确率仿真结果Table 2 Simulation results of threshold with LDPC code length of 1008

表 2 和图3为在 -2 dB 信噪比下，对 1/2 码率、1008码长LDPC码阈值确定的仿真结果。

对2016码长和1008码长的QC-LDPC，分别在信噪比为6和-2dB的起点选择准确率与阈值关系进行仿真，结果如图4所示。

从图4和5的仿真结果可以看出，对于备选集合中的LDPC码的校验矩阵其起点选择准确率与阈值的关系在信噪比［-26］dB 范围内的变化基本

2.4 逆向盲搜程序设计

接收端对收到的信息进行逆向识别前，需要设计逆向盲搜程序来确定码字的起始位置。

逆向盲搜程序的设计原则与逆向识别原则相同，都依赖于每个 LDPC 独特的校验关系。如果LDPC 码与校验矩阵匹配，则校验码的平均后验概率 LLR 为正，本文设定了阈值，当均值 LLR 大于此阈值时，认为LDPC码与校验矩阵匹配。

基于这一原则，以第一个码元为起点，取连续n测LDPC，将其与给定的校验矩阵集中的每一个校验矩阵进行运算，计算平均LLR值。如果LLR值大于给定的判定阈值，即认为该LDPC码的第一个码元的位置为码字的起始位置；否则，以第二个码元为起点，重复上述步骤。依此递推，计算得到接收信号中码字的起点。

为了验证找到的起点的正确性，仿真时发送端连续发送多个 LDPC 码字（这样仿真是合理的因为在实际通信中需要传输大量的信息，因而传输的码字一定不只一个）。本文认为在一次传输中采用同一个校验矩阵生成 LDPC 码。在可能的起点后，连续取 5个 LDPC 码进行逆向识别检验。如果这些码字逆向识别得出的校验矩阵都相同，则认为起点选择准确；如果不完全相同，则认为起点选择错误，从该起点的下一比特开始重新搜索。闭集逆向识别程序设计如图6所示。

3 仿真分析

本文对码长为2016bit的LDPC码进行仿真。备选矩阵集中，2016码长矩阵有7个（码率为1/4、3/8、1/2、5/8、7/8的矩阵各1个，码率为3/4的矩阵有两个）；码长为1008的矩阵1个（码率为1/2），即闭集集合规模为 8。加入不同码长的校验矩阵实现未知码长条件下的闭集识别在逆向识别中将阈值定为33。

仿真结果如表 3～5 所示其中SNR为信噪比，Ber为误比特率，Suc_r 为逆向识别准确率。

从表 3～5可以看出当阈值为 33时，发送方无论选取何种码率的 LDPC 码进行编码，无论新信道质量好坏接收方均可以 100%准确地判断发送方所使用的 LDPC 码校验矩阵，因此，逆向识别准确率可以达到100%。

4　结论

本文对 LDPC 码逆向识别技术进行研究利用后验概率 LLR 的均值对接收到的 LDPC 码字的校验矩阵进行逆向识别。通过对接收信噪比进行估计实现对接收码字的信道增益以及信道噪声方差值的估计得到计算后验概率 LLR 所需要的信道增益和噪声功率的估计值。通过盲搜程序实现对码字起始位置的查找。依据后验概率 LLR 均值最大化原则成功实现对 LDPC 码字的逆向识别。本文对在不同阈值下校验矩阵和码字起点确定的准确率进行仿真确定最优阈值提高了盲识别判决准确率。仿真结果表明在最优阈值下接收方可以利用本文提出的 LDPC 码逆向识别技术准确无误地实现LDPC码校验矩阵的闭集逆向识别。

表3　LDPC码码率为3/8时仿真结果Table3Simulation results of LDPC code rate being 3/8

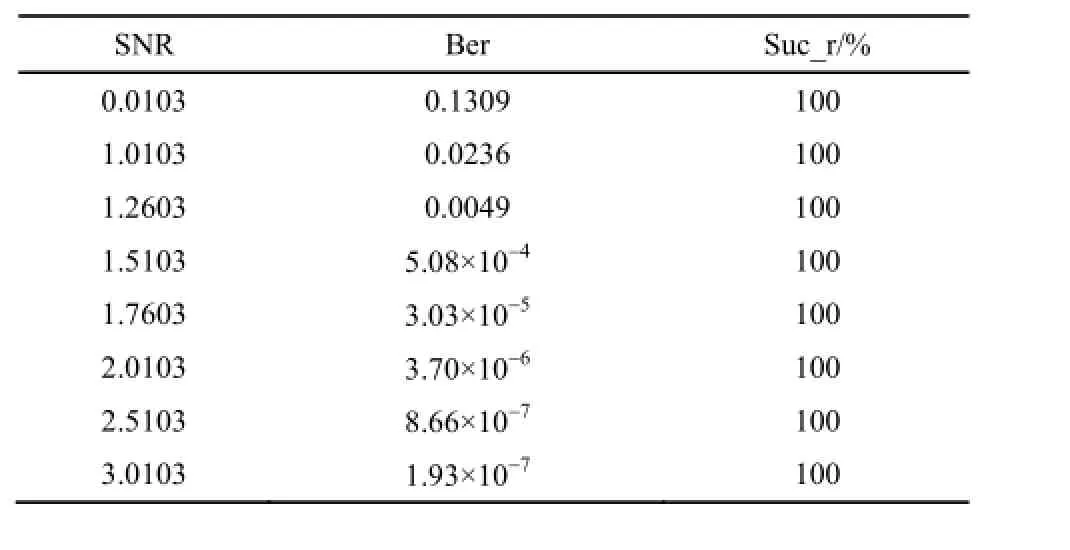
表4　LDPC码码率为1/2时仿真结果Table4 Simulation results of LDPC code rate being 1/2

表5　LDPC码码率为5/8时仿真结果Table5 Simulation results of LDPC code rate being 5/8

［1］ Gallager R G. Low-density parity-check codes. IRE Trans Info Theory19628（1）：21-28

［2］ MacKay D J CNeal R M. Near Shannon limit performance of low-density parity-check codes. Electron Lett199632：1645-1646

［3］ Valembois A. Detection and recognition of a binary linear code. Discrete Applied Mathematics2001111：199-218

［4］ Mathieu C. Block code reconstruction using interative decoding techniques // IEEE International Synmposium on Information Theory. Seattle2066：2269-2273

［5］ Lu P ZZou Y. Fast computation of Grobner basis of homogenous ideals of F［xy］. Science in China：Ser F200851（4）：368-380

［6］邹艳陆佩忠. 关键方程的新推广. 计算机学报，200629（5）：712-718

［7］柴先明黄知涛王丰华. 信道编码盲识别问题研究. 通信对抗2008（2）：33-36

［8］黄知涛柴先明陆凤波等. 一种（n-1）/n码率的删除卷积码的盲识别方法：中国CN200810030735.3［P］. 2008

［9］ Wiesel AGoldberg JMesser H. Non-data-aided signal-to noise-ratio estimation // IEEE Proc IEEE International Conference on Communications. New York2002：197-201

［10］ Tian XWu H C. Novel blind identification of LDPC codes using average LLR of syndrome a probability. IEEE 12th International Conference on ITS Elecommunications201262（3）：632-640

Research on Low Density Parity Check Code Reverse Recognition Methods Based on Posterior Probability

LIU WanyueBAO XinWANG Da†JIN Ye
Satellite and Wireless Communication LaboratorySchool of Electronics and Computer SciencePeking University，Beijing 100871；† Corresponding authorE-mail：wangda_2014@126.com

This paper presents a method of the reverse recognition of the check matrix coded by low density parity check code （LDPC）which is based on the posterior probability log likelihood ration （LLR）. The posterior probability LLR was obtained by estimating the channel amplification and the variance of the noise in the received code. A reverse recognition of LDPC code check matrix was achieved following the LLR mean value maximization principle. Simulation results show that the receiver can precisely retrieve the LDPC check code used by the sender under different channel circumstances through the LDPC reverse recognition method.

low density parity check code （LDPC）；reverse recognition；posterior probability log likelihood ration （LLR）

TN911

2014-12-16；

2015-07-28；网络出版日期：2016-05-17