一种改进的RBF神经网络对县级政府编制预测

刘道华,张 飞,张言言

(信阳师范学院 计算机与信息技术学院,河南 信阳464000)

0 引言

编制的核定是一个较为重要且复杂的行政工作，许多下级编办为了更多地争取政府人力资源及财政转移支付资金，向上级编办超量申请编制.因此，研究如何运用预测的方法，为各级编办在进行编制决策时提供科学合理的依据，具有十分重要的意义.常见的编制预测方法主要有经验分析法、灰色预测方法等.例如,祝红军[1]以X市政府办公厅为例进行分析，建立了灰色预测模型，对公共部门人力资源的灰色预测方法进行了探究；李丙红[2]采用主成分分析方法对我国省级政府人力规模进行了综合评价；杨小斌[3]采用趋势回归法、组合预测法对江西省公共事业编制规模进行了预测.这些学者对编制预测方面的探索均取得了一定的研究成果，在一定程度上提高了编制决策的科学性和准确性.对于经验分析法，由于目前政府管理的新形势，在政府机构改革快速推进的新时期，该方法已无法满足当今编制总量的预测.而灰色预测方法主要侧重于时序预测，其所建立的模型是依据控制论的相关理论所构造的微分方程，并不能较好地反映出预测对象的特点.因此，本文引入了RBF神经网络对编制总量进行预测.RBF网络为三层前馈神经网络，具有结构简单、无局部极小点、计算过程简洁、训练学习的收敛速度快等优点.但是，RBF网络大多需要根据经验学习来确定函数中心宽度这一参数.本文提出了一种改进的RBF网络算法，通过引入GCV准则进一步优化宽度参数σ；同时，对RBF网络进行子网络化优化处理，规避在高阶矩阵对角化和求逆过程中出现超大计算量.

1 径向基函数神经网络

RBF(Radial Basis Function)网络起源于数值分析中多变量插值的径向基函数方法.RBF网络具有比BP神经网络更加简单的结构，并且无局部极小点，计算过程更加简洁，训练学习的收敛速度快3至4个数量级，因此应用也更加广泛[4-5].RBF网络由输入、隐层和输出三层构成，即为三层前馈神经网络[6].

常见的RBF网络算法有序贯学习和批处理学习两类算法[7].序贯学习算法是为了解决利用RBF网络实现在线预测的需求，该算法与批处理学习算法的不同之处在于，该算法对训练样本不存在先验知识，在网络学习、确定结构和参数时，一次输入一个训练样本.常见的序贯学习算法有：M-RAN(最小资源分配算法)、RAN(资源分配网络算法)等[8].和序贯学习算法不同，批处理学习算法需要在已知全部训练样本的情况下，首先学习训练全部样本，设定网络误差的阈值，然后不断分析学习后的输出误差并相应地调整网络参数，循环迭代此过程，当达到设定阈值时完成训练学习过程[9-10].常见的批处理学习算法有：梯度下降法、正交最小二乘法、k均值聚类算法等[11-12].

2 改进的RBF网络算法

RBF网络大多需要根据经验学习确定函数中心宽度σ.改进的RBF网络算法的具体步骤：

Step0：对采集的原始数据标准化处理；

Step1：将数据样本分成2类；

Step2：对第一类数据利用正交最小二乘学习确定RBF网络各隐含层节点的数据中心和其他参数，采用GCV准则进行参数的优化.具体步骤如下.

③用伪逆方法计算网络的输出权值，并得到此时样本的输出误差，采用

(1)

定义网络训练误差为均方根误差，如果rssk<ε，则停止矩阵选择P的列向量.

⑥重复以上步骤，直至找到X个数据中心，使网络的训练误差小于给定误差ε.

⑦采用

(2)

作为GCV准则进行参数的优化.

通过训练学习，分析不同的中心宽度σ对应的GCV准则值，寻找GCV的极小值，并最终确定GCV有极小值时对应的基函数中心宽度值σ.

Step3：求解权值；

Step4：对第二类数据执行Step2—Step3；

Step5：采用

(3)

对子网络整合；

Step6：采用

(4)

得到子网络的预测，对2个子网络的输出按照下式

(5)

做加权和整合，得到整个RBF网络的预测值.

3 基于改进的RBF网络算法对某县区政府编制总量预测

3.1 采集编制核定相关指标的原始数据

对于编制总量的预测，可以从反映政府管理工作总量和管理幅度的相关指标因素来分析，也可以从经济指标等方面进行考虑.尤其是地方政府，其管理辖区的地域面积、生产总值、辖区内人口总量、财政收入总量、政府财力水平等因素都可以纳入到编制总量预测的指标体系中.本文选取如下指标作为预测变量：TZ代表年份；X1代表人口规模(人)；X2代表经济水平(万元)；X3代表地域面积(平方公里)；X4代表财政收入(亿元)；X5代表民间非政府组织(个)；X5-1代表社会组织；X5-2代表民办非企业；X6代表公职人员年龄占比分布；X6-1代表50岁以下；X6-2代表50岁以上；X7代表公职人员学历占比分布；X7-1代表研究生及以上；X7-2代表本专科；X7-3代表专科以下.

本文各编制核定相关指标基础数据源于某县区统计局及其发布的历年《某县区国民经济和社会发展统计公报》、该县区地方志及其编撰的历年《某县区年鉴》、该县区档案馆藏资料、该县区机构编制委员会办公室内部资料[13].对原始数据进行标准化处理后的数据见表1，其中Y代表编制总量.

表1 标准化处理后的某县区编制核定相关指标数据

3.2 训练学习过程和预测结果

在MATLAB 7.0软件环境下，采用清华同方超强TP120 1800(Pentium D3.2GHz)主处理器并拥有2GB内存的PC机进行实验.

⑴ 训练确定SPREAD.参数SPREAD代表RBF网络的扩展速度，其默认值为1.SPREAD越大，函数拟合越平滑，但是逼近误差会变大，需要的隐藏神经元也越多，计算也越大.SPREAD越小，函数的逼近会越精确，但是逼近过程会不平滑，网络的性能差，会出现过适应现象.

实验中，SPREAD的初始值取为1，取SPREAD值在1～4范围训练测试，观察不同的SPREAD值对最终输出的影响.通过训练观察拟合误差可知，两类数据均表现出：当SPREAD取值从1逐步增加到2时，网络输出值接近于真实值，但是当SPREAD取值增加到3时，训练样本的输出值误差增大，进一步SPREAD取值增加到4时，误差进一步扩大.经过对两类数据反复试验测试，最终确定SPREAD=2，此时拟合最佳，网络的输出最接近于实际值.

⑵ 利用GCV准则优化确定中心宽度σ值首先采用试错法在1～4范围内选择合适的中心宽度σ值，观察拟合结果，然后通过GCV准则对其进行优化.具体做法如下：分别取目标误差E1=0.02，E2=0.008，E3=0.002，E4=0.0002，E5=0，设置SPREAD=2，观察网络拟合结果.采用正交最小二乘学习算法,分别对两类共16组数据进行训练学习和拟合分析.当网络学习达到各预定训练目标时，两类数据网络参数见表2、表3.

可以看出：当训练目标值越小时，若目标拟合精度越高，函数的中心宽度σ值就越小，同时隐层的神经元数量就越多.若设定目标E5=0，此时RBF网络的中心个数为8，和样本个数相同，为过拟合.

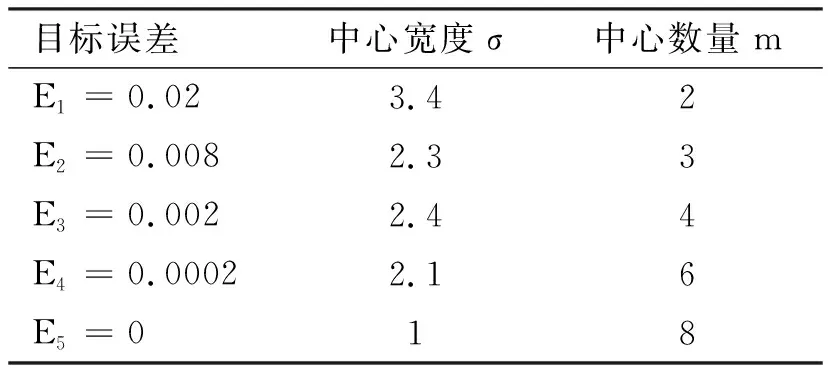
表2 第一类数据的各学习目标网络参数

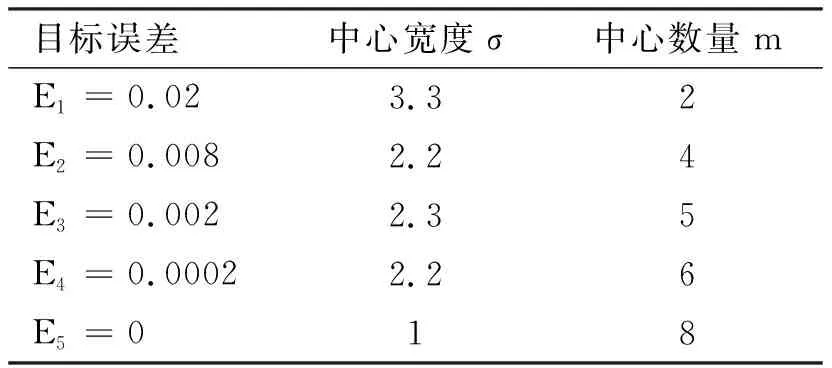
表3 第二类数据的各学习目标网络参数

下面利用GCV准则分别对两类数据各基函数的中心宽度σ进一步优化.

利用式(2)计算各不同的宽度值σ取对应GCV的值，通过实验计算和σ-GCV值曲线图可以看出，对第一类数据：当σ=1.33时GCV有极小值，因此可以把第一类数据的σ取值优化在1.33；对第二类数据：当σ=1.42时GCV有极小值，因此，可以把第二类数据的σ取值优化在1.42.σ-GCV值曲线如图1、图2所示.

图1、图2中，横轴表示σ取值，纵轴表示计算出的对应的GCV值.后文将利用训练好的网络进行预测，并结合传统未引入GCV准则的RBF网络预测结果进行对比.

⑶ 训练确定误差值

下面通过训练学习确定目标误差值.分4组且每组各取4个样本实验，样本目标误差值分别取E1=0.02，E2=0.008，E3=0.002，E4=0.0002训练，第一组样本网络的拟合情况见图3所示.

图3中，横轴表示目标误差，纵轴表示拟合误差，Wi表示第i个样本的拟合误差值.从实验结果可以看出第一类数据当E2=0.008时相对拟合最佳，此时中心宽度为2.3，中心数量为3；第二类数据当E3=0.002时拟合最佳，此时中心宽度σ均取2.4，中心数量为4.至此，网络训练学习完毕.

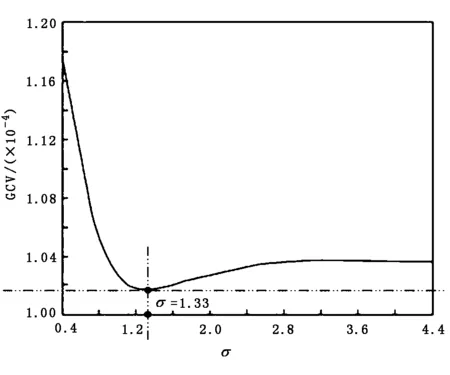
图1 第一类数据的σ-GCV值

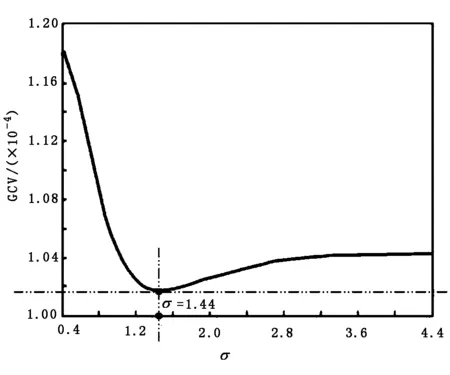
图2 第二类数据的σ-GCV值

图3 误差拟合变化趋势

为了对比验证网络预测的准确性，取1998—2011年共14组样本数据作为网络的输入，1998—2004年数据作为一类，2005—2011年数据作为一类，使用训练好的网络对2012、2013、2014年编制总量预测，对2个子网络的输出按式(5)做加权，对子网络整合，得到2012、2013、2014年编制总量预测值.使用传统的正交最小二乘法算法，不引入GCV准则以及不对样本进行分类建立子网络，建立编制总量预测的RBF网络模型预测.两种预测方法的结果列于表4中.

可见，没有引入GCV准则及分类建立的RBF网络的预测值精确度不如改进的RBF网络预测值的精确度高.

拟合值和实际值对比结果如图4所示.图4中TRUE代表实际值，Y1代表改进RBF算法预测值，Y2代表传统RBF算法预测值，Y3代表线性回归模型预测值.

表4 两种预测方法结果对比

从图4可以看出，三条曲线中，曲线Y1与曲线TRUE的拟合度是最佳的，表明了基于改进的RBF网络算法建立的网络模型对编制总量的预测精度更高，比使用传统RBF算法网络模型和线性回归模型进行编制总量预测效果更好.

图4 拟合值和实际值对比

4 结论

在当今政府管理工作的新形势下，基于改进的RBF网络算法，对某县区政府编制总量进行了预测.预测结果表明，基于改进的RBF网络算法比基于传统RBF网络算法的预测值误差更小，精度更高，因此能更好地满足编制管理部门实际工作的需要.虽然本文对RBF神经网络算法进行了部分改进，但仍需要进一步深入研究，以提高网络的时效性和预测结果的准确率；同时，今后应研究利用主流高级编程语言开发客户端程序，提高研究的实际应用价值.