随机风对某型火箭布雷弹落点散布的影响

阚菲菲，白晨曦，张学锋

(安徽工业大学计算机科学与技术学院，安徽马鞍山243032)



随机风对某型火箭布雷弹落点散布的影响

阚菲菲，白晨曦，张学锋

(安徽工业大学计算机科学与技术学院，安徽马鞍山243032)

摘要：随机风是影响火箭布雷弹落点散布的重要因素之一。为了研究随机风对火箭布雷弹落点散布的影响，建立了随机风模型和火箭布雷弹弹道模型，搭建了仿真实验场景，对随机风影响下的火箭布雷弹弹道和弹丸落点进行了模拟。通过仿真，分析随机风对火箭布雷弹落点散布的影响规律，为提高火箭布雷弹射击精度、减小落点散布、修正弹道提供实验依据。

关键词：随机风；火箭布雷弹；落点散布；密集度；弹道仿真

0引言

射击精度是衡量武器性能的一项重要战术指标[1]，包括射击准确度和射击密集度，前者是指火箭布雷弹平均落点相对于瞄准位置的偏差程度，描述了落点的系统性偏差；后者是指火箭布雷弹落点相对于平均落点的密集程度，描述了落点散布的随机特性。

影响射击精度的主要原因[2-3]，除武器之外，主要是由弹丸实际弹道与理想弹道之间的差异造成，包括：系统误差，如气温、气压、弹丸质量等与标准值间的差距，这些可以通过相应理论计算进行修正；随机误差，如弹丸出炮口时的扰动、射击时火炮的跳动和随机风等，由于它们具有不可知性，因此修正起来具有一定的难度。

火箭布雷系统是一种新的反坦克武器系统，是现代反机动作战的有效武器。它是利用火箭发动机作动力，将装填地雷的战斗部发射到预定距离上空，通过分离机构将地雷撒布到地面,构成一定面积的地雷场。

火箭布雷弹的发射试验，分为开舱实验和不开舱实验。开舱实验是为了检查地雷的散布情况，不开舱实验是为了检查火箭布雷弹落点的密集度。本文主要研究在不开舱的情况下，随机风对弹丸射击密集度的影响，通过建立布雷弹飞行的动力学模型及随机风的模型，并将二者统一起来，进行弹道仿真，分析实验数据，总结出随机风对弹丸射击密集度的影响关系。

1落点散布

所谓落点散布，是指在相同的发射条件下，用大量的火箭布雷弹对同一目标区域进行多次发射实验时，这些火箭布雷弹的落点会各自分散在目标周围。在相同的原始发射条件下，火箭布雷弹的落点相对于平均落点的坐标满足正态分布，设某个落点的坐标为(x，z)，则有

(1)

式中：ρ为常量，通常取值为0.477；Ex为火箭布雷弹的纵向射程(或距离)偏差；Ez为火箭布雷弹的横向方向偏差。

对于不同类型的火箭弹，衡量密集度的方法也不一样。本文所研究的火箭布雷弹，根据《火箭炮定型试验规程》(GJB 349.13A—1997)中的规定，采用立靶密集度进行衡量。

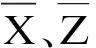
(2)

纵向射程偏差Ex为

(3)

横向方向偏差Ez为

(4)

Ex，Ez值越小，其射击密集度越高，火箭布雷弹的落点散布越集中，射击实验效果越好[4-6]。

2弹道数学模型的建立

火箭布雷弹作为一个力学对象，其在空中的运动属于刚体的一般运动，可分为质心运动和围绕质心的运动2种。对于火箭布雷弹来说，围绕质心的运动对质心运动的影响是次要的，也就是说，布雷弹的旋转运动，对其前进运动不会产生较大的影响。因此，在本文的研究中，将火箭布雷弹当作质点来进行研究。在研究火箭布雷弹的运动规律时，需要一定的参考系作为基准，本文主要用到以下2种参考坐标系。

1)地面坐标系(ground axes)：用O-xyz表示，是指与地面固连的坐标系。原点O位于火箭布雷弹发射点，Ox轴在发射面与弹道起点水平面的交线，顺着射向为正方向，Oy轴垂直于地面，取向上为正，Oz轴垂直于Oxy平面，方向依右手法则确定。

2)弹体坐标系(body axes)：用O-xbybzb表示。原点O在火箭布雷弹质心，Oxb轴与火箭布雷弹的几何纵轴一致，指向弹头方向为正，其余两轴位于弹体赤道平面内，Oyb轴在弹体纵向对称平面内与Oxb轴垂直，方向取向上为正，Ozb轴与Oxbyb平面垂直，方向依右手法则而定。

在本文中的研究中，先进行如下假设：①攻角为零；②将火箭布雷弹视为刚体；③忽略柯里奥利加速度的影响；④假设重力加速度的大小和方向均保持不变；⑤假设火箭布雷弹在瞬时的质量不变，即采用固化原理；⑥弹体外形和质量分布是均匀的、轴对称的，质心在火箭布雷弹几何纵轴上；⑦实际地球表面为曲面，但当射程≤80 km时，可视为平面处理[7]。依据上述参考坐标系之间的关系及假设条件，仅考虑运动时影响火箭布雷弹的主要因素，建立火箭布雷弹运动方程如下：

(5)

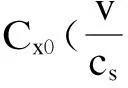
3随机风数学模型的建立

大气中空气的运动与气温、气压、空气运动所经地表面的性质和地球旋转等因素有关，这种复杂的关系导致了风在时间和空间上的很大变化[9]，因此对风的求解较困难。实际研究中，常采用简化风场模型。以射击面为基准，可将水平风分解为横风和纵风，如图1所示。

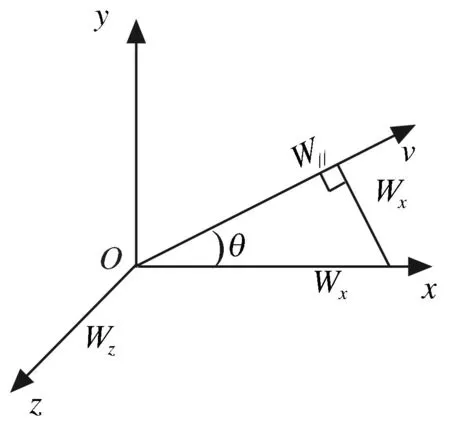
图1　风速分解图

横风Wz是垂直于射击面的风，与Oz轴方向一致时取正；纵风Wx是平行于射击面的风，与Ox轴方向一致时取正。纵风Wx又可进一步分解为平行风W∥和垂直风Wx⊥，其中，平行风W∥平行于布雷弹速度V，垂直风Wx⊥则垂直于速度V，则有：

(6)

对于火箭布雷弹的运动而言，Wz和Wx⊥对其影响本质是一样的，都称为垂直风，实际研究中，只需研究其中1种即可。

风主要是通过影响速度三角形的相互关系来影响火箭布雷弹的飞行。其中，地速V为布雷弹质心相对于大地的速度，决定了惯性力的大小和方向，空速U为布雷弹质心相对于大气的速度，影响作用于布雷弹上的空气动力的大小，风速W为空气的移动速度，影响速度三角形的相互关系[10]，如图2所示。

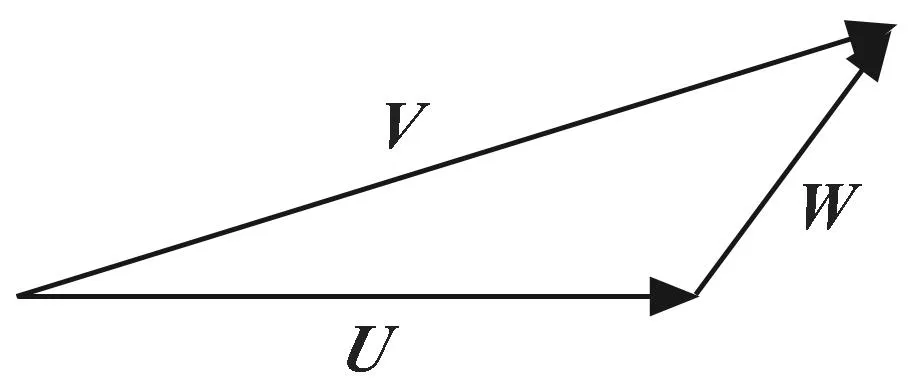
图2　速度三角形

通常情况下，研究风对火箭布雷弹飞行的影响时，先将风速矢量W沿地面坐标系各轴分解为W=[WxWyWz]T，当各分量与其对应坐标轴方向一致时为正，反之为负。当有风存在时，通过空速U和对应的攻角α及侧滑角β(即火箭布雷弹的纵向对称平面与速度矢量V之间的夹角)，来计算作用在布雷弹上的空气动力和动力矩。由此，在风干扰下，火箭布雷弹的质心速度[11]为

式中，Vx，Vy，Vz分别为火箭布雷弹的质心速度沿弹体坐标系的3个分量。

随机风是指风速和风向均随时间和位置而随机变化的风。为了描述随机风的模型，先进行如下假设：①假设风速是平稳的随机过程，其统计特性(均值和方差)不随时间和位置变化；②假设风向是随机的，其方向角符合均匀分布；③假设风速大小服从正态分布。

将风速矢量W在地面坐标系上进行分解，分量为Wx、Wy、Wz，并设定两方向角α1和α2，两者均服从均匀分布，其中α1为风速W与Ox轴的夹角，α2为风速W在yOz平面的投影与Oy轴的夹角，如图3所示。

图3　风向量在坐标系中的分解示意图

由图3可知：

(7)

对于风速，则服从正态分布，其密度函数为

(8)

式中:ω为风速;μ为随机风的均值;σ为随机风的标准偏差[12]。

4仿真模拟

4.1仿真场景的建立

根据真实的军事实验基地，模拟仿真场景，并对火箭布雷车、火箭布雷弹等进行3D建模，导入仿真的实验基地。

在场景中，可自由设置火箭布雷弹发射的初始参数，包括火箭布雷车坐标、射角、初速、火箭布雷弹直径、火箭布雷弹质量和基础风向等。图4为火箭布雷仿真演练系统的实验场景。

图4　火箭布雷仿真演练系统的场景

4.2仿真过程的实现

求解火箭布雷弹的运动方程时，需给出相关原始参数。在标准条件下，各参数取值为：火箭布雷弹质量m=57.91 kg,弹体直径d=0.122 m,初始速度v=44.5 m/s,重力加速度g=9.8 m/s,空气密度ρ随高度变化。

根据火箭布雷弹飞行力学模型，联立所建随机风模型，采用经典的四阶龙格库塔法，进行弹道计算，并通过仿真实验平台，实现火箭布雷弹整体飞行过程的模拟。火箭布雷弹飞行瞬间的姿态模拟如图5所示。

图5　火箭布雷弹飞行瞬间的姿态模拟

4.3随机风的仿真

根据参考文献[10]中不同高度的风的均值μ和标准差σ的值，模拟北纬20°～40°七月的随机风场。其中，随机风的风速大小通过随机函数生成，风向则以基础风向和随机的扰动来决定。表1所示为随机风随着高度变化时，均值和标准差的取值。

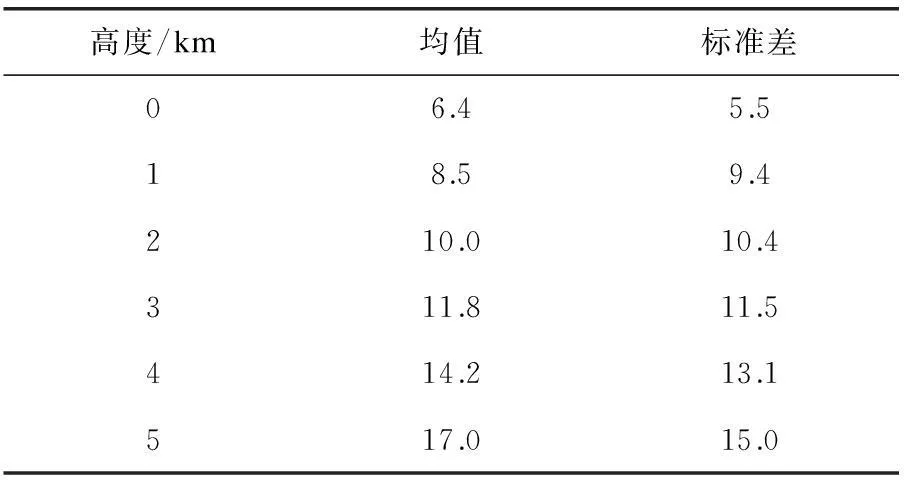
表1　随机风随高度变化的关系　m·s-1

据此模拟的某发火箭布雷弹发射过程中的随机风曲线如图6所示。

图6　随机风场的模拟

因高度不同，随机风的风速均值也不同，且通常是高度越高，风速越大。从仿真结果可以看出，在火箭布雷弹刚刚发射和落地阶段，风速较小，飞行到最高处时(时间轴的中间段)，风速最大，符合实际情况。

5结果分析

5.145°射角时横风对落点散布的影响

横风Wz垂直于射击面，会造成火箭布雷弹在横向方向的偏移。设置初始射角为45°，进行20次弹道仿真，其弹丸落点散布情况如图7所示。

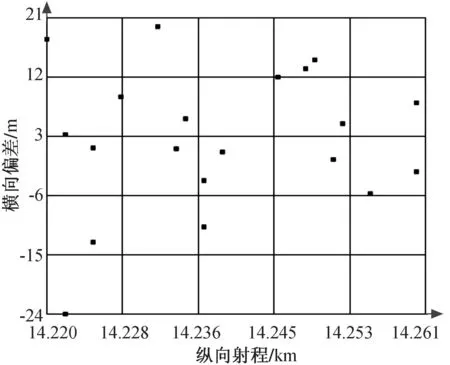
图7　横风作用下的落点散布情况

5.2纵风作用下的落点散布情况

纵风Wx是平行于射击面的风，根据前面的分析，此处只研究水平风W//对火箭布雷弹落点散布的影响。采用上述方法，同样进行20次弹道仿真实验，其弹丸落点散布情况如图8所示。

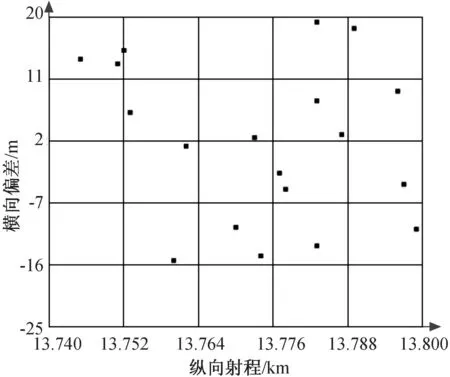
图8　逆风作用下的落点散布情况

5.3横风时不同射角下的落点散布情况

通常情况下，火箭布雷弹发射的最小射角为25°，最大射角为48°，且当射角为45°时，射击实验取得最大的射程。根据上述分析45°射角下横风(纵风)对火箭布雷弹落点散布影响的方法，研究不同射角(25°～48°，以5°为间隔)时，横风对火箭布雷弹落点散布的影响情况。

由于原始数据量较大，此处不再给出原始数据，直接给出统计分析后的计算结果，如表2所示。

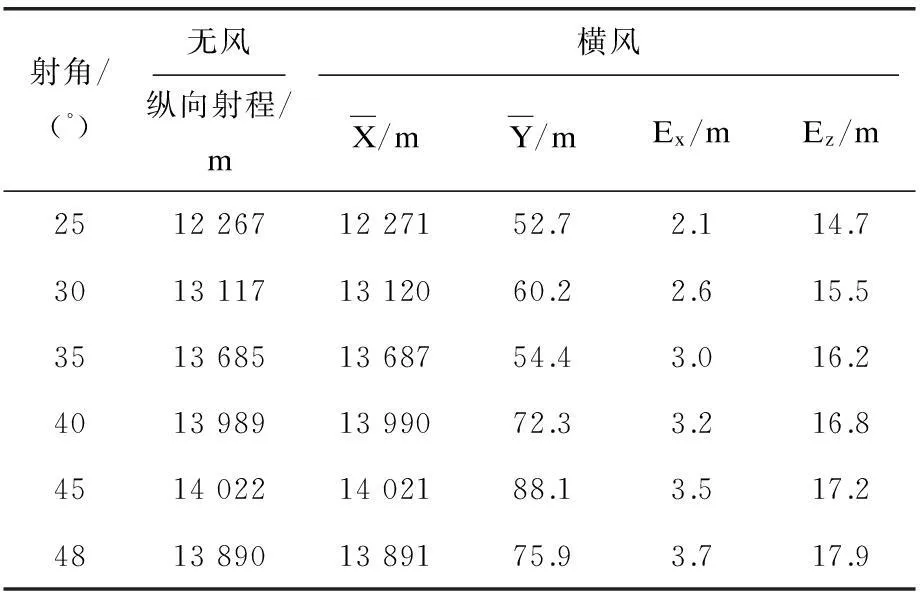
表2　横风时不同射角下弹丸落点散布情况

5.4纵风时不同射角下的落点散布情况

根据上述研究横风对不同射角的火箭布雷弹落点散布影响的方法，观察不同射角时，纵风对火箭布雷弹落点散布的规律，原始数据此处不再赘述，数据统计分析后的结果如表3所示。

表3　纵风时不同射角下弹丸落点散布情况

由表3结果分析可知，无风条件下，射角为45°时，火箭布雷弹的发射达到最大纵向射程为14 022 m，符合实际情况。此外，横风对横向方向偏差的影响大于对纵向射程的影响，纵风对纵向射程的影响大于对横向偏差的影响，随着射角的增大，对弹丸落点散布的影响也随之增大，弹丸落点散布的密集度也越高，符合实际情况。

6结语

通过对随机风和随机风扰动下的弹丸落点散布的仿真，表明随机风是影响火箭布雷弹飞行的重要因素之一。在布雷系统设计过程中，应充分考虑随机风的影响，以保证系统有足够的稳定性和可靠性。

[参考文献]

[1]曹宁,王晓锋，徐亚栋，等.车载炮射击密集度逐步回归分析[J].弹道学报，2012,24(4)：42-46.

[2]孙艳馥，袁志华，王欣.随机风扰动下的弹丸落点散布仿真分析[J].弹箭与制导学报，2009,29(1)：209-211.

[3]魏惠之，朱鹤松，汪东晖.弹丸设计理论[M].北京：国防工业出版社，1985.

[4]张敏.扰动因素对单兵火箭弹散布的影响研究[D].长沙：国防科学技术大学，2012.

[5]浦发.外弹道学[M].北京：国防工业出版社，1980.

[6]GADE S V，ROJATKAR P T.Effect of vehicle dynamicson the performance of a multiple rocket launcher system: An experimental assessment[C]//Proceedings of 17th International Symposium on Ballistics.Gauteng Province:Midrand，1998:67-74.

[7]徐明友.火箭外弹道学[M].北京：兵器工业出版社,2004.

[8]马艳琴，马大为，乐贵高.某型号火箭布雷弹弹道研究[J].弹箭与制导学报，2003,24(1)：157-159.

[9]国防科学技术工业委员会.大气风场(0～25公里):GJB 366.2—87[S].北京：国防科工委军标出版发行社，1987.

[10]李卫丽，严洪森，张维琴.风干扰下某型导弹的弹道仿真[J].计算机技术与发展，2011，21(1)：246-249.

[11]金华，孟云鹤，戴金海.风扰动下的卷弧翼弹六自由度弹道模型及仿真[J].系统仿真学报，2007,19(16)：3627-3630.

[12]陈云霞，康锐，孙宇锋.风对火箭布雷弹飞控系统可靠性影响的仿真研究[J].系统仿真学报，2005，17(2)：275-278.

责任编辑：陈亮

doi:10.3969/j.issn.1671-0436.2016.03.007

收稿日期：2016- 03-17

基金项目：安徽省教育厅高校自然科学研究重点项目(KJ2016A085)

作者简介：阚菲菲(1992—)，女，硕士研究生。

中图分类号：TP391.9

文献标志码：A

文章编号：1671- 0436(2016)03- 0027- 06

Shell Distribution of a Mine-laying Bomb Under the Influence of Stochastic Wind

KAN Feifei，BAI Chenxi，ZHANG Xuefeng

(School of Computer Science and Technology,Anhui University of Technology,Maanshan 243032)

Abstract：Stochastic wind is one of the important factors affecting the shell distribution of the mine-laying bomb.In order to study the influence of stochastic wind on the mine-laying bomb,a stochastic wind model and a mine-laying bomb trajectory model were established,a simulation experiment scenario was set up to simulate the mine-laying bomb trajectory and ballistic placement under the influence of stochastic wind.Through the simulation,the influence of stochastic wind on the mine-laying bomb shell distribution was analyzed,which provided an experimental basis for improving fire accuracy,decreasing shell distribution and correcting trajectory.

Key words：stochastic wind；mine-laying bomb；shell distribution；density；trajectory simulation