基于数值分析不同填料下扶壁式挡墙土压力研究

吴帅

(重庆交通大学土木工程学院，重庆400074)



基于数值分析不同填料下扶壁式挡墙土压力研究

吴帅

(重庆交通大学土木工程学院，重庆400074)

摘要：不同填土情况下，运用Flac3D数值软件模拟了扶壁式挡墙侧向土压力分布情况，重点分析了砂土、黏土、多年冻土作为填料对侧向土压力分布的影响。结果表明：当砂土φ>30°，作用于墙背上的侧向土压力将达到稳定；黏性填土φ值在15°～25°变化时，侧向土压力先变小后变大，并趋于稳定，当c>20 kPa时，墙背侧向土压力趋于稳定；多年冻土由于黏聚力大，改变φ、c，侧向土压力没有明显变化。另外，侧向土压力沿墙高缓慢增加，在底部出现回弯，与规范理论计算呈线性变化不一致，这主要是由于挡墙墙背、扶壁与填土的摩擦减压作用使计算结果小于理论值，作用于墙背上的侧向土压力比理论计算主动土压力小40%左右。

关键词：Flac3D；数值模拟；侧向土压力；扶壁，砂土；黏土

0引言

土压力是填土与支挡结构相互作用的结果，计算土体作用于结构上的作用力。这是一个古老的课题，时至今日，对土压力的研究依然在继续，其大小不仅仅与挡土墙的高度、填土的性质、挡土墙的刚度和位移有关[1]。土压力理论的研究可以归纳为2种：一是基于极限平衡理论；二是基于半数值半解析方法。传统理论(如库伦、朗肯理论)是在极限状态下计算土压力，而实际上挡墙并没有达到极限状态，因此真实的土压力与传统理论计算所得的土压力存在差异。有限元法是半数值半解析的一个分支，从Clough和Woodward首先采用有限元法分析土坝问题以来，有限元法在岩土工程中的应用发展迅速，并取得了巨大突破。董正筑、黄平[2]分析了P Gussmann提出的滑移单元法，并采用有限元离散化，利用最优化过程求得刚性挡土墙侧土压力的最佳上限解。陈页开[3]通过模型试验和数值分析得出，作用在挡墙上的土压力分布与墙体变位模式有关。章瑞文[4]通过对挡墙主动土压力逐层渐进法的研究，对墙面摩擦角、滑裂面摩擦角随墙高变化的问题提出了解决方法，研究结果表明挡墙土压力分布呈非线性，且变滑裂面为一曲面。为了研究不同填料变形协调情况下，土压力随挡墙深度的分布规律，本文运用Flac3D数值分析软件模拟了扶壁式支挡结构在不同填料下的土压力分布情况，并分析出现这种结果的原因，以寻求不同填料作用下的土压力分布规律。

1Flac3D数值模拟分析

1.1计算模型

由于扶壁式挡土墙的纵横比在一般情况下很大，可认为纵向的变形为0，因此可简化为平面应变问题。在建立分析模型时，墙后填土与挡墙地基定义为实体单元，采用刚性基础，模型纵向长度5.2 m，挡墙结构如图1，数值分析模型见图2。

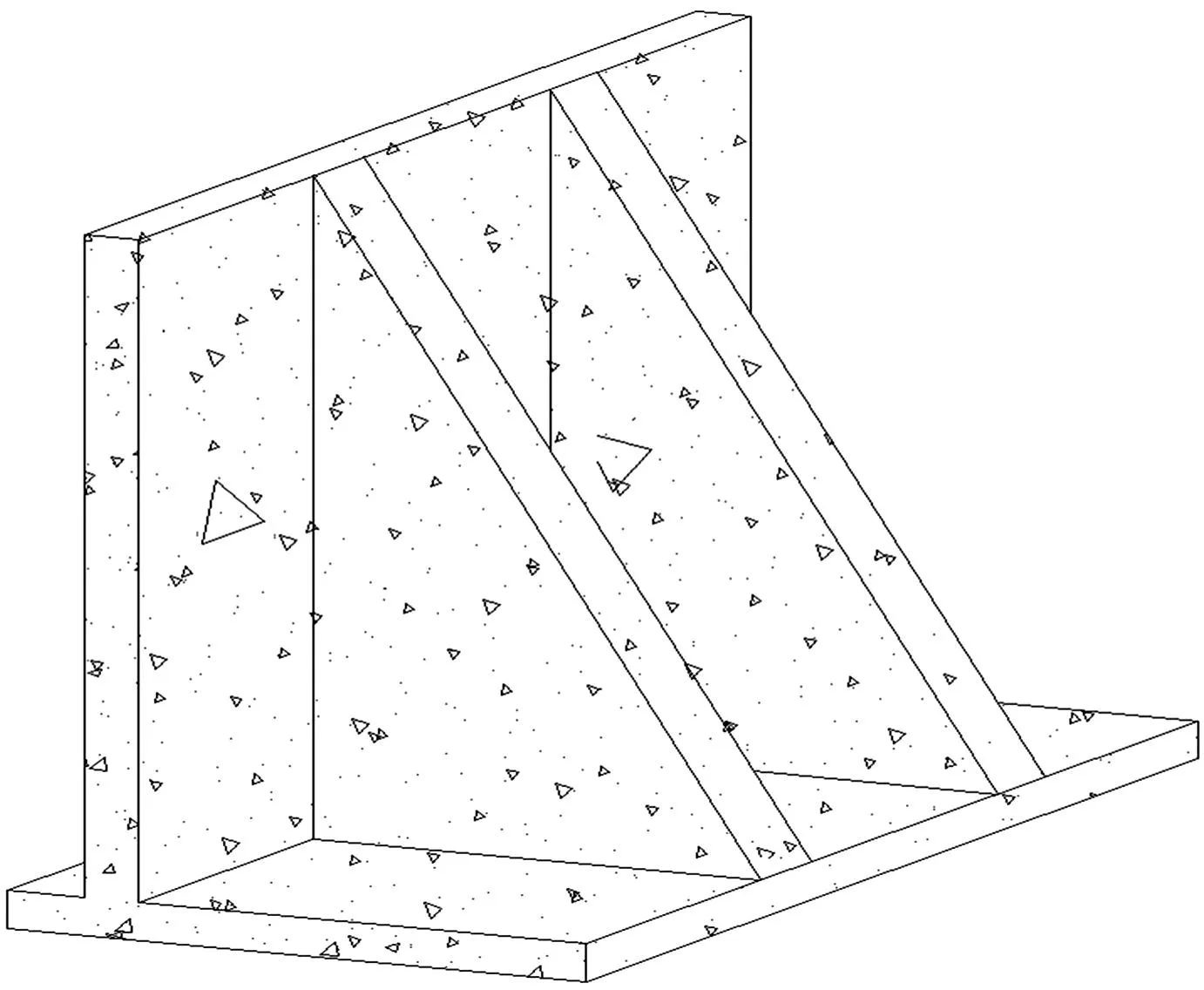
图1　挡墙结构

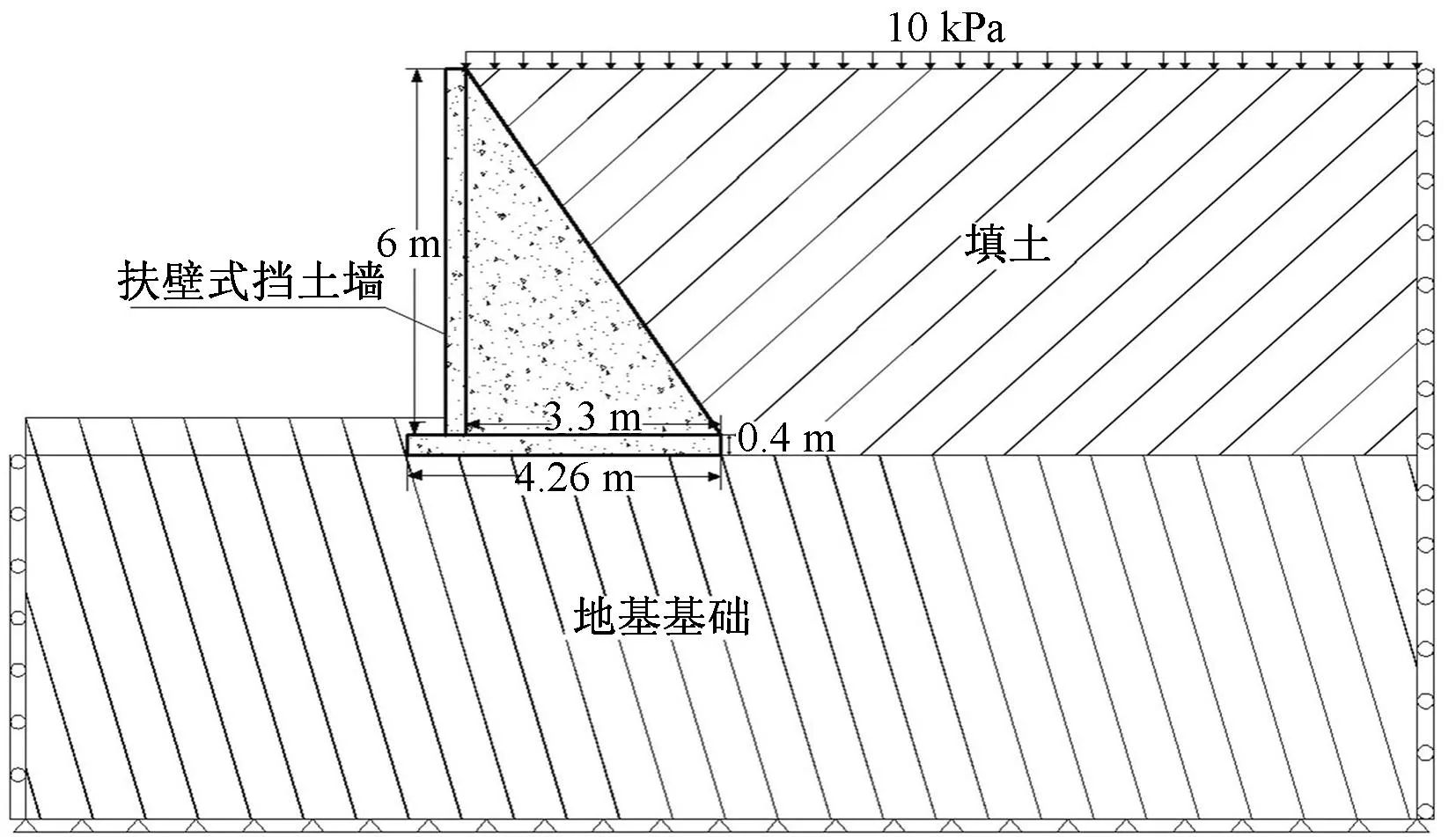
图2　数值分析模型

1.2本构模型

由于土和钢筋混凝土的变形模量存在较大差异，为了提高分析的可靠性，使其与实际情况相吻合，需要在挡土墙结构和土的界面上设置接触面。Mohr-Coulomb屈服准则较为符合岩土和混凝土材料的屈服和破坏特征，故采用Mohr-Coulomb屈服准则，本文采用弹塑性模型。在塑性屈服以前服从弹性应力-应变关系，塑性屈服以后，应力增量与应变增量服从弹塑性本构关系[5-6]。

1.3边界条件

如图2所示，长度方向为X向，纵向为Y向，高度方向为Z向，在模型的最左边和最右边施加X向的约束，纵向两端端面施加Y向约束，模型底面施加X、Y、Z三方向约束。

1.4荷载类型

在挡土墙有限元分析范围内，除了考虑重力荷载的作用外(墙面风荷载可以不考虑，对计算结果影响不大)，竖直方向上有大小为10 kPa的力作用于填土，如图2所示。

1.5材料参数

不同地区的填土性质不同，为了尽可能与实际工程情况相吻合，参考国内外已经完成的工程，本文中的墙后填料分为3类，即砂土、黏土和多年冻土，挡墙地基设为刚性。详细材料参数如表1。

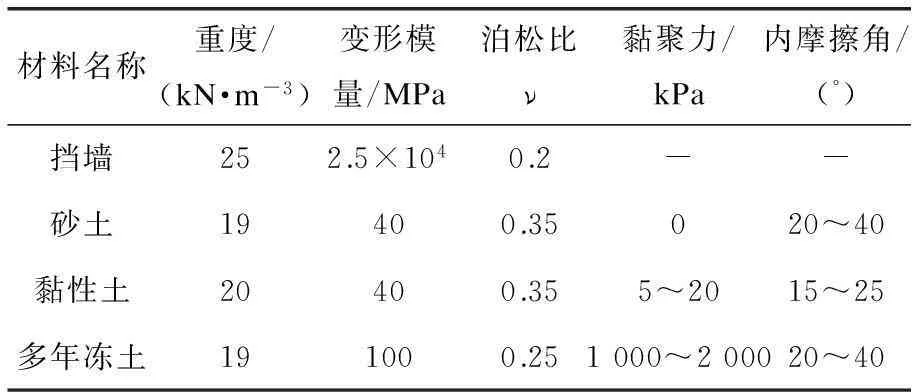
表1　材料物理力学参数

2计算结果分析

土压力与墙后填料、挡墙本身和地基密切相关。本文采用有限元法，通过Flac3D数值分析软件，模拟分析了不同性质的填土作用下墙背的受力情况[7-11]。

2.1墙背侧向土压力

改变填料的参数，在挡墙高度方向上，选取若干点监测侧向土压力的变化，将监测结果绘成曲线图。监测结果分为2类，一类是墙背侧向土压力，一类是垂直于扶壁的土压力，扶壁沿深度监测(深度3 m处开始)。侧向土压力分布情况如图3～6。

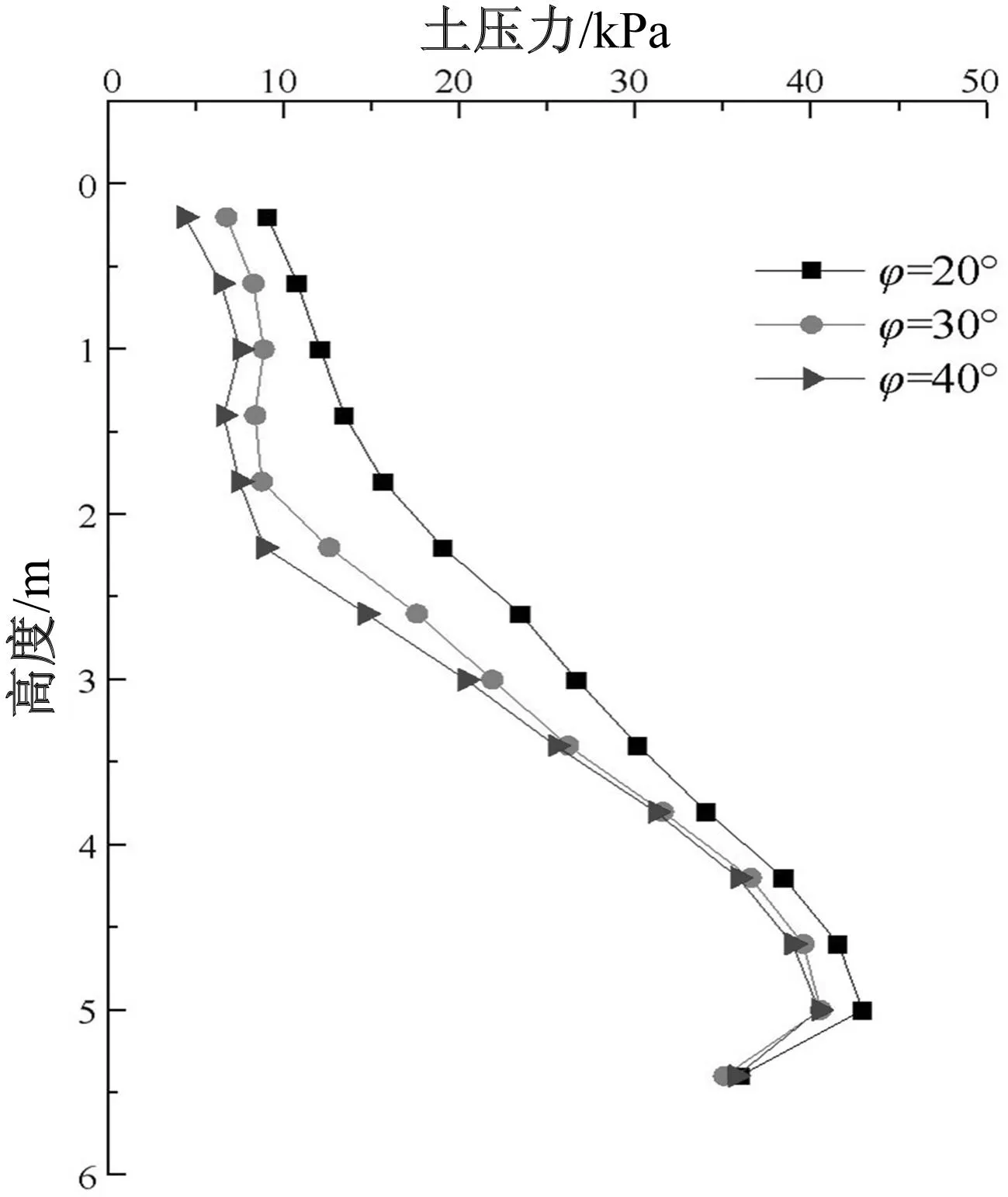
图3　砂土墙背侧向土压力

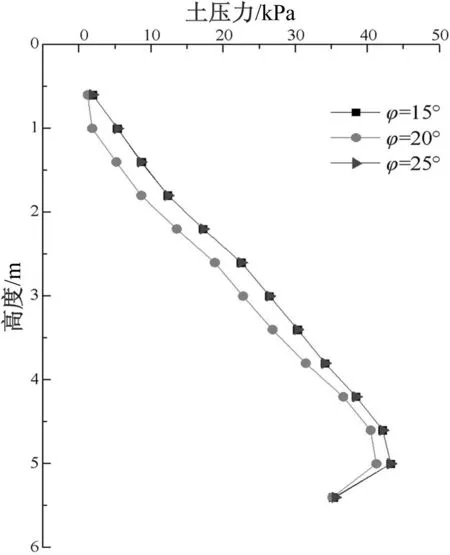
图4　黏性土c=5 kPa时墙背侧向土压力

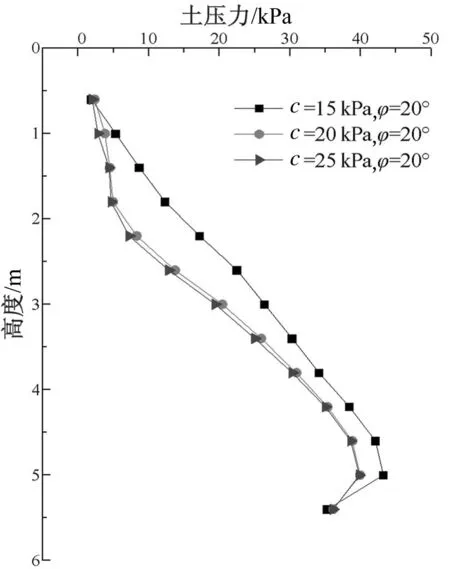
图5　黏性土φ值相同时墙背侧向土压力

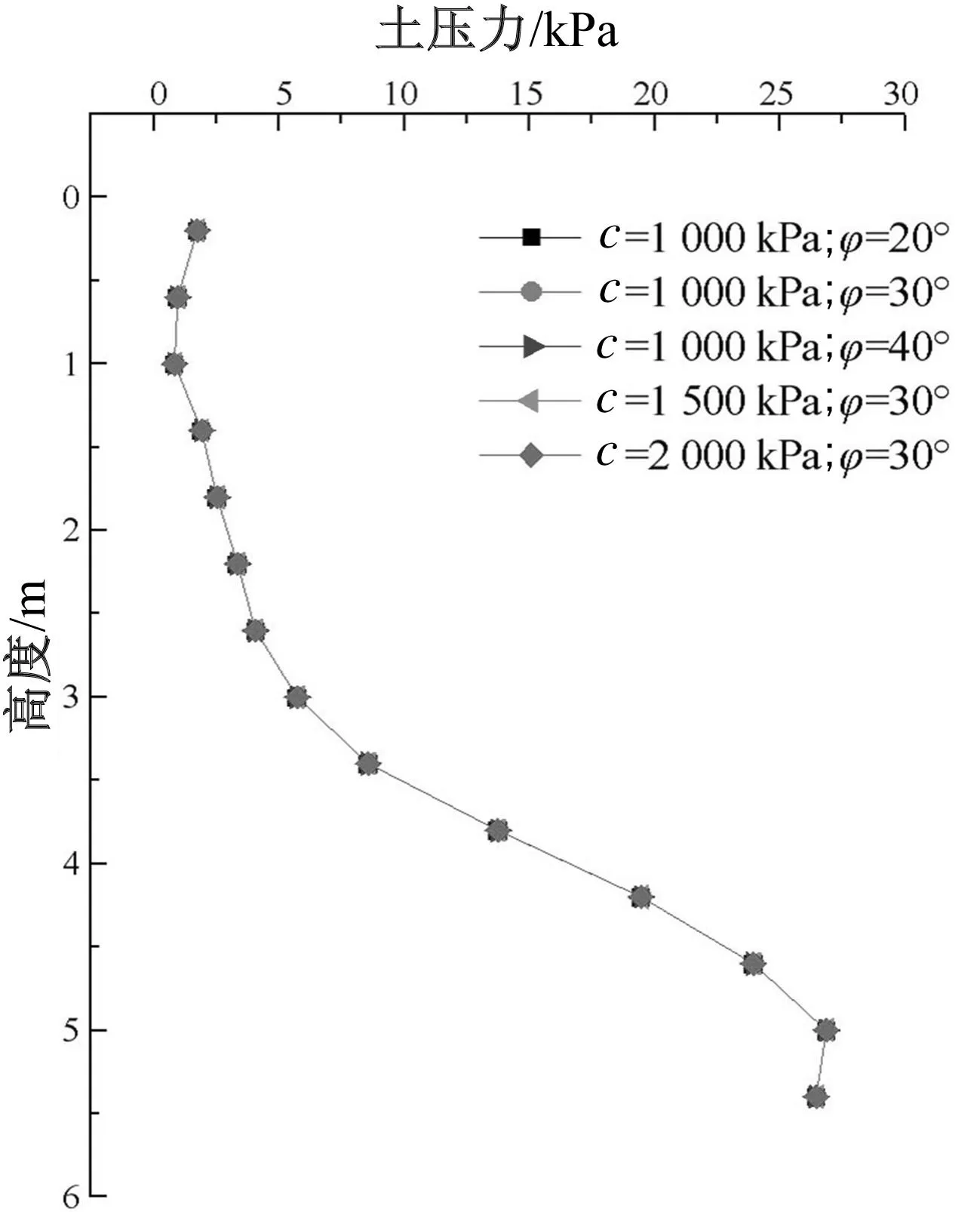
图6　多年冻土墙背侧向土压力

土压力数值计算结果分析：

1)当填土为砂土时，如图3所示，墙背侧向土压力呈非线性分布，底部侧向土压力增量逐渐变小，并出现回弯。当φ=20°时，墙背侧向土压力沿墙深度缓慢增加，侧向土压力呈近似直线分布，下部侧向土压力呈非线性分布，在靠近底部的位置出现了回弯现象；当φ=30°、φ=40°时，侧向土压力曲线呈非线性分布，在深度2 m位置处出现转折，墙底侧向土压力与φ=20°时类似。因此，当填料为砂土时，随着内摩擦角的增大，侧向土压力呈现逐渐减小的趋势，砂土φ>30°时，侧向土压力变化不明显，基本达到稳定状态。

2)当填土为黏性土时，如图4所示。当c=5 kPa，在φ值变化时，墙背侧向土压力呈非线性分布，沿墙深度方向逐渐增加，靠近墙底部侧向土压力逐渐减小并出现回弯。φ=15°、φ=25°时，墙背侧向土压力曲线重合，当黏土内摩擦角在15°～25°之间变化时，墙背侧向土压力先变小后变大，最后与φ=15°时重合，可认为当φ>25°时，墙背侧向土压力基本达到稳定。继续增加φ值，侧向土压力没有明显的变化。

3)当填土为黏性土时，φ值一定，改变c值的大小，如图5所示。当黏性填土c>15 kPa时，墙背侧向土压力逐渐趋于稳定，c=20 kPa时，墙背侧向土压力基本达到稳定状态。

4)当填料为多年冻土时，如图6所示，作用于墙背上的侧向土压力没有变化。当填土黏聚力增大到一定数值是时，改变φ值，继续增大黏聚力，对侧向土压力的大小没有影响。

以上4点与传统理论反映的土压力分布规律不一致，其原因可能是挡墙墙背与填土之间、扶壁与填土之间的摩擦作用(理论计算未考虑摩擦作用)抑制了土压力向下的传递，从而出现回弯现象。另外，经典计算中填土破坏面是一平面，但挡墙实际的破裂面为曲面，因此计算结果与传统理论存在差异。当填料为砂土时，墙背侧向土压力呈非线性分布，靠近底部的侧向土压力增量逐渐变小并出现回弯现象，当φ>30°时，侧向土压力趋于稳定；当填料为黏土时，侧向土压力沿墙深度方向非线性逐渐增大，靠近底部的侧向土压力减小，并出现回弯现象，当c>20 kPa时，墙背上的侧向土压力趋于相等；当填土是多年冻土时，由于黏聚力足够大，因此改变φ、c，作用于墙背上的侧向土压力不发生变化[12-16]。

2.2垂直扶壁土压力分析

不同填土对扶壁式挡墙中扶壁肋板的侧向压应力如图7～9所示。

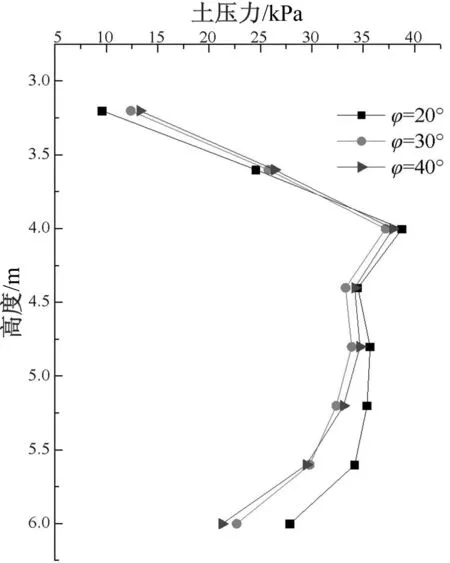
图7　砂土垂直扶壁土压力

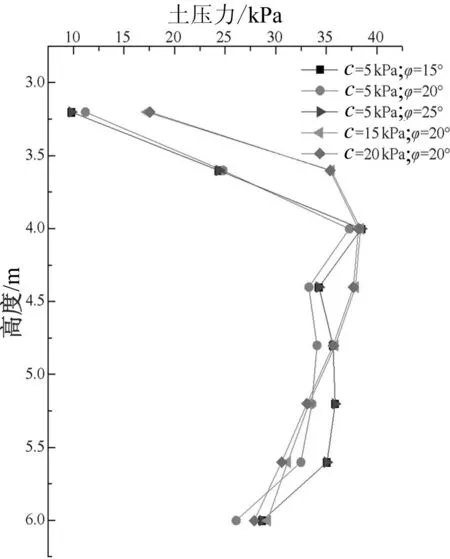
图8　黏土垂直扶壁土压力

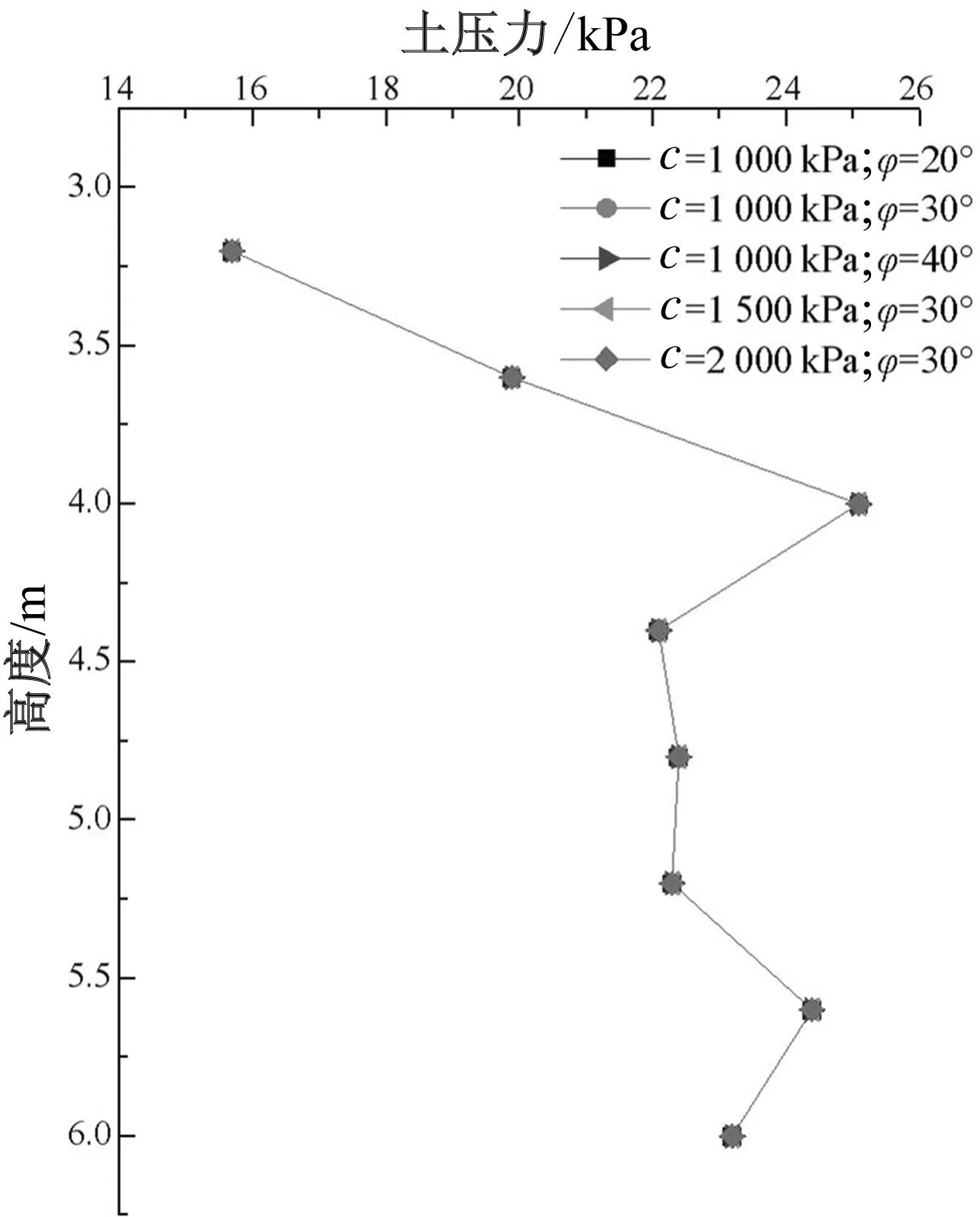
图9　多年冻土垂直扶壁土压力

从数值分析结果中提取了垂直于扶壁的土压力，图7、图8分别为砂土和黏土的土压力，图9为多年冻土的土压力，在3～5 m范围内，砂土与黏土变化规律相似，土压力缓慢增加，多年冻土垂直于扶壁的土压力在22 kPa左右。填料为砂土时，侧向土压力呈非线性变化，当φ>30°时，侧向土压力变化不大，基本稳定，墙背侧向土压力增加趋势缓慢，曲线基本重合。当黏土内摩擦角在15°～25°之间变化时，墙背侧向土压力先变小后变大，最后与φ=15°时重合，可认为当φ>25°时，墙背侧向土压力趋于稳定；黏土c>15 kPa时，墙背侧向土压力逐渐趋于稳定，c=20 kPa时，墙背侧向土压力曲线趋势相同，基本重合。填土为多年冻土时，改变φ、c的大小，作用于墙背上的侧向土压力不发生变化，垂直于扶壁的土压力与侧向土压力的规律类似。另外，由于垂直扶壁的土压力作用，设计时应考虑扶壁的抗剪、抗弯能力。

2.3经典理论与数值计算结果对比

本文对砂土、黏土理论侧向土压力和数值模拟计算所得的侧向土压力进行了对比，如图10。数值计算的侧向土压力明显小于理论计算的侧向土压力，分析原因为：扶壁挡墙中存在扶壁肋板，由于肋板及墙后填土和挡墙立板的摩擦作用产生减压效应，使数值计算的结果小于理论计算结果。从数值分析的结果可知，砂土侧向土压力相比理论计算结果减小40%，减压效果非常明显，因此在设计计算中，应该充分考虑填土与挡墙结构之间的摩擦减压效应。

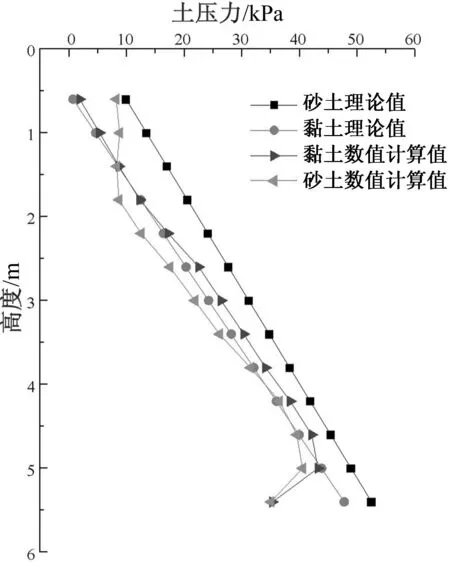
图10　经典理论与数值分析计算结果对比

3结论

1)在支挡结构中，砂土φ>30°时，墙背侧向土压力变化不明显，基本达到稳定状态；填料为黏性土时，φ值不变，改变c值的大小，当c>15 kPa，墙背侧向土压力基本达到稳定状态。

2)对于填土黏聚力达到一定数量级时，如多年冻土，改变填料的内摩擦角、黏聚力对挡墙受到的侧向土压力没有影响。

3)数值计算所得砂土、黏土的侧向土压力，比理论计算值减小40%左右。这主要是由填料与挡墙结构(扶壁肋板、立板)之间的摩擦减压效应引起的，在设计计算中要考虑其摩擦效应。另外，有垂直作用在扶壁上的力，设计中要充分考虑扶壁的抗弯、抗剪性能。

4)数值分析结果供参考使用，有待进一步在实际工程中验证[17]。

[参考文献]

[1]周应华，赵洪彬，郑玉辉.不同土性下L型挡土墙土压力研究[J].路基工程，2012(4):123-126.

[2]董正筑，黄平.土力学极限分析的滑移单元最优化计算法及侧土压力计算[J].岩土工程学报，1992，3(2):28-36.

[3]陈页开.挡土墙上土压力的试验研究与数值分析[D].杭州:浙江大学，2001.

[4]章瑞文.挡土墙主动土压力理论研究[D].杭州:浙江大学，2007.

[5]厉超，孟庆宇，解全一.互锚式挡土墙土压力分布规律研究[J].公路，2015(7):16-20.

[6]梁波，王家东，严松宏.垛式新型悬臂式挡墙的数值分析及应用探讨[J].岩土力学与工程学报，2006(增1):3174-3180.

[7]张华，陆阳.基于有限差分与离散元藕合的支挡结构数值计算方法[J].岩土工程学报，2009,31(9):1402-1407.

[8]胡斌,张悼元,黄润秋,等.FLAC3D前处理程序的开发及仿真效果检验[J].岩石力学与工程学报，2002(9)：1387-1391.

[9]刘继国，曾亚武.FLAC3D在深基坑开挖与支护数值模拟中的应用[J].岩土力学，2006,27(3)：505-508.

[10]郑文华.FLAC3D复杂模型interface建模方法探讨[J].土木建筑信息工程技术，2012(2)：67-70.

[11]刘春玲,祁生文,童立强,等.利用FLAC3D分析某边坡地震稳定性[J].岩石力学与工程学报，2004(16):2730-2733.

[12]刘莹骏，张运良.一种薄层接触单元的开发及FLAC3D实现[J].水利与建筑工程学报，2014，12(4)：1-8,49.

[13]CHANG Mingfang.Lateral earth pressure behind rotating walls[J].Canadian Geotechnical Journal,1997,34(2): 498-509.

[14]FANG Y S,ISHIBASHI I.Static earth pressure with various wall movements[J].Journal of Geotechnical Engineering,1986,112(3): 317-333.

[15]LI H,FOSCHI R O.An inverse reliability method and its application [J].Structural Safety,1998,20(3): 257-270.

[16]PAIK K H,SALGADO R.Estimation of active earth pressure against rigid retaining wails considering arching effect[J].Geotechnique,2003,53(7): 643-645.

[17]赵晓彦，胡厚田，唐茂颖.类土质高边坡开挖效应的离心模型试验及数值模拟研究[J].岩石力学与工程学报，2006(增2)：4047-4051.

责任编辑：唐海燕

doi:10.3969/j.issn.1671-0436.2016.03.004

收稿日期：2016- 03-30

作者简介：吴帅(1990—)，男，硕士研究生。

中图分类号：TU432

文献标志码：A

文章编号：1671- 0436(2016)03- 0013- 05

Earth Pressure of Counterfort Retaining Wall with Different Fillings Based on the Numerical Analysis

WU Shuai

(School of Civil Engineering,Chongqing Jiaotong University,Chongqing 400074)

Abstract：Lateral earth pressure distribution of counterfort retaining wall with different fillings was simulated on numerical software FLac3D with focus on the lateral earth pressure distribution with sand,clay and permafrost fillings.Results show that for sand,when φ>30 degrees,lateral earth pressure exerted on the retaining wall in the horizontal direction tends to be stable;for clay,when φ is between 15 and 25 degrees,lateral earth pressure first decreases,then increases,and keeps stable with c>20 kPa;for permafrost,due to its high cohesion,any change in φ and c causes no significant change in lateral earth pressure.In addition,lateral earth pressure slowly grows along the wall height with bending appearing at the bottom of the back,which is inconsistent with the linear change by the normative theoretical computing.This is mainly due to the pressure-decreasing friction between the retaining wall and fillings,which causes the calculation results less than the theoretical value:lateral earth pressure exerted on the counterfort retaining wall in the horizontal direction is about 40% less than the classical active earth pressure.

Key words：Flac3D;numerical simulation;lateral earth pressure;counterfort;sand;clay