基于B-S模型的上证50ETF期权定价研究*

张天凤，朱家明



基于B-S模型的上证50ETF期权定价研究*

张天凤1，朱家明2

（1.安徽财经大学金融学院，安徽蚌埠 233030；2.安徽财经大学统计与应用数学学院，安徽蚌埠 233030）

摘 要：针对已上市的上证50ETF期权定价问题，通过推导有红利的扩展Black-Scholes期权定价模型，并采用历史波动率法和GARCH模型两种方法计算期权价格的波动率，将波动率引入模型，使用MATLAB、EVIEWS软件，计算出不同波动率条件下上证50ETF期权的价格并与真实数据比较，发现GARCH模型能够使期权定价结果更准确。

关键词：上证50ETF期权；期权定价；GARCH模型；波动率

随着我国证券市场的发展，金融市场的交易越发活跃。投资者为稳定其收益，避免亏损，逐渐希望市场上出现更多的交易品种和合约组合设计来供他们规避风险。因此，投融资市场对金融衍生品的需求逐渐增大，上证50ETF期权在这种形势下被正式推出。期权作为一种金融衍生品，因其特殊性，在交易中往往承担着杠杆作用，它能让买方亏损有限盈利无限，卖方盈利有限而亏损无限。当然，期权作为商品的一种，也需要价格来确定它的价值，这就推动了对期权定价问题的研究。

1 文献回顾及问题的提出

1.1 文献回顾

由于我国仅推出了上证50ETF期权和比特币期权两类期权品种，我国在期权定价问题上的研究还没有很多可供参考的实时数据。其中，宋焕雨［1］（2015）利用B-S期权定价公式和数值方法对上证50ETF期权进行研究分析，发现B-S公式和二叉树模型能够很好地对上证50ETF期权价格定价，波动率模型的引入可以提高定价结果的准确度。陈守涛［2］（2015）推导出蒙特卡罗模拟随机模型，将其用于上证50ETF期权定价，认为利用蒙特卡罗模拟求解多标的资产期权是一个切实可行的数值方法。

1.2 问题的提出

在金融衍生品的定价中，期权定价无疑是最复杂的，然而它也是期权市场能否稳健有序运行的关键。早在1973年，Fischer Black和Myron Scholes［3］（1973）提出了著名的B-S期权定价公式。而由于公式应用条件的限制，在实际操作中运用得并不广泛。此外，还有Hull-white［4］（1987）随机波动率模型用对偶Monte Carlo模拟法比较了近似显示解的准确度，研究并分析了波动率参数的改变对期权价格的影响。而罗斯等人提出的与之相互映衬的二叉树法，即将时间段细分成更加微小的单位，所以其适用于更加复杂的期权定价［5］（2009）。为此，我们结合理论事实，采用扩展后的期权定价模型，考虑了红利支付情况，并将标的资产定为华夏上证50ETF，以期在实务运用中有更为广泛的应用。

2 沪深300股指期权定价的模型设定

2.1 经典的Black-Scholes模型

在欧式期权定价中，最经典的是B-S模型，利用模型的关键是假定所有投资者对期权定价都是风险中性的。经典B-S模型的基本假设条件有5个：投资者不能通过套利获得比其他投资者更高的利率，以无风险利率r作为标的资产的预期收益率，r是一个常数；标的华夏上证50ETF的价格变化遵循几何布朗运动；投资者在期权有效期内不能收到红利收益；证券市场没有卖空限制，投资者可进行做空交易；证券市场无摩擦，所有证券完全可分。

经典B-S模型：

欧式看涨期权定价公式：c=S0N（d1）-Ke-r（T-t）N（d2）

欧式看跌期权定价公式：p=Ke-r（T-t）N（-d2）-S0N（-d1）

式中S0为t=0时的标的ETF价格，K为合约到期执行价格，r为无风险利率，σ为标的ETF波动率，T-t为期权合约期限，N（x）为正态分布累积分布函数。

2.2 拓展的Black-Scholes模型

尽管经典的B-S定价公式较为简单，但在实际应用中并不广泛，这是因为基本假设条件的第三个经常不能得到满足，在期权合约期内通常会有一定的红利支付。由于欧式看涨期权和欧式看跌期权定价公式的指导原理相同，且欧式看跌期权的价格可以利用看涨期权与看跌期权的平价关系推出，故在此我们只以欧式看涨期权为例指导拓展的B -S模型。

假定标的资产价格S遵循几何布朗运动，则dS=μSdt+σSdz

由于期权价格G是标的资产价格S和时间t的函数G（S，t）

由伊藤引理得：

由于投资者都是风险中性的，因此期权价格是其期望收益值按无风险利率贴现的现值

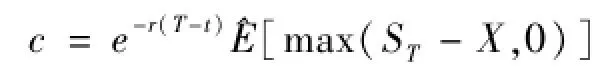
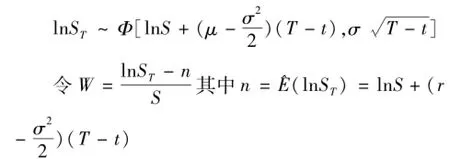
设f（ST），h（W）分别为 W的密度函数

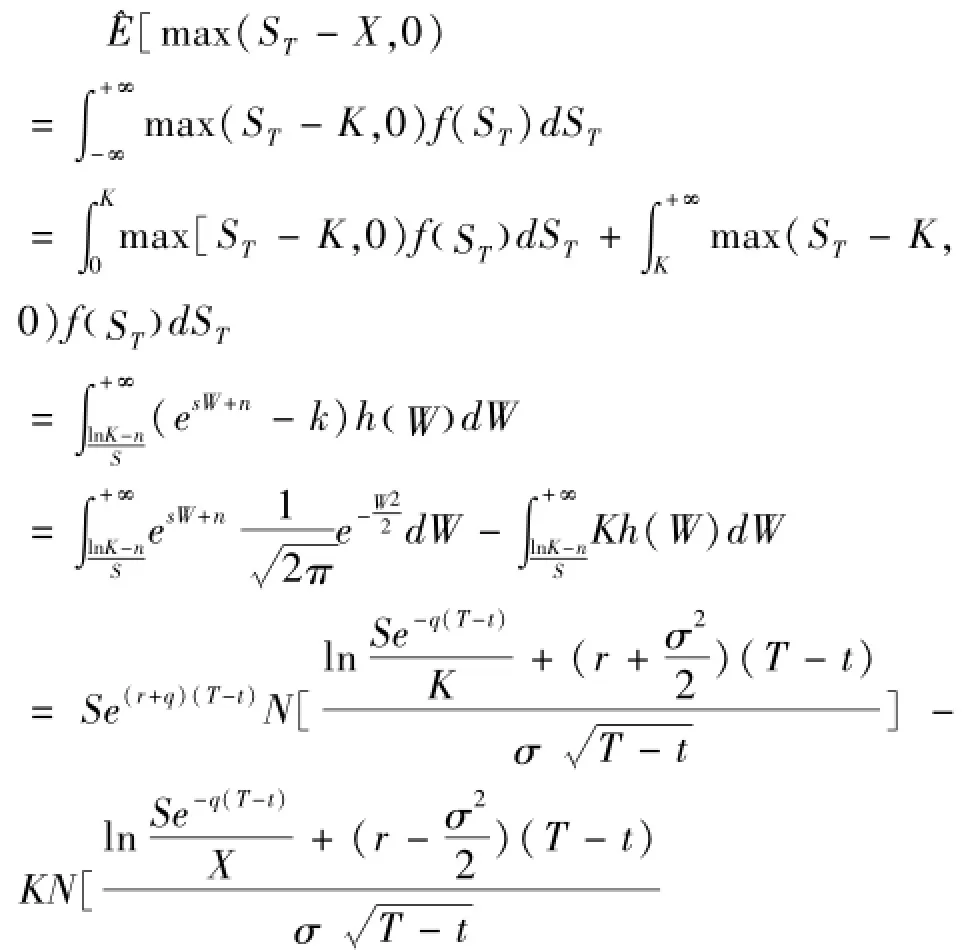
由两者平价关系得p=Ke-r（T-t）N（-d2）-S0e-q（T-t）N（-d1），

其中，

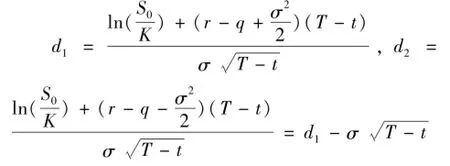
式中S0为t=0时的标的ETF价格，K为合约到期执行价格，r为无风险利率，σ为标的ETF波动率，T-t为期权合约期限，N（x）为正态分布累积分布函数。

3 实证分析与检验

3.1 变量的选取及数据说明

本文采集2015年2月9日至2015年8月20日华夏上证50ETF的每日收盘价作为样本数据，共得到130个样本观察值，数据来源于雅虎财经。此外，通过推导有红利支付的期权定价公式，我们发现期权价格主要取决于以下参数：期初标的ETF价格S0，期权执行价格K，无风险利率r，期权合约期限T-t，标的ETF波动率σ。前三个参数的具体数值我们可以直接得到，无风险利率我们采用一年期的 SHIBOR为3.145%代替，上证50ETF的收益率即股息率为0.04%，2015年8月20日上证50ETF的收盘价为2.361，我们假设期权合约的到期执行价格K为2.20，因此求标的资产的价格波动率成为期权定价中的关键。下面我们将采用历史波动率法和 GARCH模型两种方法来估算波动率σ。

3.2 波动率估计的两种方法

3.2.1 历史波动率法

在期权定价中，波动率是一个极为重要的变量，波动率是指一定时间内连续复利回报率的标准差，通常定义为一年。

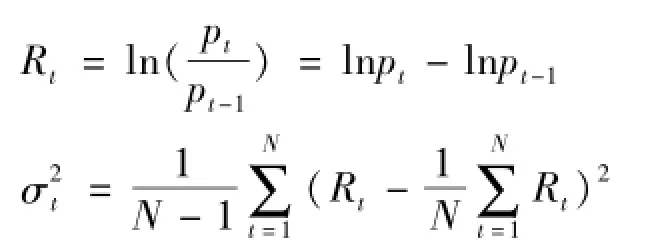
其中，pt为标的ETF每日收盘价格，N为样本数目，σt即为标的ETF的历史波动率。

我们利用MATLAB软件，绘制出华夏上证50ETF收盘价序列和收益率序列的趋势图如图1、图2，从图中可以看出，标的ETF的收盘价不平稳，而收益率序列则是平稳的，数据符合要求。

图1 标的　ETF收盘价趋势图Fig.1 The trend of the underying ETF closing price

图2 标的　ETF收益率趋势图Fig.2 The trend yield underying

因此，使用EVIEWS软件对标的ETF收益率序列进行描述性统计分析，结果如下表1。

表1 描述性统计分析结果Tab.1 The analysis resutt of descriptive statistical

由上表可以看出，标的ETF的历史波动率为0.899195，再使用下述公式将计算出来的日度波动率转化为对应的年度波动率，得到华夏上证50ETF年度波动率为13.93026。

其中σyear为年度波动率，σday为日度波动率，T为股票市场年交易总天数。

3.2.2 GARCH模型法

GARCH模型是指数加权移动平均模型的一种拓展形式，由于时间序列数据可能具有ARCH效应，会因为时间的推移而随着市场环境的改变而改变，而GARCH模型可以解决这一问题，适用范围更加广泛。由于GARCH（1，1）模型是目前所有GARCH模型在实务应用中运用最广泛的一种，我们使用它来估计标的ETF的波动率：

其中，VL为标的ETF长期平均方差，ut-1为标的ETF最近的日变化率，σt即为标的ETF的波动率。

由于时间序列数据通常具有自相关性，横截面数据通常具有异方差性，而GARCH模型的建立要以原序列具有ARCH效应为前提，因此，还要对样本数据回归得到的OLS残差进行ARCH检验。

表2 OLS残差的ARCH检验结果Tab.2 The ARCH tese resuct of ols residue

从表2中可以看出，收益率序列拒绝其残差具有同方差性的假定，证明其ARCH效应显著，表明GARCH模型能够建立。我们使用EVIEWS建立模型，结果如下：

均值方程：Rt=0.004058-0.490567×Rt-1+εt

3.3 实证分析结果及比较

通过历史波动率法和GARCH模型两种方法计算出波动率，至此，期权定价所需参数已全部获得。由此，可以计算出不同波动率下的有红利支付的上证50ETF期权的价格，将计算结果与期权仿真模拟交易的数据比较，发现GARCH模型法在期权定价方面更为准确有效。

表3 上证50ETF期权定价结果Tab.3 The result of the ss 50ETF option pricing

4 结果分析

随着我国在国际上的经济地位越来越高，国家也越来越重视金融市场的逐渐发展和完善，因此鼓励市场推出金融衍生品来调和市场风险。上证50ETF的成功上市和广泛推行更是证明了金融衍生品价格发现和风险规避上的明显优势。为保证其上证50ETF股指期期权市场能够稳健运行，对期权的合理定价和组合设计就成为了大量学者和金融衍生品开发者的关注重心。本文在拓展的B -S模型的基础上，利用两种不同求波动率的方法对上证50ETF期权进行了定价研究。金融衍生品跟市场关系密切，波动较大，为使其更加精确地定价，还需要我们的进一步探索。

参考文献：

［1］宋焕雨.上证50ETF期权定价方法的研究［D］.济南：山东大学，2015.

［2］陈守涛.上证50ETF期权定价研究［D］.苏州：苏州大学，2015.

［3］Black F，Scholes M.The Pricing of Options and Corporate Liabilities.［J］.Journal of Political Economy，1973，81 （3）：637-54.

［4］Hull，White.The Pricing of Options On Assets with Stochastic Volatilities［J］.Journal of Finance，1987，42 （2）：281-300.

［5］Vipul.Box-spread arbitrage efficiency of Nifty index options：The Indian evidence［J］.Journal of Futures Markets，2009，29（6）：544-562.

目：“基于智能遗传算法与支持向量机的生态文明建设体系研究”（项目编号：201510378020）。

朱家明（1973-），男，安徽泗县人，安徽财经大学统计与应用数学学院副教授、硕士。主要研究方向：应用数学与数学建模。

中图分类号：F830.91

文献标识码：A

文章编号：1673-6125（2016）02-0040-04

收稿日期：2015-12-15

基金项目：国家自然科学基金：“基于数据包络分析的环境效率分析评价方法及其应用研究”（项目编号：11301001）；国家级大学生创新项

作者简介：张天凤（1995-），女，安徽阜阳人，安徽财经大学在读本科生。主要研究方向：金融工程。

Based on Shanghai 50 ETF B-S model option pricing research

ZHANG Tian-feng1，ZHU Jia-ming2
（1.Institute of finance，Anhui University of finance&economics，Bengbu 233030 China；
2.School of Statistics and Applied Mathematics，Anhui University of finance&economics，Bengbu 233030 China）

Abstract：For listed Shanghai 50 ETF option pricing problems，with the expansion of the

dividend was derived，Black-Scholes option pricing model，and uses the historical volatility method and GARCH model two kinds of method to calculate the volatility in the option price，introducing volatility model，using MATLAB，EVIEWS software，calculate the different volatility under the condition of the Shanghai 50 ETF option price compared with real data，and found that the GARCH model can make the option pricing results more accurate.

Key words：Shanghai 50 ETF options；option pricing；GARCH model；volatility