基于粒子群优化算法的LS-SVM的GPS高程拟合

高　红, 文鸿雁, 聂光裕, 杨　志, 韩亚坤

(桂林理工大学 a.广西空间信息与测绘重点实验室;b.测绘地理信息学院;c.广西矿冶与环境科学实验中心, 广西 桂林 541004)



基于粒子群优化算法的LS-SVM的GPS高程拟合

高红, 文鸿雁, 聂光裕, 杨志, 韩亚坤

(桂林理工大学 a.广西空间信息与测绘重点实验室;b.测绘地理信息学院;c.广西矿冶与环境科学实验中心, 广西 桂林 541004)

摘要：在GPS高程拟合中，传统拟合方法存在多数据、过学习、泛化能力弱等缺点，导致拟合结果精度欠缺，为此提出了LS-SVM拟合模型。利用粒子群算法对LS-SVM模型的初始参数进行了优化，通过实测数据对该模型进行了分析。实验结果表明，基于粒子群算法优化的LS-SVM模型较传统单一的二次曲面拟合法、BP神经网络、LS-SVM等模型拟合精度高。

关键词：粒子群优化算法;LS-SVM;BP神经网络;二次曲面拟合法;高程拟合

当今, GPS的发展非常迅速, 引出了一个重要的学科问题“GPS高程拟合”, 而在一般的施工过程中, 除了少数的一些工程(如变形监测等)采用大地高系统，大多数情况下需要的是测站点的正常高h而不是大地高H。然而, 要得到正常高h, 需要将大地高H通过一定的模型转换成正常高h[1]。目前最常用的模型有Kriging插值法、支持向量机、BP神经网络法、基于总体最小二乘曲面拟合等方法[2]。而对于大范围且较为复杂的测区, 其拟合出的精度难以达到要求, Kriging插值法、BP神经网络拟合有着较高的精度, 但是两者有一个共同的前提, 就是都需要较多的样本数据, 且BP神经网络容易出现局部最优、过学习等弊端[3-4]。 本文提出的基于粒子群优化算法的LS-SVM模型, 是在LS-SVM模型泛化能力较好、结构简单、全局最优的基础上, 通过粒子群优化算法将LS-SVM模型中的初始粒子参数进行了优化, 从而提高了该模型的预测精度。

1拟合模型

1.1LS-SVM回归预测原理

Suykens和Vandewalb在1999年提出了最小二乘支持向量机[5-6], 其主要思想就是在最基本的支持向量机的基础上, 将最小二乘原理引入其中, 并用等式约束来代替标准支持向量机中不等式约束, 选用数据中的残差值作为训练样本的经验损失, 这样的方法突出了优化问题, 是一个典型的二次规划问题的解决方案。LS-SVM是改进的标准SVM, 解决了线性kkt系统的问题，从而提高了模型的预测速度和精度, 若训练样本集为(xi, yi), i=1, 2, …, n, x∈Rd,y∈R。最小二乘支持向量机回归预测的基本思想是[7-8]:首先通过非线性映射函数φ(x)=(φ(x1),φ(x2), …,φ(xn))将数据映射到高维特征空间, 然后在高维空间构造最优线性决策函数y=wT·φ(x)+b, 通过结构最小化原则, 函数拟合问题可转为下列函数的约束:

优化问题

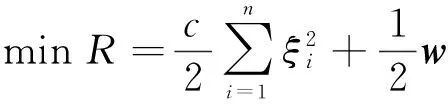
(1)

约束条件为

yi=wTφ(xi)+b+ξi。

(2)

引入Lagrange方法求解这个优化问题:

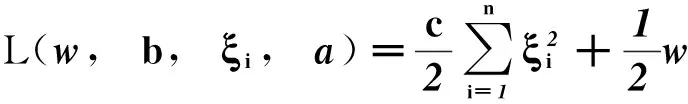
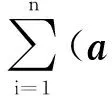
(3)

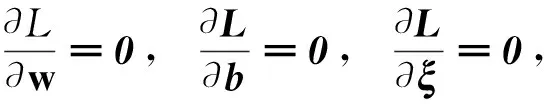
(4)

由以上各式得到LS-SVM函数为

f(x)=ai[φ(xk)φ(xi)]+b。

(5)

为了解决高维计算问题, 引入核函数K(xk, xj)来等效高维空间的内积形式 [φ(xk)φ(xi)],即

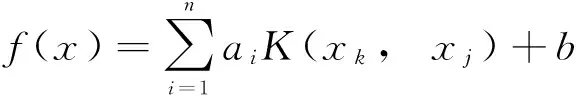
(6)

不同的核函数将生成不同的最小二乘支持向量机, 到目前为止主要的核函数有多项式核函数、Sigmoid核函数和径向基核函数等形式。 考虑到GPS高程拟合预测模型的严重非线性问题, 而且文献[8]中对基于不同核函数的支持向量机进行了一系列的分析以及仿真实验, 发现在支持向量机的回归估计中选择径向基核函数, 其精度优于其他核函数下的支持向量机。 因此, 本文选择RBF向量机函数为核函数进行分析计算。

1.2粒子群优化算法

粒子群算法(particleswarmoptimization,PSO)是由Eberhart和Kennedy在1995年最早提出的一种优化算法。PSO算法是通过不断地迭代更新的种群在一定空间内搜寻最优解,其优化算法的数学模型如下:

假定在一个未知的D维搜索空间中, 由n个粒子组成的种群X=(X1, X2, …, Xn), 而这个种群中肯定存在一个想象中的最优点的解, 将其称之为“粒子”, 该粒子由其速度决定其所在的位置和方向, 导致了其他粒子追随最优粒子在解空间中搜寻, 则有i个粒子群表示为Xi, 该粒子的状态可表示为[8]：

t时刻的位置

(7)

t时刻的速度

(8)

t时刻的个体最优位置

(9)

t时刻的全局最优位置

(10)

则i粒子在t+1时刻的状态为

(11)

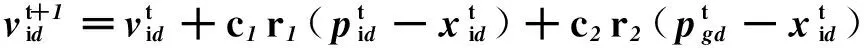
(12)

式中:r1、r2为[0, 1]上的均匀分布随机数,c1、c2为学习因子。

故粒子群算法的流程如图1所示。

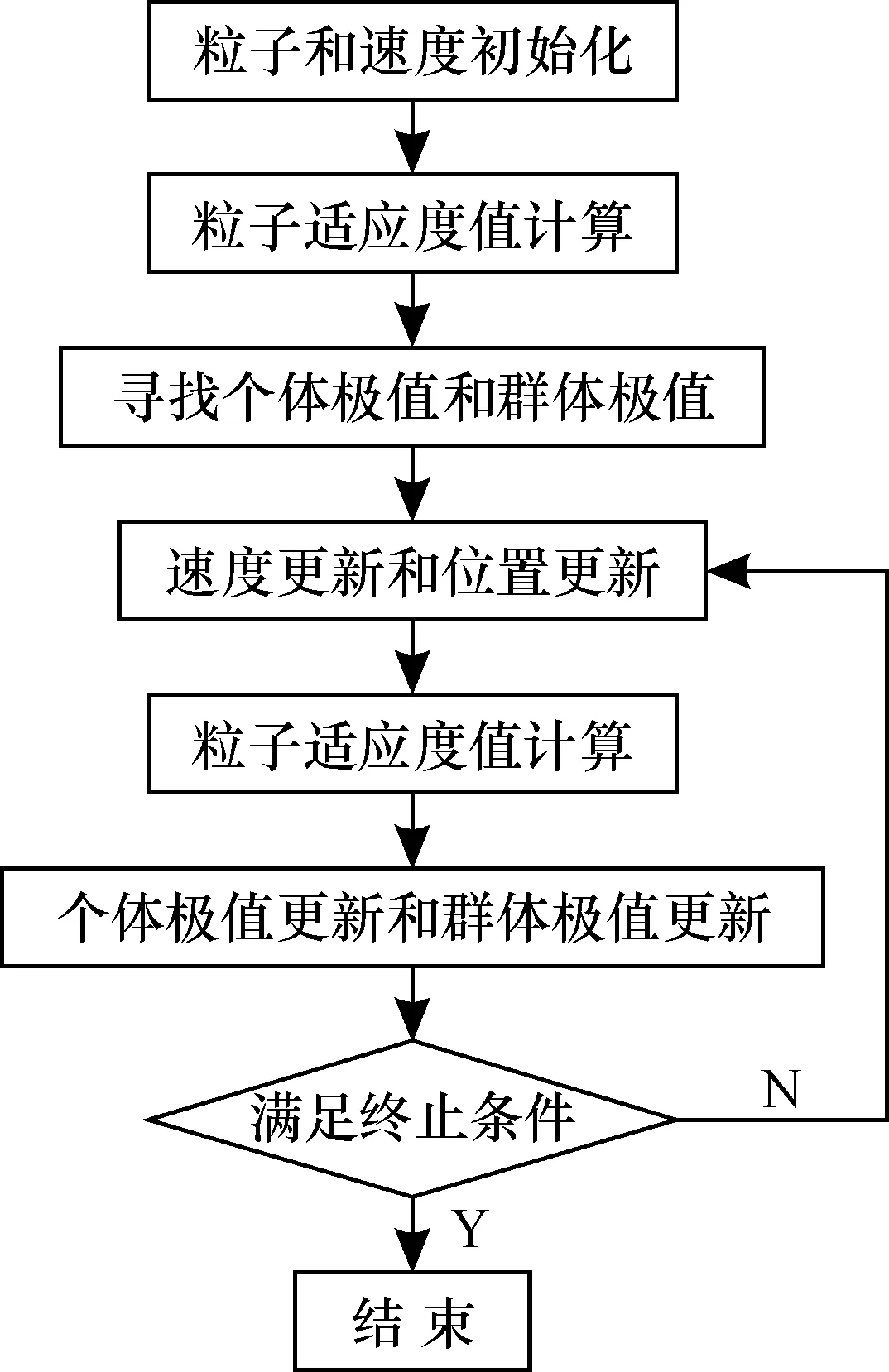
图1　粒子群算法的流程图Fig.1　Flow chart of particle swarm algorithm

2基于粒子群优化LS-SVM

在实际工程项目的应用中都希望能够得到最优的模型解去解决工程问题, 本文建立的是LS-SVM对GPS高程拟合的模型。 为了获得更高精度的模型, 采用粒子群算法的全局搜索能力这一特征对最小二乘支持向量机建模过程中的参数c和g进行优化处理，得到较高精度的LS-SVM模型。粒子群算法优化最小二乘支持向量机的实现过程步骤为:① 采用LS-SVM对训练样本数据进行训练;② 用样本数据训练好的支持向量组建粒子群;③ 产生初速度和粒子数;④ 进行速度更新、种群更新、自适应粒子变异等迭代寻优;⑤ 群体最优更新, 得到新粒子适应度值;⑥ 结果输出。

当迭代次数达到所要求的最大迭代次数或者获得了满足要求的粒子适应函数值时, 终止迭代, 输出结果； 否则，返回继续计算, 直至达到最大迭代次数或获得满足要求的粒子适应值为止。其主要流程见图2。

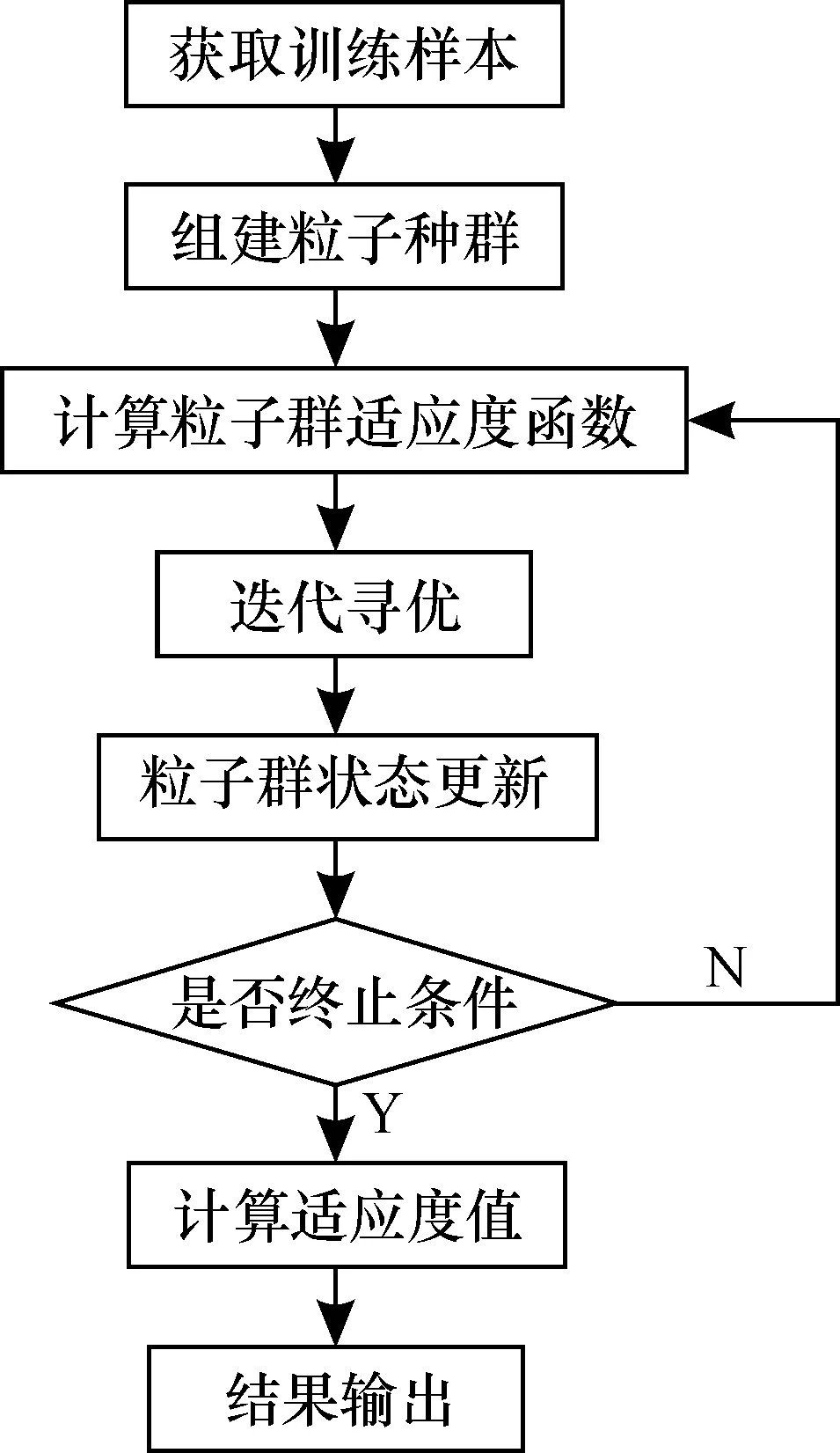
图2　粒子群优化最小二乘支持向量机流程图Fig.2　Particle swarm optimization flow chart of least squares support vector machine

3工程实例

以某高速公路施工测量数据为例，分析粒子群算法优化的最小二乘支持向量机在GPS高程拟合中的应用， 将测量所得的数据整理如表1所示, 选取前7个点作为训练样本, 后6个点作为预测样本。

(1)选取RBF核函数为最小二乘支持向量机的中心核函数。

(2)初始粒子群参数的选取(c1=1.5， c2=1.7， r1、r2选取(0, 1)上均匀分布的随机数, 迭代次数n=300)。

(3)实验分析结果见表2和图3、图4。

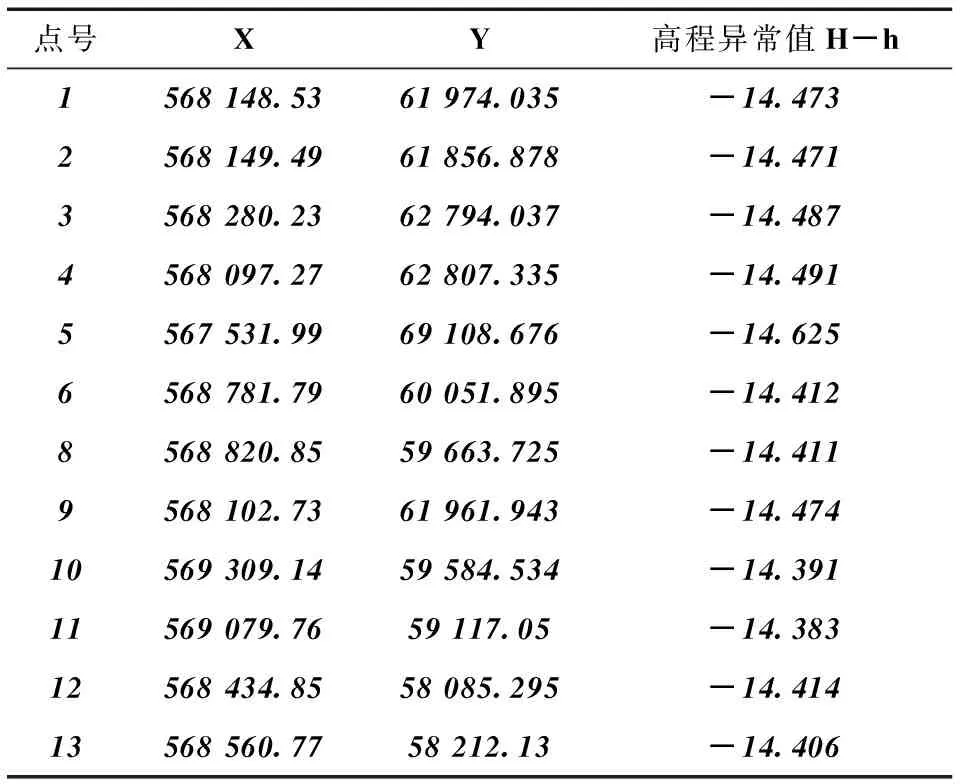
表1　原始测量数据Table 1　Original measurement data 　m

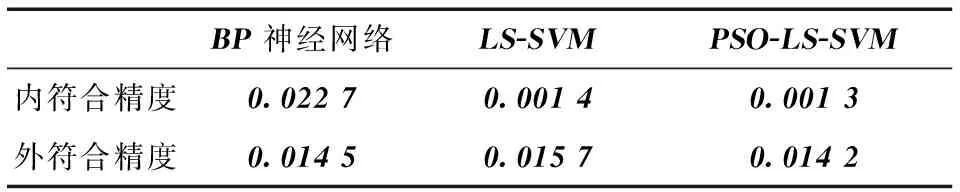
表2　不同模型的符合精度对比Table 2　Precision comparison of different algorithms　　m

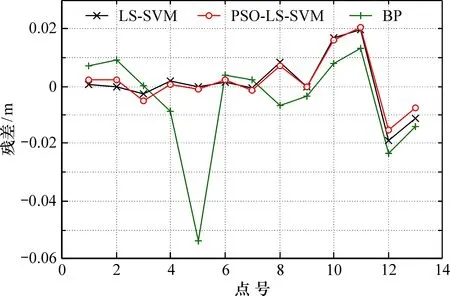
图3　不同模型的残差对比Fig.3　Residual comparison of different algorithms

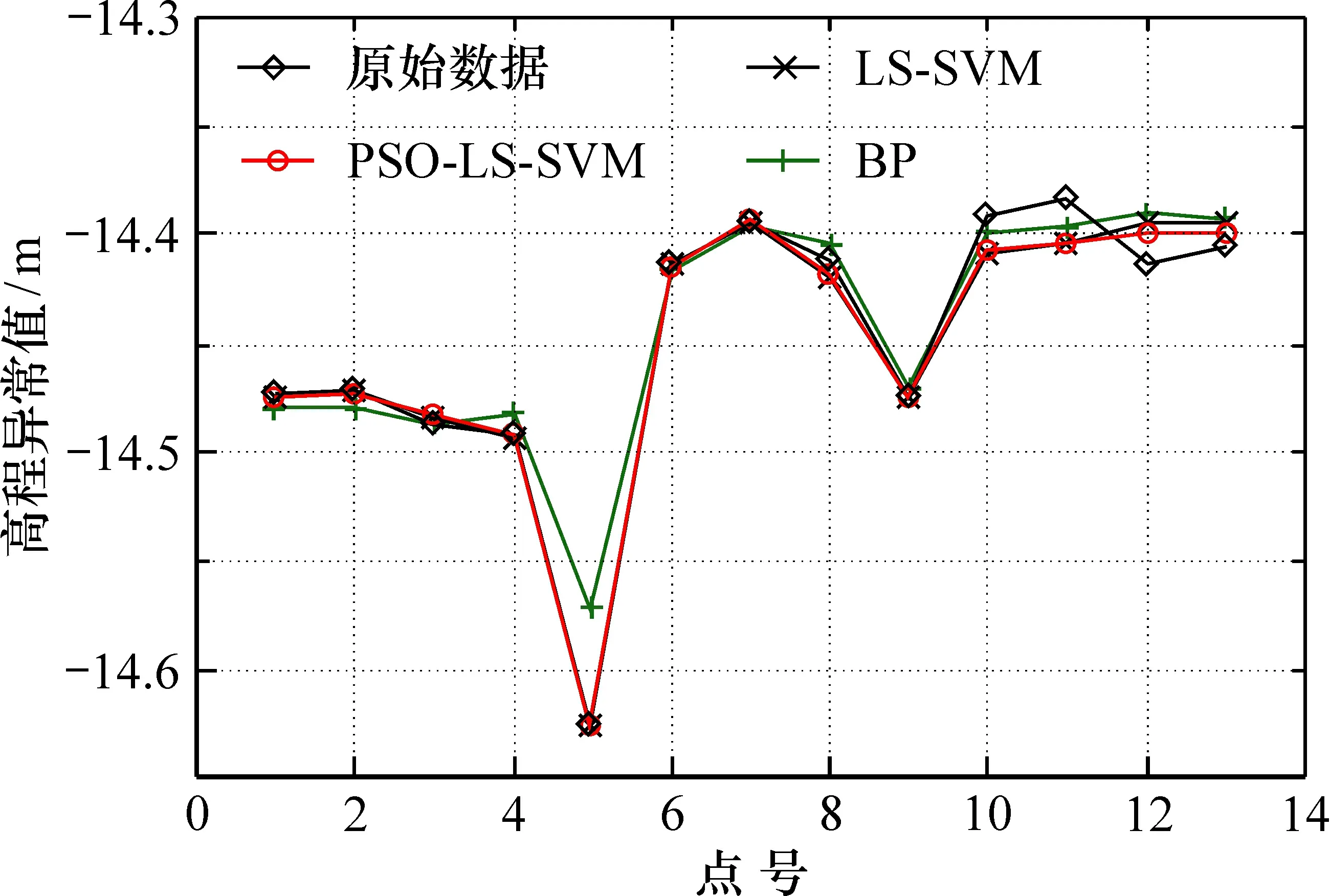
图4　不同模型的拟合对比Fig.4　Fitting comparison of different algorithms

综上可知:通过优化后的最小二乘支持向量机整体精度都有所提高, 最小二乘支持向量机的内符合精度明显优于BP神经网络的精度。由残差对比图3以及拟合对比图4可以明显看到, 各方法效果依次为基于粒子群算法优化的最小二乘支持向量机>最小二乘支持向量机>BP神经网络算法。

4结论

从以上理论和实验中得到以下结论:

(1)最小二乘支持向量机在选择合理的核函数基础上, 对于小样本、非线性的数据有着很好的拟合效果。解决了BP神经网络的局部最优且最小化问题, 同时还克服了BP神经网络的过学习、 样本数量要求过大的难题。

(2)在选择合理的优化方式对最小二乘支持向量机进行优化时,由于粒子群算法基于本身的全局搜索能力, 以及满足局部和全局最优为止的寻优特点, 使得优化后的支持向量机得到的预测结果具有较好的全局最优性，从而解决了BP神经网络易陷入局部最优的缺点, 优化模型有效避免了此问题，提高了拟合模型的整体精度。

参考文献:

[1]侯东阳, 张书毕.基于平面拟合和BP神经网络组合法的GPS高程转换[J].大地测量与地球动力学, 2010, 30(6):91-94.

[2]王小辉, 王琪洁, 丁元兰，等.基于二次曲面和BP神经网络组合模型的GPS高程异常拟合[J].大地测量与地球动力学, 2012, 32(6):103-105.

[3]张昊, 王琪洁，朱建军，等.样本数据预处理对基于BP神经网络的GPS高程拟合的影响[J].大地测量与地球动力学, 2011, 31(2):125-128.

[4]郭春喜, 聂建亮，王斌，等.区域似大地水准面拟合方法及适用性分析[J].大地测量与地球动力学, 2013, 33(1):103-107.

[5]王继刚, 胡永辉.基于最小二乘支持向量机回归综合预测建筑物沉降[J].测绘科学, 2010, 35(3):96-97.

[6]张腾旭, 刘立龙, 周淼，等.基于LS-SVM 和BP神经网络组合模型的GPS高程拟合[J].桂林理工大学学报, 2014, 34(3):505-508.

[7]赵吉文, 刘永斌, 孔凡让, 等.核参数遗传选优的SVM在直线电机建模中的应用[J].系统仿真学报, 2006, 18(12):3547-3549，3553.

[8]徐松金, 龙文.基于粒子群优化最小二乘向量机的地震预测模型[J].西北地震学报, 2012, 34(3):220-223.

[9]万辉, 魏延.一种改进的最小二乘支持向量机算法[J].重庆师范大学学报：自然科学版, 2010, 27(4):69-72.

[10]任超, 吴伟, 黄征凯, 等.基于AIC准则的RBF神经网络在GPS高程拟合中的应用[J].测绘科学, 2013, 38(2):77-79.

文章编号:1674-9057(2016)02-0300-04

doi:10.3969/j.issn.1674-9057.2016.02.017

收稿日期：2015-01-09

基金项目：国家自然科学基金项目(41461089);广西自然科学基金项目(2014GXNSFAA118288);广西“八桂学者”岗位专项经费项目;广西空间信息与测绘重点实验室项目(桂科能151400702;140452402;15-140-07-32);广西矿冶与环境科学实验中心项目(KH2012ZD004)

作者简介：高红(1990—), 男, 硕士研究生, 研究方向:变形监测与数据处理, 827086139@qq.com。

通讯作者：文鸿雁, 博士, 教授, glitewhy@163.com。

中图分类号：P228.4;P224

文献标志码：A

GPS height fitting based on PSO optimizing LS-SVM

GAO Hong, WEN Hong-yan, NIE Guang-yu, YANG Zhi, HAN Ya-kun

(a.Guangxi Key Laboratory of Spatial Information and Geomatics;b.College of Geomatics and Geoinformation;c.Guangxi Scientific Experiment Center of Mining, Metallurgy and Environment, Guilin University of Technology, Guilin 541004, China)

Abstract:In traditional fitting methods there are many shortcomings, such as “multi data, over learning, weak generalization ability”, with less accuracy of fitting results.A method is presented to establish a least squares support vector machine model based on particle swarm optimization algorithm. Through the experimental data accuracy of the analysis to the model,compared with the traditional single model of quadric surface fitting method, the BP neural network, the LS-SVM,the experimental results show that the LS-SVM model has a higher precision based on particle swarm optimization algorithm.

Key words:particle swarm optimization(PSO); LS-SVM;BP neural network;quadric surface fitting; height fitting

引文格式：高红, 文鸿雁, 聂光裕, 等.基于粒子群优化算法的LS-SVM的GPS高程拟合[J].桂林理工大学学报，2016, 36(2):300-303.