纸质平面及空间结构极限承载力试验及结构优化
2016-08-08周诗博
夏 雨,李 靖,周诗博,覃 剑
(广西科技大学 土木建筑工程学院,广西 柳州 545006)
纸质平面及空间结构极限承载力试验及结构优化
夏雨,李靖,周诗博,覃剑
(广西科技大学 土木建筑工程学院,广西 柳州545006)
摘要:通过多组平面及空间纸质结构模型抗压极限承载力试验,分析平面和空间纸质模型破坏形式与机理,研究空间与平面结构型式极限承载力与荷重比随高度、卷杆层数、长宽比等因素的变化规律。试验结果表明:平面结构破坏形态表现为竖向平面外弯曲失稳,空间结构的破坏形态表现为弯扭失稳;通过增加斜向支撑和节点处杆件的厚度不能有效提高结构的极限承载力,但可以提高结构延性,延缓结构破坏的时间;局部加厚竖向构件可以显著延缓结构的破坏速度。
关键词:结构设计大赛;极限承载力;荷重比
国内部分学者对结构竞赛相关方面进行了研究:陈庆军等[1-2]论述了国内外结构建模大赛在高校的发展状况;周克民[3]对一个一等奖优胜作品进行了结构拓扑分析和截面尺寸的分析;顾凌赟等[4]对结构设计竞赛进行了总结;于洋等[5]对结构设计竞赛的模型制作过程和步骤进行了介绍和分析;张炎圣等[6]对桐木结构的桥梁模型进行了计算机模拟并进行了优化。目前缺乏对白卡纸材质平面与空间模型的破坏机理及结构模型优化方面的研究。本文主要针对构件的破坏过程进行试验分析,研究长宽比等因素对白卡纸模型力学性能的影响规律,找出空间模型的优化措施,并用Midas对模型结构进行计算,研究成果为今后结构建模大赛提供一定的建议和参考。
1白卡纸模型的力学性能试验
试验仪器选用SANS液压万能试验机,本试验目的是研究白卡纸平面及空间结构的抗压破坏机理和破坏性能。对于平面结构, 制作5组不同高度
和宽度的平面模型,每组2个模型;对于空间模型,制作不同高度、底面宽度、内径、厚度的8组空间模型,每组各3个模型。模型制作完毕后将其置于试验机上进行加载,加载速度为2 mm/min。待电脑显示的F-S曲线上的力F的值不再增大时,记录相应的极限承载力数值。

图1 平面模型(a)与空间结构(b)的破坏形态Fig.1 Destruction of plane model(a) and spatial model(b)
2试验结果与分析
由表1平面结构的极限承载力与荷重比的试验结果可知平面结构的破坏为:① 各节点处与杆件处并未发生脱胶破坏。此现象表明,刷胶粘接一圈与将杆端磨成弧形凹槽状进行拼接的制作方式足以保证平面结构的节点及杆件的强度;② 平面结构破坏多表现为结构平面外的失稳破坏,不是强度破坏。所以如果要提高其承载力,就要提高杆件平面外的抗失稳能力。破坏机理一般为竖向柱的中部与梁铰接的节点处出现应力集中,在竖向压力与横向拉力的共同作用下发生弯曲失稳。
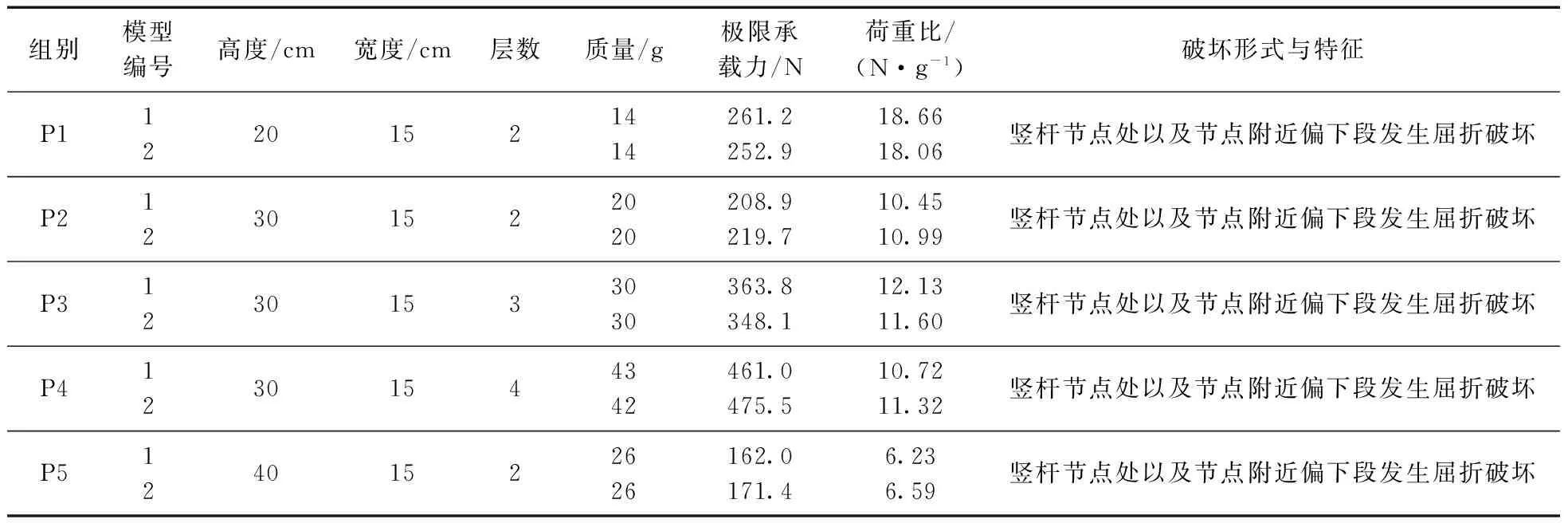
表1 平面结构极限承载力及破坏形式与特征Table 1 Ultimate bearing capacity and destruction modes and characteristics
由平面结构(P3)的力-位移受压曲线图2可知,随着竖向位移的增加其承载力先线性增大到极限承载力,而后迅速下降(斜率变化较大,此阶段是构件破坏的阶段,构件发生严重的变形),之后曲线放缓,承载力逐渐下降。

图2 平面结构P3的力-位移受压曲线Fig.2 Force-displacement curve of the plane structure (P3)
由表2中8组空间结构模型的加载试验数据可知,空间模型的破坏过程为: 加载开始后, 结构逐渐被竖向压缩; 因制作差异, 各竖向构件的极限承载力不同, 局部竖向构件达到受力极限值时出现屈曲破坏, 致使结构因部分失稳产生扭转;随着加载继续, 结构扭转不断加剧, 直至结构完全破坏。 试验中局部竖向构件的屈曲破坏点均位于构件的节点处及其附近段, 且节点处均出现开胶。 其破坏机理:受材料缺陷和制作工艺等影响,在竖向力的作用下其中的一个柱向一侧弯曲, 紧接着对角柱另一侧出现弯曲; 另外一对柱也是如此, 同时梁上的拉力限制其向外侧移动, 导致产生一个扭矩,结构出现扭转失稳破坏。
对于平面结构,在其他影响因素不变的情况下:(1)结构的荷重比随结构高度的增加而减小, 随卷杆厚度(层数)的增大,先增大后减小。在卷杆厚度等于3层的时候出现最大值, 随高度的增加,荷重比呈曲线变化特征(图3)。(2)结构的极限承载力随所用杆件高度的增加而减小, 随卷杆厚度(层数)的增加而增大, 即杆件厚度越大, 极限承载力越大, 并且其变化特征接近线性变化(图4)。
而对于空间结构,在其他影响因素不变的情况下:(1)结构的荷重比随结构高度的增加而减小,随卷杆层数的增大,先增大后减小。在卷杆厚度等于3层的时候出现最大值,且其变化趋势呈曲线变化(图3)。(2)结构的极限承载力随所用杆件高度的增加而减小, 随卷杆厚度(层数)的增加而增大, 即杆件厚度越大,极限承载力越大, 并且随高度呈曲线变化, 随卷杆层数也呈曲线变化(图4)。
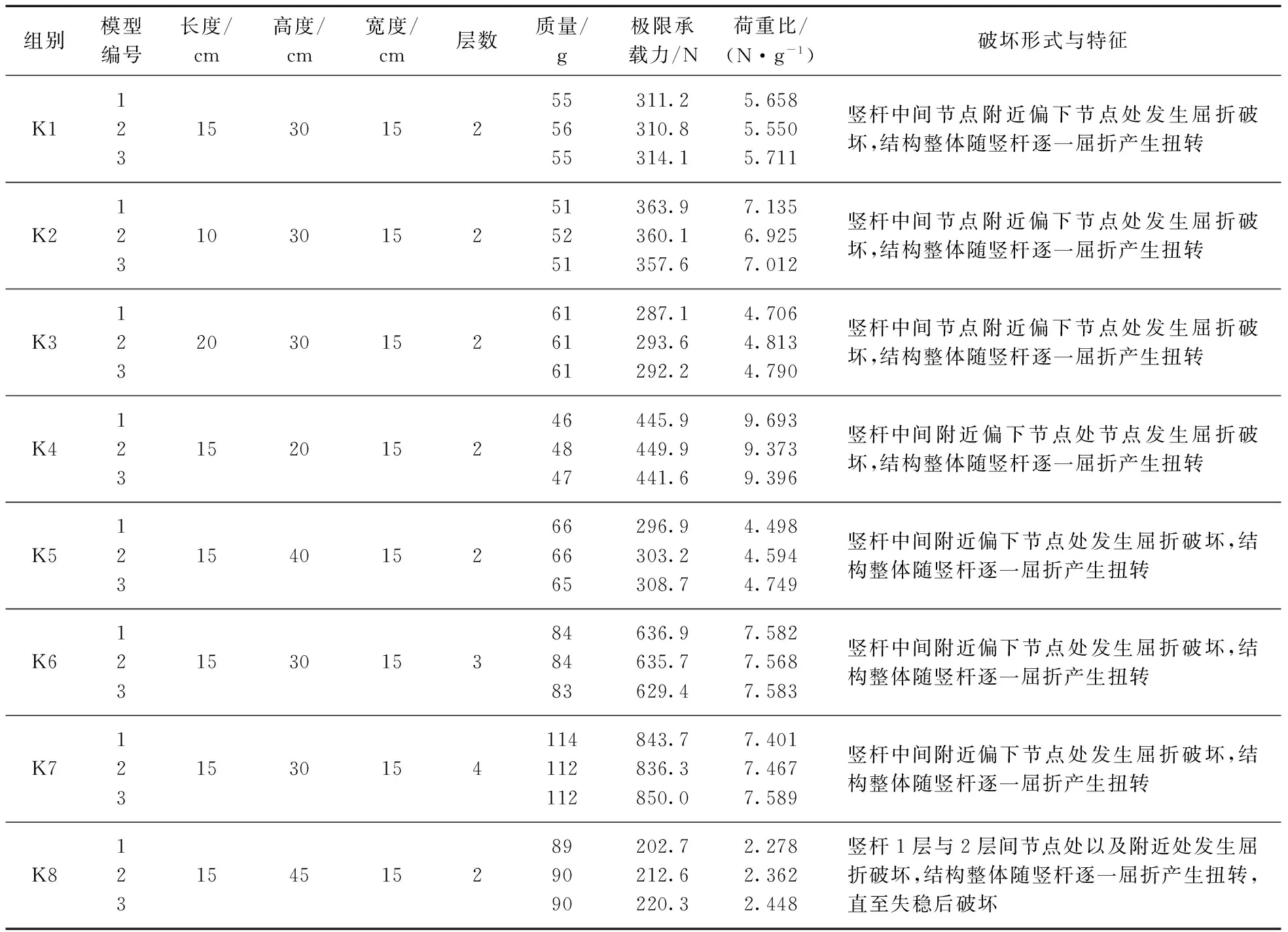
表2 空间结构的极限承载力与荷重比Table 2 Ultimate bearing capacity and load-weight ratio of spatial structure
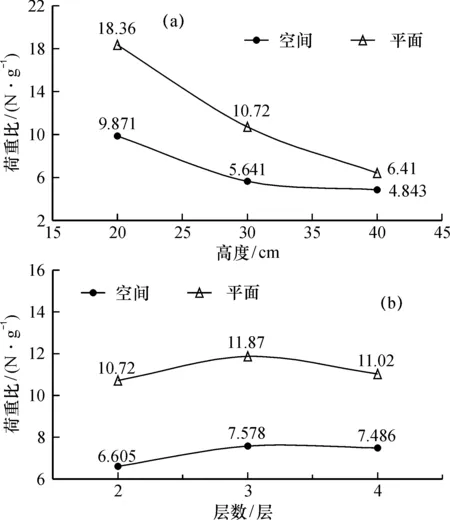
图3 荷重比随高度(a)与卷杆层数(b)的变化Fig.3 Relationship between load-weight ratio and height(a),number of layers(b)

图4 极限承载力随高度(a)与卷杆层数(b)的变化Fig.4 Relationship of ultimate bearing capacity and height(a),number of layers(b)
分析图5可知,在其他影响因素不变的情况下,随着长宽比的增大,空间结构的极限承载力与荷重比都逐渐减小,长宽比越接近零,其极限承载力和荷重比越大。
由图6中空间结构K1的力-位移受压曲线可知,随着竖向位移的增加其承载力先线性增大到极限承载力,而后承载力迅速下降(此阶段是构件破坏的阶段, 构件发生严重的变形, 部分节点发生开胶等现象),之后曲线放缓, 承载力逐渐下降。 由空间优化结构Y2的力-位移受压曲线可知, 随着竖向位移的增加其承载力先线性增大到极限承载力, 之后出现一个波动曲线, 此阶段是优化的支撑对结构稳定性的一个约束的过程。而后承载力缓慢下降达到一个斜率变化最大的区间(此阶段是构件破坏的阶段, 构件发生严重的变形, 部分节点发生开胶等现象),之后曲线放缓,承载力逐渐下降。
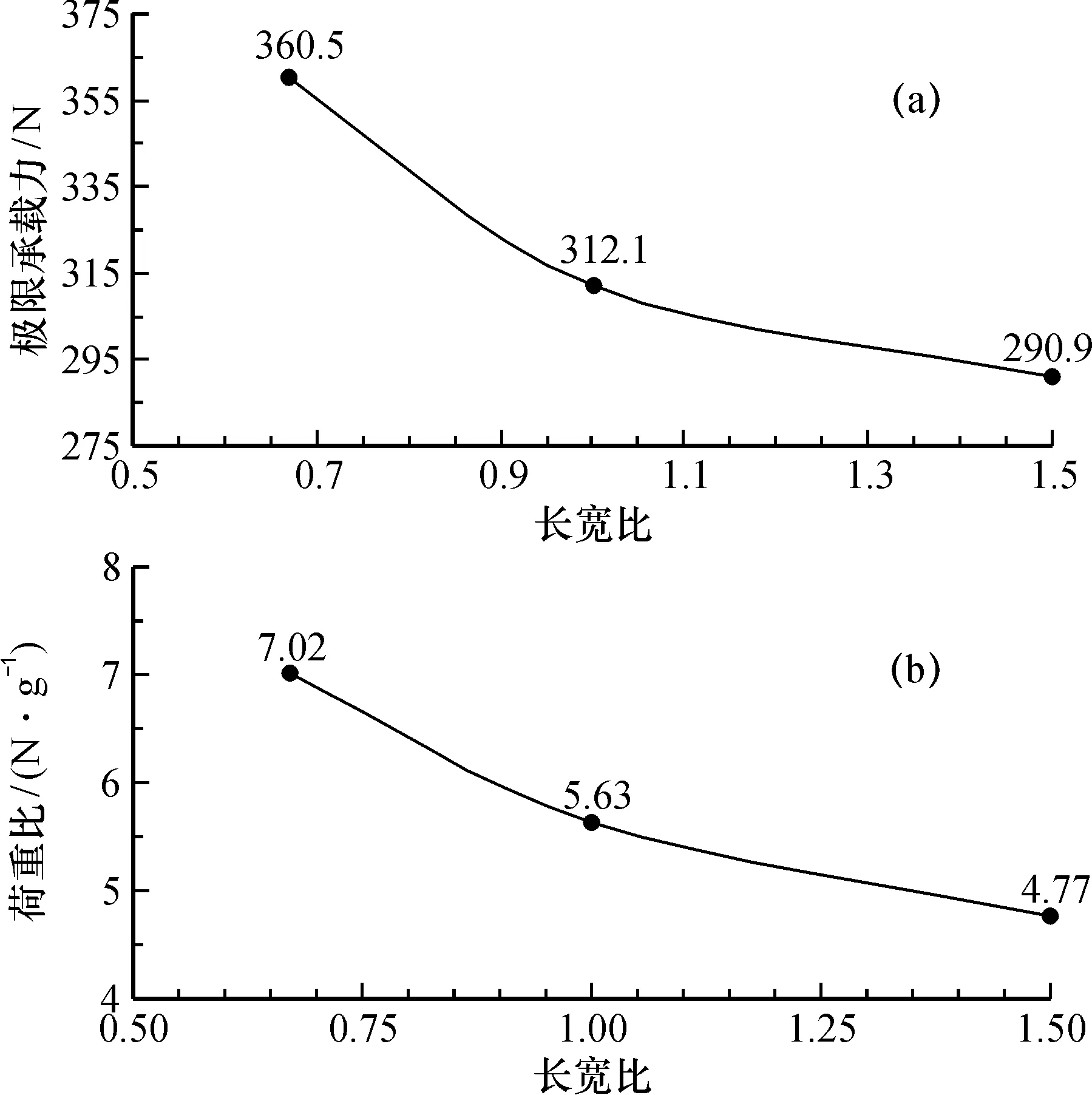
图5 极限承载力(a)与荷重比(b)随长宽比的变化Fig.5 Relationship between ultimate bearing capacity and length-width ratio(a),load-weight ratio and length-width ratio(b)

图6 空间结构K1与优化结构Y2对比曲线Fig.6 Optimization contrast curves of spatial structure K1 and optimizd structureY2
对比两者的受压破坏曲线可以明显得出:优化后的模型在极限承载力最大后,即位移为3~5 mm的波动区段内仍然能够承受一定的力,构件并没有出现大的失稳破坏。没有优化的模型在达到最大承载力时,承载力急剧下降,构件破坏比较快。优化模型受压破坏的时间由原来的60多s提高到130多s,明显提高了结构的延性,有利于提高结构的抗震性能。
根据以上破坏过程可知,结构的破坏薄弱区为竖向构件的中间节点处及其附近段。针对结构破坏薄弱段的特点,本文采取以下两种优化措施:① 在竖向构件中间节点处加斜向支撑构件;② 对竖向构件薄弱段进行加厚。优化后的模型加载破坏形态如图7所示。
由表3优化后的试验结果可知,强化节点处的破坏薄弱区不能有效提高结构的极限承载力, 但能转移结构破坏的部位和降低构件的破坏速度, 即能有效提高结构模型的延性。其中,增大破坏薄弱区厚度的方法更为有效。因此,结构设计竞赛中,应在前期材料性能与结构受力分析的基础上,找出结构的受力薄弱区,再调整结构设计方案与制作方法,以强化受力薄弱区,达到提高极限承载力、提高结构塑性的目的。
由Midas应力图(图8)可以得出,几种优化型式下空间结构失稳破坏的最大应力都是出现在梁柱结合的节点处。上述优化型式不能有效提高结构的极限承载力,加厚柱的中部的应力最小,这是由于加厚柱中柱的刚度变大。加斜撑的应力最大是由于斜向支撑会产生横向剪力导致一定的应力集中。从优化后空间结构破坏过程可以看出,上述优化方法可以有效地提高结构的延性、减缓构件的破坏速度。

图7 优化后的模型加载破坏形态Fig.7 Destruction of optimized models in loading tests
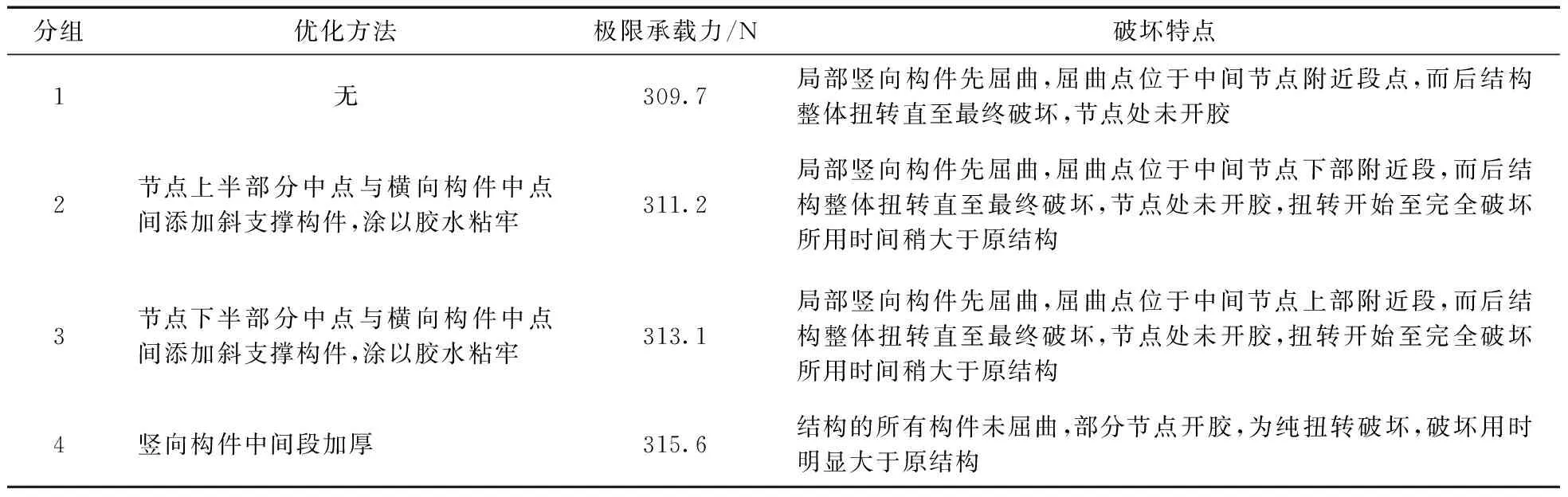
分组优化方法极限承载力/N破坏特点1无309.7局部竖向构件先屈曲,屈曲点位于中间节点附近段点,而后结构整体扭转直至最终破坏,节点处未开胶2节点上半部分中点与横向构件中点间添加斜支撑构件,涂以胶水粘牢311.2局部竖向构件先屈曲,屈曲点位于中间节点下部附近段,而后结构整体扭转直至最终破坏,节点处未开胶,扭转开始至完全破坏所用时间稍大于原结构3节点下半部分中点与横向构件中点间添加斜支撑构件,涂以胶水粘牢313.1局部竖向构件先屈曲,屈曲点位于中间节点上部附近段,而后结构整体扭转直至最终破坏,节点处未开胶,扭转开始至完全破坏所用时间稍大于原结构4竖向构件中间段加厚315.6结构的所有构件未屈曲,部分节点开胶,为纯扭转破坏,破坏用时明显大于原结构
3结论
由试验结果可以得出以下结论:
(1)结构的破坏薄弱区为竖向构件的中间节点处及其附近。
(2)提高竖向构件的破坏薄弱区的受力性能对提高结构的极限承载力作用不大,但能显著延缓结构破坏速度,提高结构的抗震性能,其中增大薄弱区竖向构件的厚度在减小结构破坏速度上最为有效。
(3)平面结构中破坏多表现为结构平面外的弯曲失稳,随着高度的增加,极限承载力和荷重比都在减小,卷杆的厚度为3层时白卡纸结构的荷重比达到最大。
(4)空间结构中多为扭转失稳,结构的极限承载力随构件的高度增加而减小,随卷杆层数的增加而增大, 随结构的长宽比增大而减小; 结构的荷重比随高度的增加而减小,随长宽比的增加而减小,随杆件厚度的增大先增大而后减小,且当卷杆层数为3时空间结构的荷重比达到最大值。

图8 几种优化型式下空间结构的Midas应力图Fig.8 Midas stress diagrams of spatial structure after optimization
参考文献:
[1]陈庆军,王湛,季静,等.第二届全国大学生结构设计竞赛回顾及探索[J].三峡大学学报:自然科学版,2009,31(S):10-12.
[2]陈庆军,罗嘉濠,陈思煌,等.国内外大学生结构设计竞赛总结及研究[J].东南大学学报:哲学社会科学版,
2012,14(S):173-177.
[3]周克民.结构的优化设计分析——大学生结构设计竞赛评述[J].福建建筑,2006(4):28-30.
[4]顾凌赟,殷怡,徐燕,等.全国大学生结构设计大赛研究与竞赛指导初探[J].中国电力教育,2011(23):131-132.
[5]于洋,姜峰,司炳君,等.关于结构设计竞赛中模型的设计与制作方法[J].科技资讯,2007,18(2):201-202.
[6]张炎圣,陆新征.大学生结构设计大赛中的计算机仿真分析[J].力学与实践,2009,31(4):110-112.
文章编号:1674-9057(2016)02-0247-06
doi:10.3969/j.issn.1674-9057.2016.02.008
收稿日期:2014-10-09
基金项目:国家自然科学基金项目(51569005);广西自然科学基金项目(2015GXNSFAA139279); 广西高等学校科研项目(201203YB130);广西研究生教育创新计划项目(JGY2013054;YCSZ2015207);地方高校国家级大学生创新创业训练计划项目(201510594006);广西大学生创新创业培训计划项目
作者简介:夏雨(1979—),男,博士,副教授,土木工程专业,summ-rain@163.com。
中图分类号:TU317.2;TU312
文献标志码:A
Ultimate bearing capacity test and structure optimization on paper-made plane and spatial structures
XIA Yu, LI Jing, ZHOU Shi-bo, QIN Jian
(College of Civil Engineering and Architecture,Guangxi University of Science and Technology,Liuzhou 545006,China)
Abstract:Tests on several groups of paper-made plane and space structures are done to analyze the failure mode and mechanism,and how structure height, thickness and slenderness ratio can affect the ultimate capacity and load-weight ratio. Results show that plane structures usually lose stability out of plane. And spatial structures turn out flexural-torsional buckling modes when it reaches the ultimate capacity. It can’t improve the structure capacity obviously by locally strengthening, but it can make structure ductile, especially with the method of local thickening.
Key words:structure design competition;ultimate bearing capacity;length-width ratio
引文格式:夏雨,李靖,周诗博,等.纸质平面及空间结构极限承载力试验及结构优化[J].桂林理工大学学报,2016,36(2):247-252.
