相邻桥跨对大跨钢桁梁桥-轨道系统的影响*

于向东　尹兴权　闫斌†

(1.中南大学 土木工程学院， 湖南 长沙 410075； 2.中铁工程设计咨询集团有限公司 桥梁工程设计研究院, 北京 100055)



相邻桥跨对大跨钢桁梁桥-轨道系统的影响*

于向东1尹兴权2闫斌1†

(1.中南大学 土木工程学院， 湖南 长沙 410075； 2.中铁工程设计咨询集团有限公司 桥梁工程设计研究院, 北京 100055)

采用非线性弹簧模拟无缝线路纵向阻力，用带刚臂的梁单元模拟梁体，以黄韩侯铁路线上某156m简支钢桁梁桥为例，分析相邻桥跨结构对大跨度简支钢桁梁桥上无缝线路纵向力分布规律的影响，提出相关参数的取值建议.研究表明：分析大跨简支钢桁梁桥上无缝线路纵向力时，两侧的多跨简支梁在下部结构纵向刚度相差较小的情况下可按6跨进行简化；与32m标准跨度相比，相邻简支梁跨度为24m时固定端伸缩力降低了9%，40m时固定端伸缩力增大了7%；相邻桥跨为大跨连续梁时，钢桁梁固定端伸缩力增大了2.2倍，全桥伸缩压应力最大值增大了12%；在连续梁与钢桁梁之间布置1跨或2跨简支梁可大幅降低钢桁梁固定端的钢轨应力；在钢桁梁桥上设置小阻力扣件可使伸缩工况下钢桁梁的钢轨应力最大值和桥墩水平力显著减小.

铁路桥梁；轨道工程；大跨度钢桁梁桥；相邻桥跨；小阻力扣件

在温度、活载和列车制动作用下，桥梁与钢轨之间发生相对位移，由于桥梁与无缝线路间存在纵向非线性约束，桥梁与钢轨之间将产生复杂的相互作用.国内外学者已针对该问题进行了广泛研究[1- 5]，涉及的桥梁形式包括标准简支梁、连续梁[6]、大跨度斜拉桥[7]等，相关规范还明确了高速铁路标准跨度简支梁桥上无缝线路的检算方法[8- 10].与以上桥梁不同，客货共线铁路大跨度简支钢桁梁桥具有跨度大、荷载重、施工周期短等特点[11]，国内外研究和实践相对较少，大跨简支钢桁梁桥上无缝线路纵向力的分布规律仍不明确.

文中以黄韩侯铁路线上某156m简支钢桁梁桥为例，采用非线性弹簧模拟线路纵向阻力，建立了考虑相邻桥跨和路基结构的轨-梁-墩一体化空间有限元模型，研究了相邻桥跨数量及结构形式对大跨简支钢桁梁桥上无缝线路纵向力分布规律的影响，并提出相关参数的取值建议.

1　大跨简支钢桁梁计算模型与参数

忽略轨枕变形和支座摩阻力，在桥梁两侧路基上各建立一定长度的钢轨来减少边界条件的影响[12]，轨道采用梁单元模拟，主梁采用带刚臂的梁单元模拟.

建立如图1所示的简支梁桥-轨道系统有限元模型，以文献[10]中附录C.2算例验证计算模型的正确性.

经计算，文中计算结果与UIC算例[10]计算结果相差0.59%～8.72%：简支梁固定支座处钢轨应力最大相差2.50%，墩顶水平力最大相差8.72%，滑动支座处钢轨应力最大相差4.35%.证明所建立的梁轨相互作用模型可正确分析桥上无缝线路纵向力.

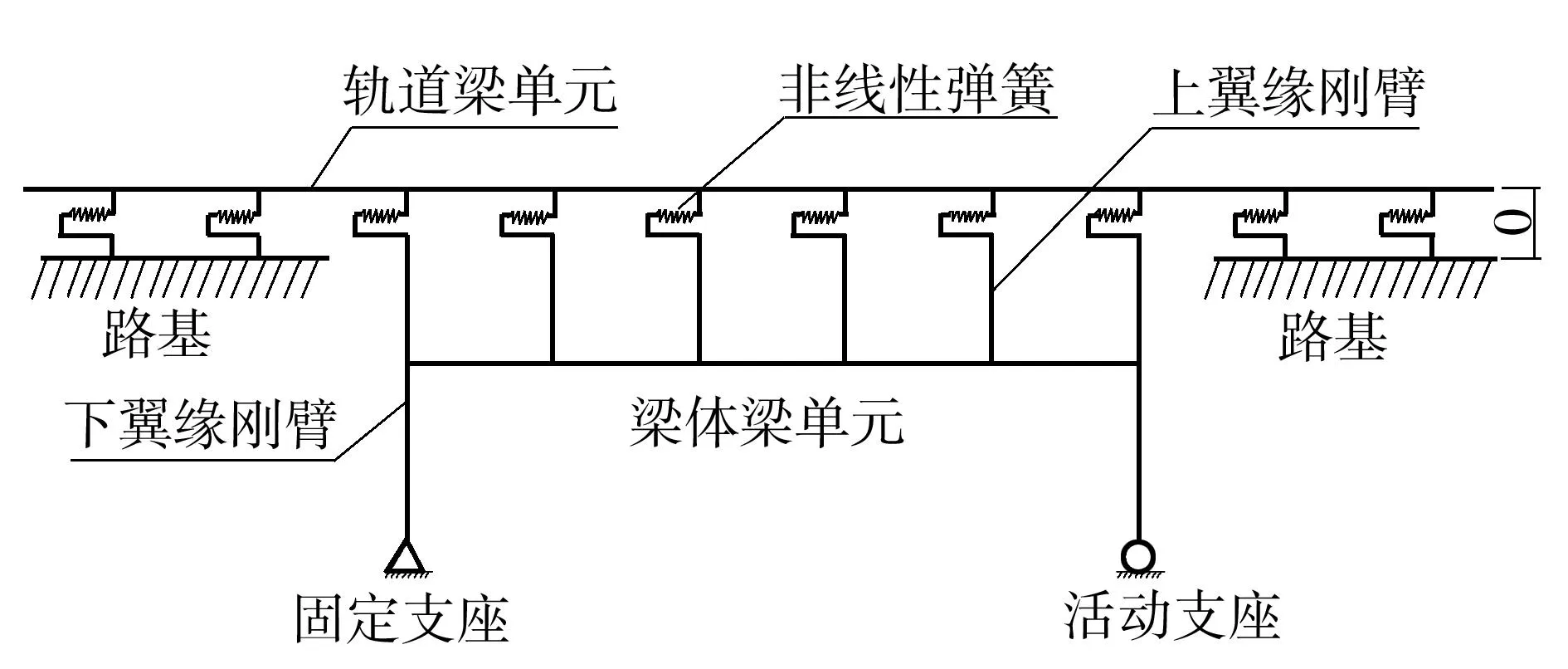
图1　简支梁桥-轨道系统有限元模型示意图

Fig.1Schematicdiagramoffiniteelementmodelofrailwaytrack-bridgesystem

以黄韩侯铁路线上某156m简支钢桁梁为工程背景进行分析.简支钢桁梁桁高17.0m，桁宽8.6m，节间距为14.1或14.2m，纵梁设置两处断开.其相邻桥梁为24、32m标准简支T梁及(40+4×64+40)m变截面连续箱梁，梁高2.9 ～5.3m.桥墩高5～16m.桥上铺设单线有砟轨道，CHN60型钢轨.线路纵向阻力模型采用分段线性理想弹塑性模型，相关参数参考规范TB10015—2012[8]按式(1)-(2)取值.

有砟轨道道床纵向阻力：

(1)

采用弹条V型小阻力扣件的纵向阻力：

(2)

式中，r为线路纵向阻力，u为梁轨纵向相对位移.

台顶纵向水平线刚度取为150MN/m，制动墩墩顶纵向水平线刚度均取为100MN/m.

计算钢轨伸缩力时，钢桁梁整体升温25 ℃，混凝土梁升温15 ℃.计算挠曲力时，桥梁设计标准活载采用中-活载，分机车下和车辆下两段等效均布加载于梁体单元上.计算制动力时，轮轨粘着系数取为0.164[8].

2　大跨简支钢桁梁桥-轨道系统受力分析

2.1钢轨纵向力

建立如图2所示的有限元模型.桥梁两侧路基上各建立200m长钢轨，简支钢桁梁采用明桥面空间模型，桁架各杆件及桥面系纵、横梁均用空间梁单元模拟，构件之间连接为刚接.相邻简支梁、连续梁用带刚臂的梁单元模拟.采用非线性弹簧单元模拟梁轨间的纵向连接，梁轨间在竖向为刚性连接.制动墩采用具有等效刚度的线性弹簧模拟[11]，墩底固结，如图3所示.分别计算钢轨伸缩力、挠曲力和制动力.

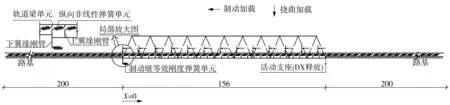
图2　有限元模型及加载示意图(单位：m)

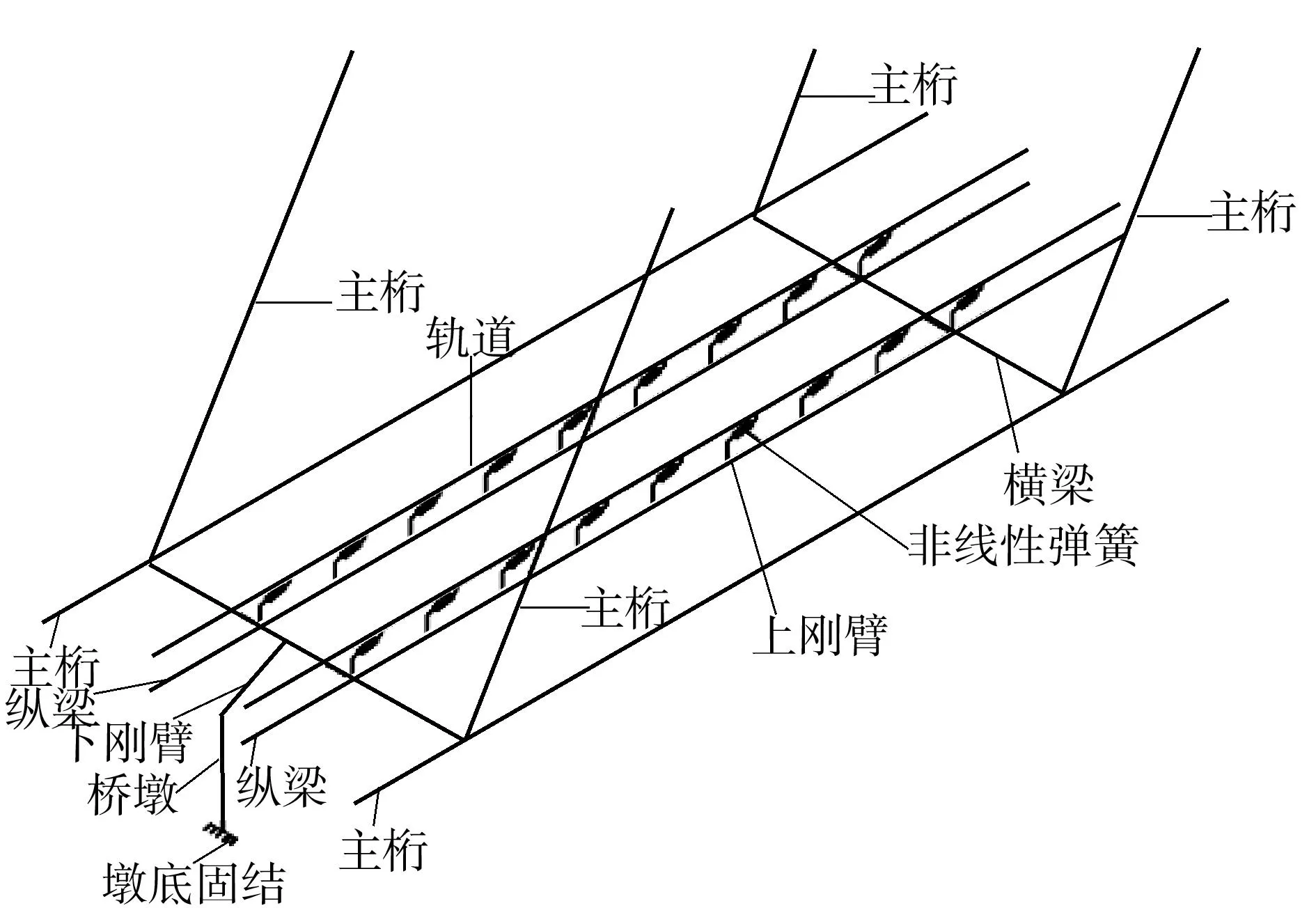
图3　钢桁梁空间有限元模型

计算结果显示，根据文献[8]，控制本桥无缝线路钢轨强度检算的钢轨伸缩应力为47.9MPa(拉)，钢轨制动应力为48.3MPa(拉)，稳定性检算应考虑伸缩力(压)和挠曲力(压)中较大者，为84.5MPa.

2.2路基段钢轨加载长度的影响

考虑路基段加载长度分别为0、20、40、60、80、100、140和200m的情形，计算制动工况下的钢轨应力和桥墩水平力，结果见图4.

由图4可知，计算制动力时路基段加载长度只在一定范围内影响钢桁梁桥-轨道系统的受力和变形规律.与不考虑路基段加载[13]情况相比，路基段加载长度为80m时，钢轨制动应力最大值增大了8%，桥墩水平力增大了11%.超过80m后，钢桁梁段钢轨制动力和桥墩水平力不再随加载长度的增大而变化.

图4　路基段加载长度的影响

3　相邻桥跨布置形式的影响

3.1相邻简支梁跨数的影响

在钢桁梁两侧各布置1-7[14]跨32m标准简支T梁，分析桥上无缝线路纵向力变化规律，结果见图5.

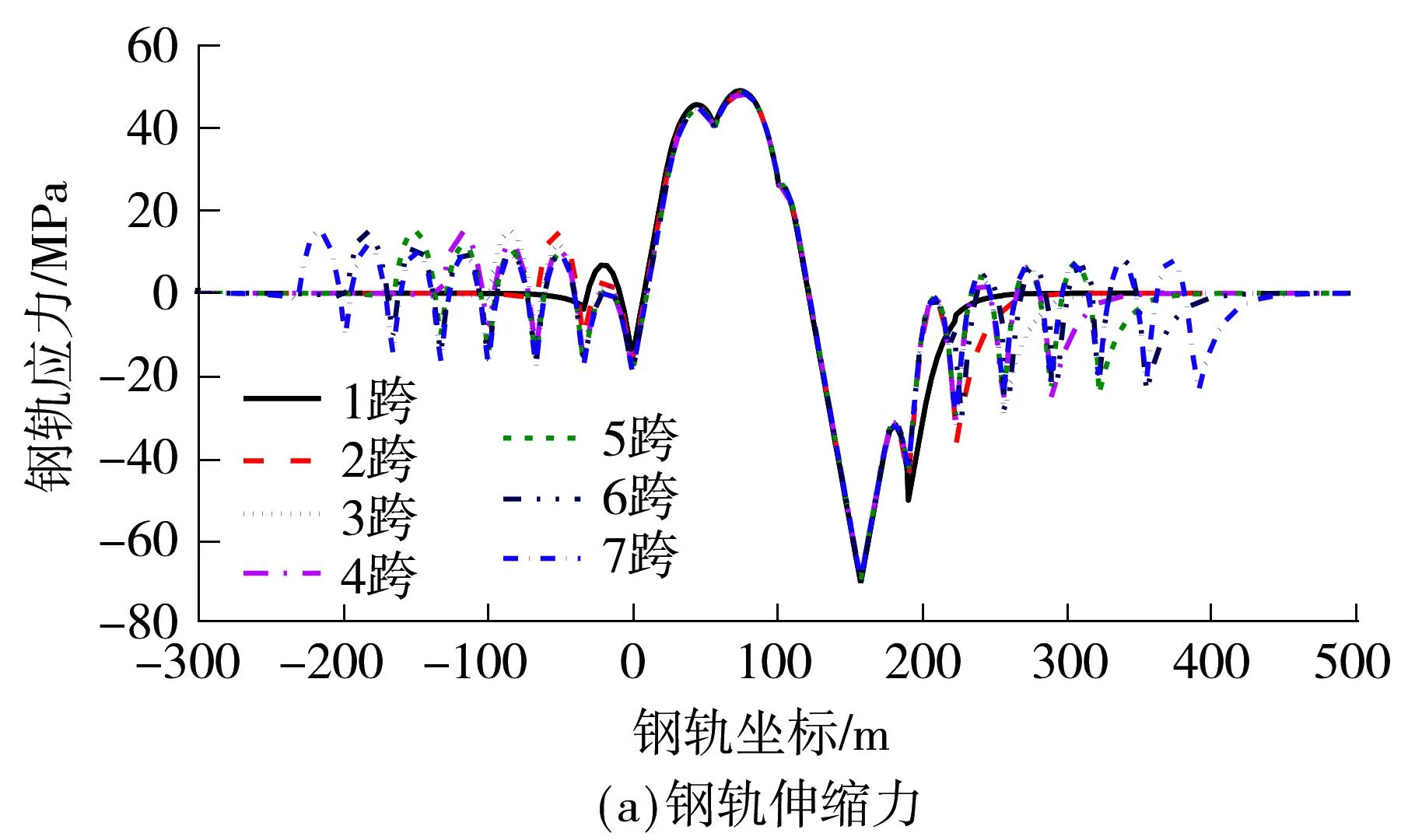
图5　相邻简支梁跨数的影响

计算挠曲力时，按照规范TB10015—2012[8]规定，在钢桁梁和相邻一跨简支梁上布置荷载；计算制动力时，加载范围同挠曲力，列车从右侧入桥并在桥上制动.

相邻简支梁跨数对钢桁梁固定端钢轨纵向力影响较大.当简支梁跨数超过4跨后，固定端钢轨纵向力趋于定值，伸缩应力为19.3MPa(压)，较1跨时增大了25%；挠曲应力为13.6MPa(拉)，较1跨时减小了18%；制动应力为49.5MPa(压)，较1跨时减小了4%.超过6跨后，全桥钢轨纵向力不再变化.因此，在分析大跨简支钢桁梁桥上无缝线路纵向力时，两侧的多跨简支梁在下部结构刚度相差较小时可按6跨进行简化.

3.2相邻简支梁跨度的影响

在实际工程应用中，多跨简支梁单跨跨度一般取32m，24m或40m简支梁用于调跨.本节对图6所示两种桥跨布置方案下大跨简支钢桁梁桥上的无缝线路纵向力进行对比分析，结果见表1.

图6　调跨布置方案(单位：m)

相邻简支梁跨度/m钢轨纵向力/MPa固定支座端滑动支座端伸缩力挠曲力制动力伸缩力挠曲力制动力伸缩力最大值/MPa拉压32-19.313.6-49.5-69.4-18.934.848.869.424-17.613.7-51.1-69.0-18.934.249.069.040-20.613.3-48.6-69.7-19.035.148.769.7

可见，随相邻简支梁跨度的增大，钢桁梁固定端伸缩力逐渐增大，挠曲力和制动力逐渐减小，滑动端伸缩力、挠曲力和制动力均逐渐增大.与32m标准跨度相比，24m跨度时固定端伸缩力降低了9%，40m跨度时固定端伸缩力增大了7%.

规范TB10015—2012[8]指出，单线墩台设计纵向力取伸缩力、挠曲力的较大值，本桥取伸缩力.相邻简支梁跨度对伸缩力最大值的影响范围不超过1%，因此，在对钢桁梁桥墩进行纵向力检算时，可忽略相邻简支梁因调跨而采用不同形式的影响.

3.3相邻大跨连续梁的影响

参考新黄河大桥原设计，在钢桁梁和简支梁之间布置1孔(40+4×64+40)m连续梁，如图7所示，并建立用10跨32m简支梁代替该连续梁的10跨简支梁模型作为对比，结果见图8.

可见，相邻大跨连续梁对大跨简支钢桁梁桥上无缝线路伸缩力的分布规律影响较大.与10跨简支梁布置相比，考虑相邻大跨连续梁后，钢桁梁固定端伸缩力增大了2.2倍，全桥伸缩压应力最大值增大了12%，拉应力最大值减小了4%.在进行钢桁梁桥上无缝线路纵向力分析时，相邻大跨连续梁不能用多跨标准简支梁代替.

图7　相邻大跨连续梁布置方案(单位：m)

Fig.7Arrangementofadjacentlong-spancontinuousbeam(Unit：m)

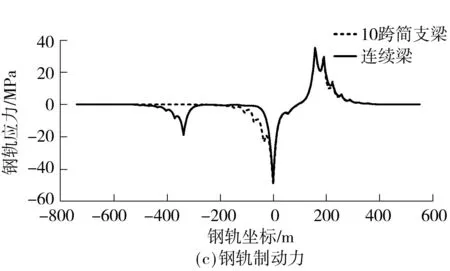
图8　相邻大跨连续梁的影响

3.4连续梁与钢桁梁间简支梁跨数的影响

在连续梁和钢桁梁之间布置一定跨数的标准简支梁，可减小连续梁对钢桁梁固定端钢轨应力的影响.文中在连续梁和钢桁梁之间布置1-6跨32m简支梁，分别对其钢桁梁上无缝线路纵向力分布规律进行分析，结果见图9.

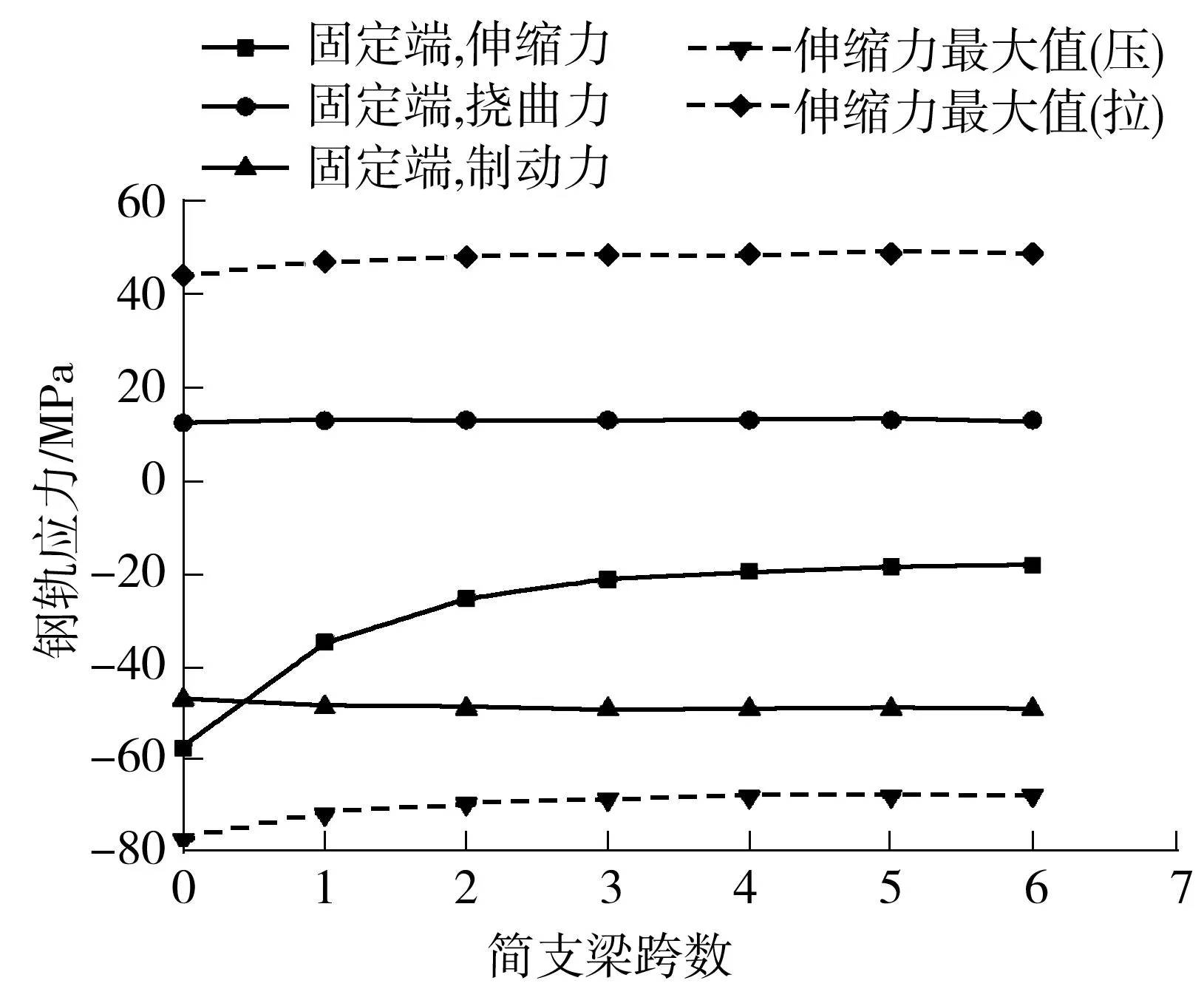
图9　连续梁和钢桁梁间简支梁跨数的影响

Fig.9Influenceofspannumberofbeambetweensteeltrussgirderandlong-spancontinuousbeam

与图7所示的连续梁与钢桁梁直接相连的布置相比，插入1跨32m简支梁时，伸缩压应力最大值降低了7%，拉应力最大值增大了7%，固定端钢轨伸缩力降低了40%，挠曲力增大了4%，制动力增大了3%.插入简支梁跨数超过2跨后，钢桁梁桥上无缝线路纵向力基本不再变化.

综上所述，当大跨连续梁与钢桁梁相邻布置时，可在连续梁与钢桁梁之间布置1跨或2跨标准简支梁，以降低相邻大跨连续梁对钢桁梁桥上钢轨伸缩力的不利影响.

4　小阻力扣件和钢轨伸缩调节器的设置方案

工程中通常采用小阻力扣件和设置钢轨伸缩调节器来减小钢轨所受纵向力[15].文中以在连续梁和钢桁梁之间插入1跨32m简支梁桥跨布置方案为基础，选取图10中所示几种典型无缝线路布置方案，探讨小阻力扣件和钢轨伸缩调节器对钢桁梁桥上钢轨纵向力的影响规律.其中，小阻力扣件采用理想弹塑性非线性弹簧模拟，见式(2).钢轨伸缩调节器采用钢轨节点断开模拟.

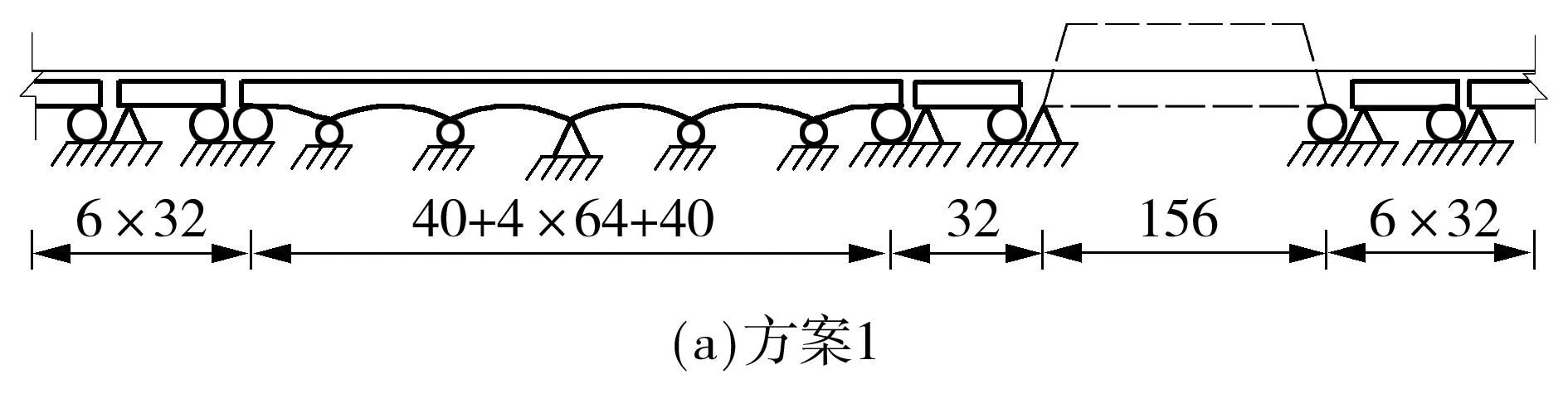
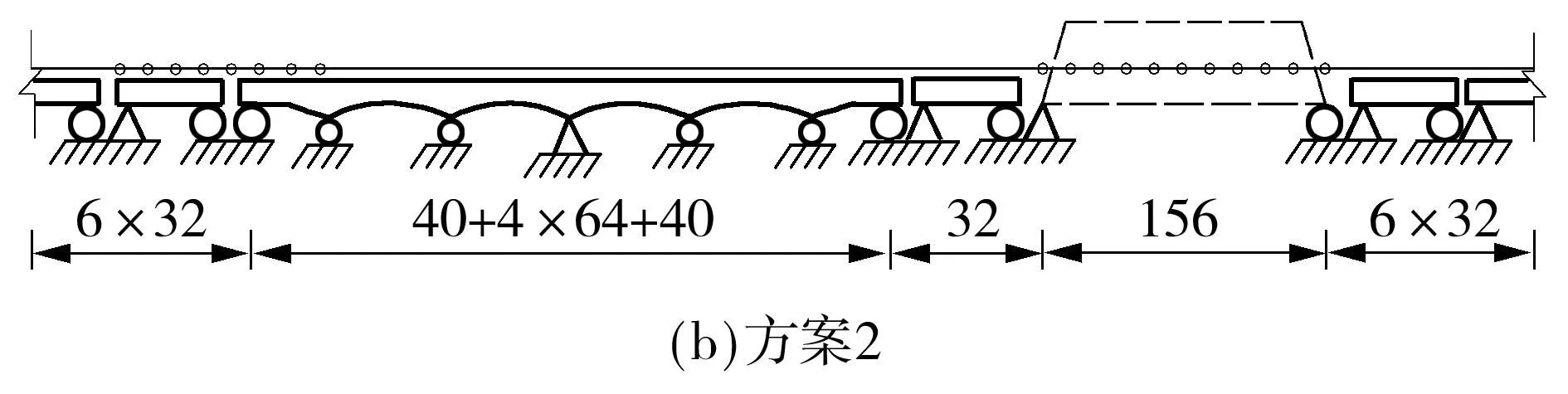
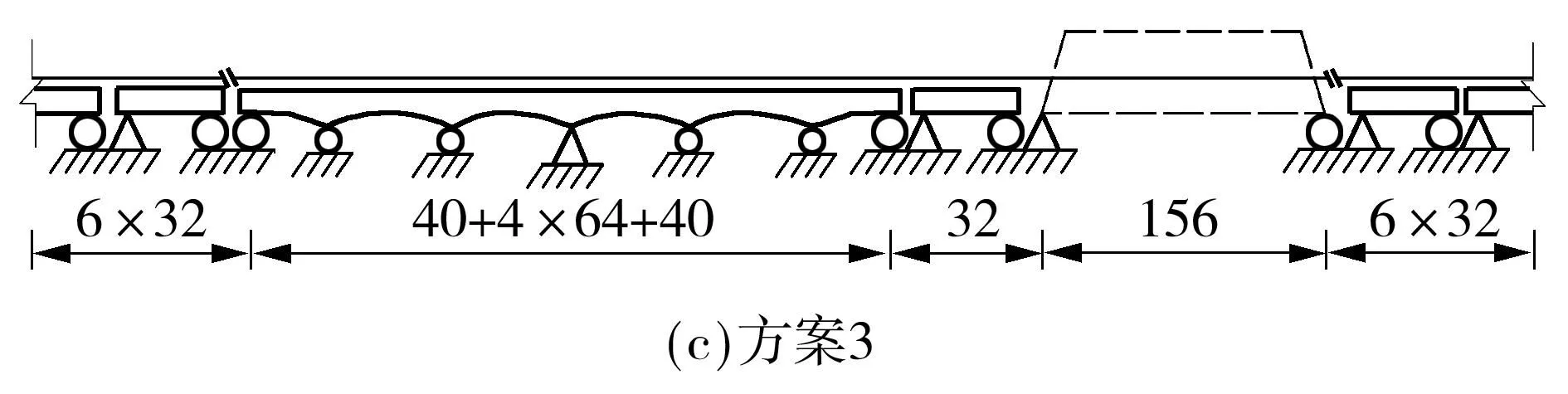
图10　无缝线路布置方案(单位：m)

分别计算各方案中伸缩工况和制动工况下钢轨纵向力、桥墩水平力和钢轨伸缩调节器处钢轨的相对位移.伸缩工况计算时考虑梁体整体升温和整体降温两种情况，制动工况计算时考虑列车左侧入桥和右侧入桥两种情况，见图11、12.

由图11(a)可知，与方案1相比，方案2中连续梁和钢桁梁左、右两端及钢桁梁跨中等几处峰值应力均显著减小，全桥钢轨伸缩力最大值降低了27%.方案3和4中钢轨伸缩调节器附近的钢轨伸缩力大幅降低，且连续梁右端与简支梁相接处的钢轨伸缩力降低了约38%，钢桁梁固定端钢轨伸缩力降低了约80%.由图11(b)可知，与方案1相比，方案2计算结果显示仅设置小阻力扣件对钢轨制动力影响较小，方案3和4中钢轨制动力最大值增大了约20%.

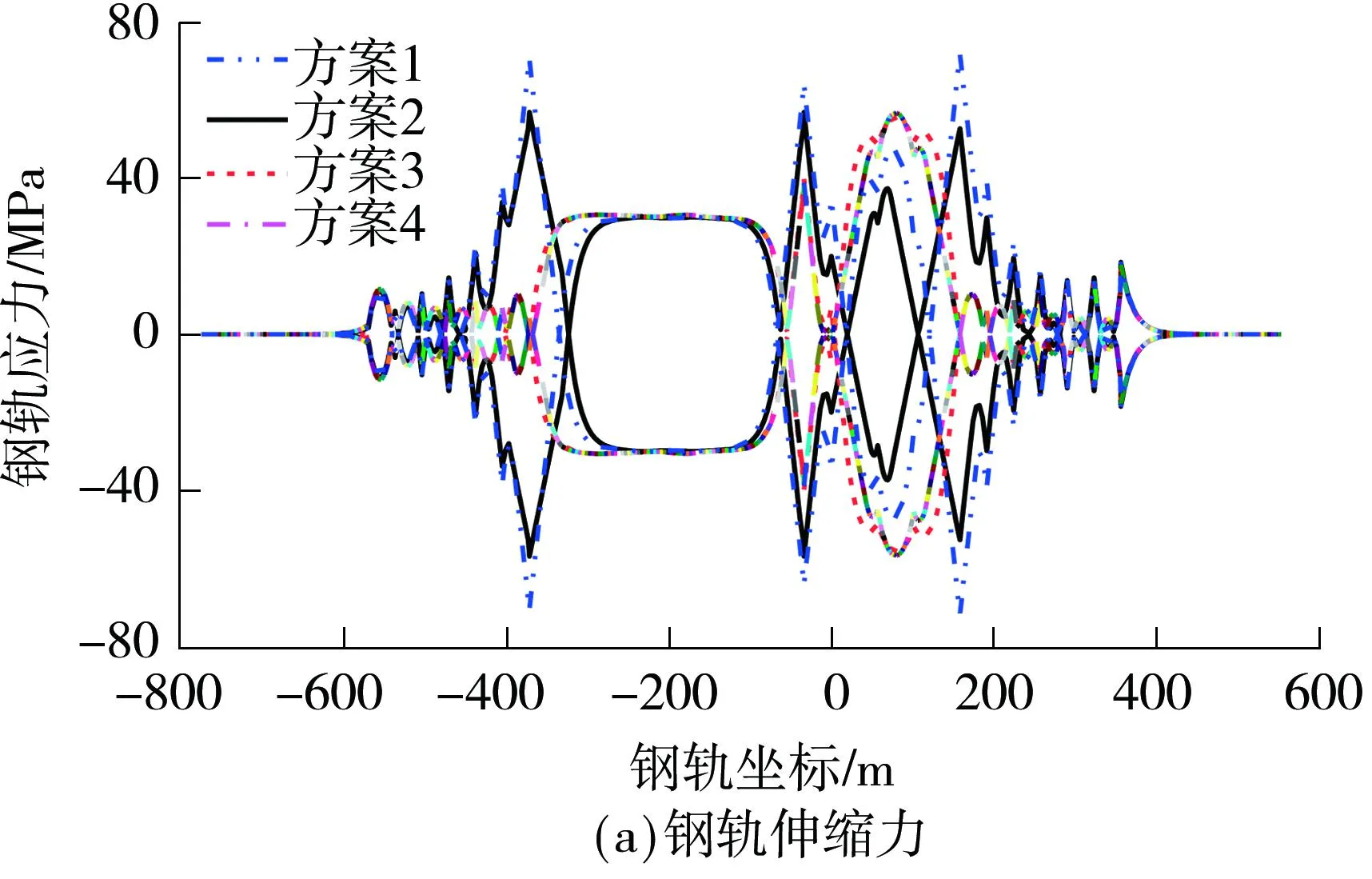
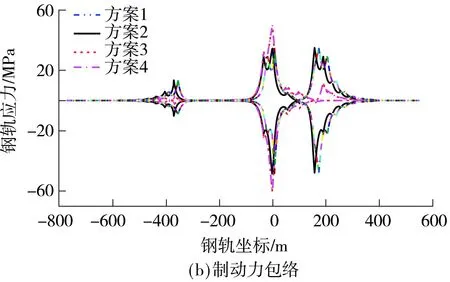
图11　钢轨纵向力包络对比

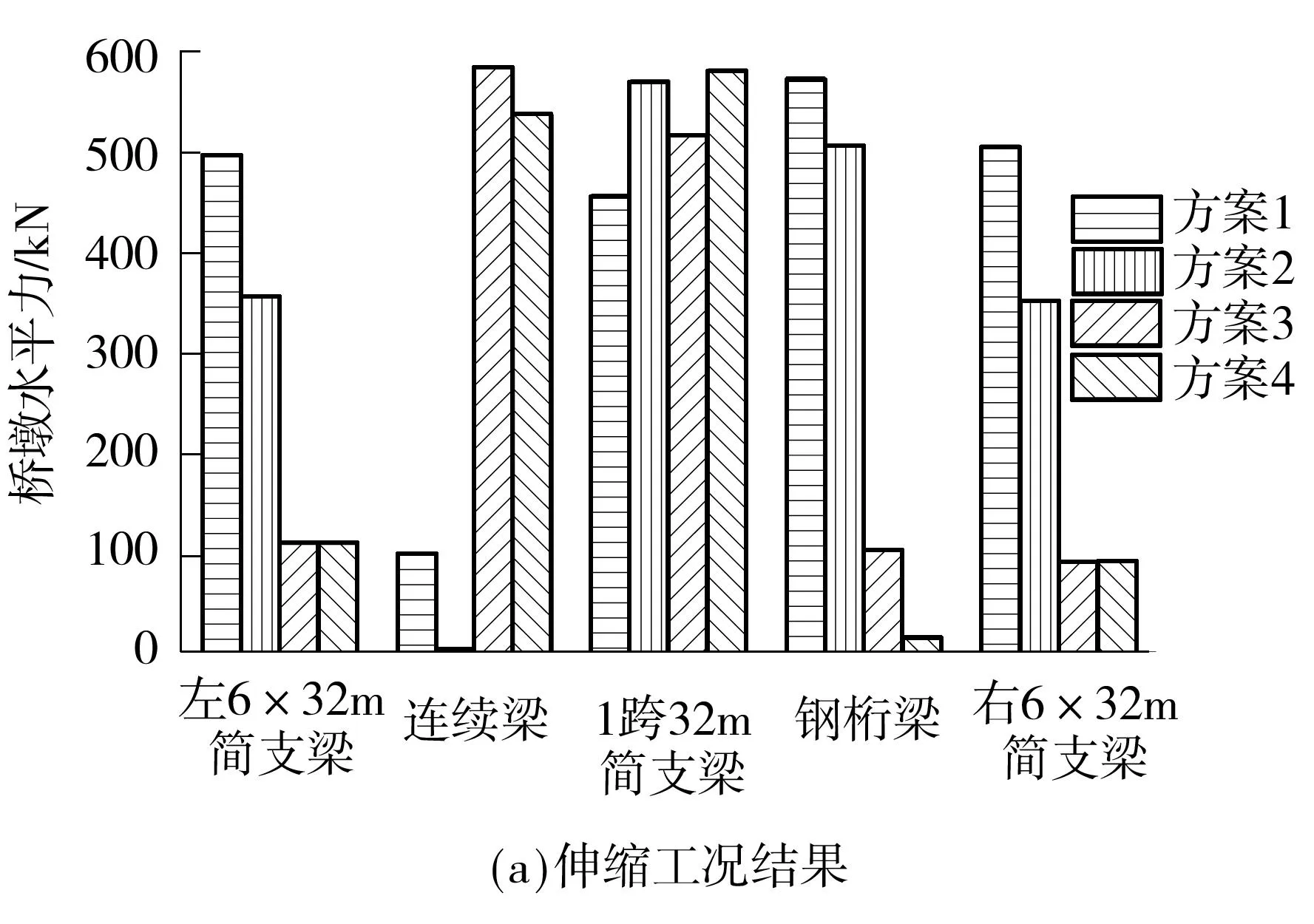
Fig.11　Comparison of the envelopes of rail force

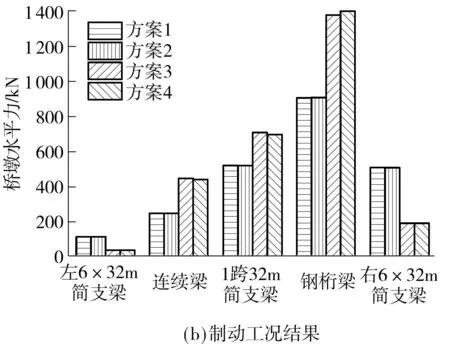
图12　顺桥向不同位置处墩顶水平力最大值对比

Fig.12Comparisonofthemaximumpierhorizontalforceatdifferentlocationsalongthebridge

由图12可知，伸缩工况下，设置小阻力扣件和钢轨伸缩调节器均可有效减小钢桁梁桥墩所受水平力，但会使相邻简支梁桥墩承受较大的水平力作用.制动工况下，设置小阻力扣件对各桥墩水平力的影响较小，设置钢轨伸缩调节器使连续梁、钢桁梁和两者之间的简支梁桥墩的水平力显著增大，两侧6×32m简支梁桥墩水平力显著减小.

在伸缩工况下，与方案3相比，方案4中钢轨伸缩调节器处的钢轨相对位移最多减小了10%，且发生在钢桁梁滑动支座端.

由于钢轨伸缩调节器是无缝线路中的薄弱环节，因此我国规范建议尽量减少钢轨伸缩调节器的使用[8].结合以上对比分析，当无缝线路检算不能满足规范要求时，可优先采用设置小阻力扣件来降低钢桁梁桥钢轨纵向力.当需要大幅降低钢轨应力时，可采用设置钢轨伸缩调节器并在其附近铺设一定范围小阻力扣件的无缝线路布置方案.

设置小阻力扣件时，需要进行钢轨断缝检算[8].本节假定钢轨降温45 ℃时在受力最大值位置(即钢桁梁滑动支座处)折断，同时考虑梁体降温，得到方案2中钢轨断缝值为84mm，小于文献[8]规定的困难条件下钢轨断缝容许值(90mm).

5　结论

文中采用有限元模型对钢桁梁桥主体桁架和桥面系结构进行了适当的简化，降低了建模难度，提高了计算效率，同时具有较好的准确性，主要结论包括：

(1)由于温度跨度大，加之钢材线膨胀系数相对较大，控制文中156m简支钢桁梁桥上无缝线路钢轨强度检算的钢轨伸缩拉应力达47.9MPa，稳定性检算时钢轨最大伸缩压应力达到了84.5MPa.

(2)若下部结构刚度相差较小，在分析大跨简支钢桁梁桥上无缝线路纵向力时，两侧的多跨简支梁可按6跨进行简化.

(3)相邻简支梁跨度对钢桁梁固定端钢轨伸缩力影响较大，与32m标准跨度相比，24m跨度时固定端伸缩力降低了9%，40m跨度时固定端伸缩力增大了7%.

(4)相邻大跨连续梁对钢桁梁固定端钢轨伸缩力影响显著，应予以考虑.在连续梁与钢桁梁之间布置1跨或2跨简支梁，可大幅降低相邻连续梁对钢桁梁固定端钢轨应力的不利影响.

(5)当无缝线路检算不能满足规范要求时，可优先采用设置小阻力扣件来降低钢桁梁桥的钢轨纵向力.当需要大幅降低钢轨应力时，可采用设置钢轨伸缩调节器并在其附近铺设一定范围小阻力扣件的无缝线路布置方案.

(6)设置小阻力扣件后，伸缩工况下钢桁梁钢轨应力最大值和桥墩水平力均显著减小，但需对钢轨断缝进行检算.本桥设置小阻力扣件后钢轨断缝值小于规范中规定的困难条件下钢轨断缝容许值.

[1]YANBin,DAIGonglian,HUNan.Recentdevelopmentofdesignandconstructionofshortspanhigh-speedrailwaybridgesinChina[J].EngineeringStructures,2015,100:707- 717.

[2]MATSUMOTON,ASANNUMAK.Someexperienceontrack-bridgeinteractioninJapan[M]∥CalcadaR.Track-bridgeInteractiononHigh-SpeedRailways.London:CRCPress/Balkema,2009:77- 94.

[3]卜一之.高速铁路桥梁纵向力传递机理研究 [D].成都：西南交通大学土木工程学院，1998.

[4]广钟岩，高慧安.铁路无缝线路 [M].北京：中国铁道出版社，2005:223- 332.

[5]DAIGonglian,SUMiao,YANBin.Casestudyoftwincable-stayedbridgesforhigh-speedrailwayinChinadesign,analysisandconstruction[J].StructuralEngineeringInternational,2014,24(3):396- 401.

[6]闫斌.高速铁路中小跨度桥梁与轨道相互作用研究 [D].长沙：中南大学土木工程学院，2013.

[7]闫斌,戴公连.考虑加载历史的高速铁路梁轨相互作用分析 [J].铁道学报,2014,36(6):75- 80.

YANBin,DAIGong-lian.Analysisofinteractionbetweencontinuouslyweldedrailandhigh-speedrailwaybridgeconsideringload-history[J].JournaloftheChinaRailwaySociety,2014,36(6):75- 80.

[8]TB10015—2012,铁路无缝线路设计规范 [S].

[9]DS899/59，铁路新干线上桥梁的特殊规程 [S].

[10]UIC774- 3，Track/bridgeinteractionrecommendationsforcalculations[S].

[11]于向东,沙嵩,闫斌.客货共线大跨度简支钢桁梁桥梁轨相互作用 [J].湖南大学学报,2014,41(6):106- 111.

YUXiang-dong,SHASong,YANBin.Track-bridgeinteractionoflong-spansimplysupportedsteeltrussbridgeinmixedpassengerandfreightrailway[J].JournalofHunanUniversityNaturalSciences,2014,41(6):106- 111.

[12]SONGMK,NOHHC,CHOICK.Anewthree-dimensionalfiniteelementanalysismodelofhigh-speedtrain-bridgeinteractions[J].EngineeringStructures,2003,25(13):1611- 1626.

[13]谢旭,王炎,陈列.轨道约束对铁路减隔震桥梁地震响应的影响 [J].铁道学报,2012,34(6):75- 82.

XIEXu,WANGYan,CHENLie.Effectofrailrestraintsonseismicresponseofcushioningrailwayrridges[J].JournaloftheChinaRailwaySociety,2012,34(6):75- 82.[14]DAIGong-lian,YANBin.Longitudinalforcesofcontinuouslyweldedrailonhigh-speedrailwaycable-stayedbridgeconsideringimpactofadjacentbridges[J].JournalofCentralSouthUniversity,2012,19(8):2348- 2353.

[15]孙数礼.高速铁路桥梁设计与实践 [M].北京：中国铁道出版社,2011:166- 193.

InfluenceofAdjacentBridgesonInteractionSystemofLarge-SpanSteelTrussGirderandRailway

YU Xiang-dong1YIN Xing-quan2YAN Bin1

(1.SchoolofCivilEngineering,CentralSouthUniversity,Changsha410075,Hunan,China; 2.BridgeEngineeringDesignandResearchInstitute,ChinaEngineeringConsultingGroupCo.,Ltd.,Beijing100055,China)

Bytakinga156mlarge-spansimply-supportedsteeltrussgirderontheHuangling-Hancheng-Houmalineasacase,theinfluenceofadjacentbridgesonthelongitudinalforcedistributioninthecontinuously-weldedrail(CWR)onthesteeltrussgirderisanalyzed,andsomesuggestionsarepresentedfortheselectionofrelevantparameters.Intheinvestigation,nonlinearspringisusedtosimulatethelongitudinalresistanceofCWRandthebeamelementwithrigidarmsisemployedtosimulatethesteeltrussbridge.Calculationresultsshowthat(1)whenthelongitudinalstiffnessofthesubstructurehasnoobviousvariation,themulti-spansimply-supportedbeamsatbothsidesofthesteeltrussgirdercanbesimplifiedintoagirderwith6spansforanalyzingthelongitudinalforce; (2)ascomparedwiththestandardspanof32mforsimply-supportedbeams,aspanof24mmayresultinaforcedecreaseatthefixedendby9%,whileaspanof40mmayresultinaforceincreaseby7%; (3)bytakingtheadjacentlarge-spancontinuousbeamintoconsideration,thelongitudinalforceatthefixedendofthesteeltrussgirderincreasesby2.2timesandthemaximumcompressivestressofthefullbridgeincreasesby12%; (4)thelongitudinalforceatthefixedendofthesteeltrussgirderissignificantlyreducedwhensimply-supportedbeamswithoneortwospansarearrangedbetweenthecontinuousbeamandthesteeltrussgirder;and(5)fastenerswithsmallresis-tancehelpstoreducethemaximumstressandthehorizontalforceloadedonthepier.

railwaybridge;railwayengineering;long-spansteeltrussgirder;adjacentbridge;small-resistancefastener

于向东(1970-)，男，博士，副教授，主要从事桥梁抗风及梁轨相互作用研究.E-mail:xdyu@csu.edu.cn

† 闫斌(1984-)，男，博士后，讲师，主要从事铁路桥梁-轨道相互作用研究.E-mail：binyan@csu.edu.cn

1000- 565X(2016)06- 0137- 06

U213.9

10.3969/j.issn.1000-565X.2016.06.021