汽车横向稳定杆的参数化分析及优化*

石柏军　刘德辉　李真炎

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)



汽车横向稳定杆的参数化分析及优化*

石柏军刘德辉李真炎

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

对汽车横向稳定杆的几何尺寸进行参数化处理,采用莫尔积分法推导横向稳定杆的侧倾角刚度计算公式并初步校核强度，通过有限元仿真分析验证该方法的可行性；针对某SUV，以侧倾角刚度为优化目标，采用比例系数优化法对该车的横向稳定杆进行优化设计；然后在ADAMS/Car中建立整车动力学仿真模型，以转向盘角阶跃实验验证优化的效果，最后进行整车实验验证.仿真和实验结果表明，侧倾角刚度较大的横向稳定杆更有助于提高汽车的侧倾稳定性，这进一步验证了文中优化设计的可行性.

车辆工程；横向稳定杆；优化设计；参数化；侧倾角刚度；侧倾稳定性

当汽车发生侧倾时，两侧悬架之间的相对反向跳动使横向稳定杆受到扭矩的作用，但因受其杆身的扭转刚度的影响，弹性的稳定杆所产生的扭转的内力矩妨碍了悬架弹簧的变形，从而减少了车身的侧倾.国内现有的横向稳定杆参数化设计方法能利用CAD参数化建模功能实现三维模型的自动生成，提高了横向稳定杆的开发效率[1].国外学者曾提出一种主动横向稳定杆，它能根据不同路面情况调节适合的稳定杆刚度，使车辆能兼顾行驶舒适性和操纵稳定性[2].文中通过对横向稳定杆的参数化分析，采用比例系数法对其进行优化，最后在软件仿真和实车实验中证明优化后的横向稳定杆能使整车具有更好的侧倾稳定性.

1　横向稳定杆的参数化分析

1.1几何尺寸参数化

横向稳定杆是悬架系统的附属部件，其结构形状会根据车辆的不同而变化，从而呈现外观和形状的多样化.尽管每辆汽车的横向稳定杆的大小和形状都不一样，但其外形大体上呈“U”型结构.为了研究方便，可把横向稳定杆的形状作一定的简化处理：忽略横向稳定杆截面形状的变化，把其看作截面为等圆的杆；此外，忽略各种不规则的圆弧过渡，忽略稳定杆与车身相连接的橡胶衬套的变形，认为横向稳定杆整体在同一平面内[3].由于车身的侧倾角度通常很小(在0°～5°范围内)，因此把稳定杆端部的变形看作小变形.综合上述各种假设，可以用几个简单的参数描述横向稳定杆的几何尺寸，从而实现对横向稳定杆的参数化分析.简化后的横向稳定杆模型如图1所示.图1中，C、D点为横向稳定杆与车身或者车架的铰接点，B、H点为稳定杆杆身末端点，A、J点为横向稳定杆杆臂端点.L1为横向稳定杆杆身长度，L2为横向稳定杆与车身或者车架铰接点之间的距离，L为横向稳定杆杆臂长度，θ为横向稳定杆的杆身与杆臂之间的夹角，假定稳定杆的直径为d，通过以上5个参数描述即可确定稳定杆的几何形状，同时可把其几何尺寸进行参数化处理.

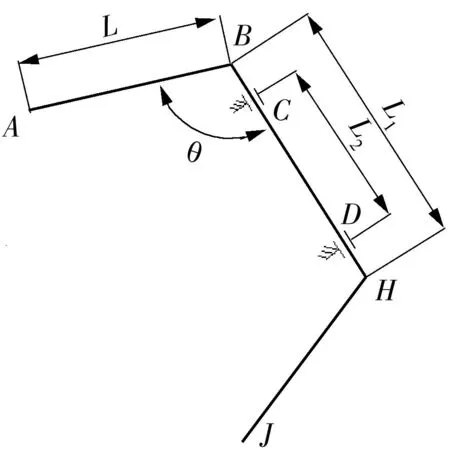
图1　简化后的横向稳定杆模型

1.2侧倾角刚度计算

对横向稳定杆进行参数化处理后，便可根据这些参数计算横向稳定杆的侧倾角刚度.横向稳定杆所受载荷为反对称性载荷，据此可知横向稳定杆对称中心的扭转角度为0°，其竖直方向的位移也为0[4].C、D点由于橡胶套筒的约束允许横向稳定杆在这两个位置只能绕着轴线转动和沿着轴线运动.为了计算横向稳定杆的侧倾角刚度，需要先计算A、J点在反对称力F作用下的位移.

下面采用莫尔积分法[5- 6]计算横向稳定杆在反对称力F作用下A点的位移.由于横向稳定杆的几何形状呈对称性，受力呈反对称性，因此取其一半进行受力分析即可.假定横向稳定杆的对称点为O点，将该点看作固定端点，根据莫尔积分法原理，分别对稳定杆端点A在力F和单位力作用下进行受力分析.莫尔积分法受力分析如图2所示.

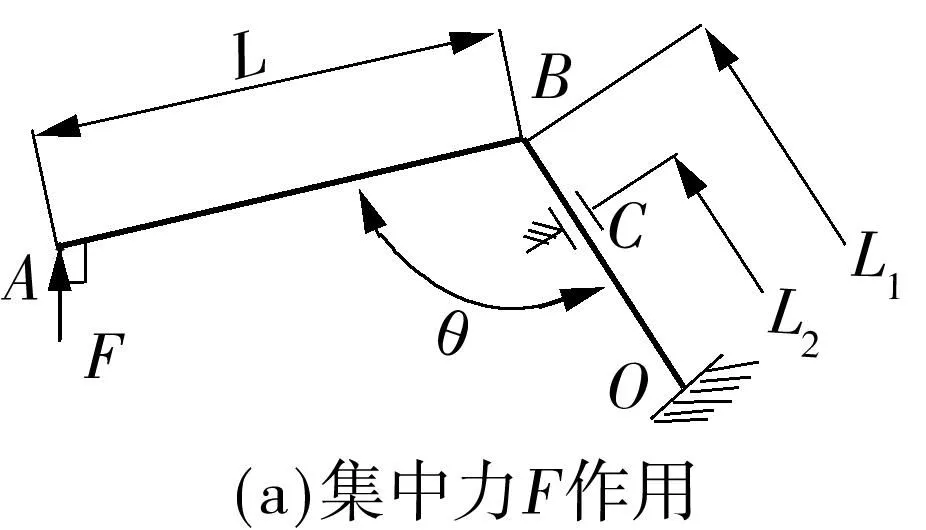
图2　莫尔积分法受力分析

横向稳定杆的端点在力F作用下时，AB段受到弯矩作用而变形，BC段受到弯矩、扭矩组合作用变形，CO段也受到弯矩、扭矩组合作用变形.根据受力分析对图2中的AB段分别列出其距端点A的弯矩变量，对BC段也分别列出其距对称中心点O的弯矩与扭矩变量，见表1.

根据受力分析，忽略橡胶衬套的变形，忽略CO段在弯矩作用下的微小角位移对BC段造成的位移的影响，设A点的位移为ΔA，E为材料弹性模量，Iz为横向稳定杆截面主惯性矩，G为材料切变模量，Ip为横向稳定杆截面极惯性矩，υ为材料的泊松比，由莫尔积分法可得

表1　受力情况变量表

(1)

根据材料力学有G=E/[2(1+υ)]，Ip=2Iz，对式(1)进行积分可得

(2)

其中，Δ1=L1-L2.

A点相对于横向稳定杆杆身的角位移φ为

(3)

A点相对于横向稳定杆杆身的恢复力偶距M为

M=F(L1-2Lcosθ)

(4)

设Kφ为横向稳定杆的侧倾角刚度，联立式(1)-(4)并考虑横向稳定杆工作时为微变形，可得横向稳定杆的侧倾角刚度为

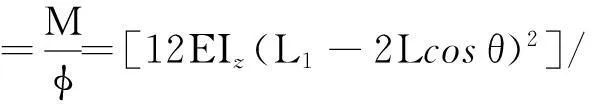
(5)

由式(5)可以看到，只要知道横向稳定杆的几何尺寸参数并确定材料特性，便可计算出其侧倾角刚度.在侧倾角刚度作为汽车选用横向稳定杆的重要考虑因素下，此公式为横向稳定杆的初步选择提供了重要的参考依据.

1.3强度校核

根据侧倾角刚度初步选好横向稳定杆后，需要对其强度进行校核，以检验其是否达到使用的要求.如果横向稳定杆的强度达不到要求，那么汽车在严峻的行驶工况下极易造成横向稳定杆的破裂损坏，从而可能导致交通事故的发生[7].要对横向稳定杆进行强度校核，需要确定横向稳定杆工作时受到相当应力最大的截面.当其应力超过横向稳定杆的承受范围时，横向稳定杆通常从这些危险截面开始破裂直至损坏，从而使横向稳定杆丧失工作能力.由式(2)和图1可求出横向稳定杆所受的支撑反力，然后画出横向稳定杆的弯矩和扭矩图，如图3所示.

图3　横向稳定杆的弯矩与扭矩图

Fig.3Bendingandtorquemomentdiagramsoftheanti-rollbar

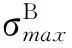
(6)

式中，Wz为杆臂的弯曲截面系数.

(7)

(8)

其中，Wp为杆身的扭转截面系数.

(9)

(10)

(11)

把式(5)代入式(2)，可得

(12)

若得到汽车悬架弹簧的最大行程或横向稳定杆工作时横向稳定杆杆臂的最大位移以及横向稳定杆材料的设计许用应力，即可根据式(9)-(12)对横向稳定杆工作时的强度进行初步校核，以判断横向稳定杆的设计是否合理.

1.4有限元仿真

下面将对横向稳定杆进行有限元仿真分析，以验证横向稳定杆的侧倾角刚度的计算和危险截面判断的正确性.有限元仿真分析中的横向稳定杆的几何尺寸采用某SUV现有的横向稳定杆(文中将其称为B型横向稳定杆)的几何尺寸.为了仿真分析的简便性，对该杆进行适当的简化处理，将横向稳定杆看作等截面圆，有限元仿真模型中加入杆身与杆臂之间半径为R的倒圆角，以使仿真模型和实物模型更加接近.仿真模型中的横向稳定杆的具体几何参数如下：L为278mm，L1为760mm，L2为640mm，θ为127.7°，d为30mm，R为40mm.

根据横向稳定杆的具体几何参数，在Catia软件建立横向稳定杆的空间几何模型，如图4所示.然后把三维模型导入Hypermesh中进行网格划分.网格采用三维十节点四面体结构solid92单元，该单元能模拟不规则网格且具备计算大变形和大应变的能力[8]，适合模拟横向稳定杆大变形大应变的实际情况.模型共划分为15 380个单元、132 059个节点.网格划分好后，便可以创建接触对，即橡胶衬套和横向稳定杆之间的接触，这里为面-面接触，并且为线性接触，同时忽略接触间的摩擦[9].

图4　Catia中建立的横向稳定杆几何模型

在有限元仿真分析中，横向稳定杆的材料选用50CrVA，弹性模量E为210GPa，泊松比υ为0.3，密度为7.85g/cm3.把套筒当作刚体，对套筒外表面施加沿各个方向的固定位移约束，对稳定杆端部截面圆中心施加方向相反、大小为2 500N的集中载荷，方向垂直于横向稳定杆整体所在的平面.利用Radioss对横向稳定杆进行有限元计算，所得有限元仿真分析结果如图5所示.

图5　B型横向稳定杆位移与应力云图

Fig.5DisplacementandstresscontoursoftheB-typeanti-rollbar

由仿真结果可知:横向稳定杆的最大位移发生在杆臂的末端，最大变形位移为9.674mm；最大应力发生在横向稳定杆与套筒的连接面上，最大vonMises应力为308.0MPa.根据横向稳定杆的具体几何参数，利用前面所述的分析方法计算该杆的理论最大变形位移和最大应力，并和仿真分析结果进行对比，结果如表2所示.

表2横向稳定杆的理论计算与仿真分析结果对比

Table2Comparisonofresultsbetweentheoreticalcalculationandsimulationoftheanti-rollbar

方法最大位移/mm最大位移点最大应力/MPa最大应力点理论计算10.024杆端部300.16C截面上端有限元计算9.674杆端部308.00C截面上端误差/%-2.62.55

由表2可知，横向稳定杆的理论计算与仿真分析误差在5%以内，考虑到模型的简化和网格密度等的影响，在小误差范围内，仿真结果和理论计算结果吻合得较好，仿真分析中所体现出来的最大位移点和最大应力点也与理论计算的情况相吻合，证明此参数化分析方法是有效的.

2　横向稳定杆的优化设计

根据几何尺寸参数化后的横向稳定杆可知，要使横向稳定杆能在已确定结构的汽车上正确安装，Lsinθ、L1-2Lcosθ的值应为确定的常数.根据这个原则对该SUV的横向稳定杆进行优化设计[10- 11].根据图1和1.4节中B型横向稳定杆的几何参数进行计算，可知要使横向稳定杆能在SUV车型上正确安装，应满足

Lsinθ=0.22

(13)

L1-2Lcosθ=1.1

(14)

文中假定横向稳定杆的直径d为30mm，在保持其直径和安装条件不变的情况下，通过优化其他参数来提高横向稳定杆的侧倾角刚度.把式(13)、(14)都表示成θ的函数，并假定L2与L1的比值为N，将这些关系式代入式(5)，通过简单的计算并化简可得到

Kφ=121 238.576 5sin3θ/

{0.085 2+Psin3θ[0.755+P2Q31.32PQ2cotθ+0.580 8Qcot2θ]}

(15)

其中：P=1.1+0.44cotθ;Q=1-N,N为比例系数.

式(15)中的横向稳定杆的侧倾角刚度是关于θ和N的函数关系式，根据实际情况，易知N的取值范围在0和1之间.汽车的车身宽度一般在1.5m以内，以1.5m为横向稳定杆杆身长度L1的最大值，横向稳定杆与车身的两个铰接点之间的最小距离L2为0m，根据这些极限范围很容易得到θ的取值在30°～160°之间.以θ为横坐标，Kφ为纵坐标，根据式(15)，N分别取0～1之间且间隔为0.1的11个数，在Matlab中分别作出这些关系曲线，如图6所示.

由图6可知，在N非常小的情况下(N=0.0或0.1),横向稳定杆的侧倾角刚度随着夹角θ的增加而增加，此时横向稳定杆的杆身与车身的两个铰接点之间的距离非常小.虽然这时增大夹角能增加横向稳定杆的侧倾角刚度，但增大的程度有限，且容易造成材料的耗费.当N增大时，横向稳定杆的侧倾角刚度随着横向稳定杆杆身与杆臂的夹角的增加呈先增加后减少的趋势，横向稳定杆的侧倾角刚度的最大值出现在2～2.5rad之间，且随着N值的增大横向稳定杆的侧倾角刚度的最大值会稍微增大，最大值出现在更加接近2.5rad夹角的时候.此比例系数优化法为进行不同车型横向稳定杆的优化设计提供了指导.对于该SUV在设计横向稳定杆时，在满足安装条件的前提下，可以尽量选择更大的比例系数N，且使横向稳定杆杆身与杆臂的夹角在2～2.5rad之间，这样就可以用较少的材料获得较大的侧倾角刚度值.

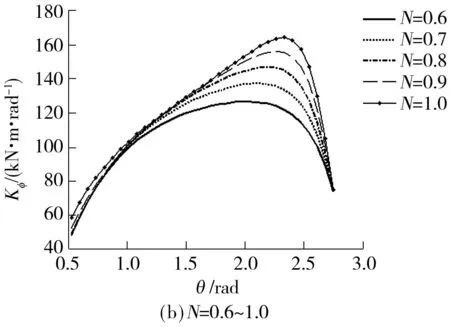
图6　不同比例系数下横向稳定杆侧倾角刚度的变化曲线

Fig.6Curvesofrollstiffnessoftheanti-rollbarsunderdiffe-rentproportionalitycoefficients

在对横向稳定杆进行优化设计时，需要考虑其能否满足使用的强度条件.将上述优化设计过程的约束参数代入式(10)，可得

(16)

由式(16)可以看到，在已确定结构的汽车上，当横向稳定杆所受到的载荷确定时，横向稳定杆所受到的最大应力只与横向稳定杆杆身与车身的铰接点之间的距离L2有关.因此，从横向稳定杆的结构和寿命上考虑，当所选择的L2值与横向稳定杆的两个端点之间的水平距离越接近时，横向稳定杆所受到的最大应力就越小.在此原则指导下进行优化设计时，除了要考虑上述优化设计的规律外，还应使L2的值尽量接近横向稳定杆杆臂两端点之间的水平距离，以减少横向稳定杆工作时所受到的最大应力值，从而增加横向稳定杆的使用寿命.

3　软件仿真与整车实验对比

3.1ADAMS/Car工况仿真

由于该SUV车型的B型横向稳定杆的几何参数已达到较优化，为了进行对比，将引入图6中N=0.4、θ=2rad时的横向稳定杆(A型横向稳定杆)进行建模，以在ADMAS/Car软件中进行仿真实验[12]，其参数如下：L为242m，L1为898.5mm，L2为359.4mm，θ为114.6°，d为30mm，R为40mm.

本次进行的仿真分析实验主要是转向盘角阶跃实验[13- 14]，这个实验能反映车辆自身的侧倾稳定性能，从而判断不同横向稳定杆的抗侧倾效果的优劣.仿真车辆分别配备了上述的A型与B型横向稳定杆，以下简称A型车辆和B型车辆.

转向盘角阶跃实验流程如下：根据该SUV的整车参数，通过计算并取整可得到实验车辆的车速为100km/h，根据国标要求，为了使实验车辆稳态后的侧向加速度达到0.5 g左右，应该在0.3s内使实验车辆的方向盘转过45°[15].仿真结束后所得横摆角速度响应曲线、横向加速度响应曲线和侧倾角随横向加速度变化的关系如图7所示.

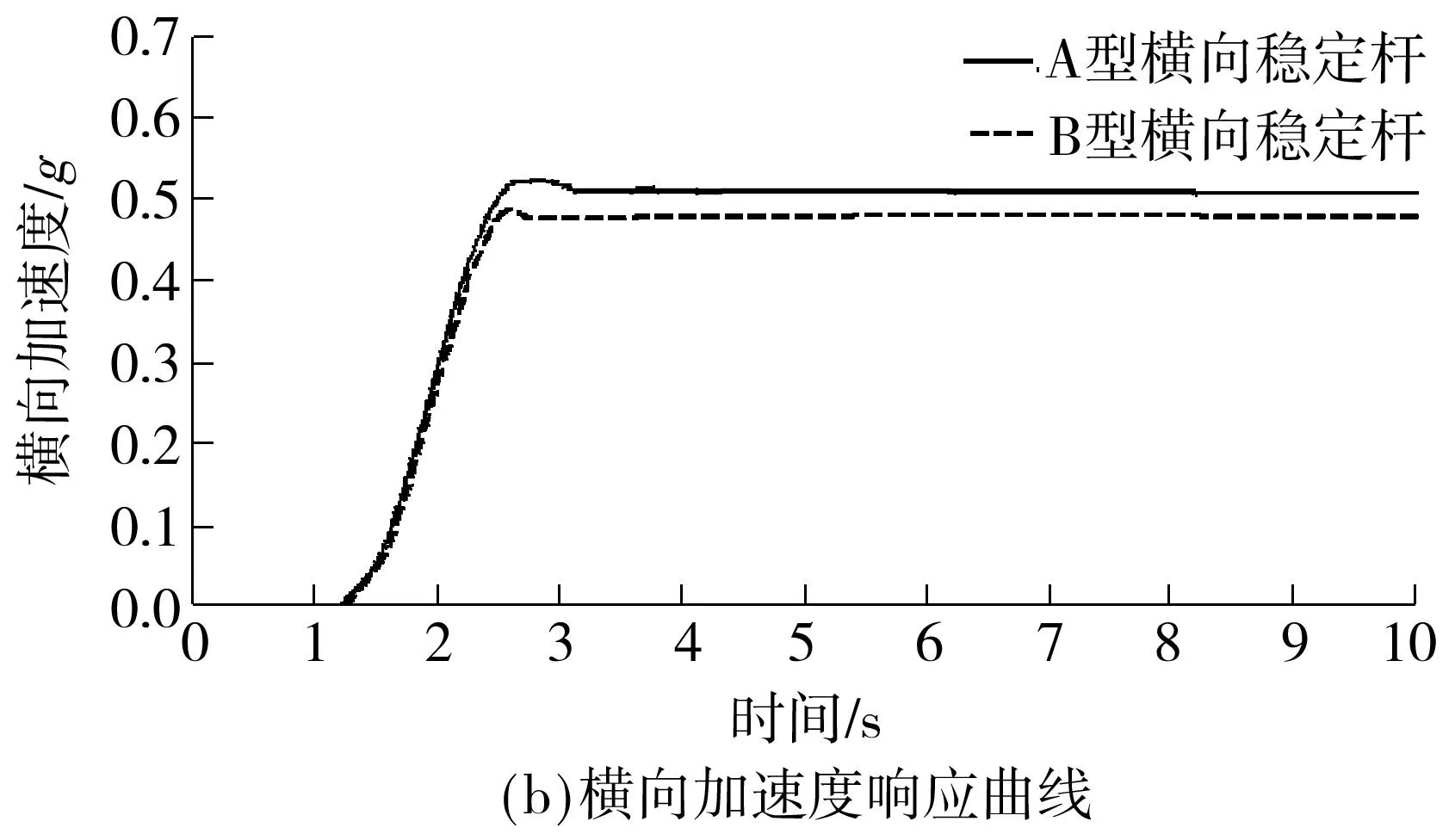
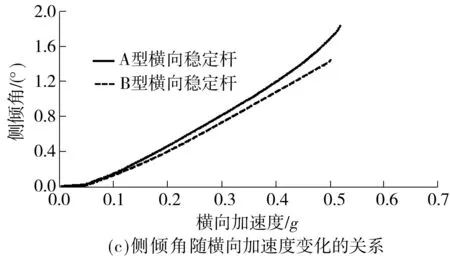
图7　转向盘角阶跃工况仿真曲线

Fig.7Simulationcurvesunderthesteeringwheelstepinputtest

从图7(a)可知，在仿真实验过程中B型车辆比A型车辆进入稳态响应的时间稍提前一点.由图7(b)可知，A型车辆的稳态横向加速度超过了0.5g，而B型车辆的稳态横向加速度只有0.48g，因此B型车辆具有更高的侧倾稳定性.由图7(c)可知，车辆的侧倾角与横向加速度大致呈线性增长关系，这与理论计算相符合，由于A型车辆横向稳定杆的侧倾角刚度比B型车辆的要小，因此随着横向加速度的增大，A型车辆的侧倾角度要比B型车辆的大，且两车之间的侧倾角差值增大.

3.2整车实验

实验车辆和场地由某公司提供，实验所选用的B型横向稳定杆为该车辆原有的横向稳定杆，实验选用的A型横向稳定杆根据3.1节中A型横向稳定杆的参数设计加工而成.实验前应对实验车辆的功能和使用状况进行检查，以保证车辆各方面功能良好，实验道路应满足转向盘角阶跃实验中国家规定的标准.实验过程中的数据采集系统采用实验室自主开发的集数据采集与显示功能一体化的数据采集处理系统(简称为AccRoll系统)，该系统能利用陀螺仪采集得到车辆的横摆角速度、横向加速度和侧倾角等数据[16- 17].装有横向稳定杆的实验车辆如图8所示.

图8　装有横向稳定杆的实验车辆

3.2.1A型横向稳定杆

对A型车辆进行方向盘角阶跃实验，所得的侧倾角、横向加速度响应曲线和侧倾角随横向加速度变化的关系如图9所示.

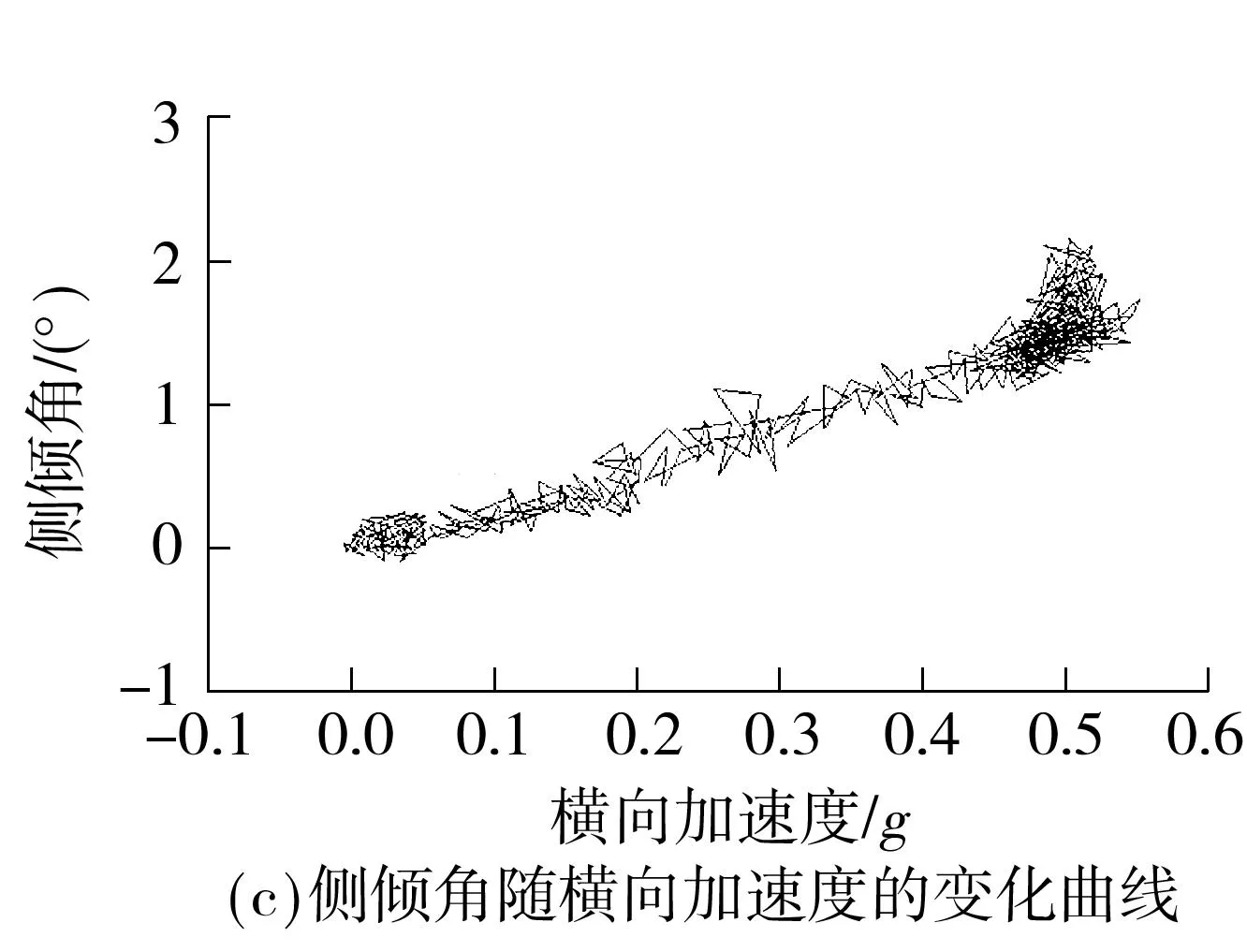
图9　A型横向稳定杆转向盘角阶跃实验曲线

Fig.9CurvesofsteeringwheelstepinputtestonA-typeanti-rollbar

对比图7(b)和图9(b)、图7(c)和图9(c)可知，在仿真实验中，稳态响应后，A型车辆的横向加速度和侧倾角分别为0.51g和1.78°，而实验结果的平均值分别为0.52 g和1.61°，误差分别为2.0%和-9.6%，考虑到简化和其他原因带来的误差，在一定的误差允许范围内，实验和仿真结果吻合得较好.

3.2.2B型横向稳定杆

对B型横向稳定杆车辆进行方向盘角阶跃实验，所得的侧倾角、横向加速度响应曲线和侧倾角随横向加速度变化的关系如图10所示.

图10　B型横向稳定杆转向盘角阶跃实验曲线

Fig.10CurvesofsteeringwheelstepinputtestonB-typeanti-rollbar

对比图7(b)和图10(b)、图7(c)和图10(c)可知，在仿真实验中，稳态响应后，B型车辆的横向加速度和侧倾角分别为0.48 g和1.49°，而实验结果的平均值分别为0.47 g和1.42°，误差分别为2.1%和-4.7%，仿真和实验结果吻合较好.

从仿真与整车实验结果的对比可知，在较小的误差范围内，实验和仿真结果整体上吻合得较好，这说明通过仿真对实验进行预测是可行和准确的.通过以上对比可知，B型横向稳定杆的侧倾稳定性更优.

4　结论

文中提出了一种针对横向稳定杆的参数化分析方法，该方法能简单、有效地推算出其侧倾角刚度，并进行强度校核.对于某SUV车型的横向稳定杆，通过对其受载荷时最大位移和最大应力的理论计算与有限元计算之间的对比，发现计算结果的误差均在可以接受的范围内，因此证明此分析方法是可行的.在此基础上，以侧倾角刚度为优化目标，采用比例系数优化法对横向稳定杆进行了优化.最后，通过在Adams/Car里的整车仿真和道路实车实验的对比，在转向盘角阶跃实验下，验证了优化后的横向稳定杆具有更好的侧倾稳定性.

[1]王靖岳,欧阳纯,梁洪明.汽车悬架横向稳定杆的参数化设计 [J].汽车工程师,2014(9):39- 41.

WANGJing-yue,OUYANGChun,LIANGHong-ming.Theparameterizeddesignofsuspensionanti-rollbarofthevehicle[J].AutoEngineer,2014(9):39- 41.

[2]CRONJEPH,ELSPS.Improvingoff-roadvehiclehandlingusinganactiveanti-rollbar[J].JournalofTerramechanics,2010(47):179- 189.

[3]李群,何耀华.基于CATIA的汽车横向稳定杆的参数化设计 [J].汽车工程师,2011(6):24- 26.

LIQun,HEYao-hua.Theparameterizeddesignofautomotiveanti-rollbarbasedonCATIA[J].AutoEngineer,2011(6):24- 26.

[4]曾迥立.悬架稳定杆刚度的计算与分析 [J].汽车科技,2004,9(5):14- 16.

ZENGJiong-li.Calculationandanalysisofsuspensionstabilizerrigidity[J].AutomotiveTechnology,2004,9(5):14- 16.

[5]黄小清,陆丽芳,何庭蕙.材料力学 [M].广州:华南理工大学出版社,2006.

[6]XINGYM,KISHIMOTOS,ZHAOYR.AnelectronmoiremethodforacommonSEM[J].ActaMechanicaSinica,2006(22):595- 602.

[7]王谊,张晓蓉,蒋西明.汽车侧向稳定性校核及稳定杆强度校核 [J].重庆工学院学报,2000,14(5):30- 32.

WANGYi,ZHANGXiao-rong,JIANGXi-ming.Thecalibrationoflateralstabilityandstabilizerbarstrengthofautomobiles[J].JournalofChongqingInstituteofTechnology,2000,14(5):30- 32.

[8]张瑞发,郑核桩,宋玮,等.汽车稳定杆的三维有限元分析 [C]∥崔京浩.第十二届全国结构工程学术会议论文集第Ⅰ册.重庆:清华大学出版社,2003:412- 415.

[9]宋健,邢如飞.带橡胶套的稳定杆有限元分析 [J].汽车工程,2005,27(5):592- 594.

SONGJian,XINGRu-fei.Finiteelementanalysisonstabilizer-barwithrubberbush[J].AutomotiveEnginee-ring,2005,27(5):592- 594.

[10]郑严.基于智能算法的结构可靠性分析及优化设计研究 [D].成都:西南交通大学机械工程学院,2012.

[11]YANGZhou,ZHANGYi-min,HUANGXian-zhen,etal.Reliability-basedrobustoptimizationdesignofautomobilecomponentswithnon-normaldistributionparameters[J].ChineseJournalofMechanicalEngineering,2013,26(4):823- 829.

[12]孙维汉,顾宏斌.基于ADAMS/Car汽车动力学仿真 [J].计算机应用,2004(6):19- 21.

SUNWei-han,GUHong-bin.ThesimulationofvehicledynamicbasedonADAMS/Car[J].ComputerApplication,2004(6):19- 21.

[13]饶剑.基于ADAMS的悬架系统动力学仿真分析与优化设计 [D].武汉:武汉理工大学汽车工程学院,2005.

[14]GB/T6323.3—94,汽车操纵稳定性实验方法,转向瞬态响应试验(转向盘角阶跃输入) [S].

[15]GIMG,NIKRAVESHP.Ananalyticalmodelofpneumatictyresforvehicledynamicsimulations(Part1):pureslips[J].InternationalJournalofVehicleDesign,1990,1(6):201- 205.

[16]孟武胜，朱剑波，黄鸿，等.基于LabVIEW数据采集系统的设计 [J].电子测量技术，2008，31(11):63- 65.

MENGWu-sheng,ZHUJian-bo,HUANGHong,etal.DataacquisitionsystembasedonLabVIEW[J].ElectronicMeasurementTechnology,2008,31(11):63- 65.

[17]ZHOUKai,WANGXu-dong,LIUJian.Real-timedataacquisitionsystemforvehicleABSteststand[J].InternationalJournalofVehicleSafety,2011,5(3):101- 107.

SupportedbytheNationalNaturalScienceFoundationofChina(51375168)

ParameterizedAnalysisandOptimizationofVehicleAnti-RollBar

SHI Bai-junLIU De-huiLI Zhen-yan

(SchoolofMechanicalandAutomotiveEngineering,SouthChinaUniversityofTechnology,Guangzhou510640,Guangdong,China)

Inthispaper,first,ageometryparameterizationoftheanti-rollbarisperformed.Next,theformulasoftherollinganglestiffnessarededucedbymeansoftheMooreintegralmethod,followedbyapreliminarystrengthverification.Then,afiniteelementsimulationiscarriedouttoverifythefeasibilityoftheproposedmethod.Moreover,anoptimizationdesignoftheanti-rollbarofaSUVisconductedviatheproportionalitycoefficientmethod,withtherollinganglestiffnessastheoptimizationobjective.Finally,asimulationmodelisestablishedinADAMS/Cartoverifytheeffectivenessoftheoptimizationthroughasteeringwheelstepinputtest,followedbyarealcarexperiment.Theresultsofboththesimulationandtherealcarexperimentshowthatgoodrollstabilitycanbeobtainedatahighrollinganglestiffnessoftheanti-rollbar.Itisthusconcludedthattheproposedoptimizationmethodisfeasible.

automotiveengineering;anti-rollbar;optimizationdesign;parameterization;rollinganglestiffness;rollstability

2015- 06- 01

国家自然科学基金资助项目(51375168)

石柏军(1966-)，男，博士，副教授，主要从事车辆车身连接技术研究.E-mail:bjshi@scut.edu.cn

1000- 565X(2016)06- 0098- 07

U270.2

10.3969/j.issn.1000-565X.2016.06.016