三角形解的个数的进一步讨论
2016-08-08刘振龙福建省泉州培元中学
刘振龙(福建省泉州培元中学)
三角形解的个数的进一步讨论
刘振龙
(福建省泉州培元中学)
在学习了正弦定理、余弦定理之后,学生经常对如何判断三角形解的个数而烦扰。结合初中全等三角形的判定定理,若已知三角形的三边(且符合任意两边之和大于第三边)、两边一夹角、两角一边,则该三角形有唯一解。但是如果已知三角形的两边及其中一边的对角时,解的情况又如何呢?普通高中课程标准实验教科书《数学必修5》在第8页到第9页的“探究与发现《解三角形的进一步讨论》”中有详细的说明(此处略),但分类种数较多,学生容易混淆结论,故在实际操作中仍存在很多困惑。因此,针对学生的具体学情,笔者以课堂实例为依托,对已知“两边一对角”的三角形解的个数问题进行多种方法的探究讨论。
【例1】在△ABC中,若a=18,b=24,A=45°则此三角形解的个数为______。
综上,该三角形有两解。
方法二:画圆找交点
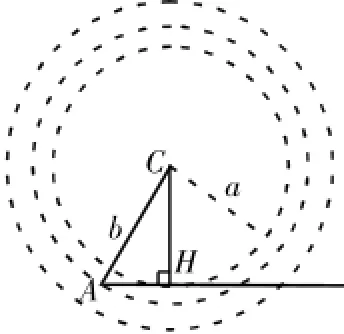
解:由于角A为已知角,故先画出角A,在角A的其中一边上确定顶点C,使得AC=24,即b=24,接着以点C为圆心,a=18为半径画圆,观察所画得的圆与角A的另一边出现的交点个数(交点即为三角形的顶点B),若没有交点,则说明该三角形无解;若只有一个交点,则说明该三角形解的个数为1个;若有两个交点,则说明该三角形解的个数为2个。
如图所示,以C为圆心,为半径所画得的圆与角A的另一边交于B1,B2两点,故该三角形有两解。在判断交点个数时,可利用半径a与过点C作射线AB1的垂线段CH的长度大小进行对比:若a<CH,则无交点;若a=CH,则有一个交点;若CH<a<b,则有两个交点;若a≥b,则有一个交点。

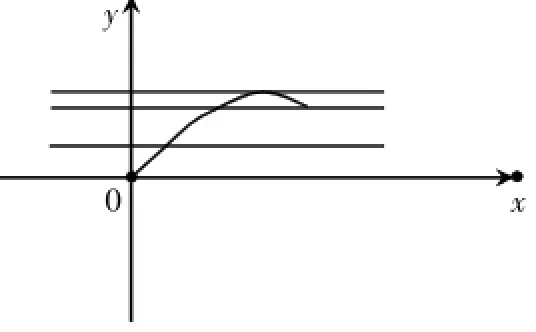
方法一:正弦定理
方法二:画圆找交点
方法三:二次方程的正根个数
已知两边一角问题,也可对角A应用余弦定理,并将其整理成关于边长c的一元二次方程c2-2bcosA·c+b2-a2=0,若该方程无实根或只有负数根,则该三角形无解;若方程有一个正数根,则该三角形有一解;若方程有两个不相等的正数根,则该三角形有两解。
对于例2,若应用“方法三”,可以得到关于边长c的一元二次方程c2-bc+b2-3=0。由题意,要使得该方程有一个正数根,结合二次函数的图象特点(对称轴为),可得Δ=(-b)2=4(b2-3)=0或者b2-3≤0,解得b=2或。
数学教学活动中,不断渗透、总结相关的数学思想并有效地理解掌握,对于寻找解题途径和提高解题能力具有重大意义。上述方法体现了数学学习中常见的分类讨论思想、数形结合思想、化归思想等多种数学思想。当面临问题时,先思考该问题所属类别,尽可能多地联想解决此类问题所能包含的各种数学思想,选择其中一种或多种思想予以解决。所以,平时注重对数学思想的认识归纳和掌握,对于提升认识并解决问题的能力大有益处。
·编辑尹军
