基于Matlab的三维四步编织仿真
2016-08-06章宇界阎建华
章宇界,阎建华
(东华大学 a. 纺织学院;b. 研究院,上海 201620)
基于Matlab的三维四步编织仿真
章宇界a,阎建华b
(东华大学 a. 纺织学院;b. 研究院,上海 201620)
摘要:根据编织参数对四步法编织进行算法演绎,得到编织体的具体工艺参数,然后利用Matlab 编写脚本追踪携纱器的运动,确定纱线运动的空间位置趋势并存储到矩阵中,编写B均匀样条曲线脚本并在CATIA软件中导入空间纱线位置点并生成样条曲线,实现三维四步法编织的仿真以及矩形编织和圆形编织建模.以4×4矩形编织、3×18圆形编织为例,对具体编织参数展开计算,对纱线轨迹算法进行优化,实现编织预制件的仿真.
关键词:三维编纱; 纱线轨迹; 编织参数; Matlab; 仿真
三维编织是20世纪80年代兴起的新型纺织技术,不同于其他三维织物,三维编织中的纱线运动较为复杂,所有纱线按一定规律相互交织,相互之间交缠紧密,构成三维一体成型织物.直接观察三维编织物结构存在一定难度,而仿真模拟不仅提供了可视化的模型,可根据编织工艺参数变化观察织物的表观形态,还能进行有限元分析,从而得到最优参数,节约大量的时间和成本.充分利用计算机强大的图形处理功能,建立数字化的几何模型,对三维复合材料的力学结构研究具有重大意义[1].目前,常用的三维编织方法为二步法和四步法,其中四步法可以编织许多不同截面的结构.当前用四步法对矩形、圆形编织的空间纱线轨迹模拟及预制件仿真还不够全面,大部分还停留在模拟矩形编织纱线轨迹上,对可视化三维建模特别是圆形编织的研究还不够深入[1-6].本文通过Matlab软件与CATIA软件联合建模,采用B均匀样条原理实现矩形编织和圆形编织的空间纱线轨迹模拟及其预制件仿真.
1矩形编织
1.1编织参数
调整编织参数会影响织物紧密程度、纱线体积分数,进而影响织物性能,而编织参数也给产品的可设计性提供契机.一般的编织参数有表面编织角、预制件尺寸和编织纱线数等.
参照文献[2-3],对于矩形编织, 假设载纱器横向运动一步, 编织纱线运动的距离为X, 纵向运动一步, 编织纱线运动的距离为Y, 每纵向或横向运动一步后, 制件成型方向前进的节距为Z.假设编织样品宽度为W,厚度为T,行列数分别为m和n,表面编织角为α,水平角为δ,编织花节长度为h,则单胞尺寸可表示为
(1)
给定编织样品宽度W与厚度T,可得
(2)
(3)
此处的W为左边缘纱线与右边缘纱线的中心距,编织体实际宽度应该为W+d,其中d为纱线直径,如图1所示.

图1 编织体宽度Fig.1 Width of braided preform
1.2算法设计
携纱器底盘上的每个携纱器都有各自的平面位置,且携纱器的运动轨迹是连续的,故纱线的轨迹也是可追踪的.基本原理:以i、j分别表示当前某携纱器处于i排j列并记录每次运动一步后的平面位置,为便于区分,每个携纱器以数字标记序号.只要追踪每个数字所代表的携纱器,就可记录其运动位置的变化,同时设置编织速度,得到纱线的空间位置变化即纱线轨迹.以4×4矩形编织为例,需要的纱线数S为
S=m×n+m+n
(4)
故此例中纱线数S=24,其纱线排布如图2所示.

图2 4×4矩形编织携纱器排布Fig.2 Yarn carriers align of 4×4 rectangular braiding
以矩阵形式表示该携纱器初始位置如图3所示,其中0表示携纱器上无纱线,1~24分别为24个有效携纱器.

图3 携纱器初始位置矩阵
携纱器按一定规律运动,相邻两列或两排的携纱器运动方向是相反的.如图4所示,携纱器进行第一步运动时,第三、五排深色携纱器向左移动一步,第二、四排浅色携纱器向右移动一步.
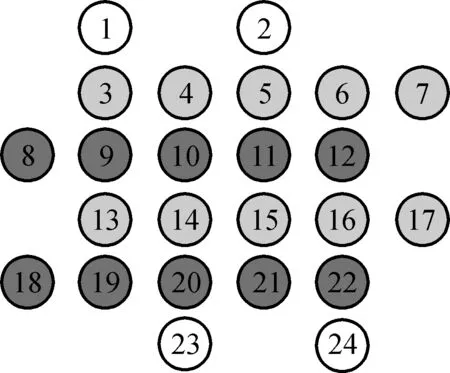
图4 携纱器第一步排布Fig.4 Align of the first step of yarn carriers
可用矩阵表示携纱器第一步位置如图5所示.

图5 携纱器第一步位置矩阵
第二步时,第二、四列携纱器向下移动一步,第三、五列携纱器向上移动一步.携纱器运动直到第四步完成一个循环,第二到第四步携纱器排布矩阵变化过程分别如图6~8所示.

图6 携纱器第二步位置矩阵

图7 携纱器第三步位置矩阵

图8 最终携纱器排布矩阵
纱线的运动轨迹数即组数G由m和n确定,计算式为
(5)
其中:LCM为两个数的最小公倍数[4].
相同运动轨迹纱线数量N可由S/G得到,以“3”携纱器为例,一个循环中其X-Y矩阵位置变化为(2,1)→(2,2)→(3,2)→(3,3)→(4,3).与“3”携纱器有相同运动轨迹的携纱器共有4个,与此运动轨迹不同的有3种,共4种运动轨迹.对纱线的运动轨迹进行归类,可简化对编织体的分析.
根据X,Y,Z的赋值,“3”携纱器上的纱线空间位置(2X,Y,0)→(2X,2Y,h/4)→(3X,2Y,h/2)→(3X,3Y,3h/4) →(4X,3Y,h).对于纱线空间位置的变化,可以用矩阵来记录.X{m}、Y{m}可表示携纱器在平面内的运动位置变化,可转化为纱线的空间位置变化矩阵M.实际上,经过上述步骤得到的是构成轨迹曲线的点的集合,需要导入建模软件中生成轨迹曲线和仿真建模.

在Matlab中创建脚本,记录各携纱器的平面位置走向,脚本如下:
form=1:S
[i,j]=find(A==m);
X{m}=[X{m}i];
Y{m}=[Y{m}j];
end
其中:A为携纱器平面位置矩阵;X{m}、Y{m}记录第m个携纱器的横向与纵向位置.将X{m}、Y{m}转化为纱线的空间位置变化,同时存储到矩阵集合中,得到24根纱线的空间位置矩阵,利用循环语句,可计算出M,用Matlab脚本可表示为
M=[];
fori=1:S
M=[M;[x1 *X{i}′,y1*Y′,z1*z′]];
end
其中:M为纱线空间运动位置点的集合矩阵;x1和y1分别代表纱线横向、纵向运动一步的步长;z1表示节距.
1.3编织体模拟
软件运行环境为Windows 7(32位),计算机CPU为双核2 GHz,计算机内存为2 GB.
令脚本运行两个编织循环,记录纱线每运动一步所处的位置并导入Excel表格中,运行时间为4.07 s, 使用CATIA的宏功能,将每条纱线的轨迹点进行插值连接,得到的纱线轨迹如图9所示.赋予这些纱线一定的截面形状,生成仿真编织体.若截面面积过大,则致使纱线之间产生穿插,如图10所示,取纱线截面为圆形,直径d为0.7mm,观察可发现,纱线的屈曲较多,编织体较为松弛且纤维体积分数较低,不太符合实际的交织运动轨迹.

图9 4×4矩形编织体纱线轨迹Fig.9 Yarn traces of 4×4 rectangular braided preform

图10 4×4矩形编织体渲染图Fig.10 Rendering figure of 4×4 rectangular braided preform
1.4算法优化
在实际编织过程中,纱线是有张力的,不会产生图9所展现出的松弛结构,由于拉力的作用及打紧作用,纱线会自动地沿着最短的路径展开,折线及松弛曲线形式的路径是不存在的,表面的纱线紧绕包缠预制体,内部纱线沿最短路线交织,故需对算法进行优化.文献[2,5]采用Bézier拟合纱线轨迹,Bézier曲线可以从多边形的形状来预测所要产生曲线的形状,可通过对多边形定点的控制来改变曲线的形状,但在Bézier曲线中任何一个控制顶点发生改变,会使得整条Bézier曲线形状发生变化.基于此,文献[7]提出了B样条曲线方法,继承了Bézier曲线优点的同时克服了上述缺点[8],其优势在于曲线可以分段,任意改变一个控制顶点只会影响相邻曲线的形状而不影响整条曲线的走向,有效解决了局部控制和连接问题.文献[6,9-10]使用B样条曲线进行拟合. 因为矩阵M中控制点的分布较为均匀,故采用三次B均匀样条曲线拟合纱线轨迹.三次B均匀样条曲线需要4个控制顶点确定三次多项式曲线,计算式为
(6)
其中:pi为控制顶点即空间坐标值点;Ni,3为节点向量.用矩阵形式可表示为
(7)
其中:u∈[0,1].三次B均匀样条曲线并不经过控制顶点,这与实际结构中纱线因相互作用而产生偏移的情况符合,故用B均匀样条曲线拟合纱线运动轨迹.如图11所示,仍取纱线直径d=0.7mm, 编织预制件经优化后变得紧凑,由其中某根纤维束的运动趋势可见纱线屈曲得到改善,仿真预制件纤维体积分数得到提升,与真实预制件更为接近.

图11 优化模型Fig.11 Optimized model
在三维编织过程中,预制件的纤维分数、纤维束的走向等主要由编织角的大小决定,编织角增加,花节长度减小,仿真模型变得更加紧凑,同时纱线张力也相应增加,使得预制件在高度方向被压缩.在实际编织中,编织角主要由打紧作用控制,打紧后编织体内部纱线的屈曲减少,使得纱线张力增大,打紧力越大,纱线间空隙减少,结构也越为紧凑,编织体不易松弛和垮塌.取W=10mm,T=6mm,m=6,n=10, α=40°,d=0.6mm,进行3个循环后其仿真模型如图12所示,运行时间为4.46s.

图12 6×10矩形编织体Fig.12 6×10 rectangular braided preform
在生成空间编织体时,需考虑编织体的整体紧密性.换言之,编织参数例如编织角的选取需要参考实际编织体结构参数,编织体应该是纱线紧密排布,编织过程中纱线间相互挤压但不穿插以保持编织体不松弛、不垮塌.同时纱线截面的选择在一定程度上也影响紧密性及编织复合材料的纤维体积分数.
2圆形编织
2.1编织参数
三维圆形编织的优势在于能够对圆形管件和异形件进行一体成型,制成的复合材料具有优异的力学性能. 当前对于圆形编织建模的研究较少,圆形编织纱线轨迹模拟和编织体建模对分析圆形编织结构、评价三维圆形编织复合材料和结构优化设计具有重要意义.
编织圆形管件的原理和矩形预制件是相通的,同样是四步法成型,而不同之处在于纵向运动改为径向运动,横向运动变为周向运动,纱线的排列方式与交织结构因此发生变化.纱线在编织体外围和内围间往复,故编织角也是动态变化的.携纱器周向和径向间歇运动带动纱线交织,管件因此成型.底盘上首列与末列相邻,故周向不再有附加纱线,径向附加纱线仍存在且只能进行径向运动.经过四步法运动后,一个机器循环完成,重复上述编织运动,纱线将相互交织而形成一定长度的管状编织体.管件的编织需要使用芯模以支撑编织体,芯模的外形也会对编织体的交织结构产生一定的影响,这里只讨论常规圆形编织.
圆形编织中,纱线数量因周向不再有附加纱线,故纱线数计算方式变为:S=(m+1)n,其中n为列数且必须为偶数,否则必有相邻两列携纱器运动轨迹相同.纱线运动轨迹数即组数G[11]为
(8)
编织角α是一个重要的编织工艺参数,预制件表面形成的交织纹路角称为编织角,其正切等于预制体表面的花节宽度与花节长度之比.假设某管件的内外径为din、dout,第i列最外部纱线在一个循环之后会移动到相邻列,所走过的曲线平面投影为一圆弧,圆弧长度为2πdout/n,同理,最内部某纱线在一个循环后所走过的平面圆弧长度为2πdin/n.故由内外编织角的定义可知:
(9)

2.2算法设计
以3×18管件编织为例,假定din=12 mm,dout=24 mm,αout=40°,则需要的纱线数量为S=72,纱线组数G=108/18=6,相同运动轨迹携纱器数量N=S/G=12,其携纱器排布如图13所示,共有6种图案分别代表6组携纱器,相同图案代表具有相同运动轨迹的携纱器.相邻列携纱器的夹角定义为θ0=360°/n,以[i,j]表示某携纱器运动若干步后处于第i层和第j列,以r、θ表示该携纱器上纱线中心与管件中心连线距离以及该连线与垂直方向的夹角,利用三角函数运算得到其面内位置.
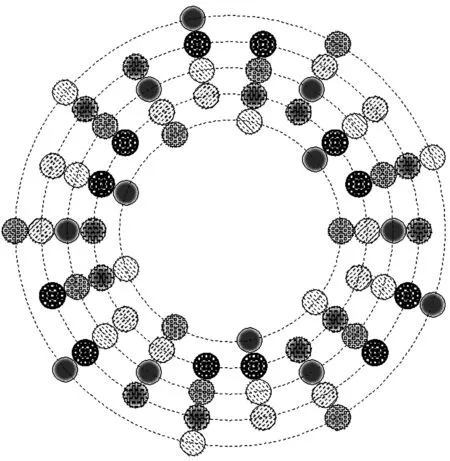
图13 3×18圆形编织携纱器分布Fig.13 Yarn carriers align of 3×18 tubular braiding
在Matlab中运行创建的脚本文件,读取携纱器初始位置和每一步之后的平面位置,并转化为每根纱线的实际空间位置变化并记录存储,Matlab脚本如下:
form=1:S
[i,j]=find(A==m);
θ=(j-1)*θ0;
r=(a+2-i)*D+din/2;
x=r*sinθ;
y=r*cosθ;
X{m}=[X{m}x];
Y{m}=[Y{m}y];
end
其中:a为排数;相邻层同列纱线的中心距D= (dout-din)/2(m+1),X{m}、Y{m}记录第m条纱线的周向与径向位置及其变化.
在Matlab脚本程序中输入编织参数m、n、din、dout、αout的值,得到72根纱线的空间轨迹变化集合矩阵.对该矩阵同样进行B均匀样条曲线拟合后的 纱线轨迹如图14所示,取纱线直径d=1.5 mm,仿真效果如图15所示,运行时间为4.24 s.

图14 3×18管件编织体纱线轨迹Fig.14 Yarn traces of 3×18 tubular braided preform
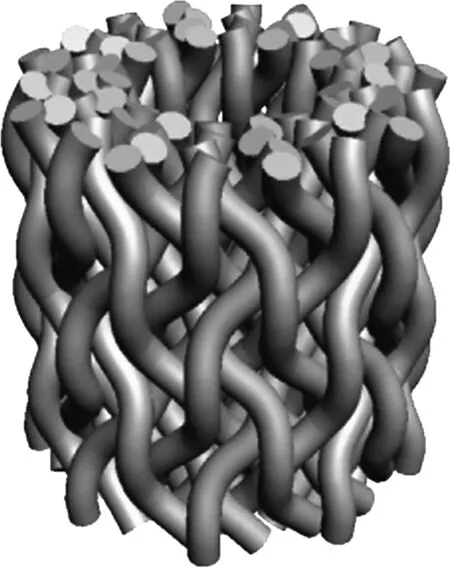
图15 3×18管件编织体仿真Fig.15 Simulation of 3×18 tubular braided preform
取6×36管件编织进行仿真,假定din=12mm,dout=24mm,αout=30°,纱线共计252根,取纱线直径d=0.8mm,运行3个循环,仿真编织预制件如图16所示,运行时间为6.63s.

图16 6×36管件编织体仿真Fig.16 Simulation of 6×36 tubular braided preform
实际上,纱线之间存在相互挤压,挤压处截面会产生变形,而非规则的圆形,而且预制件在经过固化成型工艺成为复合材料后,由于与树脂的相互作用,纱线变形进一步加大,这与仿真结果是有差异的.另外为了避免纱线的穿插,所取纱线直径均较小,以致仿真预制件的纤维体积分数较低,希望在今后的算法研究中得到改善.
3结语
本文以三维矩形编织和圆形编织为例,利用Matlab记录纱线的空间运动变化,并用B均匀样条曲线拟合纱线轨迹重新生成轨迹点,导入CATIA软件以实现四步法矩形和圆形编织预制件中纱线轨迹的模拟与预制件的仿真,并对关键算法进行说明.使用B均匀样条曲线进行纱线轨迹拟合与编织预制件仿真,基本接近真实编织效果,同时矩形编织和圆形编织中纱线间的穿插效果也得到改善.
通过输入编织工艺参数,实现计算机编织模拟,用户可以进行编织参数的调整,直观地了解产品的基本外观以及纱线的空间走向并实时调整,在一定程度上实现可视化.
参考文献
[1] 肖来元,汪博峰.三维编织复合材料几何成型算法及仿真研究[J].计算机工程与科学,2008,30(1):82-85.
[2] 邵将,温卫东,崔海涛.三维四步法编织复合材料结构的计算机仿真[J].南京航天航空大学学报,2009,41(1):36-40.
[3] CHEN L, TAO X M, CHOY C L. On the micro structure of three-dimensional braided preforms [J]. Compos Sci Technol, 1999,59(3):2383-2391.
[4] 陈利,李嘉禄,李学明.三维编织中纱线的运动规律分析[J].复合材料学报,2002,19(2):71-74.
[5] 周新贵,张长瑞,龚国辉,等.三维编织物的真三维仿真[C]//2000年中国材料研讨会论文集.2000:4.
[6] 何红闯,杨连贺,陈利.矩阵组合截面四步法二次三维编织及其空间模型可视化[J].复合材料学报,2010,27(4):160-167.
[7] 张明星.广义Bézier曲线与B样条曲线的研究[D].长沙:中南大学数学与统计学院,2013.
[8] 肖来元,寇晓菲. 三维编织复合材料编织工艺过程仿真研究[J]. 计算机工程与科学,2014,36(4):719-724.
[9] KANG T J, KIM S J, JUNG K. Analysis of geometrical parameters using a CAD system for a 3-D braided preform [J]. Textile Research Journal, 2008,78(10): 922-935.
[10] BARSKY B A, BEAUTY J C. Local control of bias and tension in beta-splines [J]. ACM Trans on Graphics, 1983,2(2):109-134.
[11] 曹红蓓,王君泽,瞿畅,等.管状三维编织物三维动画仿真探索[J].纺织学报,2004,25(5): 71-73.
文章编号:1671-0444(2016)03-0363-07
收稿日期:2015-04-28
基金项目:上海市科委资助项目 (12521102400)
作者简介:章宇界(1990—),男,浙江嘉兴人,硕士研究生,研究方向为纺织复合材料. E-mail:zhangyujie181@sina.com 阎建华(联系人),男,研究员,E-mail:jh_yan@dhu.edu.cn
中图分类号:TB 332
文献标志码:A
Simulation of Four-Step Three-Dimensional Braiding Based on Matlab
ZHANGYu-jiea,YANJian-huab
(a. College of Textiles; b. Research Institute, Donghua University, Shanghai 201620, China)
Abstract:The parameters of braiding preform is obtained by an algorithm deduction according to four-step three-dimensional (3-D) braiding parameters. The traces of yarn carriers can be acquired by a Matlab script. Through such a way, the space position trends of yarn movements are gained and can be stored into a matrix for four-step braiding. A script of uniform rational B-spline is compiled to generate points data of yarns and then plot into splines in CATIA software. By means of that, the simulation and modelling of four-step 3-D braiding are realized. 4×4 rectangular braiding and 3×18 tubular braiding are quoted as examples to simulate braiding preforms through calculation of specific braiding parameters and optimization of the algorithm for yarn traces.
Key words:three-dimensional braiding; yarn trace; braiding parameters; Matlab; simulation
